解答含参不等式恒成立问题的几种思路

尹尧

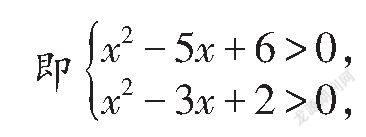
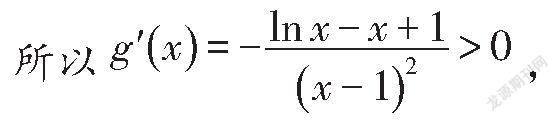
含参不等式恒成立问题一般较为复杂.仅运用不等式的性质，往往很难找到使不等式恒成立的条件，使问题顺利得解.这就需要采用不同思路，如变换主元、分离参数、分类讨论等来解题.下面结合实例来谈一谈解答含参不等式恒成立问题的三种思路.

一、变换主元

变换主元法是指将问题中主元、参数的位置互换，即将参数视为主元，将主元视为参数进行求解的方法.运用变更主元法解答含参不等式恒成立问题，需先找出所要求证不等式中的变量与参数，然后将两者进行互换，得到新不等式，根据新主元的取值或者限制条件，列出满足题意的不等式或不等式组，从而解题.

例1，对于任意-1≤a≤1，x+（a-4）x+（4-2a）>0恒成立，则x的取值范围为________.

解：设f（a）=（x-2）a+（x-4x+4），a∈[-1，1]，

则问题等价于在a∈[1，1]时，f（a）>0恒成立，

解得x<1或x>3，

所以实数x的取值范围为（-∞，l）∪（3，+∞）.

将x和a进行变换，把a看作主元，构造关于a的函数f（a），便可采用变更主元法来解题.很显然f（a）为一次函数，根据一次函数的性质，要使f（a）>0恒成立，只需使[-1，l]上的所有函数值都大于0，建立关于x的不等式组，即可解题.

二、分离参数

分离参数法是解答含参不等式恒成立问题的重要方法.运用分离参数法求解不等式恒成立问题，需先将不等式进行变形，使参数分离，得到形如a≤f（x）、a<f（x）、a>f（x）、a≥f（x）的式子，只要使a≤f（x）、a<f（x）、a>f（x）、a≥f（x），就能确保不等式恒成立.在求f（x）的最值时，往往可根据导数的性质、函数的单调性，或利用基本不等式.

例2.已知函数f（x）=-xlnx+a（x+1），若f（x）≤2a在[2，+∞）上恒成立，求a的取值范围.

令t（x）=lnx-x+1，x≥2，

当x≥2时，t′（x）<0，

故t（x）在[2，+∞）上單调递减，

可得t（x）=ln2-l<0，

则函数g（x）在[2，+∞）上单调递增，

可得a≤g（x）=g（2）=2ln2，

所以a的取值范围为（-∞，2ln2].

首先将不等式进行移项、变形，使参数a分离，得到a≤g（x）对函数g（x）求导，根据导函数与函数的单调性之间的关系判断出函数g（x）的单调性，求得函数g（x），即可运用分离参数法，确定参数a的取值范围.

三、分类讨论

含参不等式恒成立问题中参数的取值往往不确定，因而在求解含参不等式恒成立问题时，需灵活运用分类讨论法，对参数或某些变量进行分类讨论，从而求得问题的答案.而确定分类讨论的标准是解题的关键，可根据一元二次方程的判别式大于、等于、小于0进行分类讨论;也可根据二次函数的二次项系数大于、小于。进行分类讨论;还可根据导函数值大于、等于、小于0进行分类讨论.

例3.设f（x）=x-2mx+2，当x∈[-l，+∞）时，f（x）≥m恒成立，求参数m的取值范围.

分析：首先将不等式f（x）≥m转化为F（x）=x-2mx+2-m≥0.要使F（x）≥0，需使该函数在x∈[-1，+∞）上恒大于或等于0.由于x-2mx+2-m=0为一元二次方程，只需讨论方程在x∈[-1，+∞）上的根的分布情况.而方程的根的分布情况主要由判别式确定，所以需采用分类讨论法，对方程的判别式与0之间的大小关系进行讨论.

解：设F（x）=x2mx+2-m，

则问题等价于当x∈[-1，+∞）时，F（x）≥0恒成立，

①当Δ=4（m-1）（m+2）<0，即-2<m<1时，F（x）>0恒成立，

解得-3≤m≤-2，

综上所述，参数m的取值范围为m∈[-3，1）.

采用分类讨论的思路来求解含参不等式恒成立问题，一般可将参数或与参数相关的量定为分类讨论的对象，再根据题意确定分类讨论的标准，逐层、逐级进行讨论，最后综合所得的结果即可.

相比较而言，第一种思路的适用范围较窄;第二、三种思路较为常用，但第三种思路解题的过程繁琐，且运算量较大.因此在解题时，同学们可首先尝试将参数分离，将问题转化为最值问题来求解;若行不通，再考虑运用变更主元、分类讨论的思路.