高考数学模拟试题（八）

黎若青

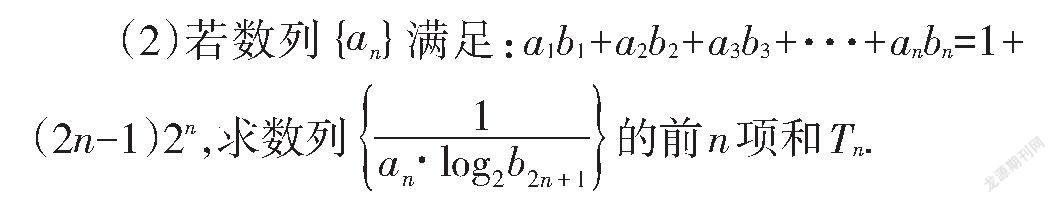
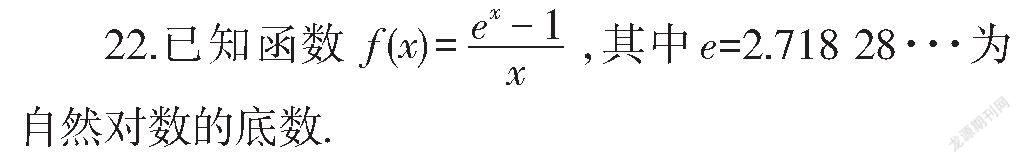
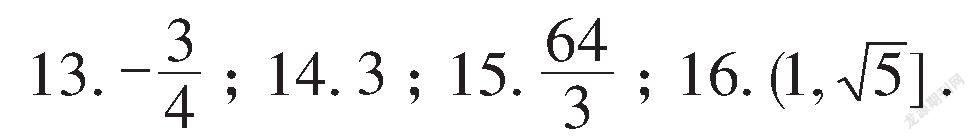
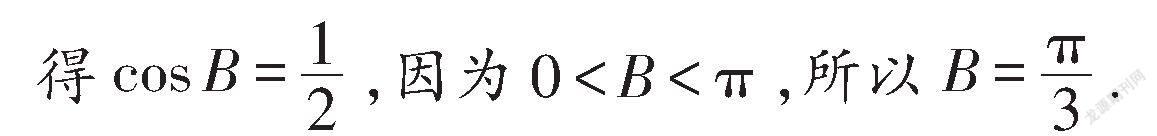
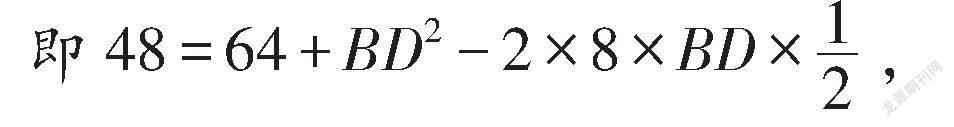
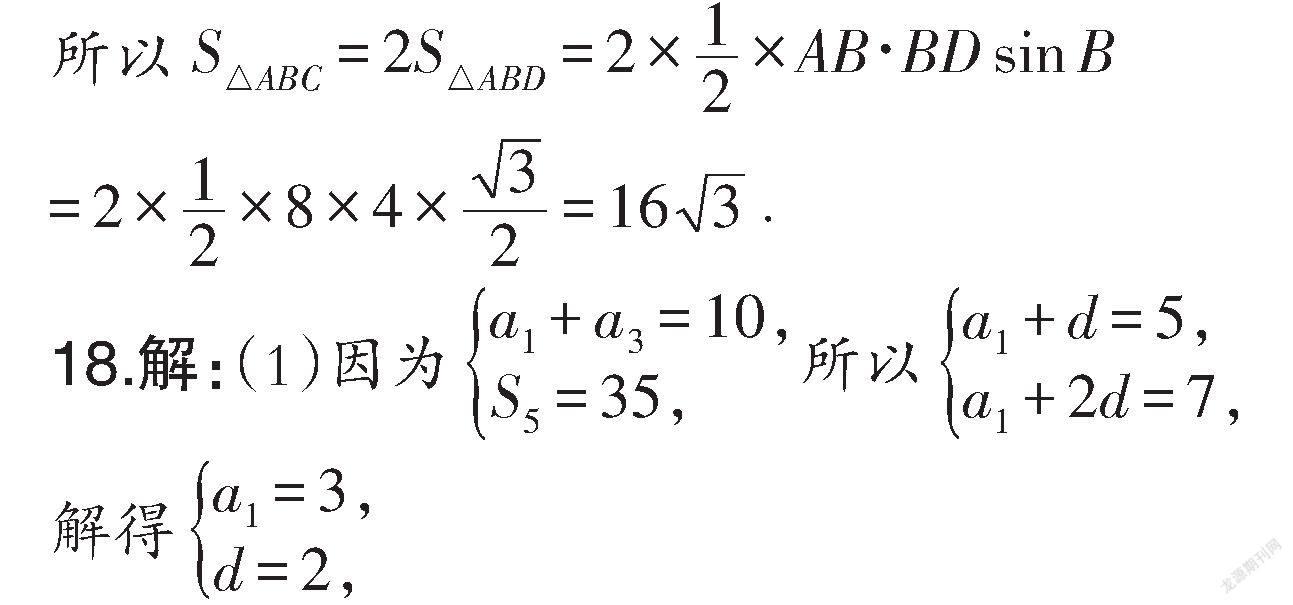
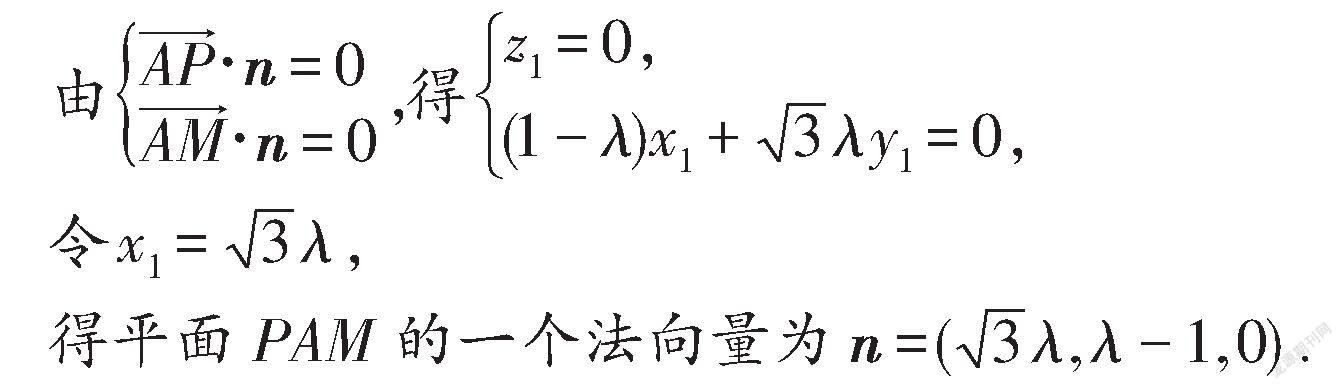
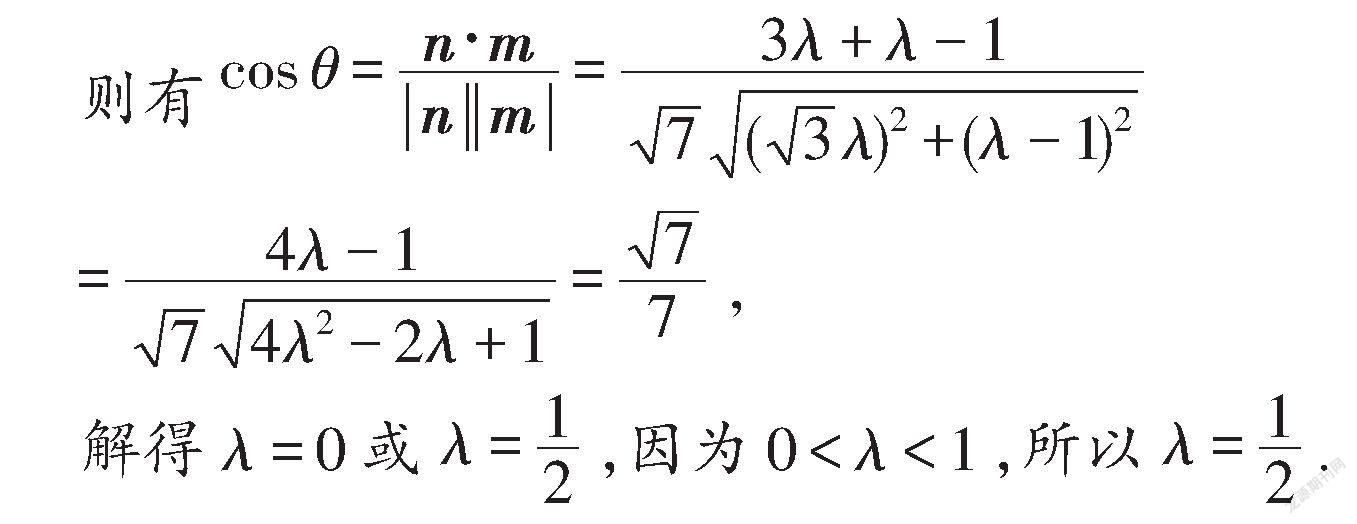
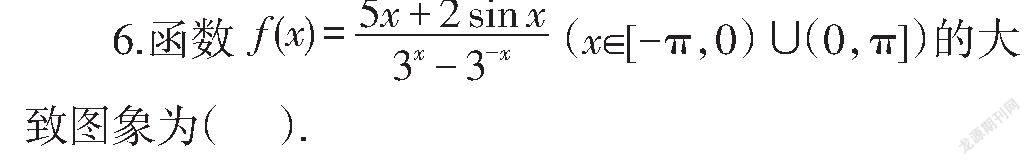
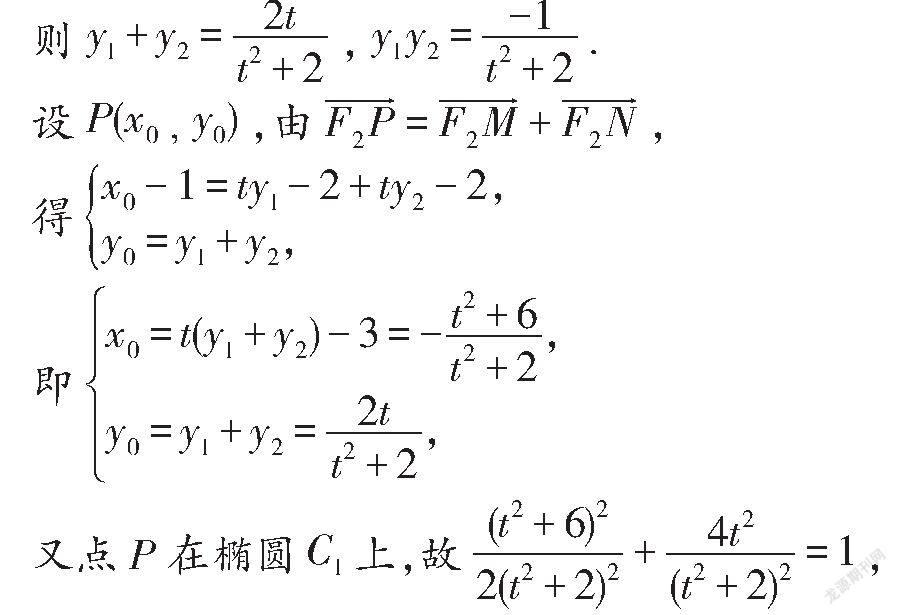
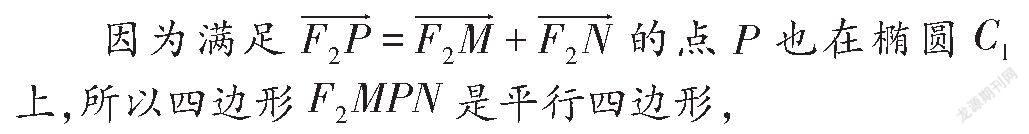
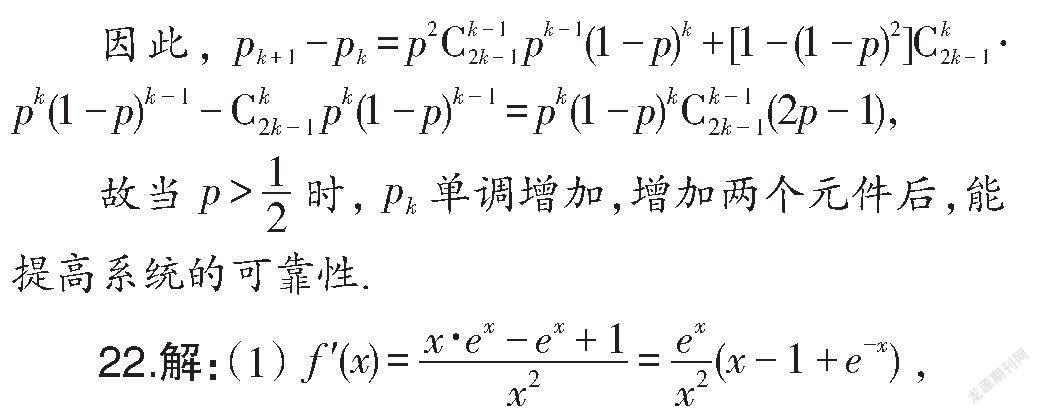
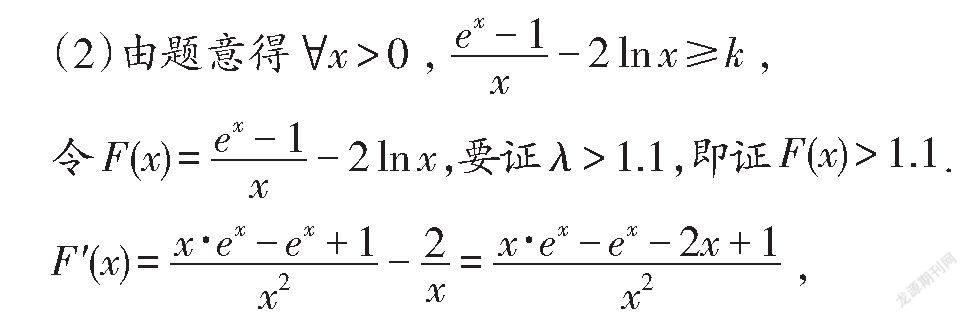
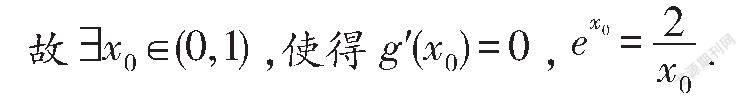
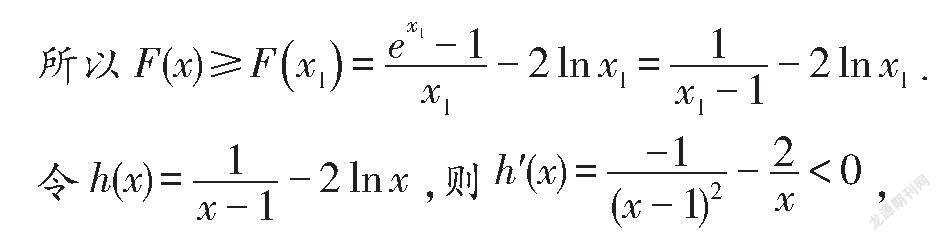
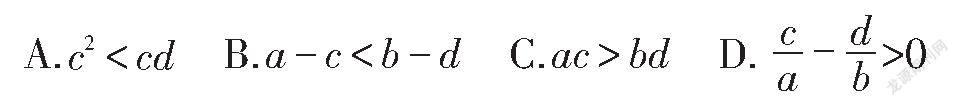
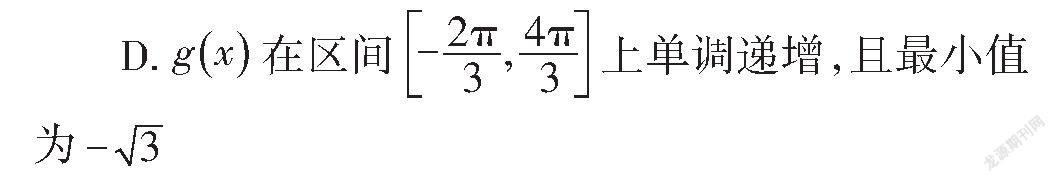
一、单项选择题

A.（-2，4）  B.（l，2）     C.（l，4）     D.（2，4）

2.设i·z=4-3i（i为虚数单位），则复数z的虚部为（）

A.-4 B.4  C.-4i       D.4i

3.已知等比数列{a}中，a=4，aa=8a，则a=（）.

A.1  B.2  C.±1 D.±2

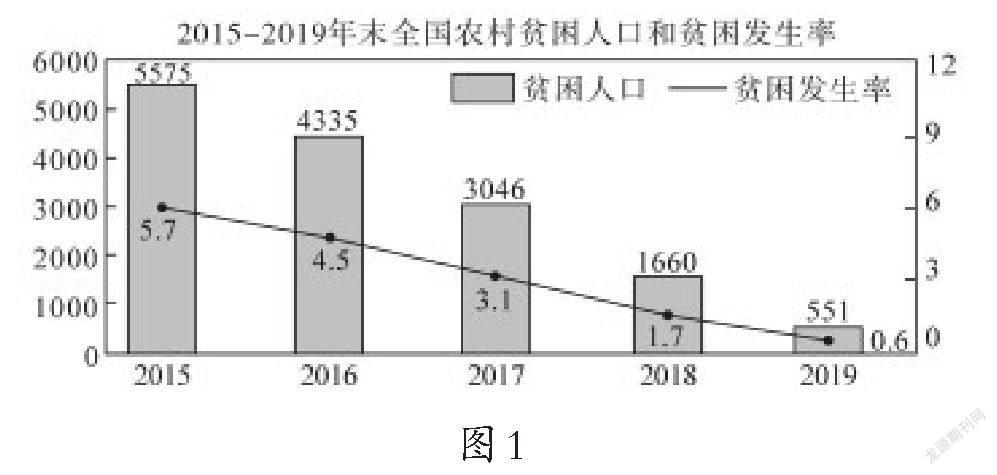
4.2020年，我国脱贫攻坚已取得决定性胜利，下图是2015-2019年年末全国农村贫困人口和贫困发生率（贫困人口占目标调查人口的比重）的變化情况（数据来源：国家统计局2019年统计年报）.根据图1可得出的正确统计结论是（）.

A.五年来贫困发生率下降了5.2个百分点

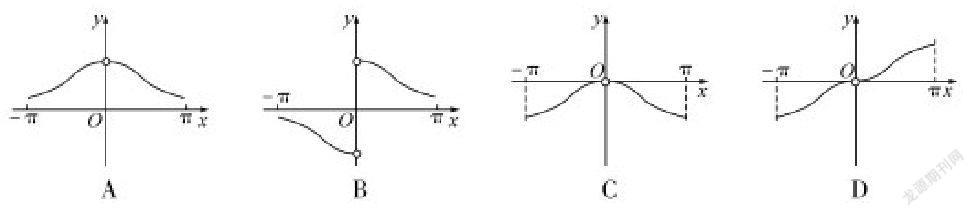
B.五年来农村贫困人口减少超过九成

C.五年来农村贫困人口减少得越来越快

D.五年来目标调查人口逐年减少

5.已知圆M过点A（1，-1），B（1，2），C（5，2），则圆M在点B处的切线方程为（）.

A.3x+4y-2=0  B.3x-4y-2=0

C.4x-3y+2=0  D.4x-3y-2=0

7.面对全球蔓延的疫情，疫苗是控制传染的最有力技术手段.科研攻关组第一时间把疫苗研发作为重中之重，对灭活疫苗、重组蛋白疫苗、腺病毒载体疫

苗、减毒流感病毒载体疫苗和核酸疫苗5个技术路线并行研发，组织了12个优势团队进行联合攻关.其中有5个团队已经依据各自的研究优势分别选择了灭活疫苗、重组蛋白疫苗、腺病毒载体疫苗、减毒流感病毒载体疫苗和核酸疫苗这5个技术路线，其余团队作为辅助技术支持进驻这5个技术路线.若保障每个技术路线至少有两个研究团队，则不同的分配方案的种数为（）.

A.14700  B.16800  C.27300  D.50400

8.已知函数f（x）是定义在区间（0，+∞）上的可导函数，满足f（x）>0，且f′（x）+f′（x）<0（f′（x）是f（x）的导函数），若0<a<1<b且ab=1，则下列不等式一定成立的是（）.

A.f（a）>（a+1）f（b）     B.f（b）>（1-a）f（a）

C.af（a）>bf（b）       D.af（b）>bf（a）

二、多项选择题

9.设a，b，c，d为实数，且a>b>0>c>d，则下列不等式正确的是（）.

10.将函数f（x）=2cosx图象上所有点的横坐标伸长到原来的2倍，纵坐标不变，再将得到的图象向左平移π个单位长度，得到函数g（x）的图象，则下列说法正确的有（）.

A.g（x）为奇函数

B.g（x）的周期为4π

C.∀x∈R，都有g（x+π）=g（π-x）

11.已知抛物线Γ：x=4y的焦点为F，过F与y轴垂直的直线交抛物线Γ于两点，则下列说法正确的是（）.

A.点F的坐标为（1，0）

B.抛物线Γ的准线方程为y=-l

C.线段MN的长为4

D.直线y=x-2与抛物线Γ相切

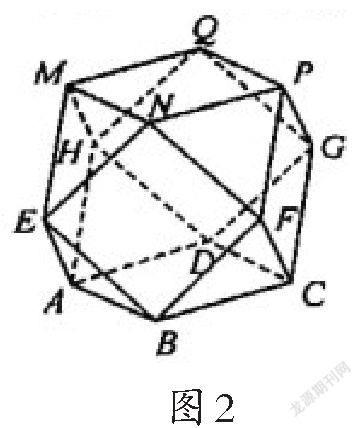
12.半正多面体（semiregular solid）亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，体现了数学的对称美.二十四等边体就是一种半正

A.BF⊥平面EAB

C.该二十四等边体外接球的表面积为8π

三、填空题

四、解答题

17.在△ABC中，角A，B，C所对的边分别是a，b，c，且4cos（A+C）+2cos2B+3=0.

（1）求角B;

18.已知等差数列{a}，其前n项和为S，若a+a=10，S=35.

（1）求数列{a}的通项公式;

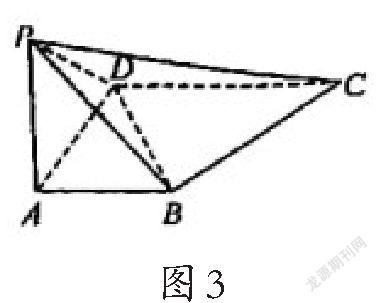
19.如图3，四棱锥P-ABCD中，底面ABCD是直角梯形，AB∥DC，∠BAD=90°，PD=DC=BC=2PA=2AB=2，PD⊥DC.

（1）求证：PA⊥平面ABCD;

（1）求椭圆C的方程;

21.某电子公司新开发一电子产品，该电子产品的一个系统G有2n-1个电子元件组成，各个电子元件能正常工作的概率均为p，且每个电子元件能否正常工作相互独立.若系统中有超过一半的电子元件正常工作，则系统G可以正常工作，否则就需维修.

（2）为提高系统G正常工作的概率，在系统内增加两个功能完全一样的电子元件，每个新元件正常工作的概率均为p，且新增元件后有超过一半的电子元件正常工作，则系统C可以正常工作，问p满足什么条件时，可以提高整个系统G的正常工作概率？

（1）求f（x）的单调区间;

（2）若e-2xlnx-kx-1≥0对∀x>0怛成立，记k=λ，证明：λ>1.1.

参考答案与解析

一、单项选择题

1-8  DDBBC  ABC

二、多项选择题

9.AD;10.ABC;11.BC;12.BCD

三、填空题

四、解答题

17.解：（1）因为A+B+C=π，

所以A+C=π-B，由4cos（A+C）+2cos2B+3=0，

可得-4cosB+2（2cosB-1）+3=0，

即4cosB-4cosB+1=0，

（2）在△ABD中，由余弦定理可得AD=AB+BD- 2AB·BDcosB，

即BD-8BD+16=0，解得BD=4.

所以a=a+（n-1）d=2n+1.

（2）由（1）得：3b+5b+7b+…+（2n+1）b

=1+（2n-1）2，①

所以3b+5b+7b+…+（2n-1））b

=l+（2n-3）2（n≥2），②

兩式相减得：（2n+1）b=（2n+1）2（n≥2），

所以b2（n≥2），

又由①式得b=1，适合上式，所以b=2（n∈N）.

19.解：（1）因为ABCD是直角梯形，AB∥DC，∠BAD=90°，所以AD⊥DC，

又因为PD⊥DC，PD∩AD=D，所以CD⊥平面PAD，

所以PA+AD=PD，所以PA⊥AD，

又AD∩CD=D，所以PA⊥平面ABCD.

设平面PBD的法向量m=（x，y，z），

设平面PAM的法向量n=（x，y，z），

设二面角A-PM-B的平面角为θ，

20.解：（1）椭圆的左右焦点分别为F（-c，O），F（c，0），

又椭圆的上顶点为（0，b），

（2）设直线l的方程为x=ty-1，代入x+2y=2，并整理得（t+2）x-2ty-1=0，

△=4t+4（t+2）>0，设M（ty-1，y），N（ty-1，y），

即t-12t-28=0，解得t=14（舍负），

设四边形FMPN的面积为S，

∴ξ的的分布列为

在2k-1个元件组成的系统中增加两个元件得到2k+1个元件组成的系统，则新系统正常工作可分为下列情形：

易证当x≠0时，e>x+1，

则e>-x+1，即e+x-1>0，

所以f′（x）>0，故f（x）在（-∞，0），（0，+∞）上单调递增.

令g（x）=x·e-e-2x+1，

则g′（x）=x·e-2，g″（x）=（x+1）·e>0，

所以g′（x）在（0，+∞）上单调递增，

又g′（0）=-2<0，g′（1）=e-2>0，