《数学通报》问题2562的一个推广

庞良绪

(上海市市西中学 200040)

1 引言

《数学通报》2020年第9期问题2562提出了一个不等式如下：

问题2562[1]设a,b,c>0，且a+b+c=3，证明：

(1)

《数学通报》2020年第10期刊登了问题提供者给出的一种证明，[2]文[3]给出了(1)式的另一种证明.

本文从项数与指数出发，给出(1)式的一个推广.

(2)

2 二个引理

为证明(2)式，先给出二个引理.

引理1(Cauchy不等式)[4]设xi，yi(i=1,2,…,n)是实数，则有

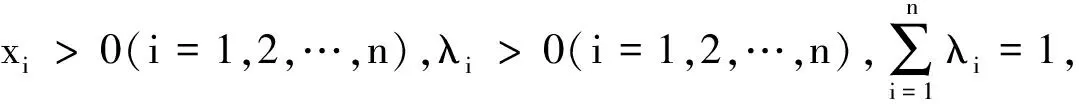
等号当且仅当x1=x2=…=xn时成立.

3 结论的证明

证明由引理1知，yi(i=1,2,…,n)是正实数，有

(3)

等号当且仅当y1=y2=…=yn时成立.

(利用(3)式)

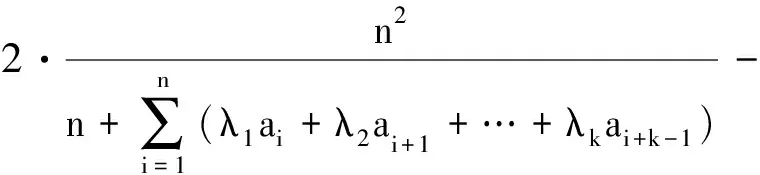
(利用引理2)

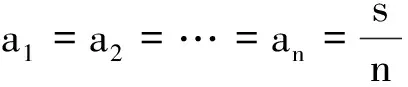
4 讨论

在本文定理中，取s=n，得

(4)

在推论1中，取n=3,k=2，则(4)变成(1)式，所以，(2)式是(1)的推广.

推论2设a,b,c>0，且a+b+c=3，则有

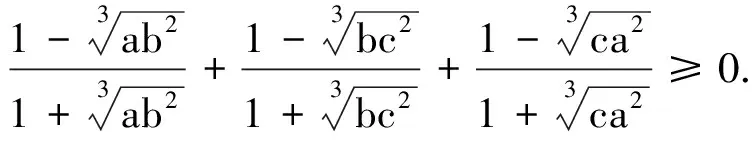
推论3设a,b,c,d>0，且a+b+c+d=4，则有