西方早期几何教科书中的圆面积公式
狄 迈 汪晓勤
(华东师范大学教师教育学院 200062)
1 引言
圆面积是历史最悠久的数学课题之一,在古代东西方不同文明的数学文献中都有记载.公元前3世纪,古希腊数学家欧几里得(Euclid)用穷竭法证明了圆面积之比等于直径平方之比;阿基米德(Archimedes, 前287-前212)利用穷竭法证明了圆面积等于直角边长分别等于圆周长和半径的直角三角形的面积.公元3世纪,中国数学家刘徽利用割圆术证明了圆面积等于半周与半径之积.17世纪,德国数学家开普勒(J.Kepler, 1571—1630)利用无穷小方法,将圆转化为直角边长分别等于周长和半径的直角三角形[1].微积分诞生后,人们采用极限的方法来求圆面积.
《义务教育数学课程标准(2011年版)》指出,要求学生通过操作,探索并掌握“圆面积”公式,并能解决简单的实际问题.现行六年级数学教科书中,人教版与沪教版将圆分割成小扇形,通过等积变形拼成近似平行四边形来推导圆面积,北师大版除了平行四边形的拼接,还介绍了多边形逼近、同心圆堆积等方法.但考虑到学生的认知基础,教科书无法采用严谨的极限方法,学生往往误以为圆面积公式只是个近似公式;而在大学微积分教学中,教师往往又因为简单而忽略了该公式.如何在“近似”与“精确”之间架设一座桥梁,是今日教学的难点.
鉴于此,本文聚焦圆面积公式的推导与证明,对西方早期几何教科书进行考察,以期为今日数学教学提供思想启迪.
2 早期教科书的选取
本文从有关数据库中选取120种西方早期几何教科书为研究对象,出版时间分布情况如图 1 所示.其中,对于同一作者再版的教科书,若内容无显著变化,则选择最早的版本,若内容有显著变化,则将其视为不同的教科书.
120种几何教科书中,圆面积主要位于“正多边形”、“正多边形与圆”、“圆”、“面积”、“度量”等章节.其中圆面积大多归于“正多边形与圆”一章之中,可见早期教科书多利用正多边形这一直边图形去研究圆.

图1 120种几何教科书的时间分布
3 圆面积公式的证明
在120种几何教科书中,关于圆面积公式的推导或证明方法可分为穷竭法、类比法、等积变形法、极限法四类.
3.1 穷竭法
9种教科书采用了古希腊的穷竭法.17世纪法国数学家巴蒂(I. G. Pardies,1636—1673)在其《几何基础》中首先证明正多边形面积为以周长为底、边心距为高的直角三角形面积,然后用穷竭法证明圆面积等于直角边长分别等于圆周长和半径的直角三角形的面积[2].
苏格兰数学家普莱费尔(J. Playfair,1748—1819)在《几何基础》(1795)中利用穷竭法证明[3]了
定理1:对于一个给定的圆,可以找到两个相似的内接与外切正多边形,使其面积与圆面积之差任意小.
定理2:若图形B的面积大于圆A的任一内接正多边形的面积,并且小于圆A的任一外切正多边形的面积,则B的面积等于圆A的面积.
然后证明了
定理3:圆的面积等于以圆周长为底、半径为高的直角三角形的面积.
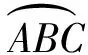
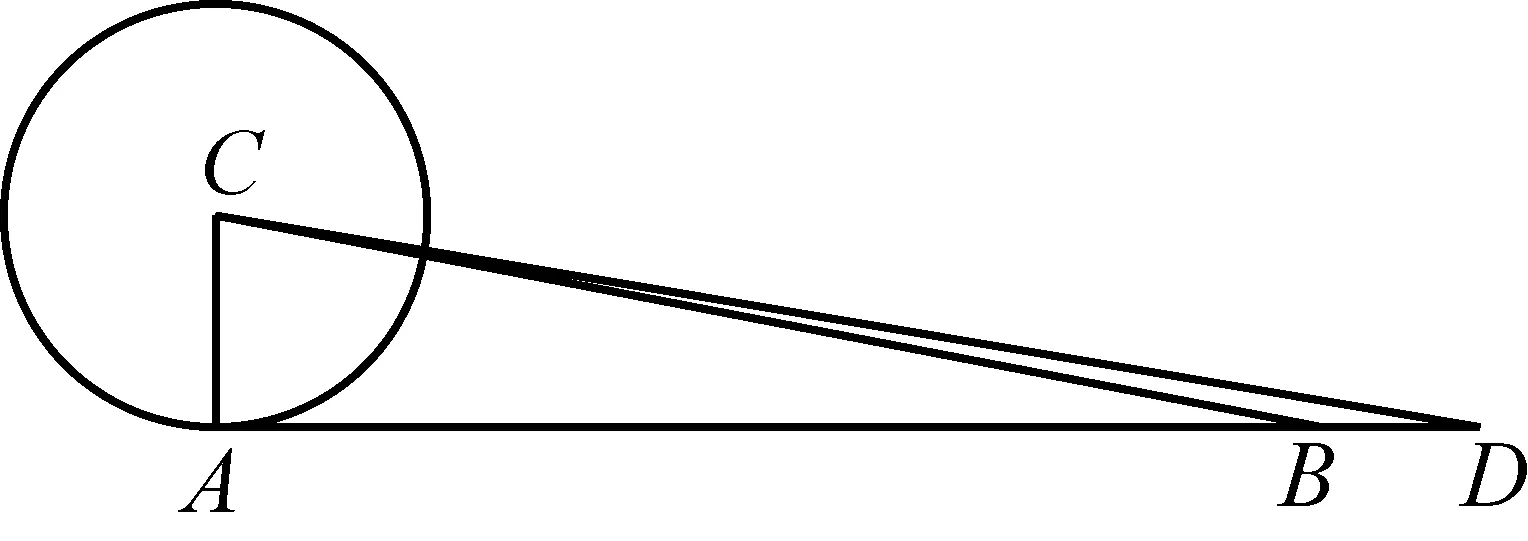
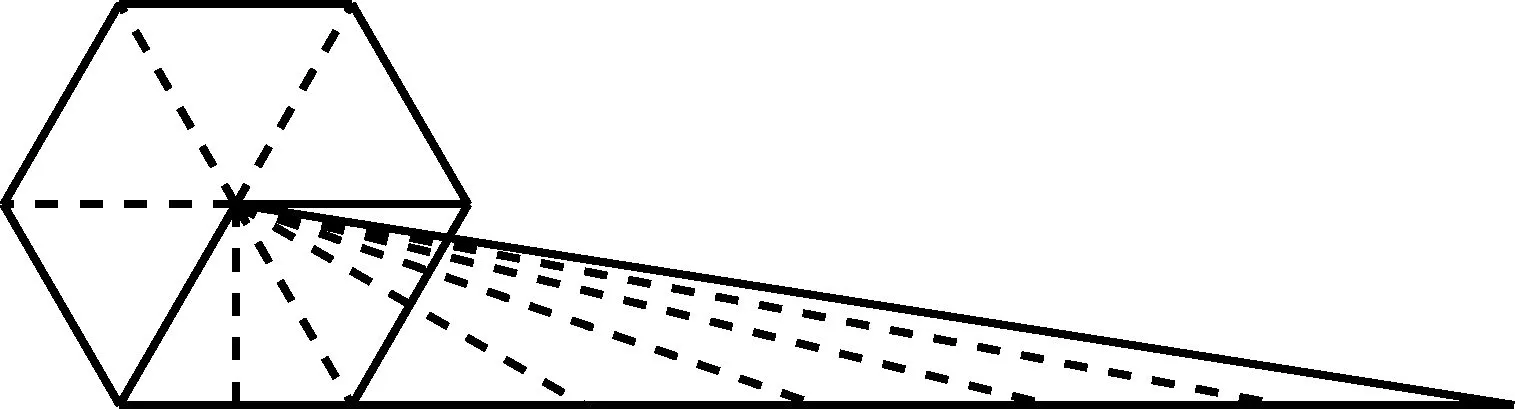
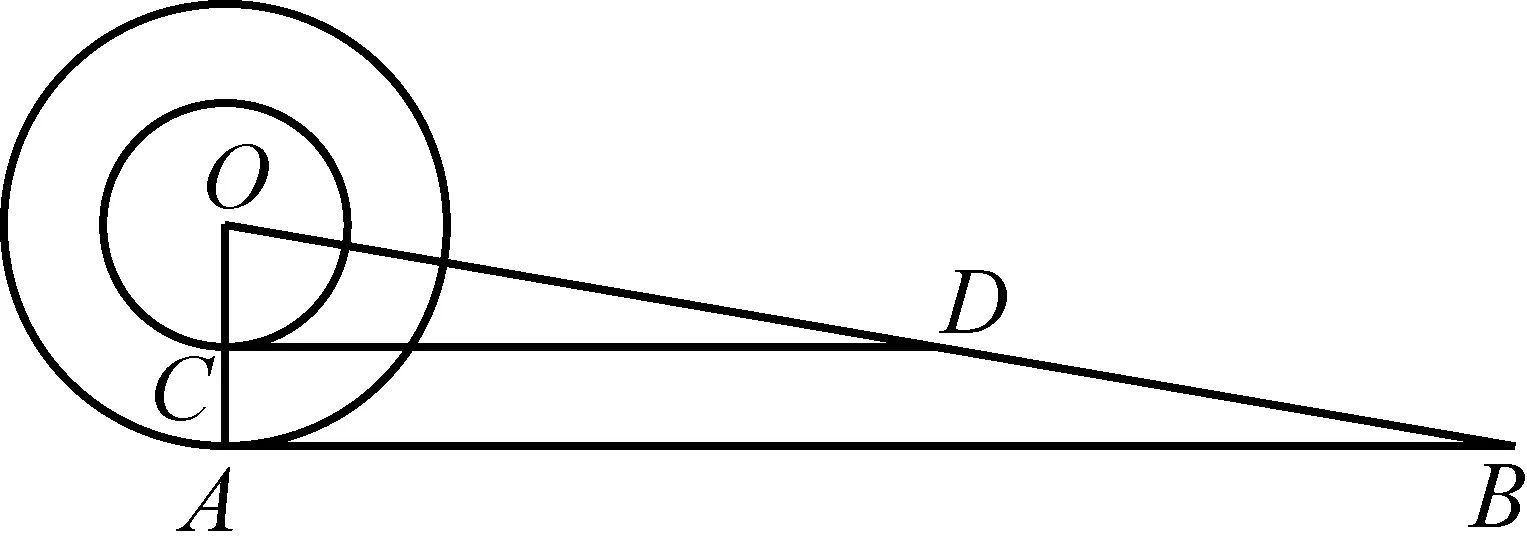
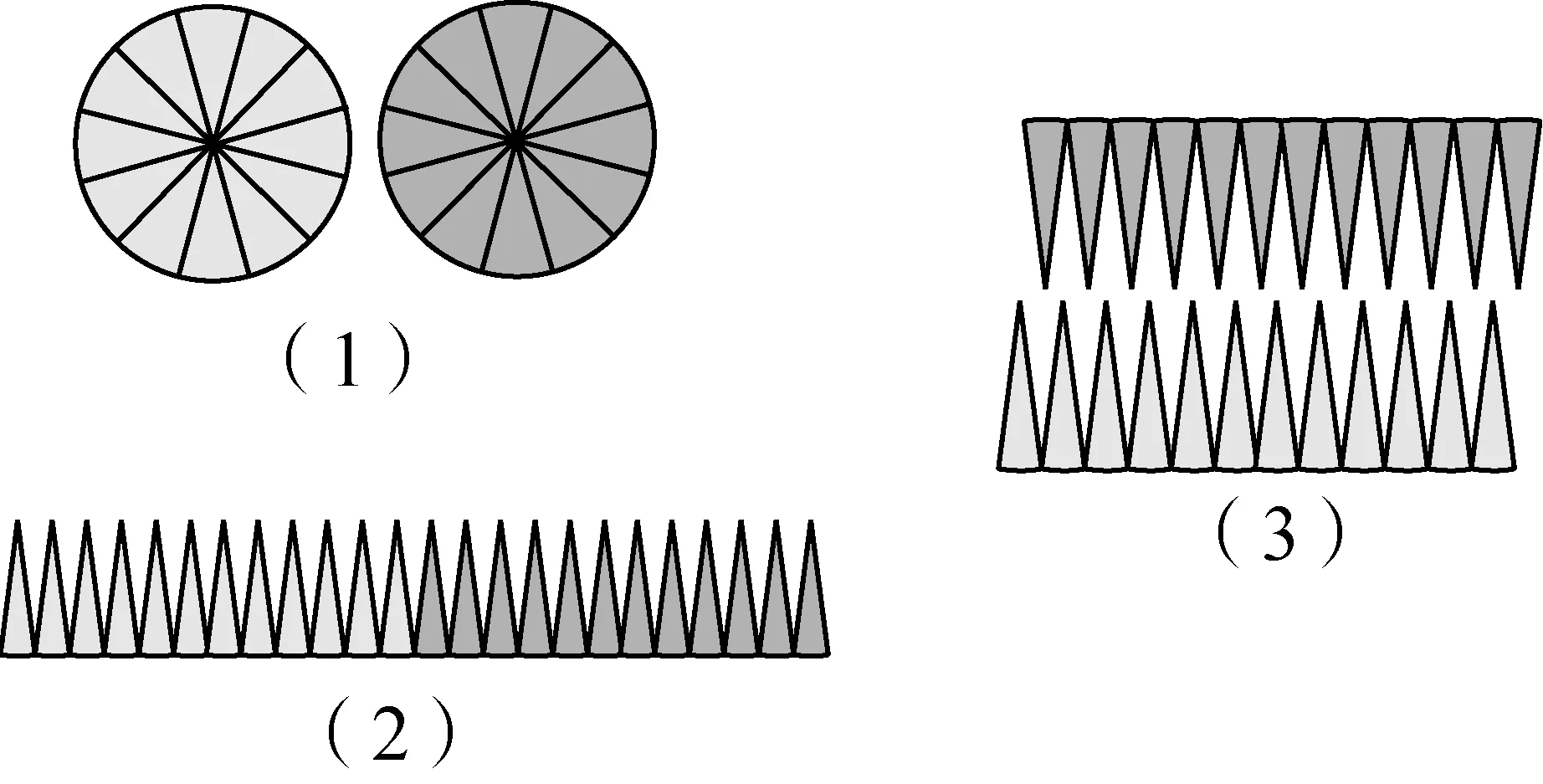
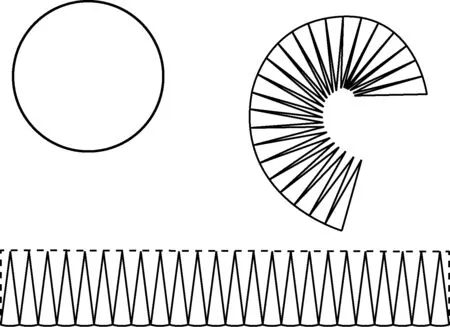
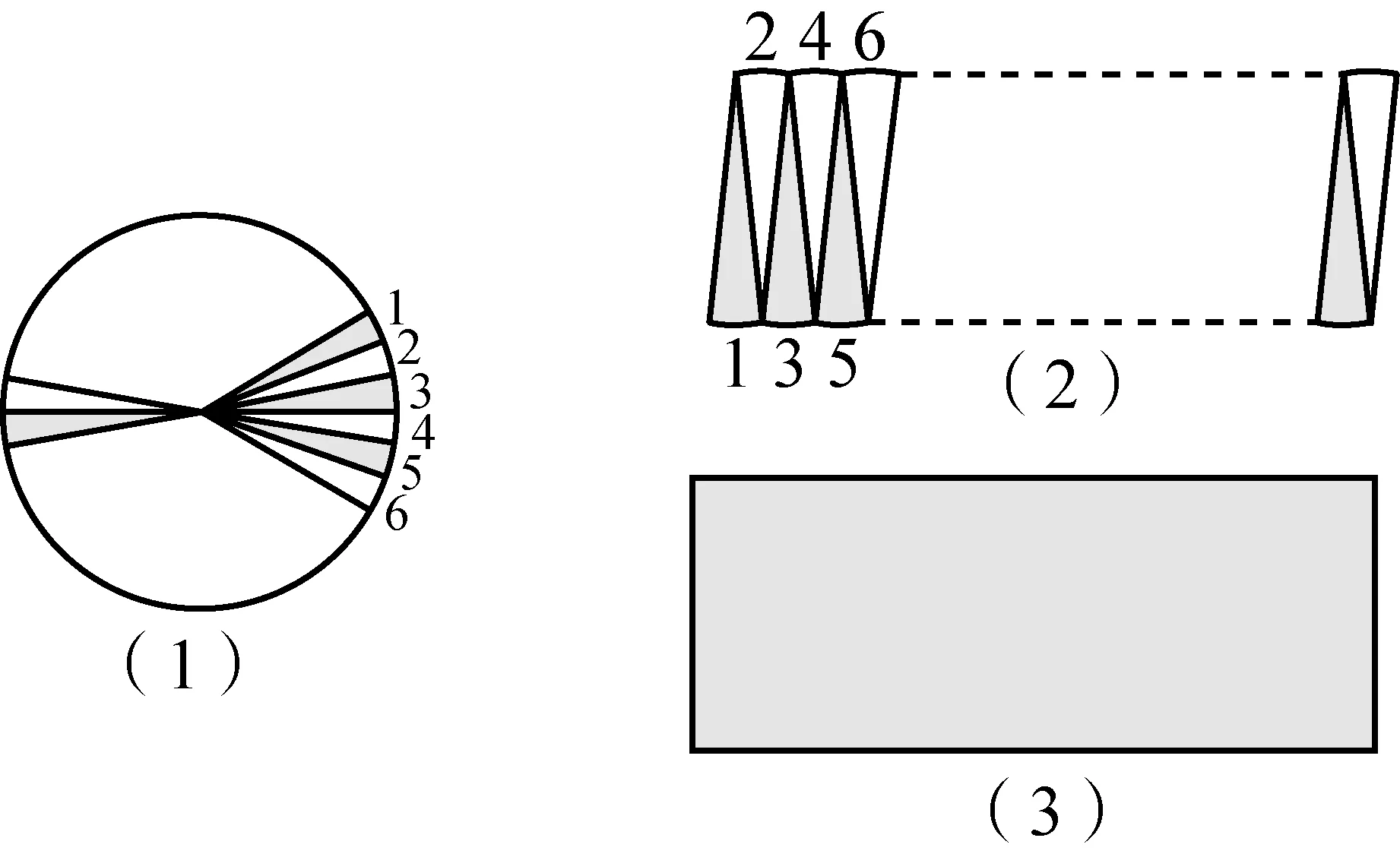
延长AC至点K和L,使AK与AL分别等于以弦AB与切线段EF为边的内接、外切正多边形的半周长,AK 图2 普莱费尔对圆面积公式的证明 图3 Morton(1830)对圆面积公式的证明 由于古希腊数学家不接受实无穷而采用繁琐的穷竭法,但该方法始终是一个有限的过程,与当今所说的极限还有一定的距离,依靠该方法也难以发现新的结论. 所谓类比法,就是先证明正多边形的面积等于周长与边心距的乘积之半,然后将圆视为“正无穷边形”,从而得到圆面积为其周长与半径的乘积之半.19种教科书采用了该方法.例如,17世纪法国数学家奥泽南(J.Ozanam, 1640—1717)在《实用几何学》[7](1684)中通过将正多边形转化为三角形(图4),证明其面积等于底边长等于周长、高等于边心距的三角形面积,然后将圆看作“正无穷边形”,直接得出圆面积公式. 图4 正多边形的等积变形 18世纪法国数学家拉梅(B. Lamy, 1640—1715)在其《几何基础》[8](1731)中、布尔格尼(L.de Bourgogne)在其《几何基础》[9](1735)中、瓦里尼翁(P.Varignon,1654—1722)在其《数学基础》[10](1734)中、克莱罗(A. C. Clairaut,1713—1765)在其《几何基础》[11](1753)中、英国数学家米勒(J. Muller, 1699—1784)在《新数学基础》[12](1773)中都采用了这种方法. “正无穷边形”一说源于微积分发明者之一莱布尼茨(G. W. Leibniz, 1646—1716)的切线定义.18世纪,微积分尚未严密化,极限概念还不清晰,这种说法为数学家所普遍采用. 79种教科书利用“极限”工具来推导面积公式.有些教科书证明:当圆内接或外切正多边形边数n趋向无穷时,其周长(分别用pn和Pn表示)和面积(分别用sn和Sn表示)的极限分别是圆周长C和圆面积S;有些教科书则不加证明地直接利用了上述结论.不同教科书推导或证明圆面积公式的方法有以下几种情形. 3.4.1 三角形法 图5 开普勒圆面积公式推导 18世纪法国数学家布尔格尼除了将圆视为“正无穷边形”外,还将圆视为“由无穷多个同心圆构成的图形”,把每一个圆周“拉直”,圆就转化成了直角边长分别等于圆周长和圆半径的直角三角形.这种方法源于17世纪意大利数学家卡瓦列里(B. Cavalieri, 1598—1647)的“不可分量法”,其基本思想是:线由点构成,面由线构成,体由面构成.如图6,过半径OA的端点A作圆的切线,取点B,使AB的长度等于圆周长,联结OB.过OA上任意一点C作OA的垂线,交OB于D.易证:CD等于以OC为半径的圆的周长.因此,圆O的面积等于Rt△OAB的面积[9].里瓦尔德(F. Rivard, 1697—1778)在其《几何基础》(1739)和《数学基础》(1752)中也采用了同样的方法.[17-18] 图6 同心圆方法 Slaught(1911)则不通过等积变形,而直接将无穷多个小三角形的面积相加得到圆面积公式[19],如图7所示. 图7 Slaught(1911)对圆面积公式的推导 3.4.2 平行四边形法 3种教科书采用了平行四边形法.Lardner(1840)采用了该方法.以圆心为顶点,将圆划分为数个全等的扇形,相应数量的相等扇区之和便是圆的面积.无限划分扇形,沿某一扇形半径展开,将每个小扇形弧边上两个点相接,把两个如此操作的圆拼在一起时可以更直观地得到一个圆的面积等于其周长与半径乘积之半(见图8).[20] 图8 Lardner(1840)中平行四边形拼接 Schoch(1904)将圆内接正n边形中的n个等腰三角形移到同一直线上,且相邻两个三角形有一个公共顶点,将图形补成一个矩形如图9所示,易见,圆内接正n边形的面积等于矩形面积之半,即正n边形边长与边心距乘积之半. 图9 圆内接n边形的面积 类似地,如图10所示,将圆分割成许多小扇形,将小扇形移到一排,其中相邻两个扇形有一个公共点;将其补成一个近似的长方形,得到圆面积等于周长与半径乘积之半.[21] 图10 Schoch(1904)中的圆面积求法 Willis(1922)则将圆等分割成许多小扇形,然后将它们拼成近似平行四边形(图11(2)).作者设问:需要将圆分成几部分才能拼成图11(3)的样子?该矩形的底与高各是多少?由此可得圆面积吗?[22]显然,矩形的底是圆的半周长,矩形的高是圆的半径.因此,当分割的份数无限大时,圆面积等于矩形面积. 图11 Willis(1922)关于圆面积公式的证明 该方法较之仅仅将圆分割成三角形割开来算更加直观,对比起“极限法”来说更便于理解,也是当今教科书多采用的方式.但是在早期教科书中出现较晚且次数寥寥,究其原因,其一,在早期,人们在证明方式与思想上受阿基米德的影响,运用正多边形逼近圆并追求严谨的证明过程;其二,20世纪之初,“培利运动”促使数学教育注重几何直观,主张学生更多地自主探求数学中的规律而非教师引导下进行空洞的逻辑推理,此时教科书才开始将学生的认知基础作为知识的发生点,运用直观的等积变形进行几何知识的教授. 以世纪为单位,图12给出了各个方法的时间分布. 图12 四种证明方式的时间分布 圆面积推导方法的演变呈现出由单一走向多元,最终回归单一的趋势. 穷竭法源于古希腊,是当时数学家在“患”上“无穷恐惧症”、不接受实无穷的情况下所设计的方法.受古希腊数学的深刻影响,穷竭法在17—19世纪不绝如缕,少数教科书运用它以避开“无穷”概念.随着微积分的创立与发展,人们逐渐接受“无穷”概念,穷竭法逐渐被抛弃,类比法和等积变形法登上了历史舞台;而随着19世纪微积分的严密化和极限概念的完善,极限法后来居上,最终成为主流方法. 18世纪到20世纪之间,直观性较强的“等积变形法”一直有一席之地,它是最符合低学段学生的方法,并且体现了数学研究“数形结合”的特点. 以上我们看到,圆面积公式大致经历了从穷竭法到类比法、再到等积变形法、最终到极限法的历史发展过程,体现了极限概念从无到有、不完善到完善的演进过程.圆面积公式的历史为我们提供了若干教学启示. (1)运用类比,发现结论.首先让学生观察正多边形随着边数越来越多,形状越来越像圆;接着,通过等积变形,将圆内接正多边形转化为三角形(图4),得到正多边形面积公式;最后,通过类比,猜想圆可以转化为三角形(图5),进而得到圆面积公式.或者,首先让学生观察:两组同样的三角形(每一组含1个、2个、3个、4个等等)可拼成平行四边形;接着,将同样两个圆的内接正多边形中的各个等腰三角形剪下来,拼成平行四边形;最后,通过类比,猜想得到两个圆可以转化为一个平行四边形,进而得到一个圆的面积. (2)通过技术,实现转化.同心圆方法源于17世纪卡瓦列里的“不可分量法”,在今天看来并不严密,通过技术(如利用Geogebra软件),可以让无穷小方法可视化:先将圆分割成一系列同心圆环,依次将这些圆环“拉直”,拼成近似三角形,然后让诸圆环不断变细、从而得到相应的图形越来越接近真实的三角形. (3)关注方法,联系古今.历史上出现了圆面积公式的许多推导或证明方法,教师可以设计探究活动,让学生分享自己的方法,并通过“古今联系”的策略进行评价,让学生穿越时空与数学家对话,成为课堂的主人.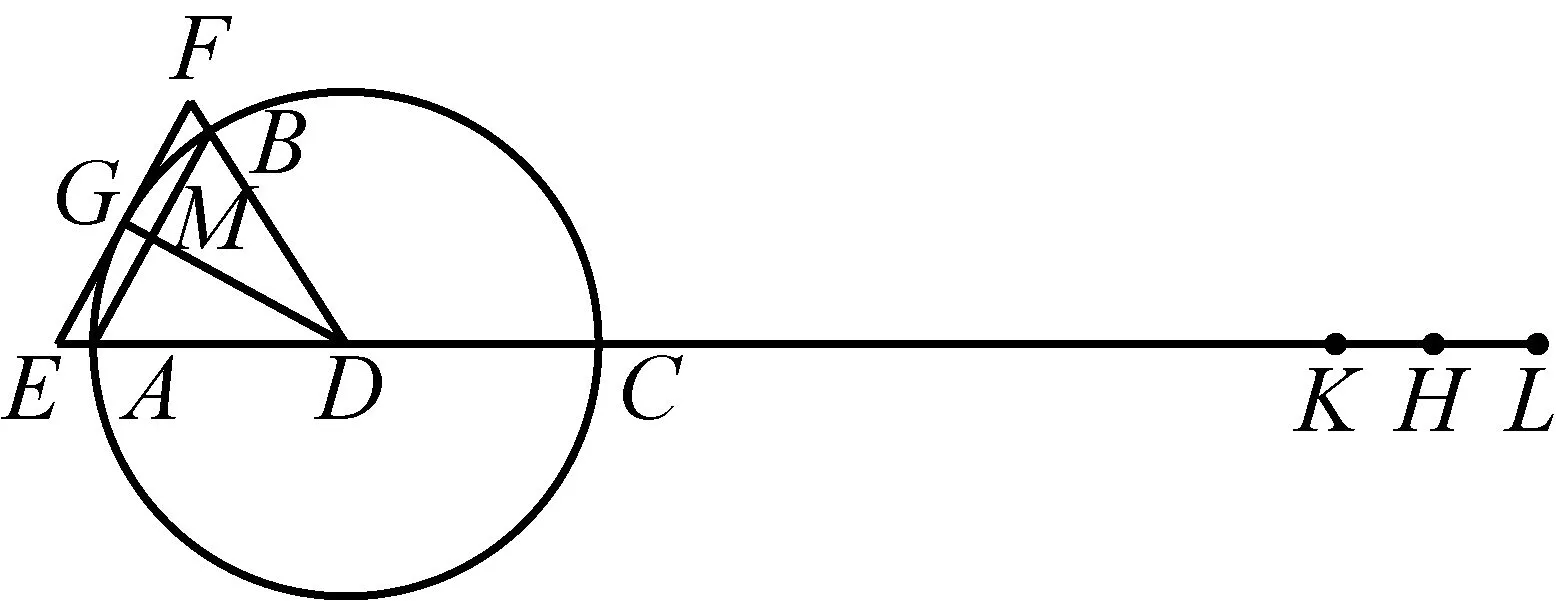
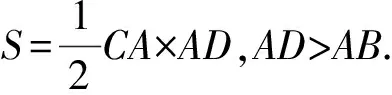
3.2 类比法
3.3 极限法
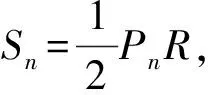
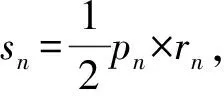

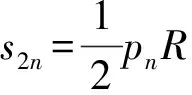
3.4 等积变形法




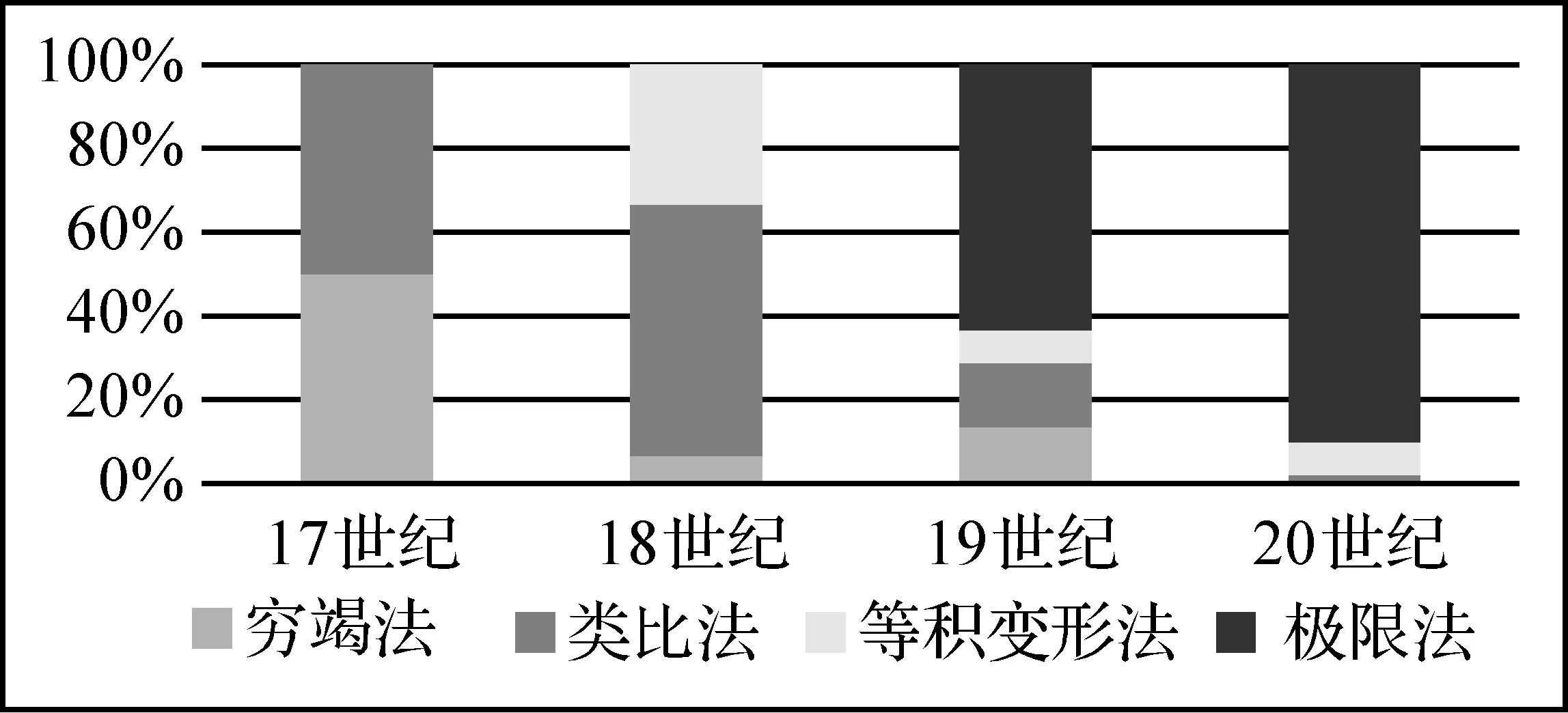
4 证明方式的演变
5 教学启示

