再谈“陪位中线”
崔 浩
(北京市第十二中学 100071)
《数学通报》2019年第12期发表汪学思老师关于三角形陪位中线的文章(以下简称文[1]),读后深受启发.巧合的是,笔者在长期数学竞赛辅导工作中,也发现三角形陪位中线有着广泛的运用,于是,在研读文[1]的基础上,对陪位中线从作法到证明,从性质到应用,以及学生在课堂上的若干意外生成,做了进一步地研究与思考,侥幸有了一些新的发现,现不揣浅陋,特向同行汇报一下自己的研究结果,以期得到专家的指正.
1 作法
考虑到三角形的陪位中线并非平面几何中的主干内容,为方便读者,重温陪位中线的定义:
图1
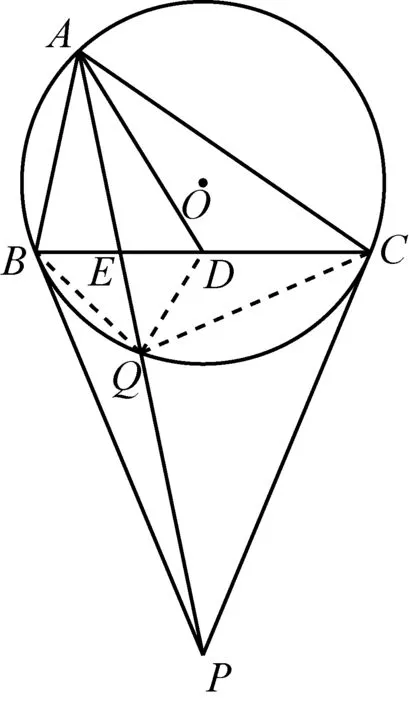
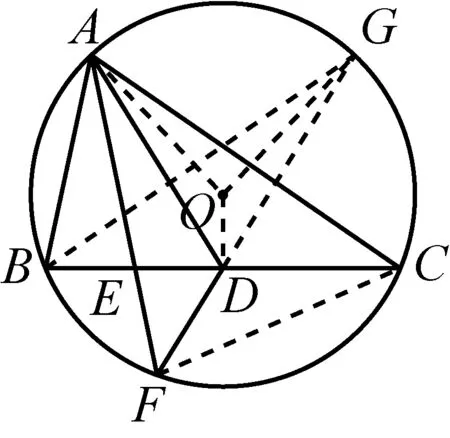
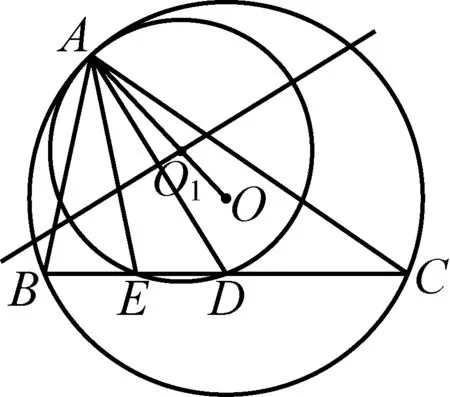
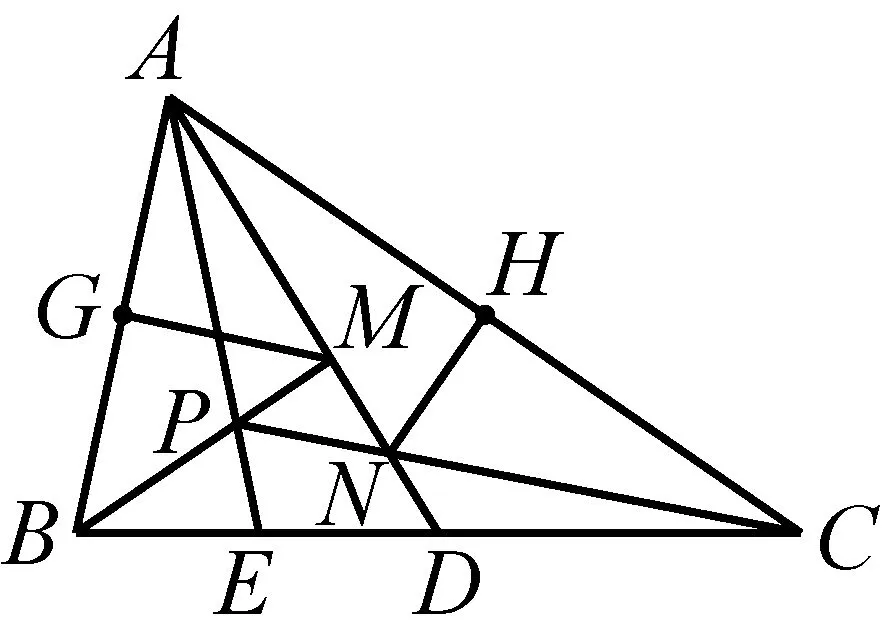
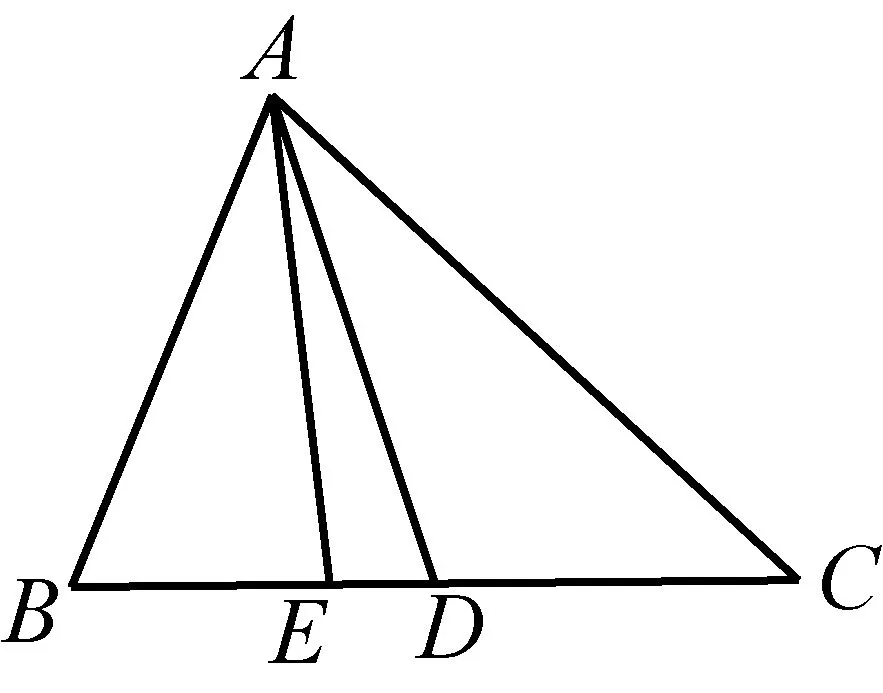
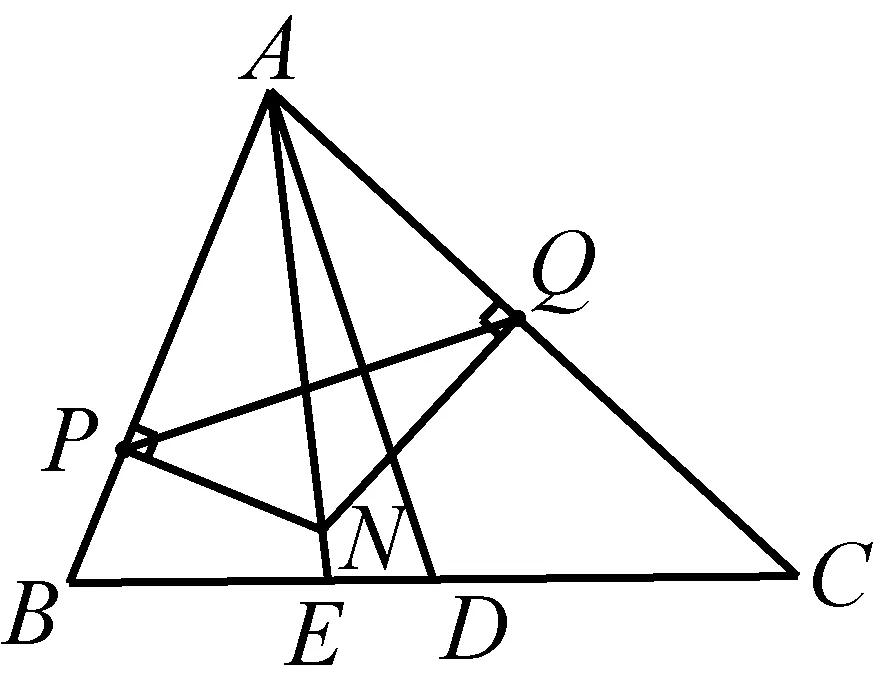
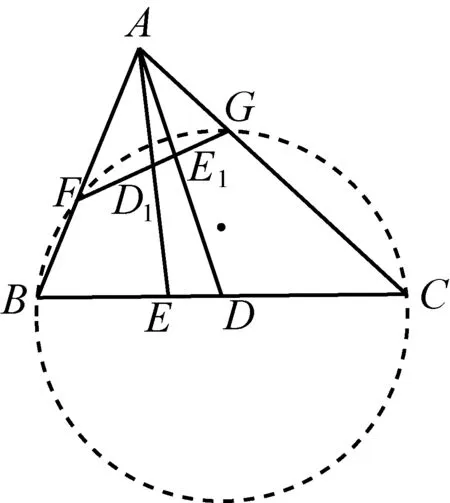
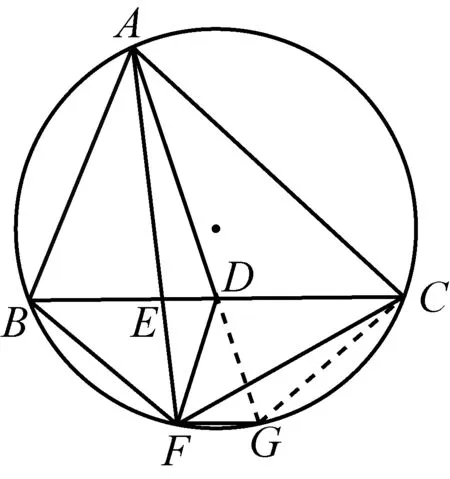
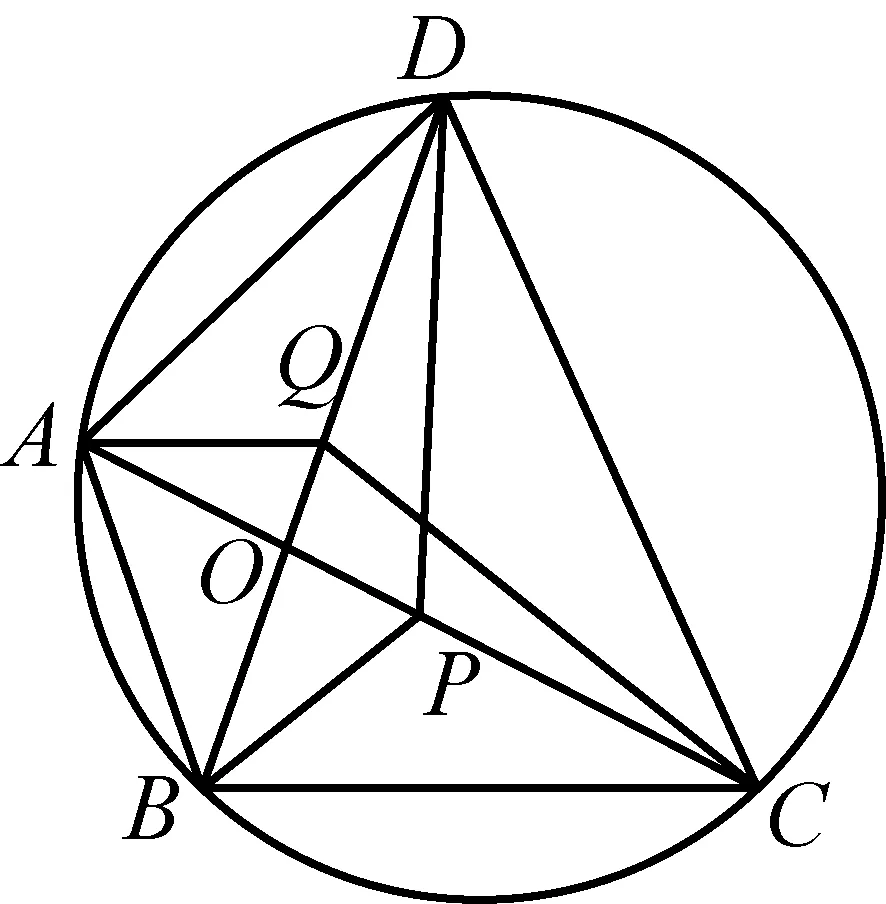
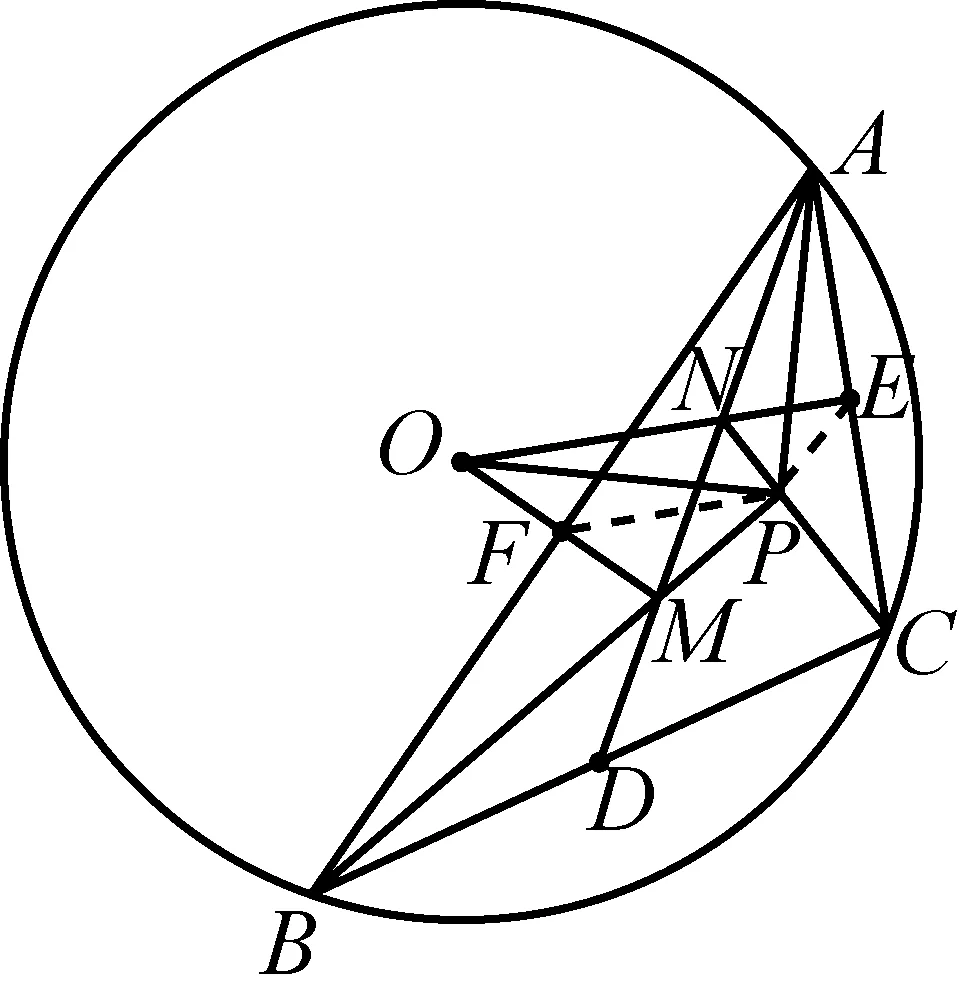
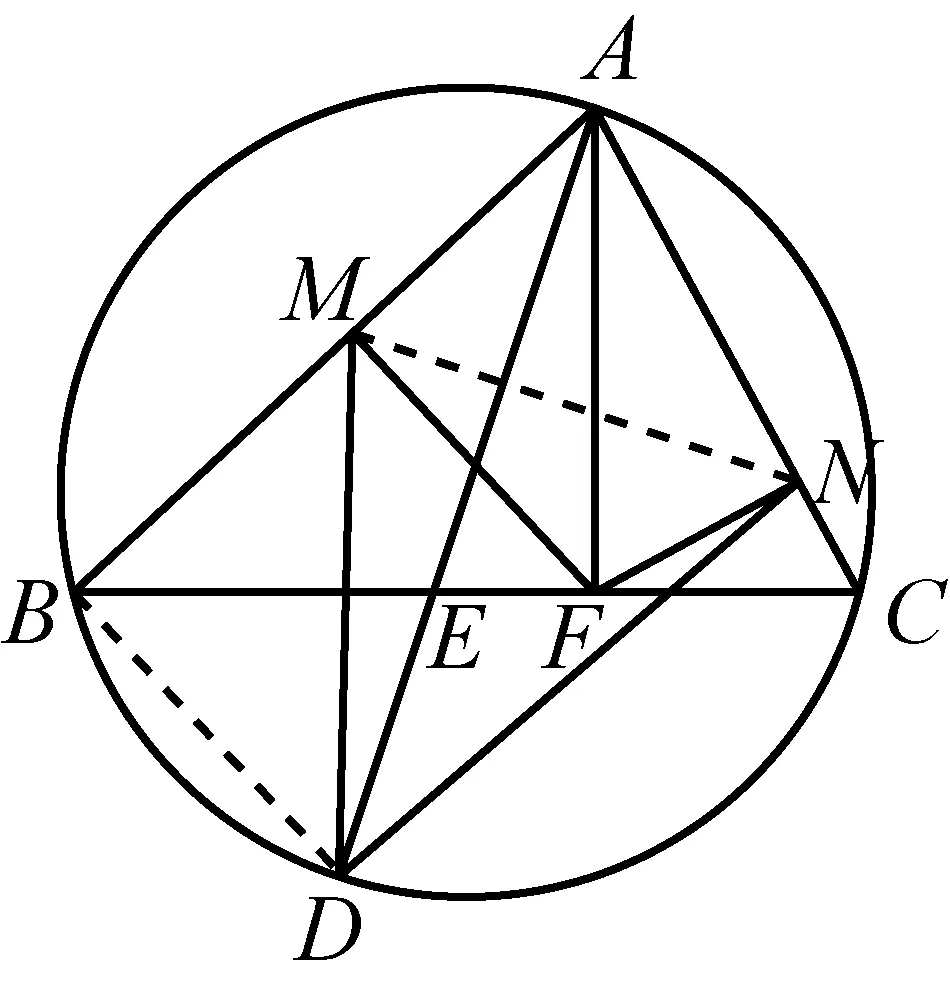
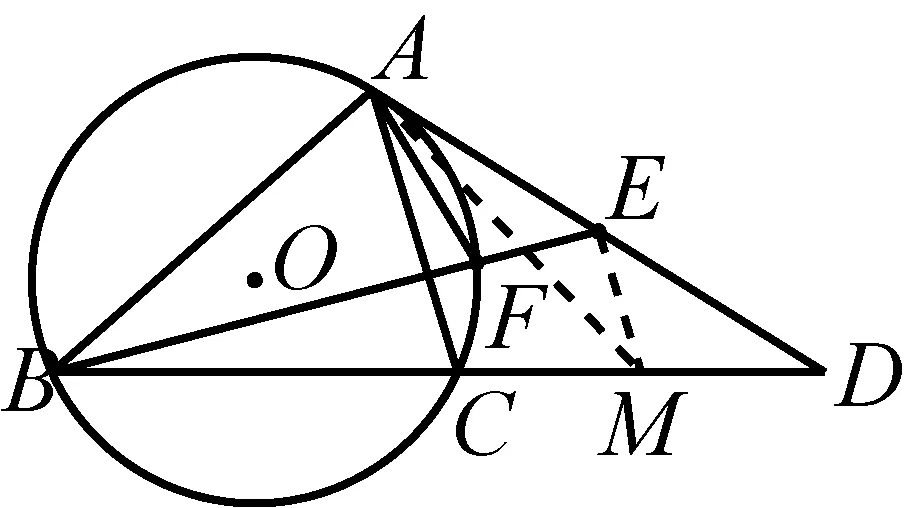
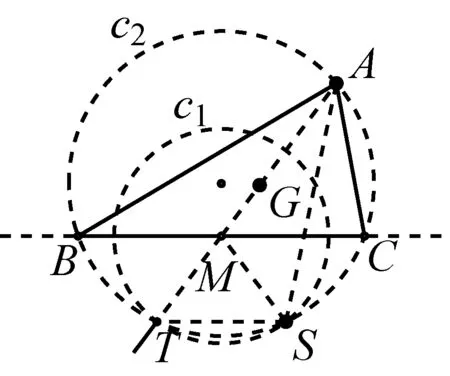
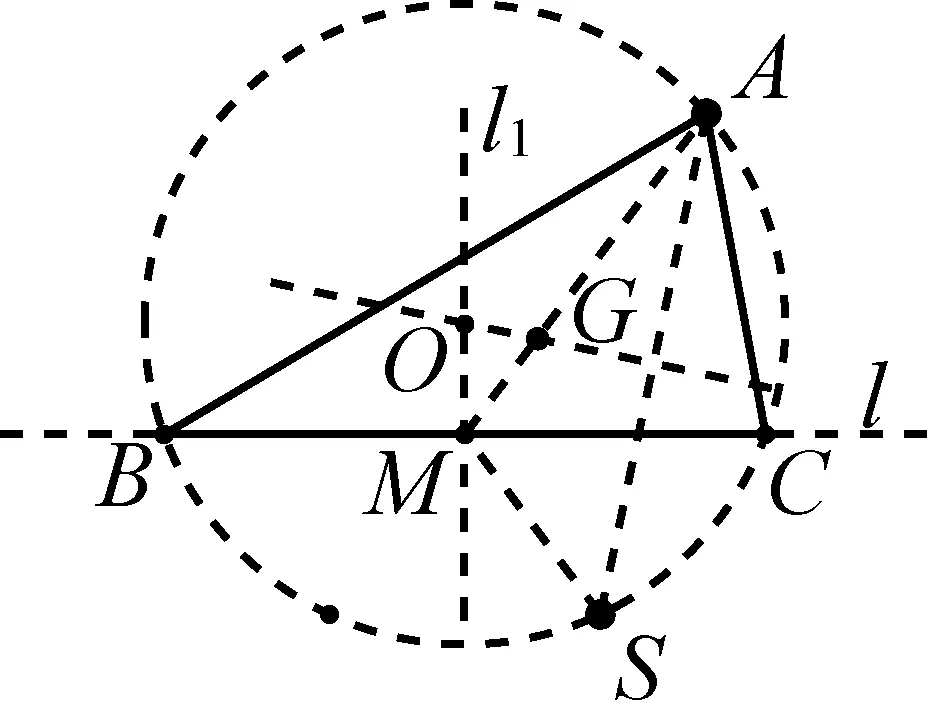
如图1,已知AD是△ABC(AB 图2 (1)作法1如图2,AD是△ABC(AB (2)作法2如图3,过B,C两点作不过点A的圆O, 与直线AB、AC分别交于点F、G,FG的中点为M,AM与BC交于点E,则AE是△ABC边BC上的陪位中线. 图3 (3)作法3如图4,作△ABC的外接圆O,分别过点B、C作圆O的切线,两条切线交于点P,连接PA交BC于点E,则AE是△ABC边BC上的陪位中线. (说明:这里△ABC的内角∠BAC是锐角,至于∠BAC是钝角的情形,限于篇幅,留给有兴趣的读者完成.) 证明如图4,记AP与圆O交于点Q, 连接BQ和CQ, 图4 因为PB是圆O的切线, 因为PC是圆O的切线, 即AB·CQ=AC·BQ. 由托勒密定理得 AQ·BC=AB·CQ+AC·BQ, 又D为BC的中点, 所以AQ·2DC=2AC·BQ, 又∠AQB=∠ACD, 所以△AQB∽△ACD, 所以∠CAD=∠BAE, 即AE是△ABC边BC上的陪位中线. 上面我们证明了△AQB∽△ACD,连接DQ,容易证明△AQB∽△CQD,所以△ACD∽△CQD,进而得出∠ADC=∠CDQ,即射线DA与射线DQ关于BC对称,在此基础上可得出作法4. (4)作法4如图5,作射线DA关于BC对称的射线,交△ABC的外接圆O于点F,连接AF交BC于点E,则AE是△ABC边BC上的陪位中线. 证明如图5,连接OA、OD,作半径OG,使∠AOD=∠GOD,连接GB、GD、FC,则△AOD≌△GOD,所以DA=DG,∠ADO=∠GDO. 图5 (5)作法5如图6,作△ABC的外接圆O,连接OA,与AD的中垂线交于点O1,以O1为圆心以O1A为半径的圆,交BC于点E,则AE是△ABC边BC上的陪位中线. 图6 (6)作法6如图7,作边AB的中垂线GM,交AD于点M,作边AC的中垂线HN,交AD于点N,直线BM与CN交于点P,作直线AP交BC于点E,则AE是△ABC边BC上的陪位中线. 图7 所以∠ABM=∠BAM=θ-α, 因为HN是边AC的中垂线, 所以∠ACN=∠CAN=α, (1) (2) 因为D是BC的中点, 所以ACsinα=ABsin(θ-α), 所以sin(θ-β+α)-sin(θ-α+β)=0, 所以2sin(α-β)cosθ=0. 所以∠CAD=∠BAE, 所以AE是△ABC边BC上的陪位中线. 如图8,已知AD是△ABC边BC上的中线,AE是△ABC边BC上的陪位中线,则有下列四条常用性质. 图8 性质1(陪位中线长) 记AB=c,BC=a,CA=b,则 证明(1)见文[1]第54页. (2)由斯特瓦尔特定理得 b2BE+c2EC=a·BE·EC+a·AE2(*), 由(1)和BE+EC=a可得 代入(*)并化简得 (3)又由斯特瓦尔特定理可得 从性质1(3)可以看出,三角形边上的中线长不小于它对应的陪位中线长. 性质2如图8-1,设N是AE上任一点,点N在AB、AC上的射影分别为P、Q,则 图8-1 证明(1)因为N在AB、AC上的射影分别为P、Q,所以 NP=ANsin∠BAE,NQ=ANsin∠CAE, 所以 因为D是BC的中点, 所以ABsin∠BAD=ACsin∠CAD, (2)又N在AB、AC上的射影分别为P、Q可得A,P,N,Q四点共圆,所以∠PAE=∠PQN,因为∠BAE=∠CAD, 所以∠PQN=∠CAD, 所以PQ⊥AD. 值得注意的是,性质(2)的证明没有用到D是BC中点的条件. 性质3如图8-2,过B、C两点的圆与AB、AC分别交于点F、G,FG分别与AE、AD交于点D1,E1,则AD1,AE1分别是△AFG的中线和陪位中线. 图8-2 证明由题意,B,C,G,F四点共圆, 所以∠AFG=∠ACB, 因为∠BAE=∠CAD, 所以△AFD1∽△ACD, 又由B,C,G,F四点共圆得△ABC∽△AGF, 因为D是BC的中点,所以D1是FG的中点, 即AD1,AE1分别是△AFG的中线和陪位中线. 性质4(有关外接圆)如图8-3,若AE与△ABC外接圆O的交点为F,则 图8-3 (1)射线DA、DF关于BC对称; (2)FE是△FBC的边BC的陪位中线; (3)四边形ABFC是调和四边形(1)若圆的内接四边形的对边乘积相等,则称此四边形为调和四边形.. 所以BF=GC,且∠DBF=∠DCG, 因为D为BC的中点, 所以△BFD≌△CGD,所以∠BDF=∠CDG, 因为∠ADB=∠CDG,所以∠BDF=∠ADB, 即射线DA、DF关于BC对称; (2)由作法4,根据(1)的结论知: FE是△FBC的边BC的陪位中线; (3)由题意得∠BAF=∠DAC, 因为∠AFB=∠ACD, 所以△ABF∽△ADC, 所以AF·DC=BF·AC, 因为D为BC的中点, 所以AF·BC=2BF·AC, 由托勒密定理得 AF·BC=BF·AC+FC·AB, 所以BF·AC=FC·AB, 故四边形ABFC是调和四边形. 例1(2011年全国高中联赛加试第一题)如图9,P,Q分别是圆内接四边形ABCD的对角线AC,BD的中点,若∠BPA=∠DPA,证明∠AQB=∠CQB. 证明记AC与BD交于点O,由题意,结合作法4知DO是△ACD的陪位中线,再由性质4(3)知,四边形ABCD是调和四边形, 因为∠ABQ=∠ACD,所以△ABQ∽△ACD. 因为∠CBQ=∠CAD,所以△BCQ∽△ACD, 所以△ABQ∽△BCQ,故∠AQB=∠CQB. 图9 例2(2013年东南数学奥林匹克)如图10,在钝角△ABC中,AB>AC,点O是其外心,边BC、CA、AB的中点分别为D、E、F,中线AD与OF、OE分别交于点M、N,直线BM、CN交于点P,证明:OP⊥AP. 图10 证明由题意,得FM、EN分别是AB、AC的中垂线,结合作法6,可得AP在边BC的陪位中线上, 所以∠BAM=∠ABM=∠PAC, ∠NAC=∠NCA=∠BAP, 因为E、F分别是AC、AB的中点, 所以△BFP∽△AEP,所以∠BFP=∠AEP, 故F,P,E,A四点共圆, 由OF⊥AB,OE⊥AC得O,F,E,A四点共圆, 所以O,F,P,E,A五点共圆, 所以∠OPA=∠OEA=90°,即OP⊥AP. 例3(2000年全国高中联赛加试第一题)如图11,锐角△ABC的边BC边上有两点E、F,满足∠BAE=∠CAF,作FM⊥AB,FN⊥AC(M,N为垂足),延长AE交三角形ABC的外接圆于点D,证明:四边形AMDN与△ABC的面积相等. 图11 例4(文[1]例7) 如图12,在△ABC中,AB>AC,过点A作△ABC的外接圆⊙O的切线,与BC的延长线交于点D,E为AD的中点,BE与⊙O交于点F,求证:AF在△ACD的边BC的陪位中线上. 图12 分析文[1]中给出的两种证明都用了性质,若回到定义中去证明,则想法更自然、过程更简洁. 证明取CD的中点M,由题意EM是△ACD的中位线,所以∠DEM=∠DAC, 因为∠DAC=∠ABD,所以∠DEM=∠ABD,故A,B,M,E四点共圆, 所以∠MAD=∠DBE, 因为∠CAF=∠DBE,所以∠CAF=∠MAD, 所以AF在△ACD的边BC的陪位中线上. 例5(文[1]例5)如图13,在△ABC中,已知顶点A、重心G和其经过A点的陪位中线所在直线与△ABC外接圆的交点S,然后擦去点B、C及其外接圆,请从保留的三个已知点A,G,S出发,作图画出原△ABC. 图13 文[1]中的解法可概括为如下六个步骤,如图13-1: 图13-1 ②以M为圆心,以MS为半径作圆c1; ③设AM的延长线交圆c1于点T; ④作△AST的外接圆c2; ⑤过M作TS的平行线交圆c2于点B、C; ⑥连接A、B、C,则△ABC即为所求. 上述解法完全正确,笔者由衷佩服文[1]作者超强的解题能力,但从我的学生角度看,他们对解题过程一定会心生疑惑,如在第②、③两步,怎么想到要作点T?第⑤步作TS的平行线,学生很难想到.如果做法不能给出自然、平实的解释,那么很难内化为学生的能力,无疑会使解题教学的效益大打折扣.事实上,若学生掌握了陪位中线性质4(2),下面的作法就可以自然生成,如图13-2: 图13-2 ②连接MS,作∠AMS平分线所在的直线l; ③过点M作直线l的垂线l1; ④作AS的中垂线与直线l1的交点记为O; ⑤以O为圆心,以OA为半径的圆与直线l的交点为B,C; ⑥连接A、B、C,则△ABC即为所求. 综上所述,陪位中线是三角形中的重要元素,本文所汇集的几种陪位中线的作法,大多由竞赛辅导教学中师生思维火花碰撞而成,所附带的作法证明,主要通过构造三角形相似、利用四点共圆以及三角计算完成,这又为平面几何证明提供了丰富的训练素材.至于陪位中线性质的提炼,基本是教学中师生互动探究的结果.实践表明,带领学生系统地研究陪位中线作法、性质及其证明,对学生在复杂的问题情境中识别陪位中线问题的模型,预判解决(证明)问题的方向,大幅度提升解决问题的能力,是非常有益的.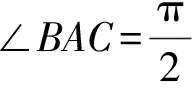

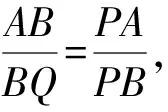
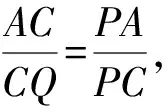
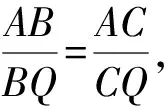
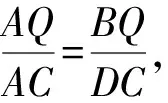
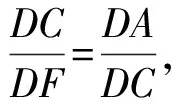
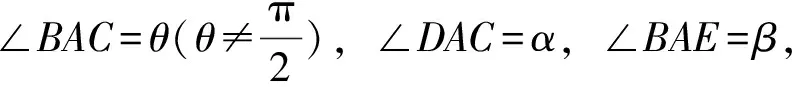
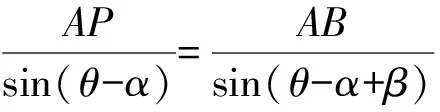
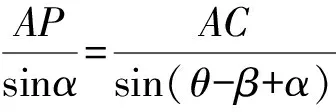
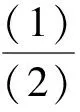
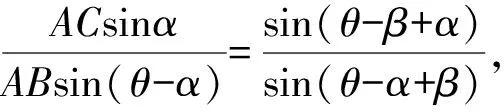
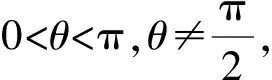
2 性质
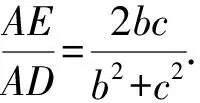
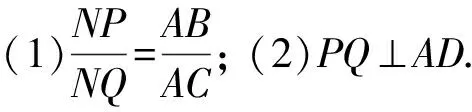
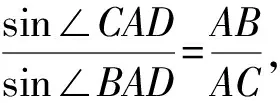
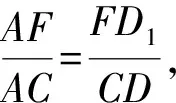
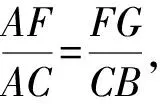
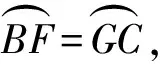
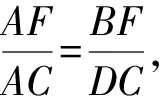
3 应用
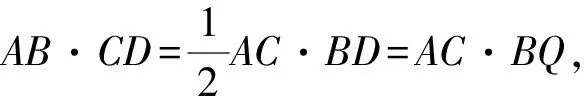
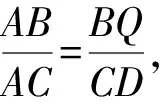
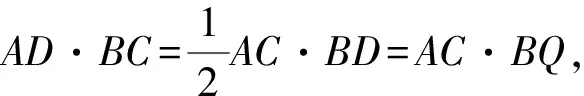
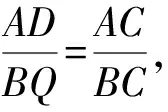
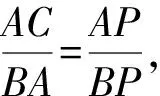
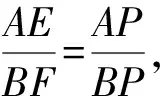
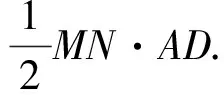
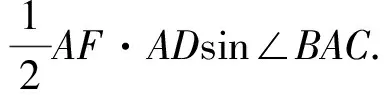
4 文[1]拾遗
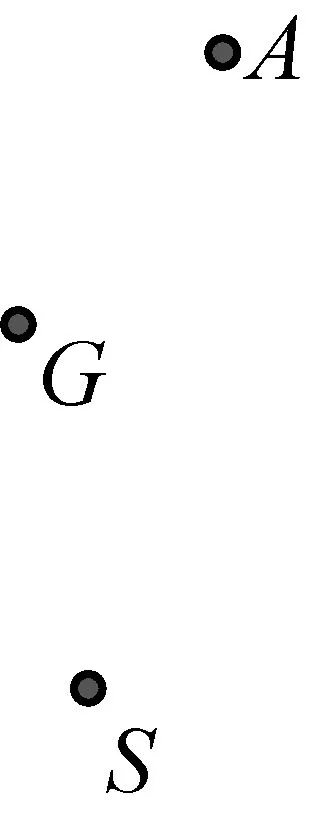
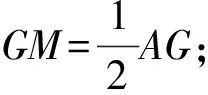
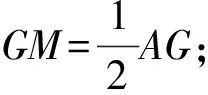
5 结束语

