基于大型振动台试验的堆积型边坡峰值加速度放大性智能预测方法研究
王 翔,李宗昊,王 栋,郭雪岩,杨长卫,裴向军
(1.北京交通大学 土木建筑工程学院, 北京 100044;2.西南交通大学 土木工程学院,四川 成都 100084;3.中铁二院工程集团有限责任公司,四川 成都 610031;4.地质灾害防治与地质环境保护国家重点实验室,四川 成都 610059)
地震作用下边坡稳定性的研究是目前岩土方向的研究重点之一,我国接近半数的国土面积处于0.1g及以上的高地震危险区,且大部分地震频发带位于山区,一旦发生强震,极易诱发严重的边坡问题[1]。目前,振动台试验是在实验室模拟地震的重要手段,比较接近实际地震时地面的运动情况以及地震对结构物的作用情况,是研究结构物在地震作用下的破坏机理和破坏模式、评价整体抗震能力的重要手段和方法,在地震工程的理论研究和工程实际中已经得到了广泛的应用[2]。PGA是目前地震研究中普遍使用的参数,探寻一种快速、可靠、有效地估计PGA方法是目前地震研究中一项需要考虑的问题[3]。国内外专家、学者开展了大量的研究工作[1-6],先后提出了边坡峰值加速度的放大系数,但主要集中在定性研究,针对定量来的研究成果甚少,且主要集中在针对单一边坡开展分析,大大限制了研究成果的适用性。然而,随着人工智能、大数据技术的不断进步,人工智能逐渐成为岩土工程的热点发展方向之一,且人工智能算法随着基础性数据的增长,计算精度逐渐提升[7-10]。
基于此,本文将基于大量振动台试验数据,综合考虑边坡参数、地震波参数及土体参数等各项因素的影响,建立了基于随机重连型BP神经网络的堆积型边坡峰值加速度放大性智能预测模型,并借助模型试验和鲁棒性分析对上述模型的计算精度进行了验证和稳定性进行了研究,能够为高烈度山区铁路边坡支护结构的抗震设计提供直接参考,有助于推进岩土工程智能化的发展。
1 振动台试验简介及预测指标体系
本次振动台试验装置采用单向地震模拟振动台,试验模型采用均质材料,在模型制作的时候采用现场浇筑方式建造试验模型。该地震模拟台承载能力大,性能先进,能够满足堆积边坡振动台试验要求。振动台台面尺寸为3 m×3 m,台面结构为钢焊单层网格。台面最大承载量为20 t,最大速度为0.7 m/s2,最大加速度为±2.0g,工作频率为0.1~50 Hz,位移范围±125 mm。以40°边坡和60°边坡进行展示。
本次边坡试验模型缩尺比例为1∶10,边坡坡角分别为40°、45°、50°、55°、60°,每组试验的土体密度、黏聚力、内摩擦角均不相同;输入地震波类型分为三种:汶川卧龙地震波、Kobe地震波以及EL Centro地震波且地震波的峰值加速度分别为0.1g~1.0g,依次从小到大输入,见图1。为了更准确地模拟地震前场地环境,在输入每个峰值加速度之前对试验模型进行0.05g白噪声扫频处理,共计150组振动台试验,具体试验工况见表1。

图1 归一化后地震波时程(1.0g)

表1 振动台加载工况
由于本试验旨在研究地震波类型、频率以及振幅对堆积边坡动力的响应规律,故首先对输入地震波进行归一化处理,之后通过调节其幅值来施加不同加速度峰值的单向地震动时程[4],整个试验均采用三向加速度计测定加速度,为了更加准确地描述地震作用下边坡加速度响应的规律,一般以各监测点的实测动力响应加速度峰值PGA与台面输入加速度峰值的比值作为评定标准,以下称为PGA放大系数[5]。影响PGA放大系数的因素众多,在本次试验中,主要测定了以下参数:①边坡参数:坡角、滑体与基岩的体积比;②地震波参数:地震波波型、地震波最大峰值加速度;③土体参数:密度、黏聚力、内摩擦角。基于此,本文将以上述7个因素作为预测模型中指标评价体系的基本因素。
2 随机重连型BP神经网络模型
人工神经网络是一种基于人脑所建立的模型,其拥有由数量巨大的神经元所组成的系统,有大规模并行、分布式处理、自组织、自学习等优点[6]。BP神经网络作为目前适用性最广的一种算法,具备自适应能力、容错率高等优点,其基本原理是信号前项传递,误差反向传播[11]。在前向传递中,输入信号从输入层经隐含层逐层处理,直至输出层;如果输出层得不到期望输出,则转入反向传播,根据预测误差调整网络权值和阈值,从而使整个网络预测输出不断靠近期望输出,直至达到误差精度要求。鉴于篇幅限制,随机重连型BP神经网络的推导过程将不予阐述,具体模型结构见图2。

图2 随机重连型BP神经网络结构
本文以三层随机重连型BP神经网络为例,介绍其基本原理。
(1)隐含层节点输出为
y=f(∑wjixi-θj)=f(netj)
(1)
式中:xi为输入节点;yj为隐含层节点;wji为输入节点与隐含层节点间的连接权值;θj为隐含层各神经元的阈值;f为隐含层和输出层的激励函数;tj为输出节点的期望[12];i,j分别为输入节点、隐藏层节点序号。
(2)输出层节点输出为
(2)
式中:zl为输出节点;vlj为隐含层节点与输出节点间的连接权值;θl为输出层各神经元的阈值;l为阈值序号。
(3)实际输出与期望输出间的均方误差函数为
(3)
(4)误差函数对隐含层与输出层节点间的权值求导为
(4)
式中:E为zk的函数;k为权值序号。
但是只有zl与vlj有关,zi与zj(i≠j;i,j=1,2,…,n)间相互独立,则有
(5)
式中:f′为激励函数的导数。
(5)设输出层节点误差为
δl=(tl-zl)×f′(netl)
(6)
误差函数对输入层与隐含层节点间的权值wlj求导,可得
(7)
式中:E为zl(1≤l≤n)的函数。
某一个wji对应于一个yj,它与所有的zl(1≤l≤n)有关,则有
(8)
(6)设隐含层节点误差为
(9)
由于权值的修正比Δvlj、Δwji于误差函数沿梯度下降,故隐含层与输出层节点间的权值变化为
(10)
式中:η为隐含层与输出层的学习率。
隐含层与输出层节点间的权值修正为
vlj(k+1)=vlj(k)+Δvlj=vlj(k)+ηδlyj
(11)
输入层与隐含层节点间的权值变化为
(12)
输入层与隐含层节点间的权值修正为
(13)
式中:η′为输入层与隐含层间的学习率;k为样本个数。
在调整权值的同时,阈值也会调整,其原理与权值相同。
误差函数对输出节点阈值求导
(14)
阈值调整为
(15)
θl(k+1)=θl(k)+ηδl
(16)
误差函数对隐含层节点阈值求导,可得
(17)
阈值调整为
(18)
(19)
3 基于随机重连型BP神经网络的堆积式边坡峰值加速度放大系数智能预测模型

本次振动台试验共有150组数据,随机取其中120组作为训练集,用以训练网络,剩下30组作为验证集,用以检测该网络是否达到精度要求。在输入数据前,要对地震波类型进行数字代号替换,地震共有三种,EL Centro波为1,汶川卧龙波为2,Kobe波为3。
针对本次试验,本文选取适用性最好的tarinlm算法,即Levenberg-Marquardt 算法,对于小型网络,其精度最高且训练时间最短,在该算法中需要提前设置关键技术参数,如下:动量mu取0.001,动量梯度mu_dec取0.1,动量分量mu_inc取10,训练整体精度要求达到0.001,其他参数设置参照文献[14]。随机选取表2中120组数据作为训练样本,余下30组作为验证样本,部分训练结果见表2,120组数据的对比折线图见图3。
随机从训练样本中抽取数据见表2,由表2可知,该模型训练精度误差均低于10%。训练120数据对比见图3,由图3可知,训练数据总体趋势基本符合原始数据。在实际的试验中,总会存在一定误差,故该模型训练结果良好,可用余下30组数据作验证,验证集不提供输出层数据,只提供输入数据,利用训练的模型来计算出输出层数据,验证数据见表3,验证的30组数据的对比折线图见图4。

图3 训练120组数据对比折线图

图4 验证30组数据对比折线图
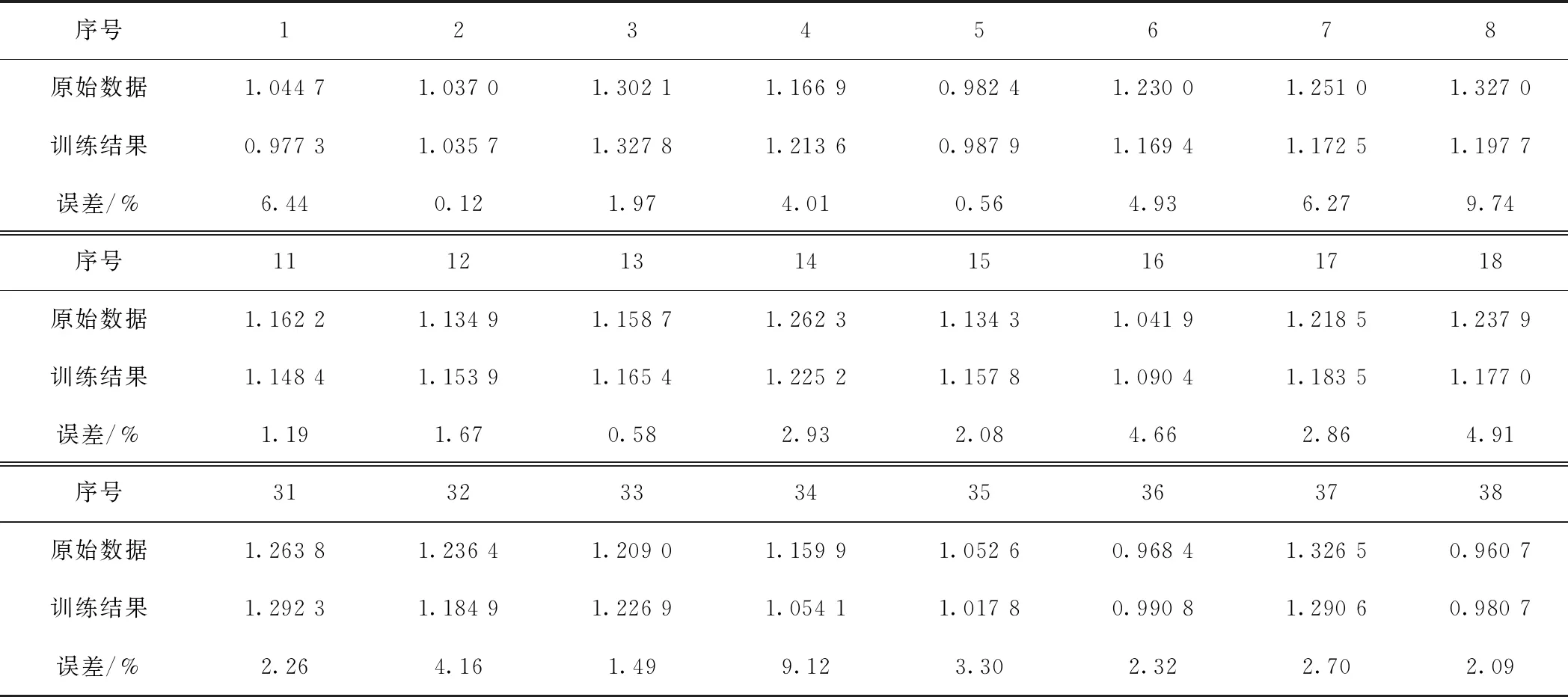
表2 训练结果

表3 模型验证结果
由表3可知,验证结果良好,误差均低于10%,由图6可知,原始数据与模型验证数据整体趋势近乎相同,存在少量误差,故该模型的训练效果良好。
4 鲁棒性分析
对于机器学习,鲁棒性也是一个重要的特性,人工神经网络本身是具有鲁棒性的[15];对于BP神经网络,鲁棒性是指在少部分数据受到污染的情况下,神经网络模型计算结果并不会受到较大的影响[16]。假设30组验证数据受到随机干扰,见表4,代入建立的模型,进行鲁棒性测试。

表4 污染数据
鲁棒性测试结果见表5,试验原始测得放大系数、未污染数据算得放大系数、受污染数据算得放大系数对比折线图见图5;由表5和图5可知,部分数据收到干扰的情况下,少量计算结果有些许误差,或大于10%,但整体结果趋势与原趋势基本不变,说明该BP神经网络模型鲁棒性良好。
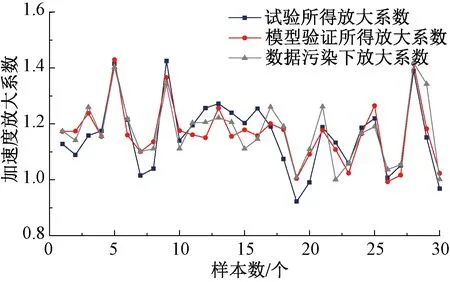
图5 污染数据计算结果对比

表5 污染数据计算结果
5 结论
地震加速度峰值(PGA)放大系数是研究地震作用的重要参数之一,本文基于前期完成的150组堆积型边坡大型振动台试验数据,提出了随机型重连BP神经网络模型,建立了基于随机重连型BP神经网络的堆积型边坡峰值加速度放大性智能预测模型。该模型能够系统考虑边坡参数(坡角、滑体与基岩的体积比)、地震波参数(地震波波型、地震波最大峰值加速度)及土体参数(密度、黏聚力、内摩擦角)的影响,模型预测结果与实际值相差较小,整体趋势相近,结论较为直观,能够为高烈度山区铁路边坡防护的抗震设计提供直接参考。
由于本项目中的各个影响因素之间关系复杂,不能直观用线性表达式来进行预测,故选择采用改进的BP神经网络对数据进行非线性处理,得到PGA放大系数。BP神经网络对于一组非线性的数据,不需要相对应的函数方程,仅通过自身的训练,不断迭代出相应的结果,得到一个满足要求的方程模型,即可以满足项目的要求,比传统方法更为有效便捷,神经网络在此非线性领域具有广阔的应用前景。
鉴于铁路沿线边坡实际工程的地质条件、水文条件及施工环境等因素极为复杂,存在各种不确定因素,仍需开展更为深入的研究。

