考虑不确定性的铁路信号安全计算机硬件SIL验证
张宏扬,梁志国,王龙生,齐志华,白 帅,乔亚琼
(1.中国铁道科学研究院集团有限公司 研究生部, 北京 100081;2.中国铁道科学研究院集团有限公司 通信信号研究所,北京 100081)
铁路信号安全计算机平台一般采用冗余配置,是基于失效—安全原则设计、须满足安全完整性等级(Safety Integrity Level,SIL)要求的高安全性计算机实时控制系统,在正式投入使用之前须由第三方认证机构进行SIL认证,其中硬件SIL验证是认证工作的重点,国内外有关学者对此做了大量研究。
文献[1-4]采用IEC 61508中提供的PFH(Probability of a dangerous Failure per Hour)公式[5]计算了不同冗余结构信号设备的安全完整性等级。文献[6-7]利用PDS方法[8]计算了某信号安全计算机的安全性指标PFH,进而验证其安全完整性等级满足相关的要求。文献[9-10]通过建立ATP(Automatic Train Protection)及其子单元的故障树来求解危险失效概率,由此判断所满足的SIL。另有一些文献采用马尔科夫链[11]、动态故障树[12-13]等动态方法对不同结构铁路信号设备的危险失效概率、安全完整性等级进行计算验证。上述文献在SIL验证中均假设失效率等相关参数为固定值,由此得到的是单一精确的安全性定量指标及对应的SIL,但在铁路信号系统的安全性分析中常存在失效数据不充足、失效模式未被完全辨识等客观因素,因此难以获取精确的故障数据,从而导致其硬件SIL的验证过程常受到不确定性因素的影响,但上述文献并未对此进行分析。而有研究对低要求模式下安全相关系统SIL验证中的不确定性进行了分析,如文献[14-15]利用蒙特卡洛法(Monte Carlo Analysis,MCA)模拟了常见冗余结构(Probability of dangerous Failure on Demand,PFD)公式中各参数概率分布已知类型的不确定性,有效减少了数据缺乏等不确定性因素对SIL验证结果的影响,但铁路信号领域内的失效参数通常难以获取其概率的分布类型,因此MCA的适用性也有限。模糊理论(Fuzzy Theory,FT)[16]可有效解决参数概率分布未知情况下的不确定性问题,有学者将其引入安全仪表系统的SIL验证中,如文献[17-18]将共因失效因子、诊断覆盖率的精确值替换为模糊数,并根据不同截集对结果进行判定,但截集取何值需要人为指定,从而可能二次引入不确定性,因此如何对结果进行评估须进一步考量。
综上,铁路信号设备SIL验证有关的文献大多未考虑验证过程中失效参数不确定性的影响,而常用的MCA、FT等不确定性分析方法多应用在安全仪表系统的SIL验证中。本文将上述应用在工业领域内安全相关系统SIL验证中的不确定分析方法引入铁路信号安全计算机的硬件SIL验证中,并对其进行改进。首先对铁路信号安全计算机常见冗余结构及其SIL验证模型进行介绍,分析SIL验证过程中可能存在的不确定性类型;然后针对参数不确定性中概率分布已知和未知这两种类型,分别采用蒙特卡洛法和模糊理论构建了硬件SIL的验证模型,并从三种测度角度对基于模糊理论得出的结果进行评价,同时从符合性概率角度对两种方法得出的结果进行比较;最后以某实际1oo2结构的铁路信号安全计算机为例对所提出的方法进行了仿真验证,证明了该方法的有效性。
1 铁路信号安全计算机硬件SIL验证模型及不确定性类型
1.1 常见硬件冗余结构及SIL验证模型
以MooN(M≤N)表示在N个独立完成相同功能通道中的M个通道(系统功能完好的条件为N个通道中有M个及M以上个完好),铁路信号安全计算机常见的双机热备、二取二和三取二冗余,可分别表示为1oo2,2oo2和2oo3[19]。图1为IEC 61508给出的三种冗余方式的结构图及对应的可靠性框图。
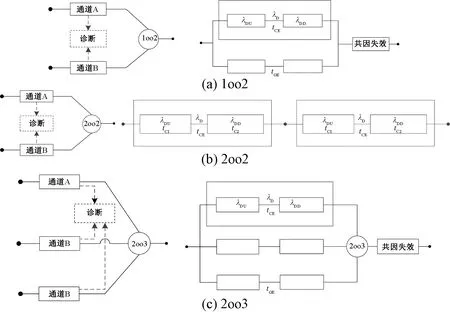
图1 冗余结构可靠性框图
IEC 61508-6中提供的上述结构中每小时危险失效概率PFH的计算公式为其硬件SIL的验证模型[5],即
PFH1oo2=2[(1-β)λDU+
(1-βD)λDD](1-β)λDUtCE+βλDU
( 1 )
PFH2oo2=2λDU
( 2 )
PFH2oo3=6[(1-β)λDU+
(1-βD)λDD](1-β)λDUtCE+βλDU
( 3 )
式中:tCE=(1-DC)(0.5T+MRT)+DC·MTTR为等效平均停止工作时间;DC为诊断覆盖率;MRT为平均维修时间;MTTR为平均恢复时间,当忽略故障检测时间时,MRT=MTTR;λDD=λDDC为可被在线检测到的危险失效率;λDU=λD(1-DC)为不能被在线检测到的危险失效率;λD为危险失效率;β和βD分别为无法检测和可检测的共因失效分数;T为检验测试时间间隔。
1.2 硬件SIL验证中的不确定性类型分析
对于铁路信号安全计算机这类现代高可靠可编程电子设备来说,由于失效次数较少,现场失效数据统计不足,因此不容易捕获到失效参数的精确概率[20]。而评估人员在SIL验证中通常假定器件的失效参数已经准确获得,即定义为精确数值,但这时选取的参数只是其中一个工作条件点处的值,忽略了不确定性因素的影响,由此得到的SIL验证结果实际上只是关于这个点的精确值,这导致SIL验证中对分析验证人员经验的强烈依赖,使得最终验证结果的可信度不高,从而可能增加做出错误决策的风险[21]。
针对硬件SIL验证中的不确定性,IEC 61508在其最新版本中给出了结构约束的路线2,该路线增加了SIL定量评估中对可靠性数据不确定性分析的要求,也增加了对结果置信度的要求,但标准中却没有给出具体可参照或执行的步骤与方法[22]。
鉴于此,首先对SIL验证中存在的不确定性类型进行分析,为之后选择不同的方法处理奠定基础。本文从不确定性因素的来源将其分为模型不确定性、参数不确定性和人为引入不确定性三类[23]。其中模型不确定性是在最初建立数学模型时,由概念和数学模型不能精确描述现实而引起的不确定性(如一些研究在分析冗余系统的安全性时假设系统中各部件相互独立,未考虑共因失效);参数不确定性是由模型中不能得到精确参数而引起的不确定性[18];人为引入不确定性指技术人员在进行分析评估时由于理解能力差异等造成的不确定性。在硬件SIL验证中,由于失效数据不够充分、可靠性试验不足或存在专家经验等主观因素,导致λD,DC,β,βD,MTTR,MRT等参数通常难以获得质量较高的数据,因此“参数不确定性”成为了硬件SIL验证中最容易产生且最为重要的一类不确定性问题。本文主要对这类不确定性进行分析,根据已知参数信息量的多少,可将参数不确定性问题大致分为表1中的三类[14]。

表1 硬件SIL验证中的参数不确定性类型
如表1所示,针对参数概率分布已知的“部分信息”类型,拟采用蒙特卡洛法进行仿真模拟;而针对参数概率分布未知的“极少信息”类型,拟采用模糊理论进行分析。此外,为有效区分参数不确定导致的结果分布于多个SIL区间的现象,根据表2所示的IEC 61508中高要求或连续操作模式下安全功能目标失效量对应SIL的划分标准,定义每个级别SIL对应PFH量值的上限为SILRU,得到如表3所示的划分范围。

表2 高要求或连续操作模式下安全功能目标失效量对应SIL

表3 SILRU对应量值及等级
2 参数概率分布已知下的硬件SIL验证
2.1 蒙特卡洛法
蒙特卡洛法(Monte Carlo Analysis,MCA)又称概率模拟方法,它以概率论、随机过程和数理统计为理论基础,是基于给定参数概率密度函数的一种随机抽样方法,可用于对参数满足某种概率分布的问题进行研究。其基本思想是:针对待求问题,根据物理现象本身的统计规律或人为构造合适的依赖随机变量的概率模型,使某些随机变量的统计量为待求问题的解,通过对大量模拟仿真试验(大统计量的统计实验方法或计算机随机模拟方法)结果的分析来计算所求参数,得出实际问题的近似解。和确定性方法的计算结果不同,采用MCA得到的是输出结果的分布区间,这在一定程度上比不考虑不确定因素,仅用单一值来描述输出结果更加全面准确。该方法能够比较逼真地描述具有随机性质的事物特点及物理实验过程,且与所求解问题的几何维数关系不大,甚至几何越复杂,其优点越明显[15]。此外,实现该方法的程序结构简单,所需存贮单元比其他数值方法少,容易使用个人计算机编写通用性很强的应用软件。
2.2 基于MCA的硬件SIL验证
根据2.1节MCA基本思想的介绍,提出基于MCA的铁路信号安全计算机硬件SIL验证步骤Step1~Step5,其中Step5改变了以往对结果的分布区间进行判定评估以得到最终结论的方式,采用以95%的置信度判定系统所满足的SIL等级,以此满足结构约束中有关结果置信度的要求,使结果更加可信。
Step1根据每个输入参数所服从的概率分布(一般有Uniform分布,Normal分布,Beta分布,Lognormal分布,Gamma分布等),在仿真软件中使用随机数生成一组输入参数的随机值。
Step2将Step1生成的一组随机值代入相应的SIL验证模型中得到输出结果y(PFH)。
Step3重复执行Step1和Step2,直到产生n个独立的输出结果。
Step4从获得的样本中生成输出结果的统计数据,如最大值、最小值、均值等。
Step5根据95%的置信度来判定计算得到的y(PFH)值是否包含在所需SILRU内,若样本值满足
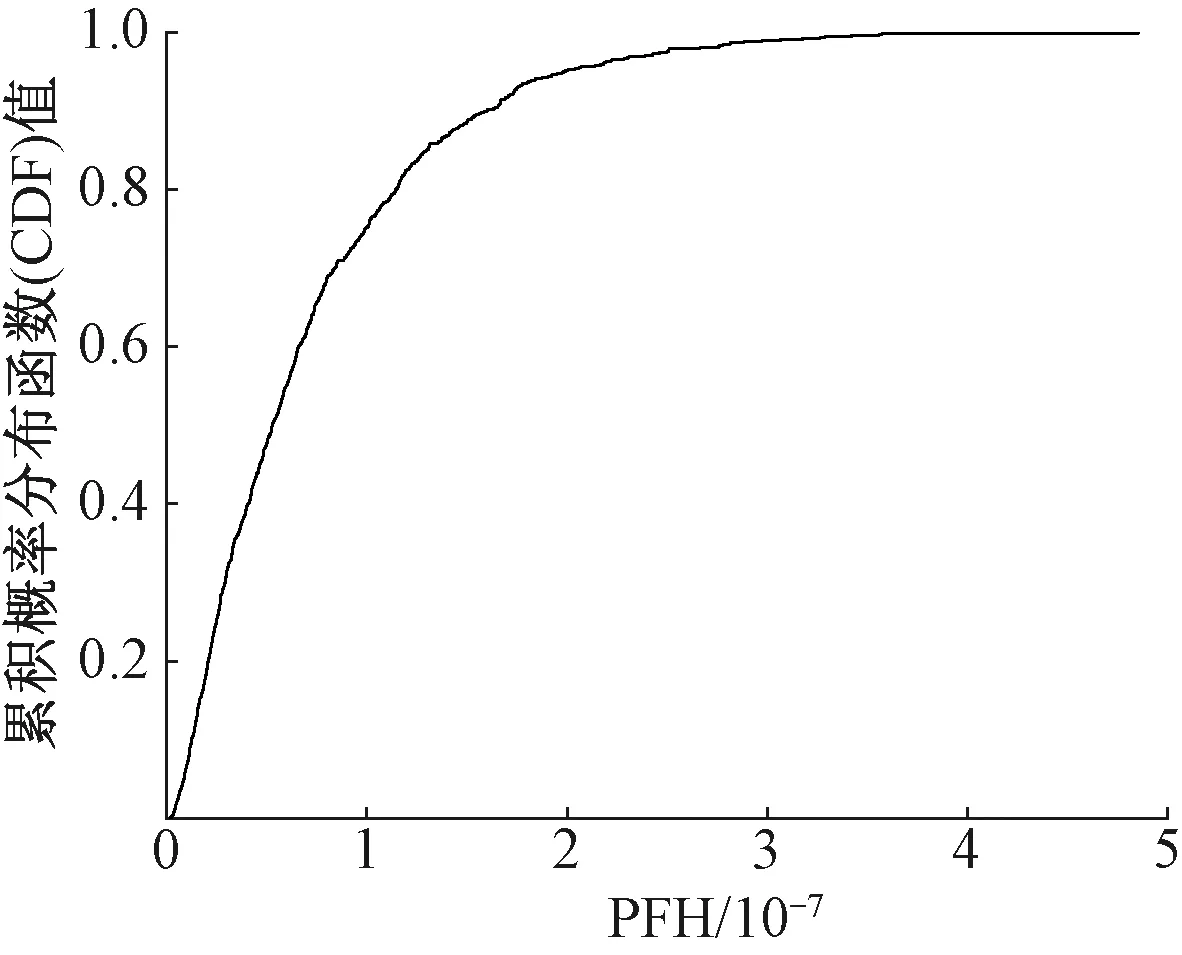
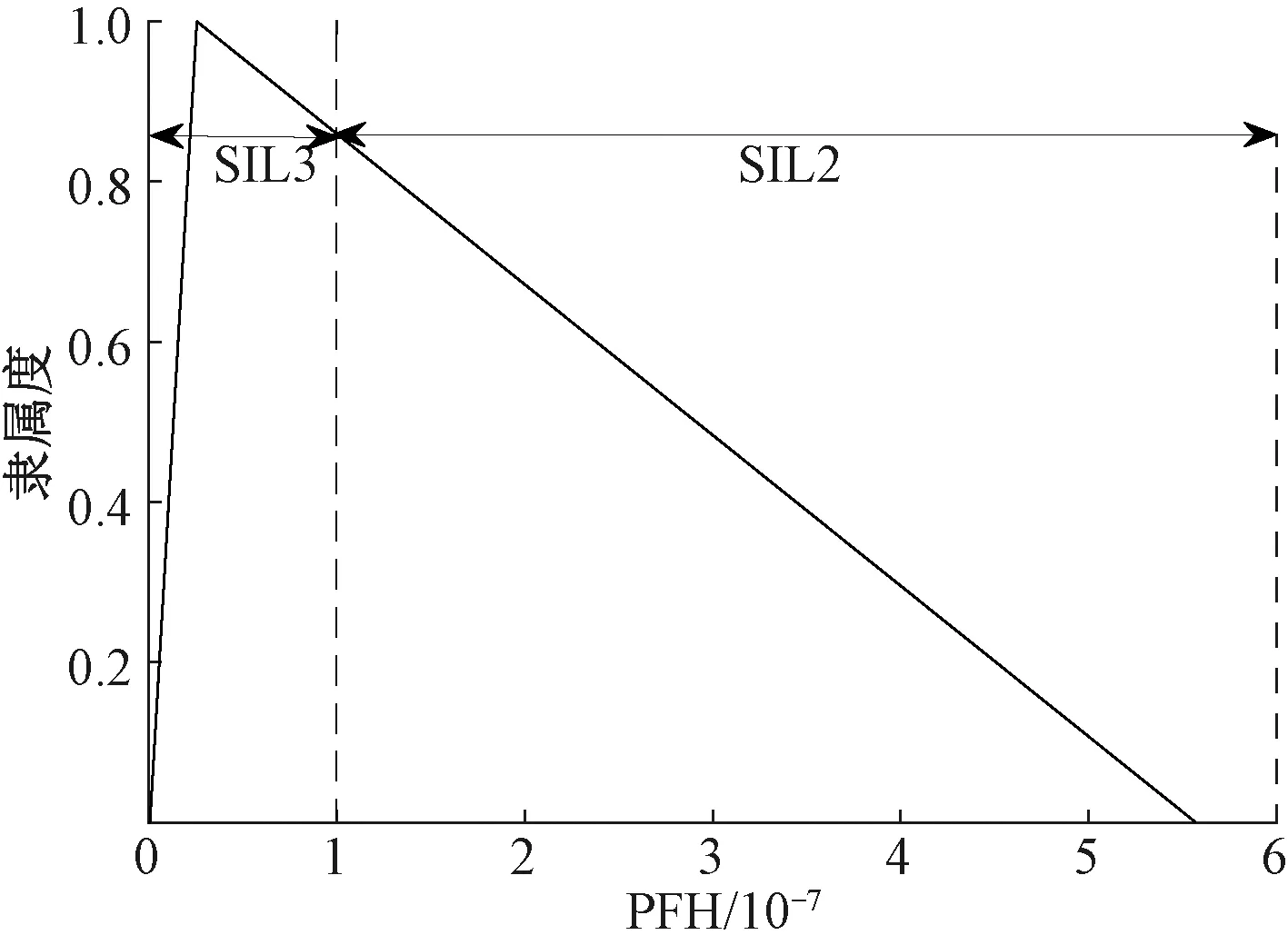
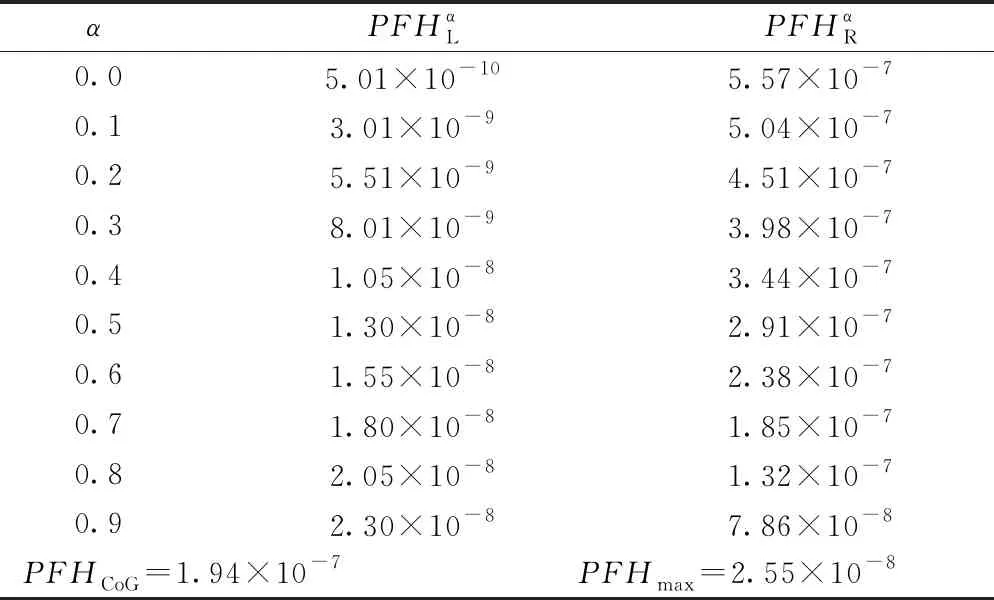
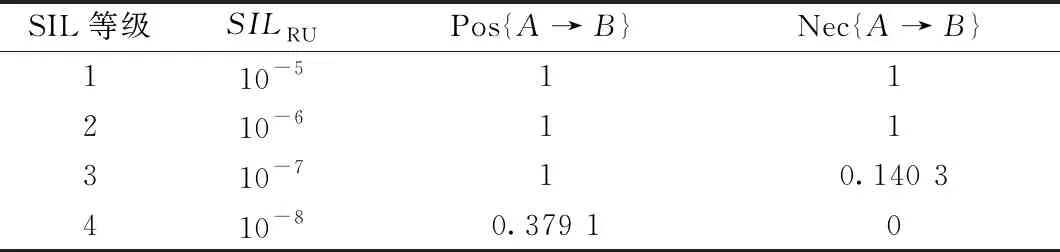
P(y ( 4 ) 则表示安全完整性等级可达到SILRU对应的SIL等级(采用表3进行判定)。式(4)中,P表示累积概率分布函数。基本流程见图2。 图2 基于MCA的铁路信号安全计算机硬件SIL验证流程 根据概率论相关理论知识,当仿真次数n趋于无穷大时,随机变量的算术平均值将近似等于它的数学期望,即只要n取到足够大,便可逼近所求的真实解,使评估结果更加可靠,因此可通过增加抽样次数来提高结果的精度,保证统计数据的稳定性。为保证样本充足,本文在计算机性能允许的范围内取n=105。 采用2.2节基于MCA的硬件SIL验证方法分析某1oo2结构的安全计算机。各参数取值如表4所示。其中λD服从三角分布,上下边界选取IEC 61508-6在计算冗余结构的PFH时提供的算例表中λD的取值范围:0.5×10-7~2.5×10-5,其最可能取值(即众数)为参考文献[24]中推荐的典型值5×10-6。对于DC,IEC 61508-6算例表中推荐的取值点为0、60%、90%、99%,但考虑铁路信号安全计算机属于高可靠设备,文献[4,25-27]等研究铁路信号设备安全性相关的文献中均指定DC∈(0.90,0.99),故本例亦取DC为0.90~0.99并服从均匀分布(为使其取值在相同长度间隔的分布概率为等可能);对于β和βD,鉴于难以获取共因失效有关数据,故取标准中推荐的最大范围,即β为0.02~0.20、βD为0.01~0.10,且同样服从均匀分布;对于MRT与MTTR,由维护人员决定,通常固定不变,均取标准中推荐的值:8 h;对于T,铁路信号设备通常执行半年检或年检(如文献[12]推荐计算机联锁系统的检验测试周期为一年),这里取IEC 61508-6中针对高要求操作模式的系统所推荐的最长时间间隔1 a(8 760 h)。 表4 各参数取值 将表4参数代入1oo2结构的SIL验证模型(即式(1)中)进行仿真,得到输出结果的统计指标如表5所示,其中ymin、ymax、ymean分别表示结果的最小值、最大值和均值。样本累计概率分布函数见图3。 表5 MCA模拟下1oo2结构PFH相关指标输出结果 图3 输出样本累计概率分布函数 由表5可知,输出结果的均值6.77×10-8与各参数取单一固定值(取表4中各参数取值范围的均值作为参数的固定值)计算得到的结果(3.08×10-8)属于同一个数量级,均对应SIL3。但按照式(4)在图3中进行验证可得:P(y<2.08×10-7)=0.95,这表明结果有95%的可能性满足SIL2,这与前述结论相差一个等级。且若使系统满足其他安全完整性等级,可得表6所示结果在不同SIL的置信度。 表6 输出结果符合相关SIL的概率 由表6可得,P(y<10-5)=P(y<10-6)=1,即满足SIL2的可能性为100%;P(y<10-7)=0.76,即有76%的可能性满足SIL3;P(y<10-8)=0.07,即有7%的可能性满足SIL4。可以看出,考虑参数不确定性的结果根据不同的概率值分布在不同的等级范围内,这表明若输入的参数存在不确定性,那么不同时刻或不同批次的输出结果也有差异,必须对该差异,即输出区间进行考察评定,才能从安全评估的角度给出合理的评估结果,因此这种形式的描述方式比单一确定值表示的结果更具意义。 第2节对参数不确定性中概率分布已知的情况做了分析,但多数情况下参数可获取的信息极少,为此本节利用模糊理论(FT)中的有关方法对参数概率分布未知的情况进行分析。 定义1:在论域U上,存在映射为 ( 5 ) Aα={u|u∈U,A(u)≥α} ( 6 ) 图4 α截集下模糊集的支集与核 有研究表明,在系统安全性分析中,参数的隶属函数常由梯形、三角形等模糊数定义[28],且梯形模糊数(三角模糊数是特殊的梯形模糊数)是一种线性分布函数,其外形直观、代数计算简洁[29]。因此这里采用梯形模糊数描述各参数的不确定性,其隶属函数表达式如下 ( 7 ) 隶属函数见图5。 图5 梯形模糊数的隶属函数 ( 8 ) 参数经模糊代数运算后的结果为一模糊数,解模糊化是将该结果转换成一个单一的清晰值,该数值表示所估计模糊变量中最可能的值。解模糊法包括加权平均法、最大隶属度法、最大平均值法、重心法等。这里对最常用的重心法(Center of Gravity,CoG)、最大隶属度法(Maximum Membership,MM)进行介绍。 定义5:最大隶属度法是取模糊数在截集α=1处的值,即 ( 9 ) 定义6:重心法又称面积中心法或质心法,该指标考虑了模糊数的整体变化,即[31] (10) 根据3.1节对模糊理论有关概念的介绍,本节提出基于FT的铁路信号安全计算机硬件SIL验证方法,其基本思路是:首先确定各参数的模糊数取值,然后代入目标系统的SIL验证模型(即1.1节中给出的PFH计算公式)中,接着通过模糊运算得到模糊数形式的结果,最后对结果进行评估,判定所满足的SIL等级。该方法的重点是如何对结果进行评估,传统方式是根据不同水平的α截集计算得到结果的左右区间边界,以此判断系统满足的SIL;或通过重心法、最大隶属度法等对结果解模糊化得到其清晰值,从而判断满足的SIL。但该方式存在如下问题:①即使α=0时结果的取值范围最为保守,但实际中能达到α=0的情况可能并不常见;②如果取最高隶属度α=1,那么就忽略了结果的不确定性,为了避免这种情况,分析人员通常选择其他任意值的水平截集(如0.9、0.8等),但这会导致α取值的主观性,即在计算中人为二次引入了不确定性;③虽然重心法去模糊化后的结果更符合实际,但该指标并不包含置信度,即并未像MCA一样从置信度的角度对结果进行评判,因此可信程度无从得知。基于以上原因,本节提出从置信度的角度对计算出的模糊结果所满足的SIL进行评价。 (1)测度理论 采用Zadeh提出的可能性测度及必然性测度[32]来评估命题“计算得到的PFH小于等于SILRU”。首先定义两个模糊子集A和B,其中A中元素表示利用SIL验证公式计算获得的PFH模糊数,B中元素表示小于等于SILRU的值,给出可能性测度Pos{A→B}与必然性测度Nec{A→B}示意图,见图6,其表达式为 图6 可能性测度及必然性测度 (11) 式中:Sup表示集合最小的上界;Inf表示集合最大的下界。 由图6可知,可能性测度度量了元素u同属于A和B的最大程度,其取决于两个模糊子集A、B相交点的高度;而必然性测度度量了B包含A的程度。两个测度可以理解为模糊事件“PFH取值小于等于SILRU”发生概率的上限和下限。事实上,基于可能性测度可理解为秉持着乐观积极的态度去解决问题,结果更倾向模糊事件的发生,而基于必然性测度可理解为秉持着悲观消极的态度去解决问题,结果更倾向模糊事件的不发生,但这并不意味着一个模糊事件的可能性为1,该事件就一定成立,另一方面,一个模糊事件的必然性为0也并不意味着该事件一定不成立。鉴于可能性测度与必然性测度间存在的矛盾,引入文献[33]提出的可信性测度Cr,其定义为 (12) 由式(12)可以看出,可信性测度中和了可能性测度与必然性测度,采取基于二者平均值的一种中间态度。假如一个模糊事件的可信性为1,则该事件必然成立;反之,若一个模糊事件的可信性为0,则该事件必然不成立[34]。 (2)符合性概率 该指标利用对模糊数隶属函数的积分,验证结果与SILRU的符合概率。定义计算得到的结果PFH(事件A)小于等于SILRU(事件B)的概率为PF,符合性概率示意见图7,其计算式为 图7 符合性概率示意 (13) 为了与采用MCA仿真得到的结果作比较,本节依旧对1oo2结构的系统进行分析,各参数模糊数取值如表7所示,采用安全性分析中最常用的梯形模糊数,其中模糊区间上下限与表4的取值相同。在计算机中仿真得到输出结果的隶属函数见图8,给出不同α截集下输出结果的左右区间数如表8所示。 表7 各参数取值 图8 输出结果的隶属函数 表8 不同α截集对应左右区间数 由图8及表8可知,采用模糊数计算得到PFH的支集即PFH(α=0)=(5.01×10-10,5.57×10-7)比采用MCA得到的极限值(1.42×10-9,4.46×10-7)的区间范围要宽;采用最大隶属度法解模糊化得到的值2.55×10-8与采用MCA求得的均值6.77×10-8非常接近,而最大隶属度得到的值即是隶属度为1处所取的值,即忽略了参数不确定性的非保守值。由此可见,与MCA相比,模糊数提供了更为宽泛的不确定性,更适合处理存在高度不确定性的问题,这在验证包含极少信息的系统的安全完整性等级时更有参考意义。此外,在仿真软件中采用MCA完成本节提供的例子耗时0.746 s,而采用模糊理论仅耗时0.007 s,相差达100倍,这意味着采用模糊理论得到结果边界的用时更短。 根据表6中的参数,采用式(11)求解得出结果的可能性测度和必然性测度如表9所示。 表9 可能性测度与必然性测度计算结果 由表9可知,结果满足SIL2的可能性测度和必然性测度均为1;满足SIL3的可能性测度为1而必然性为0.140 3;满足SIL4的可能性测度为0.379 1而必然性为0.140 3。可以看出,必然性测度的结果较可能性测度更为保守,符合3.2节对两种测度的描述。然后采用式(12)计算结果的可信性测度如表10所示。 表10 可信性测度计算结果 由表10可知,从可信性测度分析,结果所能声明的最大安全完整性等级为2级。 最后,将前述计算得到的结果代入式(13)得到结果的符合性概率,并与第2节采用MCA求得的不同SIL下的概率进行对比,结果如表11所示。 表11 符合性概率计算结果及与采用MCA计算结果的对比 由表可知,从符合性概率角度来看,基于FT所能声明的最大SIL等级与基于MCA相同,均为SIL2。而结果符合SIL3、SIL4的概率值有:PF(A≤10-7) 针对铁路信号安全计算机硬件SIL验证中存在的参数不确定性问题,首先采用蒙特卡洛法分析了参数概率分布已知类型的不确定性,然后利用模糊理论对参数概率分布未知类型的不确定性进行分析,并从三种测度和符合性概率角度对利用模糊理论得到的结果进行评价,同时与基于蒙特卡洛法得到的结果进行比较。结果表明: (1)采用模糊理论计算得到的模糊数在截集α=0处的支集(最不确定性区间)包含了采用MCA抽样得到的概率分布的上下界,这表明模糊理论更加保守。从可信性测度和符合性概率角度来看,基于模糊理论得到的结果所能声明的最大安全完整性等级均与基于MCA得到的结果一致,且前者计算过程耗时更短。 (2)考虑参数不确定性的输出结果根据不同的概率值、测度值提供了不同等级的安全完整性,这比采用固定参数值输出的单一精确结果更具意义。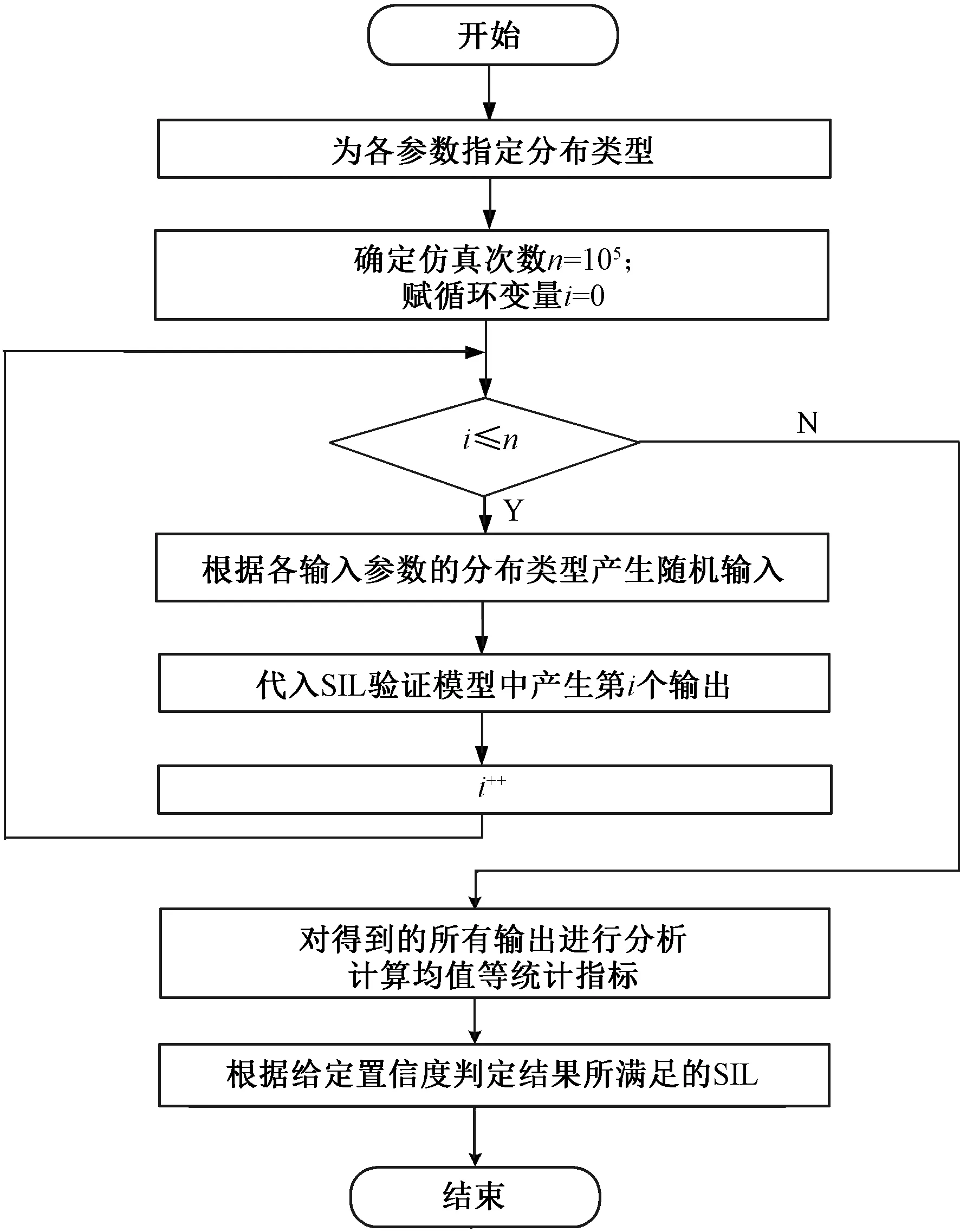
2.3 算例分析



3 参数概率分布未知下的硬件SIL验证
3.1 模糊理论
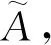
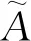
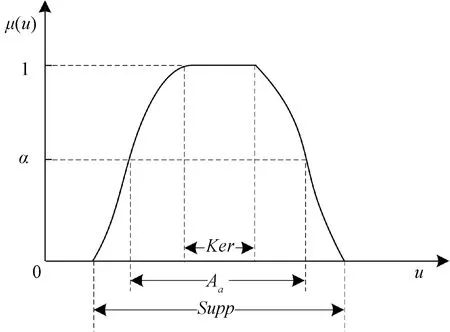
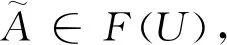
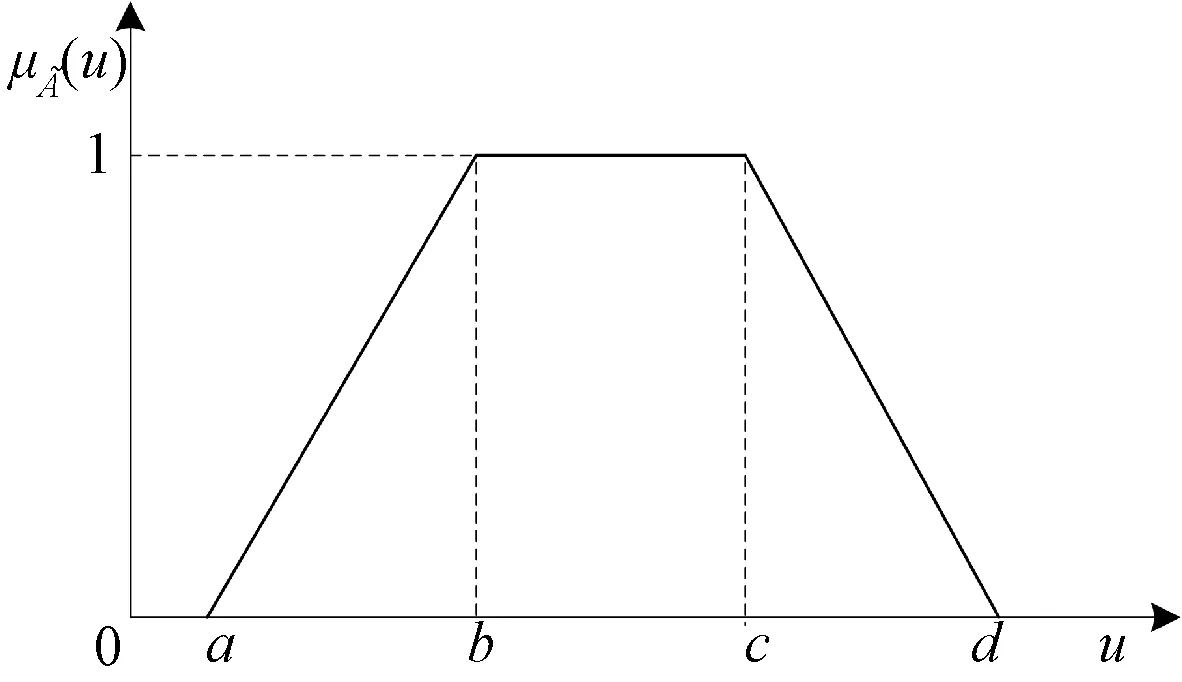
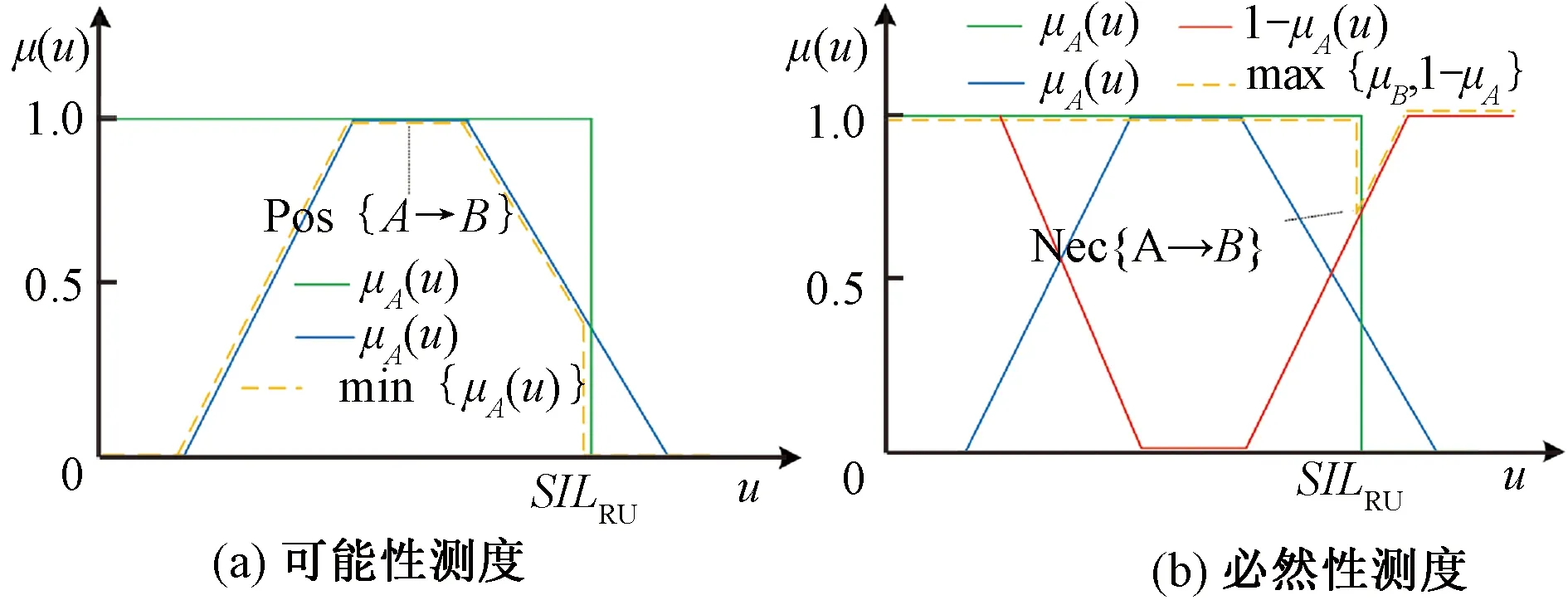
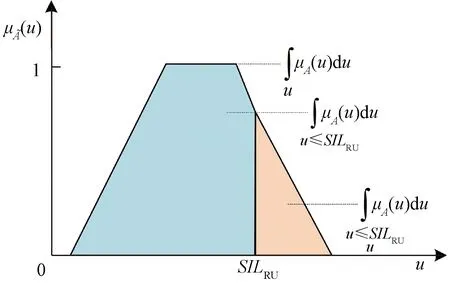
3.2 基于FT的硬件SIL验证
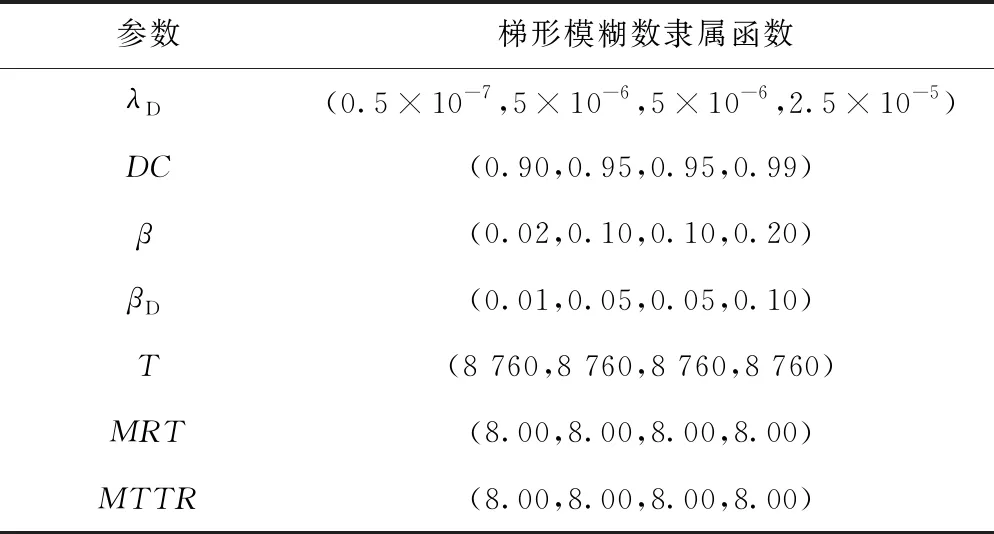
3.3 算例分析


4 结论

