弹性离散支撑钢轨的振动和声辐射特性研究

刘清源，成 功,2，何远鹏，陈宗平，韩 健，圣小珍

(1.西南交通大学 牵引动力国家重点实验室，四川 成都 610031；2.华东交通大学 轨道交通基础设施性能监测与保障国家重点实验室，江西 南昌 330013；3.西南交通大学 机械工程学院，四川 成都 610031；4.上海工程技术大学 城市轨道交通学院, 上海 201620)

随着轨道交通的快速发展，铁路噪声与振动问题受到了社会的广泛关注，钢轨辐射噪声作为铁路噪声的主要来源之一，其振动和声辐射特性的建模和预测也受到了学界的广泛关注。

Remington[1]在建立的轮轨噪声预测模型中使用连续弹性支撑的欧拉梁模型模拟钢轨，Thompson[2]在Remington的基础上，使用离散弹性支撑的铁木辛柯梁模型模拟钢轨，并将其纳入TWINS软件。由于简单的铁木辛柯梁模型在2 000 Hz以上的高频已不再适用，Wu等[3]提出一种采用双层铁木辛柯梁模拟钢轨的方法，与单梁模型相比，双层梁模型能反映高频激励下的截面内变形。Knothe等[4]采用梁模型模拟轨头和轨底、板模型模拟轨腰，使用梁和板的组合模型得到钢轨高频响应。万淑敏等[5]建立离散弹性支撑的三维实体有限元钢轨模型，并得到钢轨的声辐射效率。

Remington[1]的噪声预测模型把钢轨作为线声源处理，根据钢轨的声辐射效率和振动速度计算钢轨的辐射声功率。为了获得高频声辐射，罗斌等[6]使用统计能量分析得到钢轨的1/3倍频程辐射噪声。Sheng等[7-8]基于傅里叶变换，提出一种基于波数域的方法，求解周期性结构在移动和静止谐载荷作用下的响应，并使用2.5维边界元法得到钢轨在移动和静止谐载荷下的声辐射特性。Thompson[9]总结了钢轨噪声和轨道衰减率的关系式，根据钢轨截面的辐射效率和振动衰减率，计算无限长钢轨的辐射声功率。

研究钢轨辐射分为两步，计算钢轨振动和计算钢轨辐射。计算钢轨振动一般采用解析法或者有限元法，可根据需要视钢轨为梁单元模型、多层梁单元模型或者实体单元模型；计算钢轨声辐射主要采用声学边界元法。二维边界元法忽略了振动沿轨道方向的变化，与实际情况相去甚远，但其算出的钢轨辐射效率可结合轨道衰减率计算钢轨噪声。三维边界元受模型网格的影响很大，网格过密会造成计算效率过低，网格过疏会导致模型在高频段的计算结果可信度降低，对研究无限长钢轨的振动特性产生限制。钢轨可以视作在一个方向上无限长的同质、均匀且横截面形状不变的波导体，利用这一特点可以使用于计算钢轨声辐射的三维边界积分方程得到简化。通过将无限长方向的空间变量从空间域变换到波数域，就可以实现在波数域中解耦求解，这就是2.5维边界元法。应用这种方法计算钢轨的声辐射可以克服以上两种模型的缺点，在准确反映振动沿钢轨传播的同时提高计算效率[7-8]。

为了探究基于不同模型和方法所计算出的振动和声辐射特性的差异及其原因，确定它们的适用范围，为研究钢轨振动和声辐射提供参考，并分析刚性轨道板对钢轨辐射声功率的影响，本文采用三种钢轨模型计算无限长钢轨在静止和移动谐载荷下的振动特性和轨道衰减率，并使用2.5维声学边界元方法和衰减率与噪声之间的关系公式计算无限长钢轨在静止谐载荷下的辐射声功率级，并考虑刚性轨道板的影响。

1 钢轨声振模型建立

1.1 钢轨振动模型的建立

本文建立的轨道模型包括UIC60钢轨及轨下扣件系统，其中扣件系统模拟为结构阻尼弹簧，钢轨分别模拟为有限长铁木辛柯梁单元、有限长三维实体单元-铁木辛柯梁单元组合结构及无限长铁木辛柯梁，轨道结构如图1所示。

图1 轨道结构

前两种结构都是有限长结构，长度为210 m。值得注意的是，第二种模拟方法是在21 m长的三维实体有限元钢轨两端分别连接一段梁单元钢轨，一方面可以更准确地得到钢轨的振动特性，另一方面在兼顾计算效率的同时尽量减小截断边界的反射效应。该方法在Ansys中进行模拟，在梁单元和实体单元之间使用多点约束(MPC)连接，如图2所示。其原理是将连接截面处的梁单元节点和实体单元节点的自由度进行刚性连接，用于耦合单元之间的载荷传递。

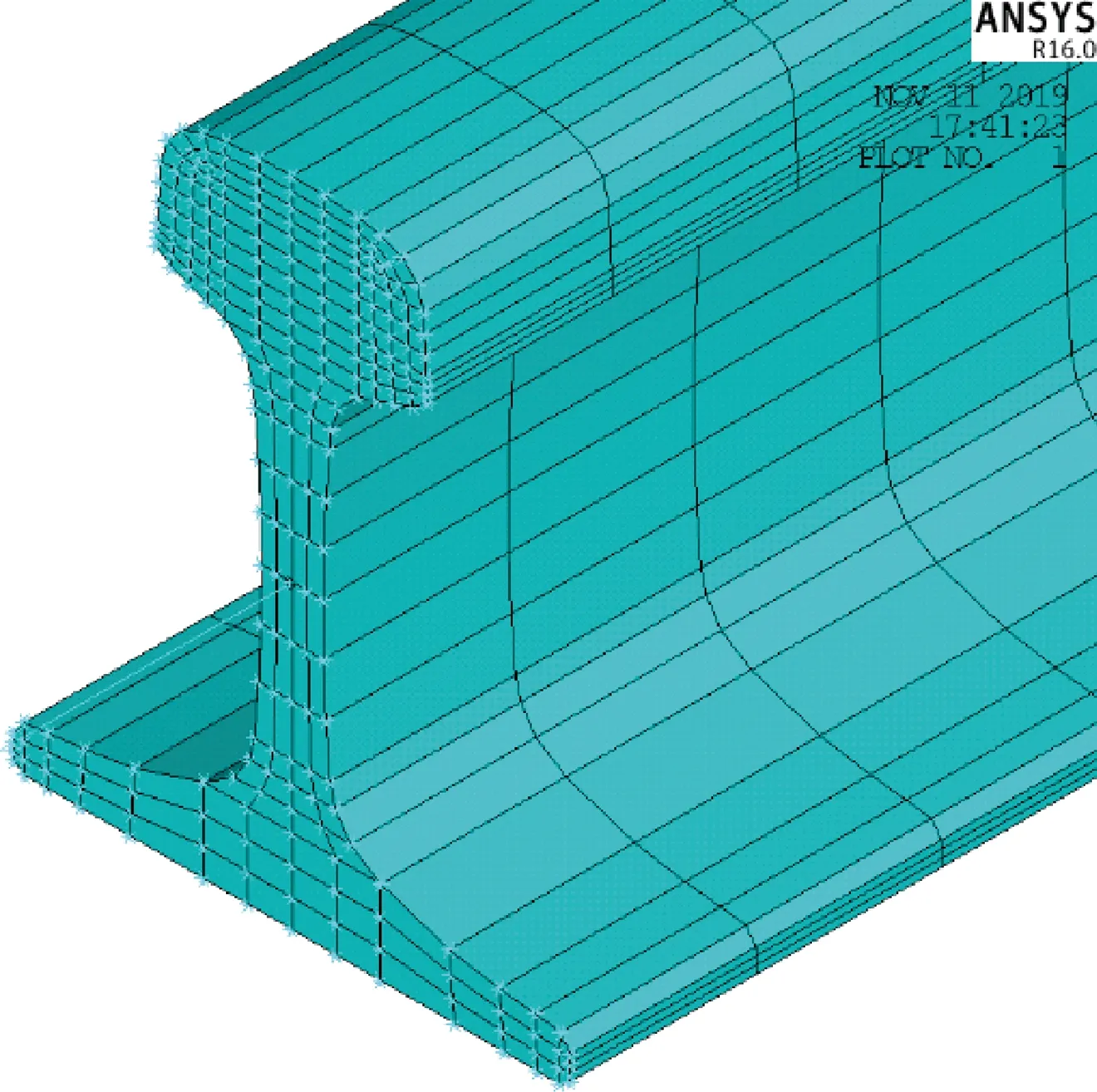
图2 MPC连接实体单元和梁单元

值得注意的是，要研究无限长钢轨的振动和声辐射特性，需要探究多长的有限元模型能够满足要求。本文使用不同长度铁木辛柯梁模型，将端部导纳与原点导纳的比值作为衡量标准，如图3所示。

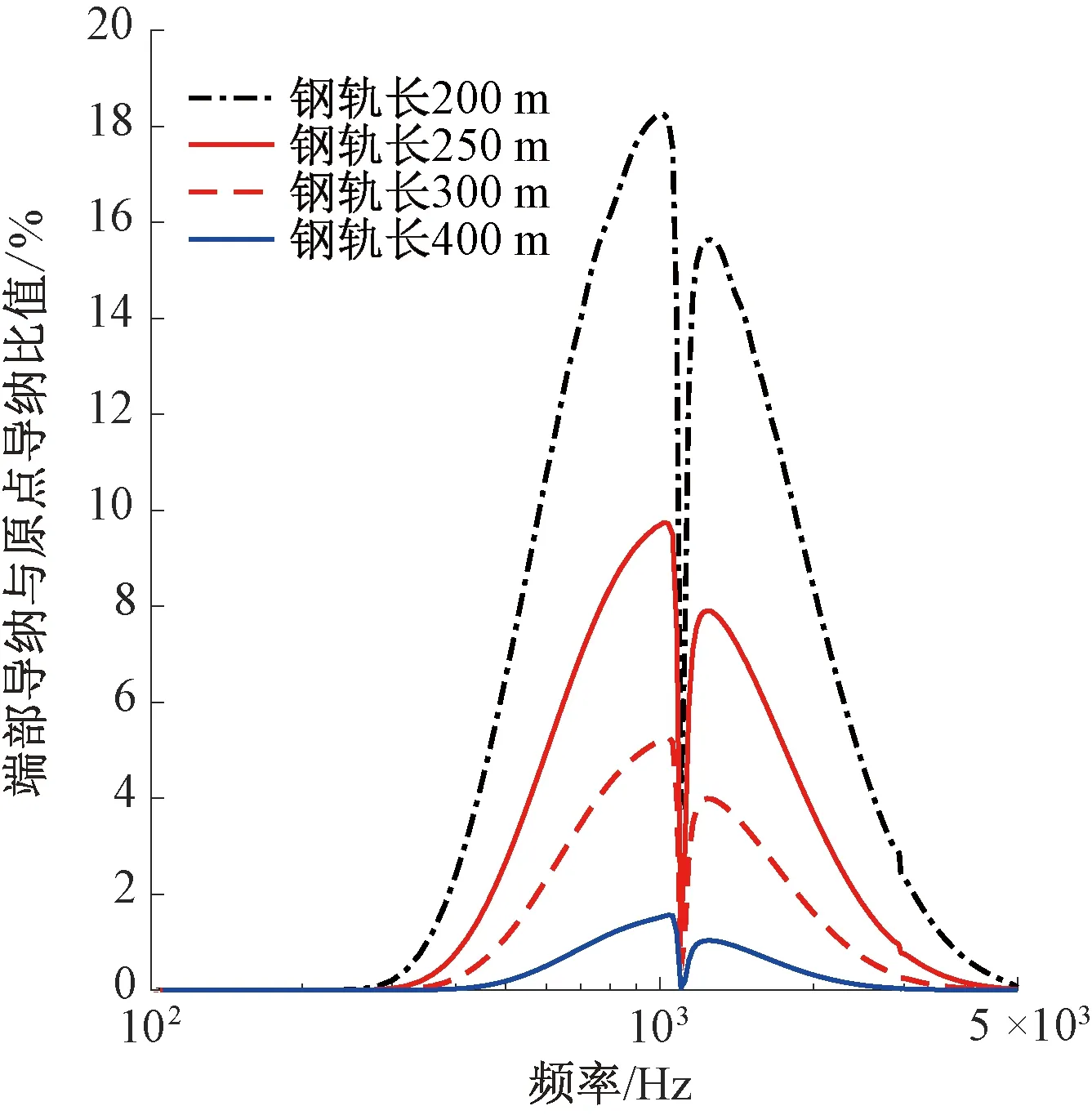
图3 不同长度钢轨端部与原点导纳比值

从图3可以看出，较大的比值出现在400～3 000 Hz。随着钢轨长度的增加，钢轨端部导纳减小，当钢轨长度为200 m时，导纳比值最大不超过20%，此时得到的原点导纳与后文采用的无限长铁木辛柯梁的计算结果基本一致，且不会出现因截断边界反射产生的波动，所以导纳比值不超过20%时(即相差14 dB)可以将有限长的钢轨近似为无限长钢轨。

第三种结构是将钢轨模拟为一根无限长的铁木辛柯梁，该梁在周期性的扣件位置被离散支撑，其钢轨在单位高速移动谐载荷作用下的速度振动响应(t=0)可以写为[8]

(1)

1.2 钢轨声辐射计算方法

Thompson[9]对无限长钢轨的声功率计算公式进行了简化，得到声功率级与轨道衰减率之间的关系式为

(2)

式中:Wref为参考声功率，Wref=10-12W;vref为参考速度，vref=10-9m/s;σ为辐射效率;ρ0c0为空气特性阻抗;P为钢轨横截面周长;v(0)为激励点处的钢轨速度;δ为轨道衰减率，dB/m。

该声功率计算方法认为钢轨下部的支撑是连续支撑，因此认为其振动衰减率与波数β的虚部成正比，但由式(1)易知离散支撑下的钢轨在每跨不同位置的振动幅值都不相同。因此，本文在文献[7]和文献[8]的基础上将无限长铁木辛柯梁钢轨和2.5维边界元相结合，得到更符合真实情况的钢轨辐射声功率，其计算公式为

(3)

(4)

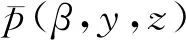
(5)

(6)

式中：K0为修正的0阶第二类贝塞尔函数；k0=2πf/c0,c0为声速，f为频率。

1.3 模型参数的选取

本文只考虑钢轨垂向振动特性和垂向振动的辐射声功率，因此仅设置了轨下垫板的垂向刚度。钢轨和轨下垫板的参数见表1。

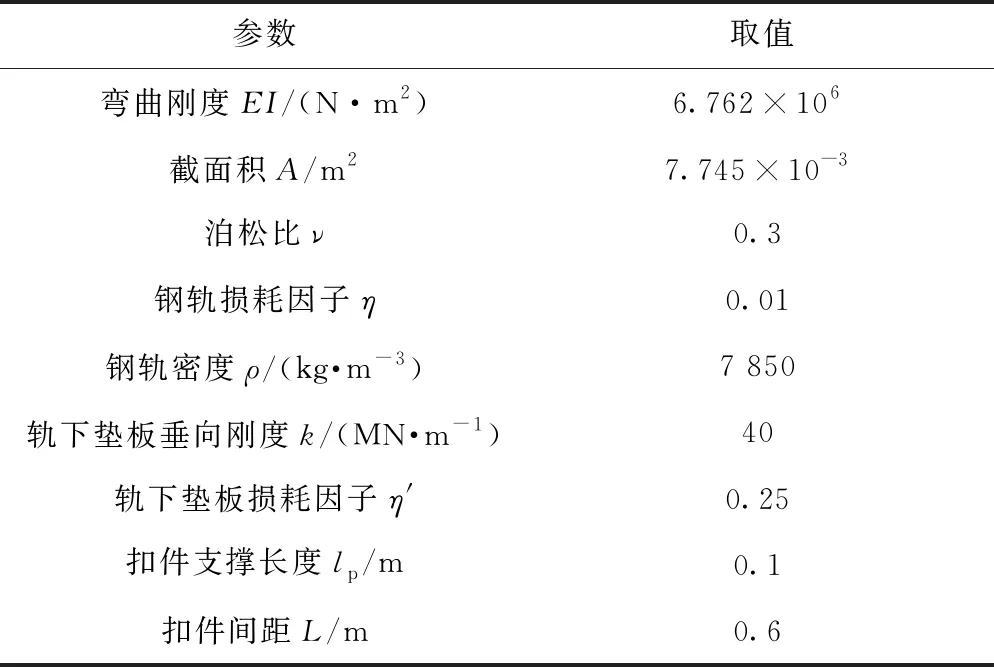
表1 轨道参数

采用梁单元模拟钢轨受力情况与实际情况有差异，梁模型中集中载荷施加在钢轨的中心，弹簧单元实际支撑的位置也是钢轨中心。实体模型受力需要与梁模型受力一致，所以对钢轨截面划分网格时，保证截面中心位置有一个节点，实现对钢轨的中心处施加集中载荷和提供弹簧支撑，如图4所示。

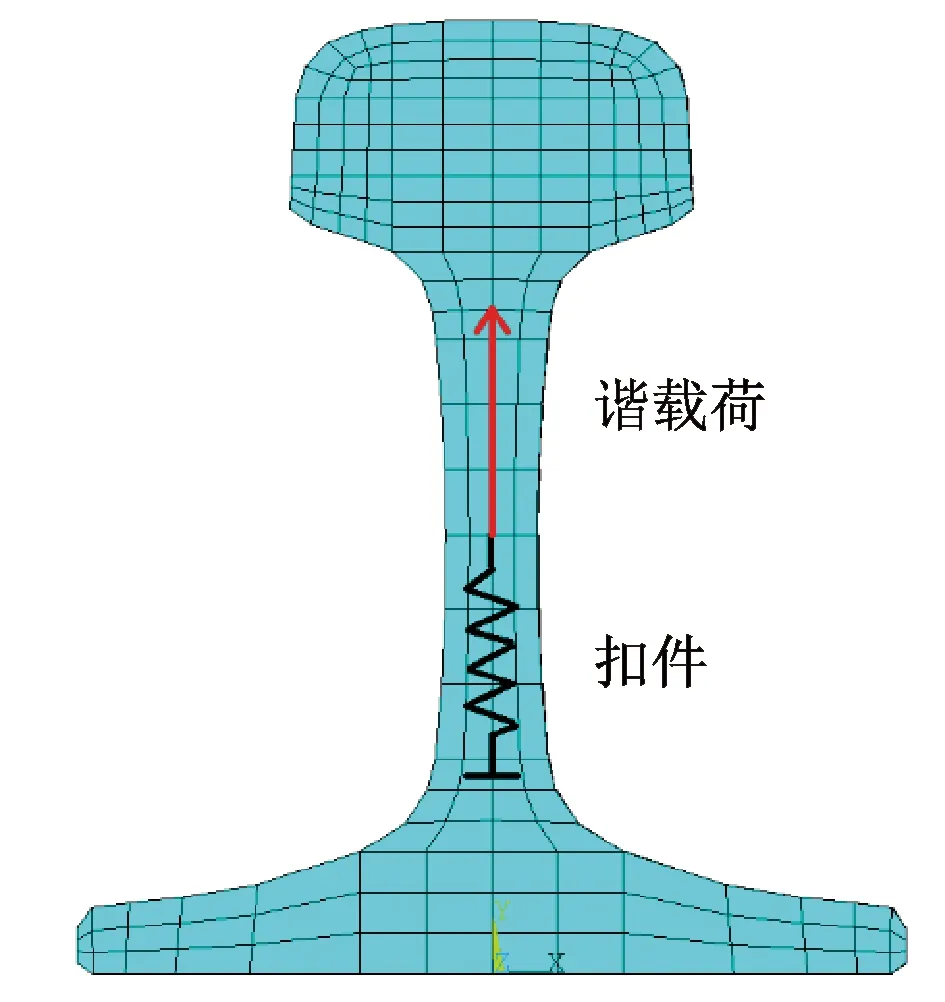
图4 有限元实体模型受力示意

使用有限元法计算钢轨振动和辐射声功率对单元长度有要求，需要单元的最大边长不超过钢轨传递最短波长的1/6。以自由铁木辛柯梁钢轨为例，无限长钢轨弯曲波的频散曲线如图5所示。由于梁模型只能传递弯曲波，因此图5只有一条曲线，但是考虑钢轨的其他传播波(在这些振动波中，钢轨横截面发生变形)在固定频率时的波数要小于弯曲波的波数，当钢轨网格满足弯曲波要求时，这些传播波也天然满足。

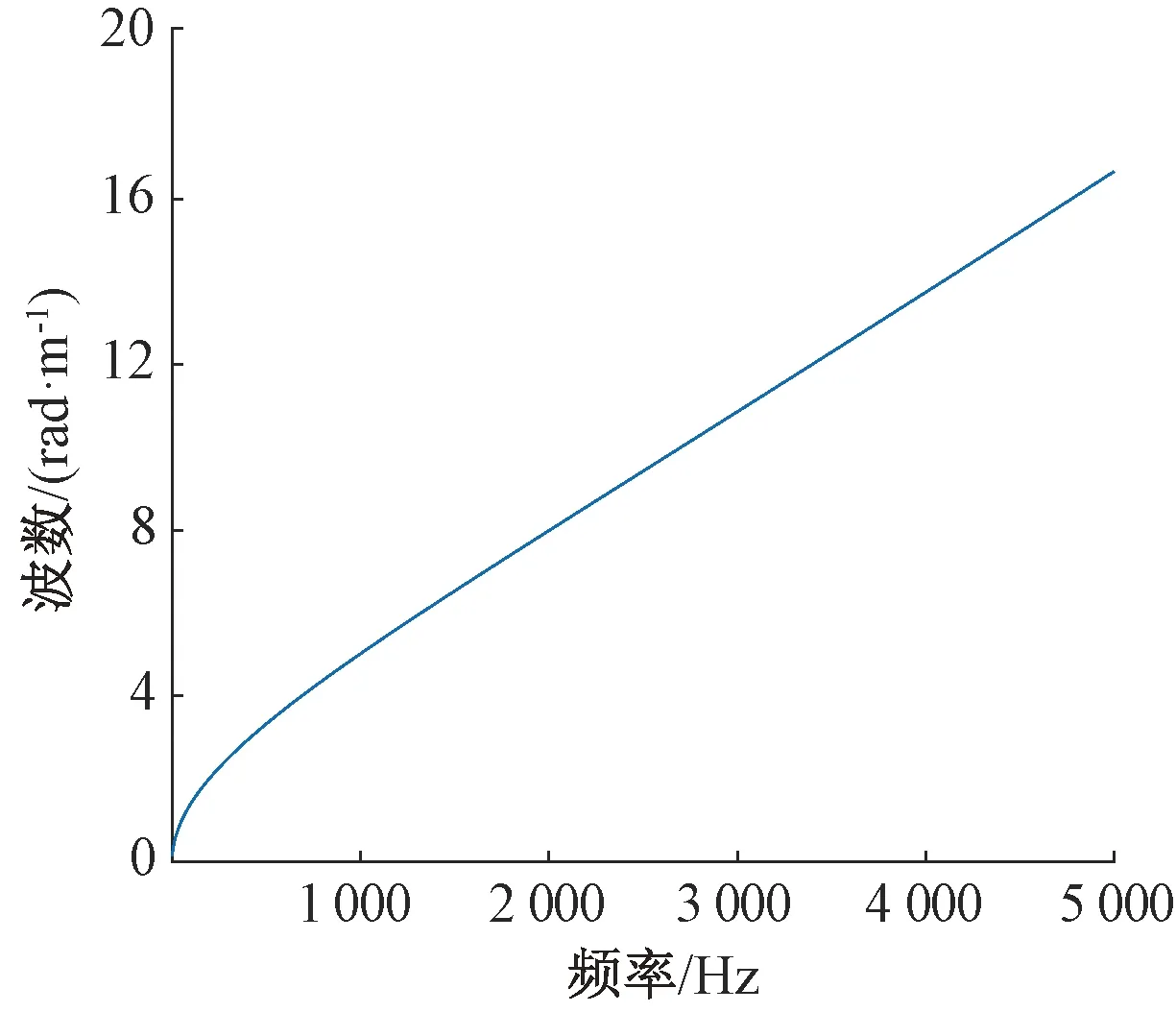
图5 自由钢轨弯曲波频散曲线

2 钢轨垂向原点位移导纳特性分析

原点导纳是研究振动特性的一个常用指标，是结构在单位谐载荷下的响应(位移、速度、加速度)。分别对有限长铁木辛柯梁、有限长三维实体-铁木辛柯梁组合结构及无限长铁木辛柯梁施加单位垂向谐载荷，载荷作用于相邻扣件的跨中位置，载荷频率范围为10～5 000 Hz，步长为10 Hz。对实体-梁组合模型，荷载施加在跨中截面的中心轴处。根据文献[10]，使用有限元法计算实体单元的原点导纳会产生奇异性，本文为避免这种情况，将与激励点相隔一个单元长度(50 mm)的点作为响应点，将该响应点的响应作为原点导纳，得到原点位移导纳如图6所示。

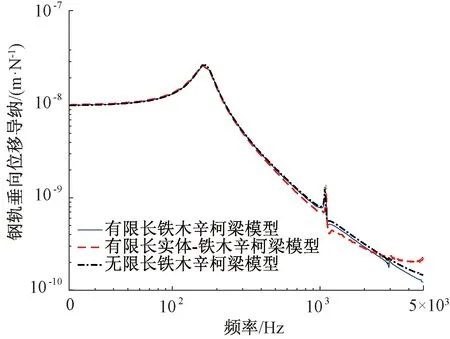
图6 原点位移导纳

图6中，导纳第一个峰值出现在170 Hz，是钢轨整体在扣件上的垂向振动特征频率，是轨道系统的一阶共振频率，其可以计算为

(7)

式中：k为单位长度钢轨的刚度，N/m2；m为单位长度钢轨的质量，kg/m。

更高频率的两个峰值(1 080 Hz和2 940 Hz)对应钢轨的两阶pinned-pinned频率。pinned-pinned频率主要受钢轨弯曲刚度和扣件间距的影响，与扣件支撑钢轨的宽度也有关系但影响不大。在pinned-pinned频率处，当载荷作用在跨中时，原点导纳会出现峰值，作用在扣件上方会出现谷值。

pinned-pinned模态产生的主要原因是驻波效应，即该频率下的半波长等于支撑间距，驻波节点正处于扣件位置。铁木辛柯梁的垂向振动pinned-pinned频率为

(8)

式中：n0为钢轨pinned-pinned模态阶数；L为轨枕间距，m。

通过对比三种模型可以发现：

(1)有限长铁木辛柯梁模型和无限长铁木辛柯梁模型的原点导纳基本保持一致，说明在计算原点导纳时，200 m的有限元梁模型已经可以很好地还原钢轨的无限长特性。

(2)三种模型在频率小于3 000 Hz时的垂向位移导纳基本一致，当频率大于3 000 Hz以后，实体-梁组合模型的垂向位移导纳开始显著大于另外两种梁模型的位移导纳。因为铁木辛柯梁模型的使用需要满足对截面变形的一些假设，受到高频激励后，这些假设不再有效，因此梁的模型已经不再适合。实体-梁模型受到高频载荷作用，钢轨根部发生翘曲，横截面发生变形，不再维持在一个平面，与两个梁模型相比变形也更大。

3 轨道衰减率分析

轨道衰减率是评价钢轨振动纵向传播特性的重要指标，其对钢轨的声辐射至关重要[11]。轨道衰减率代表了振动沿钢轨方向减弱的能力，轨道衰减率大说明该频率下的振动沿钢轨方向传播能力差，轨道系统的动态阻尼大。钢轨的支撑方式和扣件阻尼都对轨道衰减率有很大影响。

工程上通常根据欧洲标准EN 15641：2008+A1：2010[12]计算轨道衰减率，该方法采用移动激励的方式，在不同的位置用力锤进行敲击，测出不同距离的导纳，得到轨道衰减率为

(9)

式中:A(xn)为钢轨原点(0点)施加单位载荷时第n点的导纳函数;A(x0)为在0点施加单位载荷时原点的导纳函数;Δxn为第n个测点到第(n-1)个测点的距离。值得注意的是，工程测试时锤击点和测试点都位于钢轨轨顶。

本文采用该方法对轨道衰减率进行评价，并且将与激励点相隔一个单元长度(50 mm)的点作为0点，这也更符合工程测试实际。三种模型的轨道衰减率如图7所示。

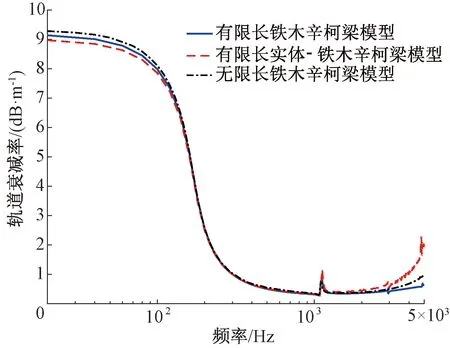
图7 三种模型的轨道衰减率

三种模型计算的轨道衰减率在低于3 000 Hz的范围内基本一致，低频段的轨道衰减率接近9 dB/m，该范围内的振动会沿轨道迅速耗散，在pinned-pinned频率附近出现峰值。

在高于3 000 Hz的频域范围，三种模型的轨道衰减率都有升高的趋势，但实体-铁木辛柯梁模型的上升幅度远大于另外两种梁模型。原因是在高频振动下，实体-铁木辛柯梁模型的激励原点截面会发生变形，且某些频率下变形后截面不再符合平截面假定，而梁模型的截面为刚性，所以实体-铁木辛柯梁模型钢轨在高频范围的动态阻尼较铁木辛柯梁模型偏大。

通常情况下，轨道衰减率往往通过静止谐载荷激励得到，而在实际中，钢轨受到的是移动轮轨力激励，移动谐载荷激励下的钢轨振动，可以通过文献[7]中式(42)计算移动谐载荷下的位移导纳得到移动谐载荷下的轨道衰减率，如图8所示。从图8可以看出，载荷前和载荷后的轨道衰减率有较大区别，前者整体大于后者，同时前者大于静止谐载荷轨道衰减率，后者小于静止谐载荷轨道衰减率。静止谐载荷会在pinned-pinned频率处(1 080 Hz)出现峰值，而在移动谐载荷作用时pinned-pinned频率会出现分叉(载荷前变为1 020、1 160 Hz，载荷后变为1 000、1 180 Hz)。

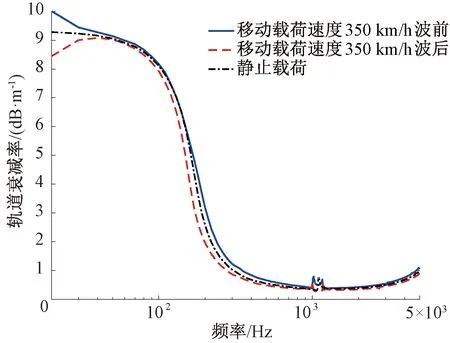
图8 移动谐载荷与静止谐载荷的轨道衰减率

4 钢轨辐射声功率分析

4.1 实体-铁木辛柯梁钢轨和无限长铁木辛柯梁声辐射对比

图7表明实体-铁木辛柯梁钢轨和铁木辛柯梁钢轨在高频段的轨道衰减率有较大差异，根据式(2)易知轨道衰减率对钢轨的辐射声功率具有较大影响。基于式(2)，可以得到单位垂向谐载荷作用下的实体-铁木辛柯梁钢轨和无限长铁木辛柯梁钢轨辐射声功率，如图9所示。载荷作用于相邻扣件之间的跨中位置，载荷频率范围为10～5 000 Hz，步长为10 Hz。对于实体-梁组合模型，载荷施加在跨中截面的中心轴处。

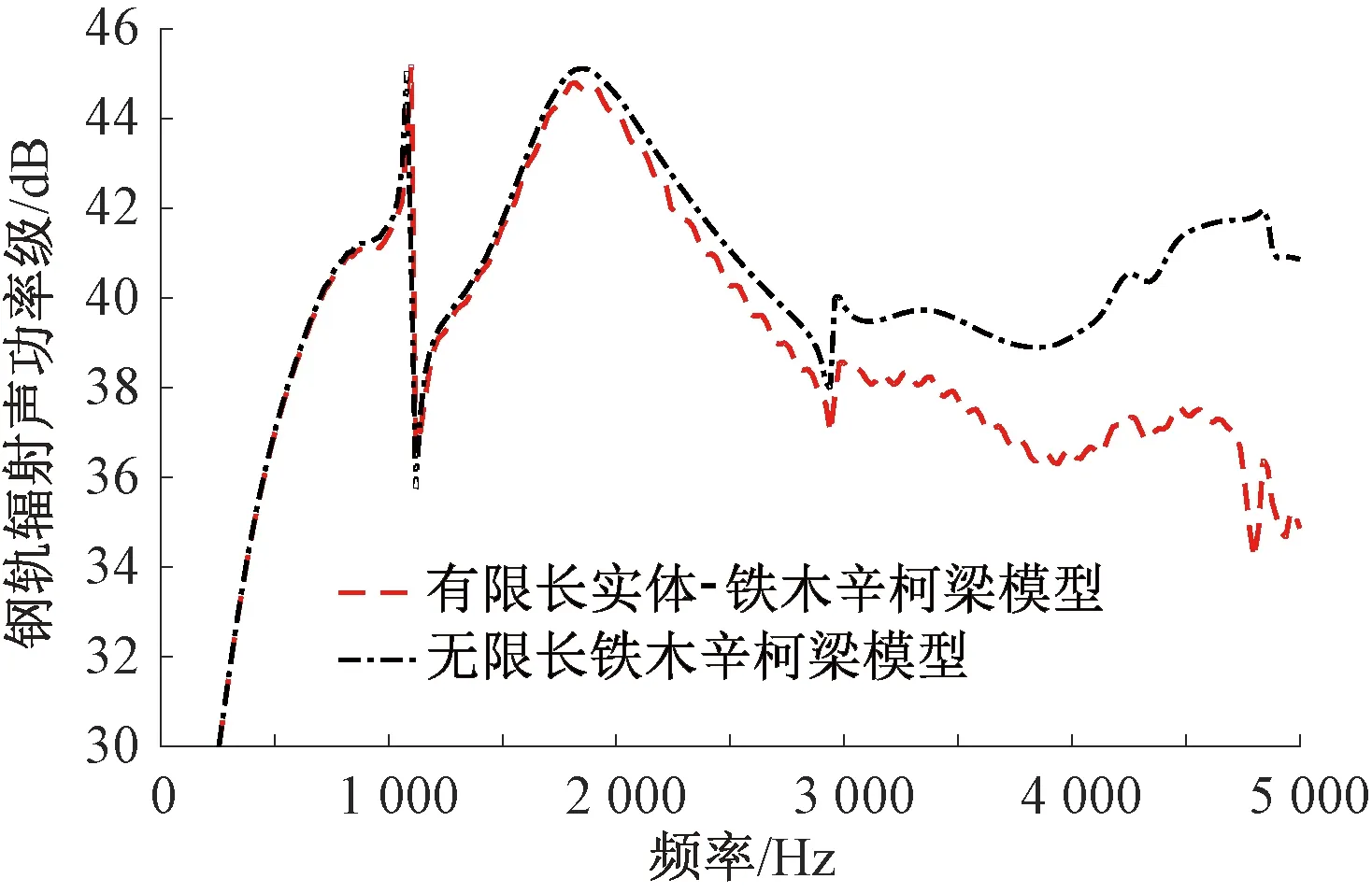
图9 有限长实体-铁木辛柯梁组合模型和无限长铁木辛柯梁模型的辐射声功率对比

从图9可以看出，有限长实体-铁木辛柯梁组合模型的辐射声功率在高于3 000 Hz时明显小于无限长铁木辛柯梁模型所计算的辐射，随着频率的增加，这种差异也随之增大，在5 000 Hz时差异可以达到6 dB。由式(2)可知，当轨道衰减率增加时，辐射声功率会减小，原点速度导纳增加时，辐射声功率会增大。由图6和图7可知，频率高于3 000 Hz时，实体-铁木辛柯梁模型的原点速度导纳大同时轨道衰减率也大，但轨道衰减率的差异更大，所以实体-铁木辛柯梁模型的声功率级更小。

4.2 式(2)与式(3)的声辐射对比

根据式(2)和式(3)得到的自由场钢轨辐射声功率级如图10所示。

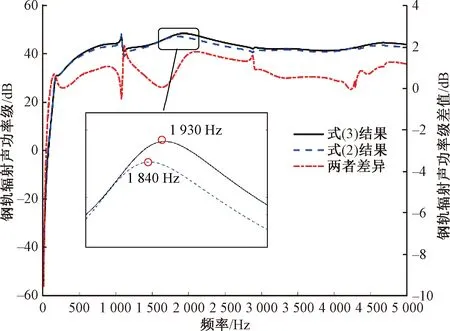
图10 钢轨辐射声功率级对比

由图10可以看出：

(1)频率低于150 Hz时，式(3)得到的钢轨声功率小于式(2)的声功率，这是由于在该频段，钢轨的衰减率较大，钢轨趋近于偶极子声源，与式(2)线声源的假设不符。

(2)高于150 Hz的大部分频率，式(3)得到的钢轨声功率大于式(2)的声功率，最大高约2 dB，这是由于式(2)的推导是在连续弹性支撑梁的基础上进行的，而在扣件等效刚度相等时，连续弹性支撑梁的声辐射会低于离散支撑梁。差异的峰值出现在第一、第二阶pinned-pinned频率及2 000 Hz附近。将该区域放大可以发现，两种方法得到的辐射声功率频率峰值存在差异，式(2)的峰值在1 840 Hz，式(3)的峰值出现在1 930 Hz，差异出现的原因在于式(2)的方法忽略了声在轨道方向传播的波动性，该波动性对声辐射的影响将在4.3节中进行详细阐述。

(3)两个公式均预测了pinned-pinned频率附近的峰值。

4.3 刚性轨道板对钢轨辐射声功率的影响

在实际情况中，钢轨作为声源并不存在于自由声场中。对于高速铁路无砟轨道而言，钢轨位于轨道板上方，因此有必要考虑钢轨位于轨道板上方时的辐射声功率，由于轨道板表面阻抗很大，可以认为声波在轨道板表面发生了全反射，通常可以构造镜像声源来模拟刚性反射面，如图11所示。用式(3)可以得到考虑轨道板反射时的钢轨辐射声功率，其中的声压是考虑了源钢轨与镜像钢轨的相互影响后得到的声压。

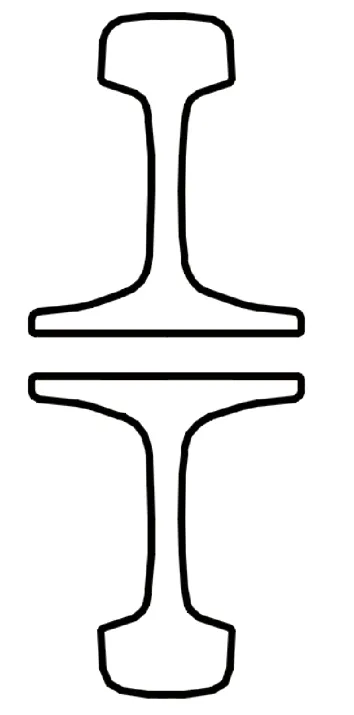
图11 钢轨及钢轨镜像

目前的板式无砟轨道中，钢轨和轨道的间距常常处于40～100 mm之间，所以本文计算了间距分别为40、60、80 mm三种工况的钢轨辐射声功率，如图12所示。

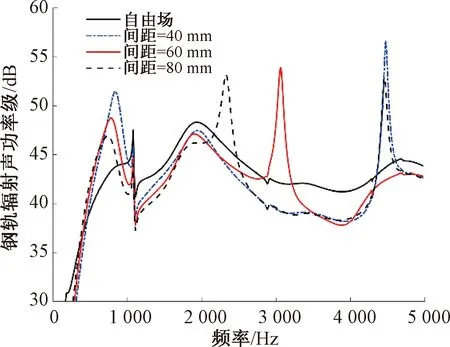
图12 刚性轨道板上钢轨的辐射声功率

从图12可以看出：相比于自由场下的钢轨辐射声功率，考虑轨道板的反射后最显著的特征是会出现一些峰值，对应于40、60、80 mm三种工况，峰值分别出现在830、4 470 Hz，790、3 060 Hz，730、2 320 Hz。随着距离的增加，峰值频率会减小，峰值的幅值也会降低。

为了探明这些峰值产生的原因，分别画出不同激振频率和不同轨道方向波数时单位力激励的钢轨振动速度谱，如图13所示，图13中的色彩代表力作用点处钢轨的振动速度水平，粗黑线是自由钢轨的频散曲线，以及以单位速度振动时钢轨表面平均声压谱(即钢轨同一截面上，表面各点声压的平均值，钢轨不同截面振动速度相同因此声压分布也相同)，自由空间和刚性轨道板上方钢轨的表面平均声压如图14和图15所示。图13～图15中颜色越深红表示振动速度/声压的幅值越大。

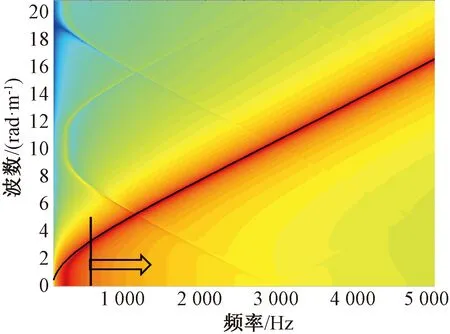
图13 无限长周期离散支撑钢轨的速度谱

图14 自由空间钢轨的表面平均声压

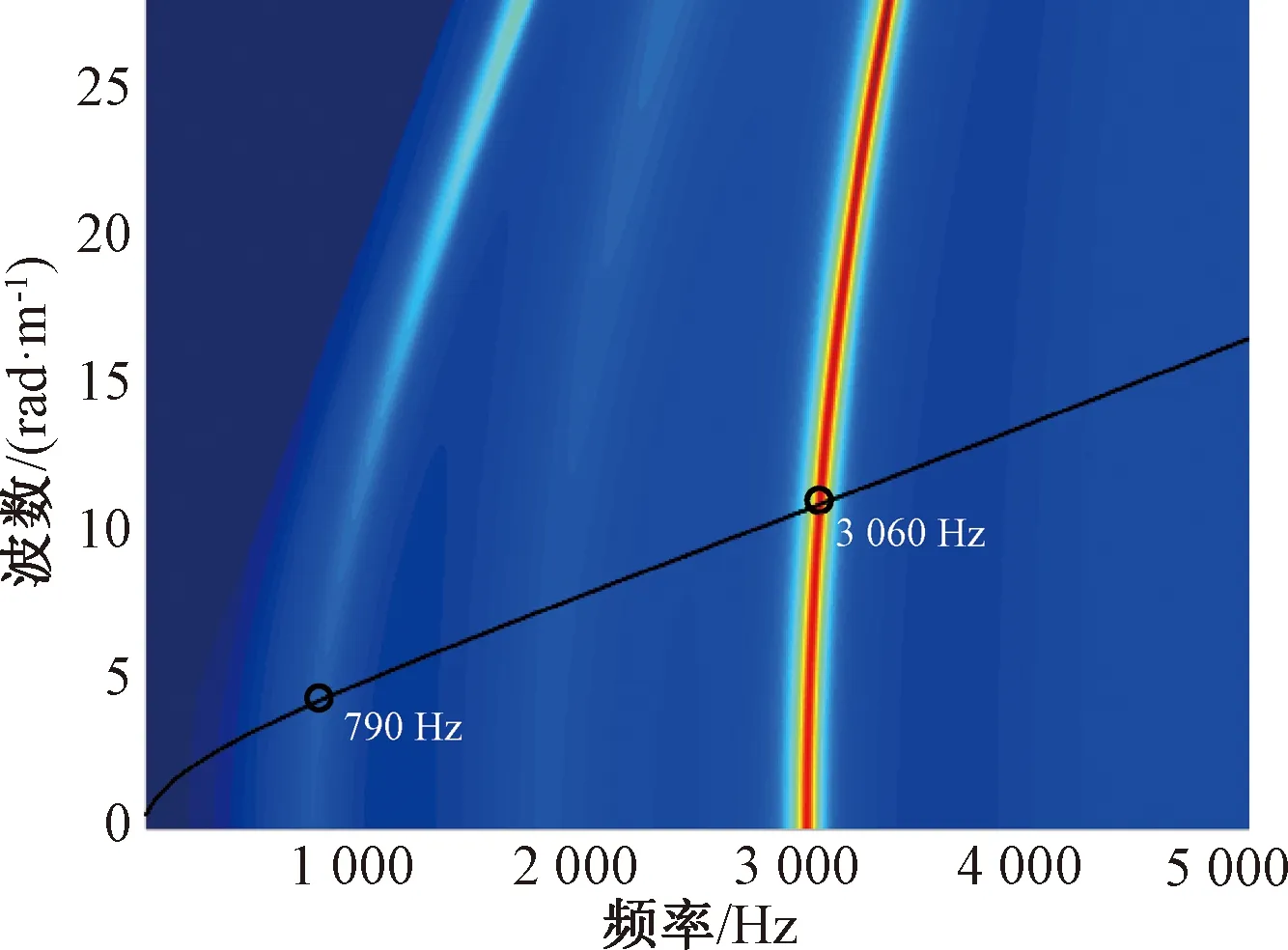
图15 刚性轨道板上方钢轨(间距为60 mm)的表面平均声压

由图13可以看出，钢轨的振动能量主要由弯曲波提供，但由于离散支撑的存在，频率在500 Hz以下的弯曲波与自由钢轨存在一定差异。易知随着扣件刚度的增加，该频率也会随之增加，170 Hz是一个cut-on频率。

对于声压谱，由图14可以看到，自由场中的钢轨声压在2 000 Hz附近存在一条亮带，这条亮带是由钢轨本身的声学边界形状所决定的，波数为0时，亮带的中间频率为1 840 Hz，这一频率正是式(2)计算得到的一个钢轨声功率峰值，但式(3)得到的声功率峰值出现在这条亮带与钢轨弯曲波频率曲线的交点上，这一交点的对应频率为1 930 Hz；由图15可以看到，具有反射面声场中的钢轨声压相比于自由场钢轨声压新增了两条亮带，这两条亮带由钢轨和轨道板的间距所决定，可以看到两条亮带与钢轨频散曲线的交点(790、3 060 Hz)正是图12中的钢轨辐射噪声峰值频率。值得注意的是，钢轨的声压由式(5)决定。钢轨的声压谱为何会产生峰值，笔者认为可能由特征波导致，但钢轨振动速度为0时，其声压谱的峰值在图14和图15中并不相同。对此笔者还在进一步研究。

5 结论

(1) 使用有限长钢轨模型计算振动特性，端部导纳和原点导纳比值最大不超过20%时，其原点导纳与无限长钢轨模型基本一致，不会出现因截断边界产生的波动，此时可以将有限长钢轨近似为无限长。

(2) 使用MPC连接实体模型和铁木辛柯梁钢轨模拟钢轨，在保留实体钢轨模型的优点同时，可以大量减少计算消耗。当网格划分合适，实体-梁钢轨模型的动力响应结果在高于3 000 Hz的频率比梁单元钢轨的可信度更高。无限长铁木辛柯梁模型相比另外两种模型计算更为方便，可以集成轨道模型和声学边界元模型建立轨道系统噪声预测软件。

(3) 由于实体-梁钢轨模型在高频会产生较多的变形，所以导纳和轨道衰减率会比梁钢轨模型更大，这也会导致实体-铁木辛柯梁组合模型在高频段的辐射声功率比铁木辛柯梁模型小了很多，而且这个差异随着频率的增加而增大。

(4) 由于多普勒效应，移动谐载荷下的轨道衰减率在pinned-pinned频率处会出现两个峰值，同时荷载前的钢轨衰减率要大于荷载后的钢轨衰减率。

(5) 相比于基于周期离散支撑钢轨振动和2.5维边界元计算钢轨声功率的方法，基于轨道衰减率和2维边界元法的钢轨声功率传统方法的结果在150 Hz以下高估了钢轨声功率，在150 Hz以上低估了钢轨声功率。

(6) 刚性轨道板会使钢轨辐射声功率出现多个峰值，峰值频率随钢轨与轨道距离的增加而减小，其原因是峰值频率位于钢轨的速度谱与声压谱亮带的交点上，声压谱亮带频率随距离的增加而降低。

鸣谢

在本文的研究过程中，多次与英国南安普敦大学声与振动研究所(ISVR)的D.J.Thompson教授进行了讨论，得到了他的大力指导。