基于CFD-DEM的有砟道床多孔介质模型研究

殷 浩，高 亮

(1.北京交通大学 土木建筑工程学院， 北京 100044；2.北京交通大学 轨道工程北京市重点实验室， 北京 100044)

有砟道床由散粒体的道砟颗粒堆积密实而成，随着行车速度的提高，会出现道砟颗粒飞离道床，击打车辆、轨道及线路周边设施的情况，即道砟飞溅现象。近年来，高速铁路道砟飞溅现象持续增多[1-4]，其对轨道结构和列车具有巨大危害，极大增加了线路和车辆的养护维修成本，威胁行车安全。

道砟飞溅受轨道结构流场特征影响显著，为分析其发生和发展机理，国内外学者开展了大量研究工作。基于数值方法的有砟轨道流场特征分析，在飞砟机理研究中起到了不可或缺的作用，通过计算还原轨道流场，能够准确分析道砟飞溅易发生区域及其发展规律。Sima等[5]较早采用计算流体动力学(CFD)方法建立了车厢底部与轨道结构的数值模型，对基于轨道流场特征的道砟飞溅机理进行仿真研究。Rocchi等[6]采用高速铁路线路测试数据对所建立的有砟轨道CFD数值模型进行验证，并分析了轨道流场与道砟所受荷载之间的关系。殷浩等[7]建立了轨道与车厢结构的数值模型，并精确考虑二者外形因素影响，分析了行车速度和道床尺寸等参数对道砟飞溅的影响。

有砟道床的散粒体特征对轨道流场影响显著，但既有仿真研究多采用连续壁面单元(wall单元)对散体道床进行模拟，无法反映道砟级配和形状等颗粒特征对轨道流场的影响，不能准确分析道砟飞溅的发生和发展机理。García等[8-9]通过设置道床壁面单元的等效粗糙度参数，模拟道床表面的不连续特征。然而，该方法仍是对道床表面颗粒特征的过度简化，且无法反映散体道床对流经其内部流体的影响。

郄录朝等[10]在开展道砟飞溅CFD仿真分析时，将有砟道床考虑为多孔介质模型，通过现场试验数据对模型参数进行标定。多孔介质模型能够反映结构内部的孔隙特征，真实还原散粒体道砟对流经道床流体的阻力影响，该方法有效提高了流场的还原精度。然而，道床多孔介质模型参数在不同线路条件下的差异显著，采用现场试验的参数获取方法成本较高，且无法得到既有线路之外的道床模型参数。

针对上述问题，本文提出有砟道床的计算流体动力学-离散元(CFD-DEM)耦合分析方法，采用基于CFD-DEM耦合的精细计算方法，对局部道床多孔介质模型中所涉及的关键参数进行获取和验证。该参数获取方法既能反映道砟级配和形状等颗粒特征，还能体现道床与流体的相互作用，实现了轨道流场的真实还原。为精确分析基于大尺度的有砟轨道流场特征的飞砟发生机理，以及基于道砟飞溅运动特征的飞砟发展机理提供了必要的技术手段。

1 有砟道床CFD-DEM耦合分析方法

采用DEM分析模块对有砟道床进行模拟，能够反映道砟形状、级配、位置等颗粒特征；采用CFD分析模块计算流经道床的轨道流场，能够反映散体道床与流体的相互作用关系。通过编制CFD-DEM耦合算法自定义函数，描述有砟道床与流体之间的动量和质量数据传递，真实还原有砟轨道流场特征，对道床多孔介质模型参数进行获取和验证。

1.1 有砟道床DEM分析模块

采用DEM模拟有砟道床结构，将道砟颗粒考虑为相互独立的单元个体。采用Hertz-Mindlin接触模型计算颗粒之间接触力，根据牛顿第二定律建立运动方程，计算颗粒在迭代时步内的位移，进而对道砟颗粒的位置信息进行更新。道砟颗粒单元的运动方程为

(1)

式中：m为颗粒质量；u为颗粒位移；Fi为道砟颗粒与流体之间的相互作用力；F为颗粒间作用力。

不同形态特征的道砟颗粒在流场中的受力和运动特征差异显著，本文采用三维激光扫描法，对道砟颗粒的真实外形进行获取[11-12]，并将其作为模板导入DEM计算模块。该道砟轮廓模板仅以虚拟面的形式存在，无法考虑道砟颗粒之间的相互作用，故采用单元球模型对其进行填充。根据道砟轮廓模板的形状和尺寸，确定填充球单元的位置和粒径。不同形状特征的道砟轮廓模板，以及填充后的道砟单元模型见图1。

图1 道砟颗粒DEM模型示意图

在计算空间内随机生成不同形态状特征的道砟颗粒仿真单元，构成有砟道床离散元数值模型。根据TB 10621—2014《高速铁路设计规范》[13]，设置道床顶面宽度3.6 m，道床厚度0.35 m，边坡坡度1∶1.75。模型中的结构单元体均满足刚性假设，参考文献[14-15]开展的有砟道床离散元仿真分析，并结合课题组既有研究，确定道砟模型细观参数见表1。

表1 道砟DEM模型参数

在道床模型建立过程中，需分层生成道砟颗粒，并采用墙体单元以较慢的速度对其逐层压实，确保每层道砟均达密实稳定状态。建立的有砟道床DEM分析模块见图2。

图2 有砟道床DEM分析模块

1.2 轨道流场CFD分析模块

流体的流动需满足质量守恒定律，即单位时间流体微元体增大的质量，与流入微元体的净质量相等。在此基础上，通过在守恒方程加入额外的颗粒单元体积分数项ε，考虑道砟颗粒对流体的影响，流体质量守恒方程为

(2)

式中：u、v和w是速度矢量分别在x、y和z方向上的分量；ρ为流体密度；t为时间。

流体流动还需满足动量守恒定律，即微元体中流体动量对时间的变化率与微元体所受合外力相等，动量守恒方程也需考虑颗粒单元体积分数项ε的影响，表达式为

(3)

(4)

(5)

式中：μ为流体动力黏度；P为流体微元体压力；Su、Sv和Sw为动量守恒方程广义源项。

采用多面体单元对轨道流场CFD分析模块的计算域进行网格划分，该模块中的轨道结构尺寸与DEM模块一致，所建立的网格模型见图3。在CFD-DEM耦合算法中，CFD模块与DEM模块中数据的交互传递是以全局坐标为基础开展的，故需确保二者具有相同的全局坐标，进而实现道砟颗粒与其所处区域轨道流场的相互关联。

图3 轨道流场CFD分析模块

1.3 CFD-DEM耦合算法

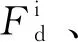
(6)

式中：ρf为流体密度；Ap为颗粒投影面积；Vf和Vp分别为流体和颗粒的体积；Cd、κ分别为阻力系数及幂指系数，计算式分别为

(7)

(8)

其中，Re为雷诺数。

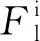
(9)

(10)

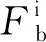
(11)

式中：Cb为附加体力系数，取0.5。

DEM模块与CFD模块通过网格单元进行数据交换，颗粒单元体积分数项ε的获取也在网格单位开展。计算耦合模块的颗粒体积分数项时，首先对颗粒单元的质心坐标进行检索，若颗粒质心位于目标网格单元区域内，则认为该颗粒属于目标网格单元，颗粒体积也被计入目标网格单元的体积分数项的计算中[18]。网格单元颗粒体积分数项ε可计算为

(12)

式中：Vmesh为网格单元体积；Vi为质心位于所计算流体网格单元内部的颗粒单元体积；n为该网格单元中颗粒数量。

在每个计算时步内，CFD模块首先检索计算域内流场的初始参数，以及颗粒单元的位置信息。在此基础上，对流场数据进行求解计算，收敛后进一步计算流场对处于其内部的每枚颗粒单元受到的作用力Fi。DEM模块通过颗粒运动状态以及颗粒与其他颗粒单元或边界单元之间的接触状态，计算DEM模块中颗粒所受到的接触力。并进一步考虑CFD模块对颗粒产生的作用力，由牛顿运动定律，计算颗粒的位置和速度等运动信息。在下一个时步内，将DEM模块中更新颗粒运动信息后的颗粒模型数据导入CFD计算模块中，再次重新检索计算域内流场参数和颗粒位置信息，对流场数据和颗粒受力进行求解，依次开展迭代计算，直至满足计算条件要求。在计算域边界位置，采用面网格单元对DEM中的计算边界进行描述，进而实现与CFD网格边界单元的耦合对应。

基于CFD-DEM耦合分析方法的有砟轨道模型计算精度，由DEM模块计算精度、CFD模块计算精度，以及二者之间的耦合算法共同控制。其中，DEM模块计算精度会受到分析时间步长、接触模型、道砟颗粒球簇单元填充数量和质量等因素的影响；CFD模块计算精度会受到分析时间步长、网格类型和尺寸、控制模型等因素的影响；CFD-DEM耦合算法主要通过控制两个模块之间的数据交换频率影响分析计算精度。CFD-DEM耦合算法流程见图4。

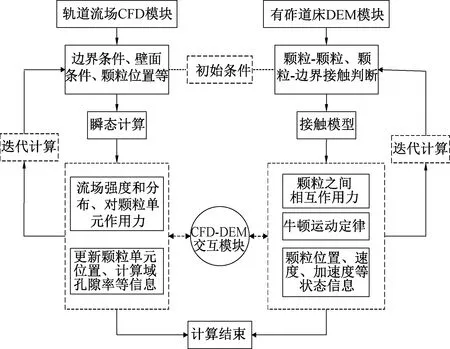
图4 CFD-DEM耦合算法流程

2 有砟道床多孔介质模型

在采用CFD-DEM耦合算法开展轨道流场分析时，在每个迭代时步内均需对大量道砟颗粒单元的位置和受力信息进行遍历检索。若采用该方法开展局部范围的轨道流场分析，其计算精度和效率均较高；而在涉及大尺度的高速列车-有砟轨道的流场分析时，计算效率会受到DEM模块算法的限制而显著不足。故本文将有砟道床考虑为能反映道床对流体阻力影响的多孔介质模型，采用CFD-DEM耦合算法对道床多孔介质模型参数进行获取和验证。为研究基于大尺度高速列车-有砟轨道道砟飞溅流场特征和运动特征的飞砟机理提供技术手段。

2.1 多孔介质数学模型

有砟道床是由道砟颗粒和空气组成的多相物质；道砟颗粒间的孔隙相对较小，道砟占据道床结构的绝大部分区域；颗粒间孔隙能够相互连通，使空气能够在其内部和表面流动。有砟道床的上述结构特征符合Bear[19]、Warrick等[20]对多孔介质结构的定义，故在分析道床流场特征时，可将其考虑为多孔介质结构。

有砟道床多孔介质模型能够反映道床对空气流场的阻力作用，在数学模型上表现为流体动量方程的附加动量源项Si，该附加动量源项由黏性损失项和惯性损失项两部分构成，各向同性多孔介质的动量源项Si可表示为

(13)

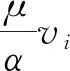
附加动量源项Si与流经多孔介质模型的压力梯度直接相关，故结合式(13)可知，道床上下游的流体压降与流经道床的流体速度之间的关系为

(14)

式中：Δn为沿流体流动方向的道床纵向长度。

2.2 基于CFD-DEM的多孔介质参数获取

基于有砟道床 CFD-DEM 耦合算法，计算提取流经道床的流体压降，并将其与流场风速拟合，得到压降与风速拟合关系式，将该关系式与多孔介质模型的动量方程附加源项对比分析，得到道床模型的黏性阻力系数和惯性阻力系数，实现道床多孔介质模型参数的获取。

将沿道床模型纵向的边界条件分别设置为风速入口边界和压力出口边界，其他表面均为无滑移壁面条件，用于限制道床内道砟颗粒单元的流出，见图5。当流场达稳定后，分别对道床入口和出口边界面处的风压数据进行积分，提取流场上游和下游平均风压，计算得到流经道床的空气流场压降。当入口边界的输入风速为10 m/s时，计算过程中的流场压降曲线见图6。由图6可知流场压降先逐渐增大，后趋于稳定，提取该稳定值作为耦合模型的压降数据。

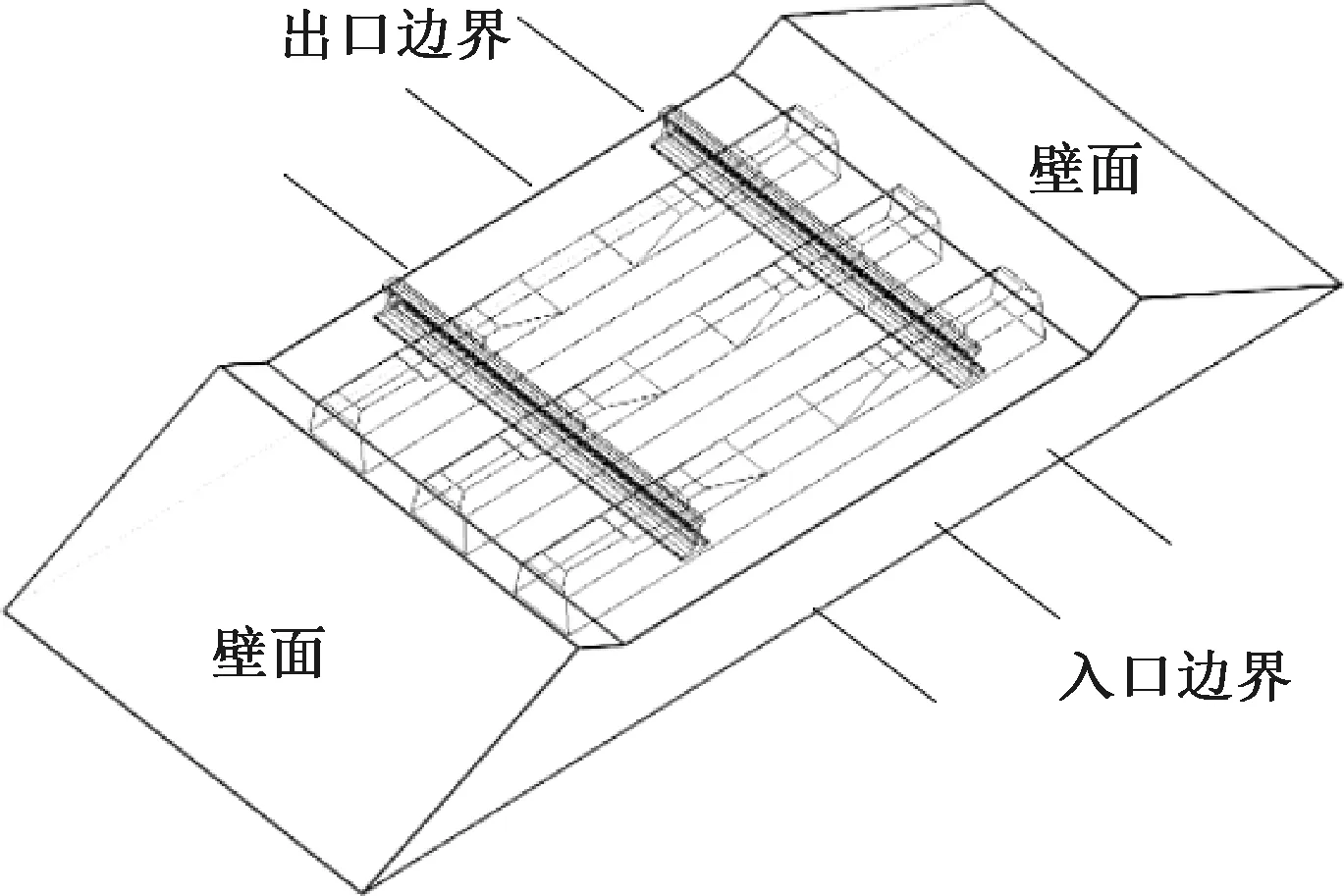
图5 耦合模型边界条件

图6 流体压降曲线(流速10 m/s)

设置入口风速分别为 5、10、15、20、25、30 m/s，计算模型上下游流场压降，提取不同输入风速条件下的压降数据。将输入风速与压降数据进行二次拟合，拟合曲线见图7，压降ΔP与风速v之间的拟合关系式为

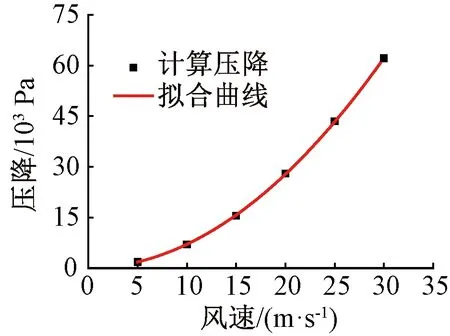
图7 流体压降与输入风速关系

ΔP=68.307v2+24.735v

(15)

拟合曲线相关系数R2=0.999 7，可认为二者完全相关。

将式(15)与式(14)比对分析，可得到道床多孔介质模型的黏性阻力系数与惯性阻力系数。Δn取沿流体流动方向的道床纵向长度1.8 m，考虑外界条件为标准大气压强101.325 kPa，温度20 ℃，此时空气密度ρ=1.205 kg/m3，空气黏度μ=1.79×10-5Pa·s。通过计算，得到道床多孔介质模型的黏性阻力系数1/α=767 678，惯性阻力系数C′=62.984 9。

2.3 多孔介质模型参数验证

将由CFD-DEM耦合算法计算得到的黏性阻力系数1/α与惯性阻力系数C′施加于有砟道床多孔介质CFD模型中，将其设置为与耦合算法相同的边界条件，开展流场仿真计算。将采用道床多孔介质CFD模型与CFD-DEM耦合模型计算得到的有砟轨道风压分布和压降数据对比分析，对该参数获取方法进行验证。

将CFD-DEM耦合模型与道床多孔介质模型的计算域入口风速均设置为10 m/s。耦合模型中流体流经道床时的道砟颗粒压强云图见图8。由图8可知，颗粒模型统一显示为圆球单元，未体现其外形和粒径特征。

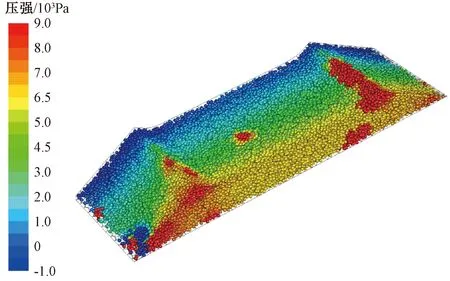
图8 CFD-DEM耦合模型道砟颗粒压强云图

由图8可知，不同区域道砟受到的压强差异显著。流场入口附近颗粒多受正压影响，出口附近颗粒多受负压影响，且正压幅值显著高于负压幅值。道床上游与下游之间道砟所受压强均匀变化，该压强变化即为流体流经道床产生的压降，是由散体道床对空气流体的黏性阻力和惯性阻力作用所致。同时，道床内部也存在所受压强异常变化的道砟，主要分布在砟肩和边坡坡底等区域，这是因为该区域道床密实程度较道床内部其他区域更低，流场作用下颗粒会产生不同幅度的错动；同时，道砟颗粒的形状、尺寸和所处状态各不相同，其受到流场作用的影响也存在差异，导致局部区域道砟所受风压的异常变化。

道床多孔介质CFD模型计算得到的线路中心横、纵断面风压云图见图9。由图9可知，由于将散体道床考虑为多孔介质结构，导致道床横向流场的分布较为均匀，无大幅度的波动情况。在沿线路纵向上，流场的分布和强度特征与CFD-DEM耦合模型的计算结果较为一致，均存在均匀过度的风压梯度，且在计算域入口附近风压为正，出口附近为负，在该风压梯度作用下产生流场压降。当输入风速为10 m/s时，道床多孔介质模型的流场压降曲线见图10，由图10可知，该风速条件下，流体流经道床多孔介质模型前后的压降为7 218 Pa，与采用CFD-DEM耦合模型得到的流场压降仅相差2.82%。

图9 道床多孔介质模型截面风压云图

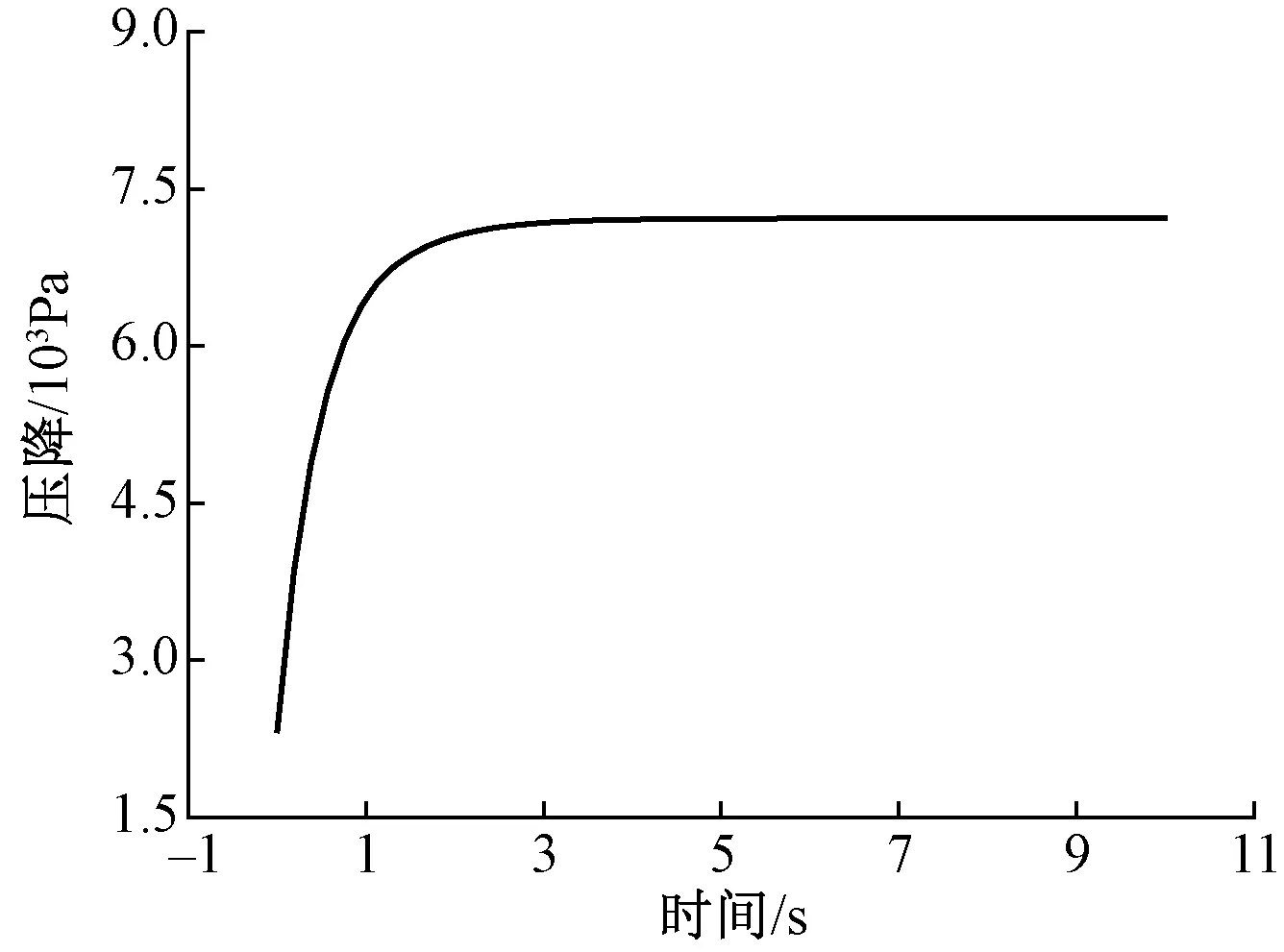
图10 多孔介质道床模型压降曲线

计算输入风速分别为5、10、15、20、25、30 m/s条件下的道床流场压降。在不同输入风速条件下，采用有砟道床CFD-DEM耦合模型，以及基于CFD仿真方法的道床多孔介质模型达计算收敛后，流经道床的流体压降对比情况见表2。

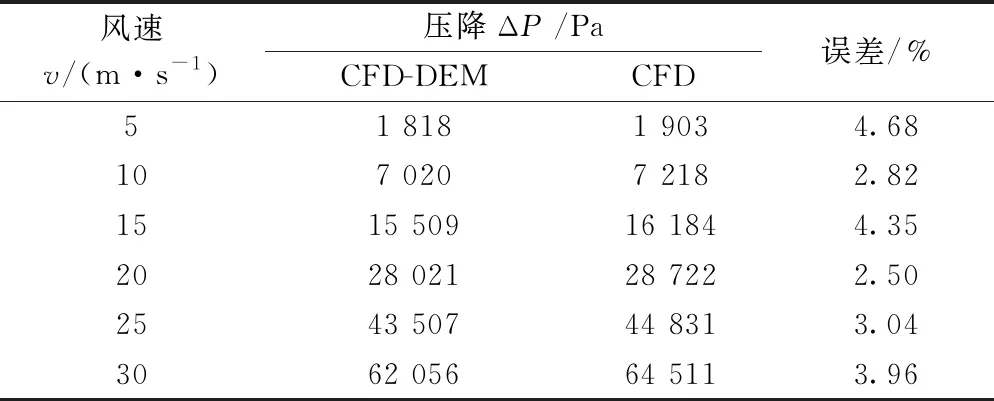
表2 道床耦合模型与多孔介质模型压降对比

由表2可知，基于道床多孔介质CFD模型计算得到的流场压降，较CFD-DEM耦合模型的计算数据非常相近，二者最大误差不超过5%，即可认为采用CFD-DEM耦合模型计算得到的道床参数，可应用在基于道床多孔介质模型的CFD仿真分析中。同时，采用道床多孔介质模型大幅提高了仿真计算效率，为基于大尺度高速列车-有砟轨道流场特征和运动特征的道砟飞溅机理研究，提供了重要的技术手段。

4 结论

本文将有砟道床考虑为能够反映其对流场黏性阻力和惯性阻力影响的多孔介质模型，基于提出的有砟道床CFD-DEM耦合分析方法，对道床多孔介质模型关键参数进行获取和验证。

(1)有砟轨道CFD-DEM耦合分析方法，既能反映道砟的级配、形状、位置等颗粒特征，又能体现道床与流体的相互作用关系，实现了有砟轨道结构的准确模拟。

(2)应用CFD-DEM参数获取方法建立的有砟道床多孔介质模型，能够准确模拟有砟道床对流体的黏性阻力和惯性阻力影响，模拟最大误差仅为4.68%，实现了有砟轨道流场特征的真实还原。

(3)基于CFD-DEM耦合的道床多孔介质模型参数获取及验证方法，为研究大尺度高速列车-有砟轨道的道砟飞溅流场特征和运动特征提供了技术手段。