关于函数零点的存在性证明的讨论
◎刘顺琴(厦门大学嘉庚学院,福建 漳州 363105)
高等数学是高等学府里理工科学生的必修科目之一,在理工类学生的专升本考试或者研究生入学考试当中,也是必考科目之一.由此可见,高等数学十分重要.
高等数学以函数为核心,系统地介绍了函数的极限、导数、导数的应用、不定积分、定积分、微分方程、空间解析几何及多元函数的微积分等内容.高等数学作为一门研究函数的学科,有很多经典的问题.本文主要从应用零点定理展开的证明、应用微分中值定理展开的证明、利用单调性证明根的个数三方面进行总结和讨论.
一、应用零点定理展开的证明
闭区间上的连续函数具有很多的特殊性质,比如最值定理、介值定理、有界性定理,还有零点定理(根的存在性定理),其中零点定理就可以用来证明函数在给定区间上有零点.
零点定理:设函数f(x)在闭区间[a,b]上连续,且f(a)f(b)<0,
则在开区间(a,b)内,至少存在一个ξ∈(a,b),使得f(ξ)=0.
该定理的条件和结论都比较简单,在几何上也是非常直观的,所以利用该定理来证明,思路简单、直接.
利用零点定理证明零点的存在性的步骤:
第一步:构造闭区间上的连续函数;
第二步:验证闭区间上的连续性和端点函数值的异号性;
第三步:得出结论.
例1证明方程x=asinx+b(a>0,b>0)至少有一个正根,并且它不超过a+b.
证明:该题相当于证明函数f(x)=x-asinx-b在开区间(0,a+b]内至少有一个零点.所以证明如下:
令f(x)=x-asinx-b,则根据初等函数在有定义的区间内都连续,可以得出f(x)=x-asinx-b在闭区间[0,a+b]上连续,且
f(0)=0-asin 0-b=-b<0,f(a+b)=(a+b)-asin(a+b)-b=a[1-sin(a+b)].
由于sin(a+b)≤1,所以下面分两种情况讨论:
情况一:sin(a+b)=1.
若sin(a+b)=1,则f(a+b)=(a+b)-asin(a+b)-b=a[1-sin(a+b)]=0,则x=a+b为方程所要求的不超过a+b的正根;
情况二:sin(a+b)<1.
若sin(a+b)<1,则f(a+b)=(a+b)-asin(a+b)-b=a[1-sin(a+b)]>0,此时
f(0)f(a+b)<0,根据零点定理,在开区间(0,a+b)内,存在一个f(x)=x-asinx-b的零点,即x=asinx+b在开区间(0,a+b)内有一根.
综上,该题得证.
证明该题的时候,要注意分类讨论,零点定理只是其中的一种情况.
二、应用微分中值定理展开的证明
在函数的导数部分,有三个非常重要的微分中值定理:罗尔定理、拉格朗日中值定理、柯西定理.这三个定理都可以用来证明函数的导函数在给定区间内有根,其中以罗尔定理的应用最为典型.
罗尔定理:设函数f(x)满足:
(1)f(x)在闭区间[a,b]上连续,
(2)f(x)在开区间(a,b)内可导,
(3)f(a)=f(b),
则在开区间(a,b)内至少存在一个ξ,使得f′(ξ)=0.
该定理区别于零点定理,首先条件要求更高,结论也发生了比较大的变化,是由原函数的性质推导出来的导函数的零点的存在性.该定理在直观上可以描述为连续可导的函数的两个等高点之间至少有一个导函数的零点.
例2设f(x)=x(x-1)(x-2)…(x-100),不求导数,判断f(x)的导函数有几个零点.
解:根据初等函数的连续性和可导性可知,函数
f(x)=x(x-1)(x-2)…(x-100)在(-∞,+∞)上任意点连续且可导,且易知
f(0)=f(1)=f(2)=…=f(100)=0,则在(0,1)内,至少存在ξ1,使得f′(ξ1)=0;同理在(1,2)内、在(2,3)内、…、在(99,100)内,均各有一个使f′(x)=0的x,注意到这些区间互不交叉,所以f′(x)至少有100个零点;
又由于f(x)是101次多项式,所以f′(x)是100次多项式,根据多项式的零点理论可知,f′(x)至多有100个零点.
综合上面两种情况可知,f′(x)恰好有100个零点.
事实上,根据上面的讨论过程,我们还可以知道f″(x)恰好有99个零点,f‴(x)恰好有98个零点,f(n)(x)(1≤n≤100)恰好有(101-n)个零点.
该题的题意清晰,证明难度较低,我们接着来看例3.
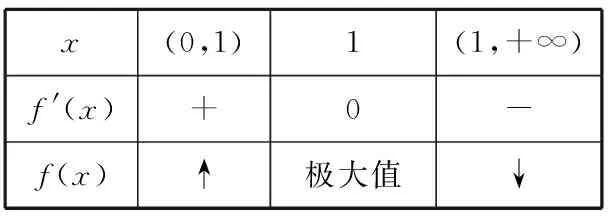
例3设f(x)在[0,a]上连续,在(a,b)内可导,f(a)=0,0 思路:该题相当于证明2f(x)+xf′(x)在(a,b)内有零点,显然直接使用零点定理条件不足,考虑使用罗尔定理,此时2f(x)+xf′(x)的原函数在直观上求不出来.这种情况一般可以描述为: 这就转化成了证明函数 下面用该思路来证明例3. 有时候,证明函数在区间[a,b]内有零点,可以转化为证明函数在包含在[a,b]的小区间内有根.比如下方的例4. 例4已知函数f(x)在区间[0,1]内二阶可导,且f(0)=f(1).证明:存在ξ∈[0,1],使得(1-ξ)f″(ξ)=3f′(ξ). 证明:由题设f(0)=f(1)和f(x)在区间[0,1]内二阶可导易知,f(x)在区间[0,1]上满足罗尔定理,所以存在a∈(0,1),使得f′(a)=0. 另外由结论(1-ξ)f″(ξ)=3f′(ξ),我们希望构造函数(1-x)f″(x)-3f′(x)的原函数,这在直观上是不好求的,令u(x)=(1-x)2,则u(x)[(1-x)f″(x)-3f′(x)]=(1-x)3f″(x)-3(1-x)2f′(x)的原函数是好构造的,令F(x)=(1-x)3f′(x),则F(a)=F(1)=0,且易知F(x)在区间[a,1]上满足罗尔定理的条件,则存在ξ∈[a,1],使得F′(ξ)=(1-ξ)3f″(ξ)-3(1-ξ)2f′(ξ)=0,即(1-ξ)3f″(ξ)=3(1-ξ)2f′(ξ),又因为(1-ξ)2>0,所以(1-ξ)f″(ξ)=3f′(ξ),该例题得证. 关于函数的构造,经常考虑利用两个函数的零点. 例如f(a)=g(b)=0,则构造F(x)=f(x)g(x),F(x)满足F(a)=F(b)=0.例4已经充分说明了这一点:f′(x)满足f′(a)=0,g(x)=(1-x)3满足g(1)=0,所以构造了F(x)=f(x)g(x)=(1-x)3f′(x). 在学习了定积分之后,会出现证明含有定积分和导数的方程的根的存在性的问题. 从以上几个例子可以看出,利用中值定理证明函数在给定区间内有根的关键是构造出合适的函数,而函数也恰好是高等数学最基本的研究对象. 上面两种情况均只涉及函数在给定区间内零点的存在性.存在性告诉我们函数在给定区间内至少有一个零点,但是关于零点个数却没有办法解出.事实上,结合单调性和函数的极值,或者说结合函数的图像,关于函数的零点的存在性和个数可轻易解决. 首先给出关于单调性的定理: 定理:区间(a,b)内,f′(x)>0,则f(x)在(a,b)内单调递增; 区间(a,b)内,f′(x)<0,则f(x)在(a,b)内单调递减. 例6设函数f(x)=2lnx-x2+2. (1)求f(x)的单调性; (2)证明方程f(x)=0有两个不同的实根. (1)解:f(x)的定义域为(0,+∞), 令f′(x)=0,得x1=-1(舍去),x2=1. 列表如下: x(0,1)1(1,+∞)f '(x)+0-f(x)↑极大值↓ 如表所示,f(x)在(0,1]上单调递增,在[1,+∞)上单调递减. f(1)=2ln 1-1+2=1>0, f(e)=2ln e-e2+2=4-e2<0. f(ξ1)=0且f(ξ2)=0. 综上可得方程f(x)=0至少有两个不同的实根,结合单调性可知,f(x)=0恰好有两个不同的实根. 对于同类问题的研究思考及区分,能够在一定程度上提高学生的发散思维能力,增强学生的学习兴趣,提高学生的学习能力.学生在学期总结或知识点总结时进行必要的题型总结,能够强化自身综合思维能力,掌握解题技巧,并且轻松地举一反三.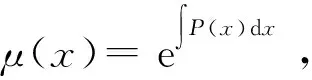
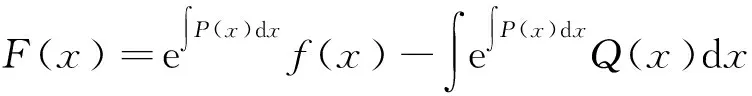
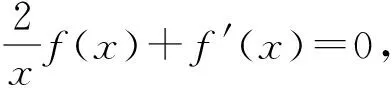

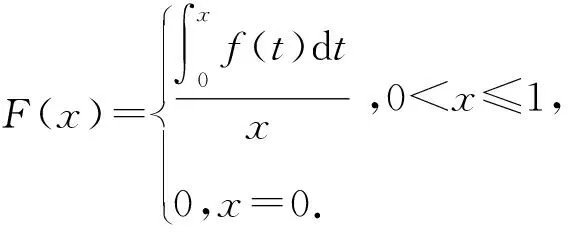
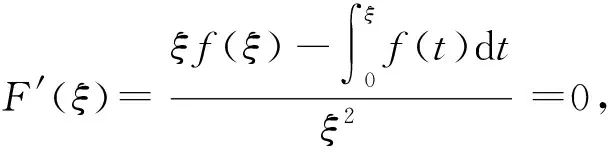
三、利用单调性证明根的个数

四、结 语

