考研背景下一般拓扑学中几个概念的讲授方法
◎庞 斌(北京理工大学数学与统计学院,北京 102488)
一、引 言
随着我国高校扩招,高校毕业生人数逐年增长,就业市场也日趋饱和.在这种大的教育背景下选择读研成为提高就业竞争力、完善自身知识结构以及实现自我价值的重要途径.因此,“考研热”给传统的本科生数学课程的教学模式带来新的冲击,有以下两方面的体现:
一方面,数学专业研究生入学考试考查内容数学分析、高等代数这两门课程在大二就已经学习结束.“考研热”导致很多学生过早地准备考研专业课的复习,所以对于后继专业课程的学习没有足够重视.这种学习模式的后果是学生只会熟练地解答数学分析和高等代数中的具体题目,但对于需要学习的其他高年级数学专业课程知之甚少.因此学生对本科阶段的数学课程没有整体的把握和理解,数学综合素质较差,许多考生在考研初试中取得较高成绩,但是因为综合能力差而在复试过程中被淘汰.
另一方面,“考研热”对于本科毕业论文指导过程产生影响.毕业论文要求学生将本专业所学知识和实践相结合,在深化所学知识的同时,突出知识的运用能力.这就要求学生具有扎实的基本功,除了熟练掌握基础课程,还要对各门高年级专业课程进行串联和梳理,整体把握整个数学课程体系的内容,从而提高对于所学知识的掌握能力以及创新运用能力.如果学生仅局限于考研课程的学习,会极大地限制学生的思维,导致毕业论文缺乏新意.
综上,在考研背景下,高年级的各类专业课程教学面临着新的挑战.教师不仅需要以学生能力的提升为目的调整教学内容,还要探索出既可以培养学生综合能力又能提高学生考研成功率的教学模式.本文主要针对一般拓扑学课程,结合该课程中的一些基本概念及其相关性质,探索合适的讲授方法和教学内容设计,帮助学生在学习一般拓扑学课程的同时,尽可能地去梳理数学分析课程脉络,尤其是对基础概念的深层次理解和掌握.论文呈现的讲授方法的实施有助于提高高年级学生的分析能力,同时有助于提高学生的知识整合能力以及创新能力,也会辅助提高数学专业学生的考研成功率.
二、基本概念
定义2.1 设X是集合.若τ⊆P(X)满足:
(T1)Φ,X∈τ;
(T2)∀A,B∈τ,A∩B∈τ;
(T3)∀{At}t∈T⊆τ,∪t∈TAt∈τ,
则称τ是X上的一个拓扑.相应地,序对(X,τ)称作一个拓扑空间.
定义2.2 设(X,τ)是一个拓扑空间,U⊆X,x∈X.若存在V∈τ使得x∈V⊆U,则称U是x的一个邻域.
定义2.3 设f:(X,τ)→(Y,δ)是两个拓扑空间之间的映射.若f满足:对任意B∈δ,有f←(B)∈τ,则称f是连续映射.
命题 2.4(连续映射的邻域刻画)
设f:(X,τ)→(Y,δ)是两个拓扑空间之间的映射,则f连续当且仅当对任意x∈X,若B是f(x)的邻域,则f←(B)是x的邻域.
设(P,≤)是一个预序集,D⊆P,若D≠Φ且对任意d1,d2∈D,存在d3∈D使得d1≤d3,d2≤d3,则称D是一个定向集.
定义 2.5 设(X,τ)是一个拓扑空间,(D,≤)是一个定向集,则称映射S:D→X是X的一个网.
定义2.6 设(X,τ)是一个拓扑空间,U⊆X,x∈X,S:D→X是X的一个网.若任给x的邻域U,存在d∈D,当n≥d时,有S(n)∈U,则称S收敛到x,记为S→x.
三、可度量化拓扑空间中的邻域
在数学分析中,邻域是一个非常重要的概念.在一维欧氏空间中,U是x的一个邻域是指:存在r>0,使得B(x,r)⊆U,其中,B(x,r)={y||x-y| 定义3.1 若一个拓扑空间可以由一个度量空间导出,则称拓扑空间是可度量化的. 根据度量空间诱导拓扑空间的具体过程可知,如果拓扑空间τ是可度量化的,则存在度量d使得开球族{Bd(x,r)|x∈X,r>0}是τ的基,其中Bd(x,r)={y∈X|d(x,y) 命题3.2 设τ是一个可度量化空间(τ=τd),则U是x的一个邻域当且仅当存在r>0使得Bd(x,r)⊆U. 众所周知,在实数集R上赋予度量d(x,y)=|x-y|,则(R,d)是一个度量空间,进而诱导一个拓扑空间(R,τd),称为标准拓扑空间.由命题3.2可知,(R,τd)中邻域的概念恰好是数学分析中学习的实数集中的邻域的概念.实际上,数学分析中介绍的实数集中的邻域推广到拓扑空间背景下,对应的是可度量化拓扑空间中的邻域. 教师通过这一讲解过程,就明确了数学分析中介绍的邻域跟一般拓扑学中讲的邻域之间的联系.由于可度量化拓扑空间中的邻域依赖于其基元素,即由度量诱导的开球.因此,教师还应该帮助学生加深对可度量化拓扑空间中开球的认识.为此,教师可以引导学生探索Bd(x,r)的具体几何特征.受到数学分析中理解开球的思维的影响,许多学生主观认为Bd(x,r)的图形就是一个球(或圆)的形状.实则不然.以二维欧式空间为例,在R2上存在大家广为熟知的两个度量,如下: ∀x=(x1,x2),y=(y1,y2)∈R2, d2(x,y)=max{|x1-y1|,|x2-y2|}. 容易验证d1和d2诱导出R2上相同的拓扑,即由d1和d2诱导的开球都可以作为R2上的度量拓扑的基元素.但通过作图我们可以看出,Bd1(0,1)是一个圆形区域,而Bd2(0,1)是一个正方形区域. 因此,教师在讲解可度量化拓扑空间中的邻域时,要向学生强调可度量化拓扑的基元素的具体几何特征,加深学生对这些抽象概念的直观认识,帮助学生跳出数学分析中的通常的开球形状的束缚,以此辅助学生更好地理解不同的度量意义下的开球的形状是不同的,但可能会诱导出相同的可度量化拓扑.教师还非常有必要指出,因为一般的拓扑空间并没有开球形式的基元素,故一般的拓扑空间中的邻域,不能像可度量化拓扑空间的邻域,可以包含一个度量诱导的开球,这也是可度量化拓扑空间和一般的拓扑空间的一个区别之处. 在一般拓扑学中,连续映射反映了两个拓扑空间中开集的关系,这是联系两个拓扑空间的重要桥梁.一般拓扑学教材通常是直接给出连续映射的抽象定义,即开集的原像是开集.这对于刚开始接触一般拓扑学的学生来说,只能先去硬性地接受这一概念,后续再纯粹从理论推导的角度加强对这一概念的认识.在数学专业学生考研面试环节,学生经常被问到一般拓扑学中的连续映射和数学分析中的连续映射有什么联系.针对这样的问题,如果不对连续映射做进一步的解释,学生很难深入理解到两门课程中提到的连续性的关系.那么,教师如何才能从学生更熟悉和更容易接受的角度讲解这一概念呢? 数学分析通常是利用ε-δ语言定义一个函数f在某点x0处的连续性,具体如下: ∀ε>0,∃δ>0,当|x-x0|<δ时, |f(x)-f(x0)|<ε. (1) 若f在每一点x0处都是连续的,则称f是整体连续的.在一般拓扑学通常是利用开集的原像是开集定义一个映射的整体连续性.形式上二者差别很大,初学者很难自己去发掘它们之间的联系.为了帮助学生梳理清楚两者之间的关系,教师需要先讲解一般拓扑学中一个函数在单点处的连续性,利用拓扑空间中的邻域概念,可以定义一个映射f:(X,τX)→(Y,τY)在x0处的连续性: 对任意的f(x0)在(Y,τY)中的邻域B, f←(B)是x0在(X,τX)中的邻域. (2) 我们进一步可以证明,若映射f:(X,τX)→(Y,τY)在每一点x0处都连续,则映射f:(X,τX)→(Y,τY)是整体连续的.容易看出,数学分析和一般拓扑学中映射的整体连续都可以通过逐点连续刻画.因此,为了帮助学生理解两门课程中连续映射的关系,教师只需要将两者的逐点连续的关系梳理清楚,即只需将(1)和(2)的关系梳理清楚即可.考虑实数集R上拓扑问题时,我们通常采用的是标准拓扑,即以度量d(x,y)=|x-y|诱导的拓扑τd.此时,我们将(2)中定义连续映射的方式应用于映射f:(R,τd)→(R,τd).这样定义的f:(R,τd)→(R,τd)的连续性和(1)中的ε-δ方式定义的连续性是等价的. (1)⟹(2):若B是f(x)在(R,τd)中的邻域,由命题3.2可知,存在ε0>0,使得Bd(f(x0),ε0)⊆B.由(1)可知,对上述ε0,存在δ0>0,使得|x-x0|<δ0时,|f(x)-f(x0)|<ε0.所以,当x∈Bd(x0,δ0)时,f(x)∈Bd(f(x0),ε0),即当x∈Bd(x0,δ0)时,x∈f←(Bd(f(x0),ε0)).从而有Bd(x0,ε0)⊆f←(Bd(f(x0),ε0)).因此,f←(B)是x0在(R,τd)中的邻域. (2)⟹(1):对任意的ε>0,则Bd(f(x0),ε)是f(x0)在(R,τd)中的一个邻域.由(2)可知,f←(Bd(f(x0),ε))是x0在(R,τd)中的邻域.由命题3.2可知,存在δ>0,使得Bd(x0,δ)⊆f←(Bd(f(x0),ε)).所以,当|x-x0|<δ时,即x∈Bd(x0,δ0)时,必有x∈f←(Bd(f(x0),ε)).从而f(x)∈Bd(f(x0),ε),即|f(x)-f(x0)|<ε.综上,对任意的ε>0,存在δ>0,当|x-x0|<δ时,|f(x)-f(x0)|<ε. 经过上述分析我们可以得出结论,数学分析中学习的实数集上的函数的连续性恰好等价于该函数在实数集上的标准拓扑意义下的连续性,从而帮助学生从一般拓扑学的角度对数学分析中学习的函数的连续性概念增加全新的认识和理解,辅助学生梳理一般拓扑学和数学分析两门课程的联系. 数列的收敛在数学分析中起到至关重要的作用,而且数列的概念可以很自然地推广到拓扑空间中.因为拓扑空间的邻域是一般的集合,故数列被推广到拓扑空间中之后,被称为序列,即以正自然数集标号的一个集合{xn|n∈N+}.借鉴数学分析中数列收敛的定义方式,在一般的拓扑空间中,以邻域为工具,我们可以自然地给出序列{xn}收敛到x的定义: 若对x的任一邻域U,∃N0∈N+, 当n>N0时,xn∈U, 通常记为{xn}→x. 但序列收敛在一般的拓扑空间中并不能发挥像数列收敛在实数集中发挥的那样的作用.比如,数学分析中的归结原理: 设f:R→R是一个映射,则有 f:R→R是连续映射当且仅当对任意的数列{xn},{xn}→x蕴涵{f{xn}}→f(x). 在一般的拓扑空间中,若将上述结论中的数列替换为序列,必要性仍然成立,但充分性不再成立.从中可以看出,序列在一般的拓扑空间中起到的作用跟数列在实数集中起的作用是有区别的.因此,教师应该跟学生强调,序列并不是数列在一般的拓扑空间中应该对应的概念.针对这一问题,我们需要在拓扑空间中引入新的概念,作为数列的对应概念.此概念恰好就是拓扑空间的网(见定义2.5),并且数列的收敛恰好对应于网的收敛(见定义2.6).我们借助网和网的收敛,得到一般的拓扑空间中的原理: 设f:(X,τX)→(Y,τY)是两个拓扑空间之间的映射,则有 f:(X,τX)→(Y,τY)是连续映射当且仅当对任意(X,τX)中的网S,S→x蕴涵f(S)→f(x). 从中可以看出,在一般的拓扑空间中,用网替换数列更为合理.当然,除了归纳原理,还有很多拓扑空间中的概念和性质讨论利用网才能得到更好的结果,比如,刻画聚点,闭包,分离性等.总之,在一般的拓扑空间框架下,网才是数列的合理推广.在这一讲解过程中,教师要有意识地培养学生从一般拓扑学的角度理解数学分析的思维模式,而且引导学生寻找熟悉的数学分析中的概念在一般的拓扑空间中的对应.教师通过这一过程,帮助学生总结数学分析和一般拓扑学课程相通的知识点,一定要注意着重分析可能存在的区别. 从上述讲解过程中,我们可以看出序列不能作为数列的完美的推广形式,但这不意味序列及其收敛在拓扑空间中没有意义.我们借助序列可以描述和刻画拓扑空间的很多性质,而且,当拓扑空间满足第一可数公理时,序列收敛和网的收敛是等价的.因此,考虑第一可数空间的相关问题时,我们可以优先选择序列,因为在形式上序列要比网更为简洁,利用起来更为方便. 一般拓扑学是数学分析和实变函数等多门分析学课程的延伸,最显著的特点是将公理化的研究方法与具体的数学性质相结合.通过一般拓扑学课程的学习,我们可以更好地梳理多门分析学课程的内在联系.如果从一般拓扑学的角度看待数学分析,学生可以将数学分析课程中的诸多基础概念理解得更加透彻.教师结合一般拓扑学的抽象化特点,结合抽象的拓扑概念,对数学分析中的具体概念加以解释,可以帮助学生从一个更高的层面去理解和解释数学基础课程中的概念和性质.在考研背景下,教师借助一般拓扑学课程,可以帮助学生串联和梳理各门相关课程之间的关系.对一般拓扑学的学习,不仅可以帮助学生加深对各门相关课程的理解,还可以辅助数学专业学生从容应对考研复试中的面试环节.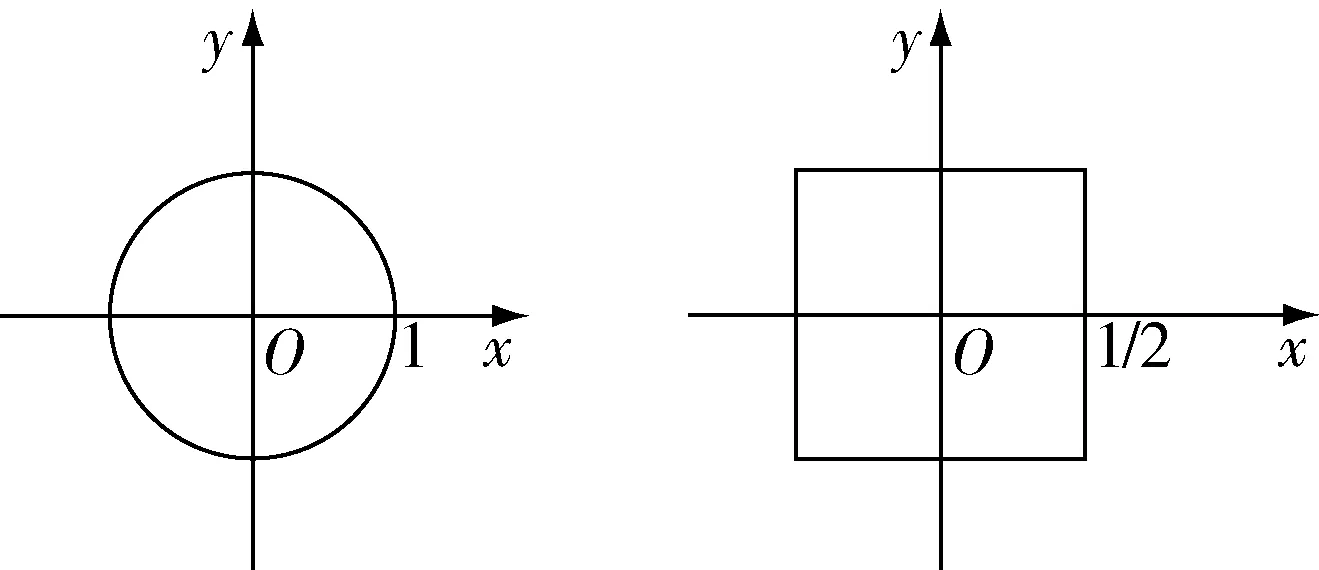
四、拓扑空间之间的连续映射
五、序列和网
六、总 结

