数形结合思维与高中物理解题教学的有机结合

刘芬

摘要：高中物理解题教学中，运用数形结合思维能够帮助学生快速清晰地理清解题思路，找到解题的突破点.文章以具体的高中物理习题，阐述了数形结合思想在高中物理解题教学中的应用思路和具体途径，以期起到以点带面、举一反三的效果，帮助高中物理教师探索一条有效的解题路径.

关键词：数形结合;高中物理;解题教学;策略

中图分类号：G632文献标识码：A文章编号：1008-0333（2022）16-0094-03

在新课改的教育背景下，跨学科的学习理念得到广泛的应用，为高中物理学科的解题教学提供了良好的助力作用.其中，数学学科的数形结合思想在高中物理应用的频率较高.巧妙应用数形结合思维，可以迅速找到破题点，帮助学生精准、快速的求解出题目的答案.

1 数形结合思想在高中物理解题教学中的应用思路

1.1 借助图形，解决物理问题中的数量关系

以形助数是数形结合思想常用的思路.换言之，需要学生从图形入手，通过细致的绘图，将抽象复杂的物理习题转变成直观易懂的图形.从中找出解题思路，总结规律，顺利得出问题的答案.对此，物理教师在解题教学时需要通过草图来为学生分析已知条件和未知量之间的关系，将文字描述转化成学生熟悉的物理公式.

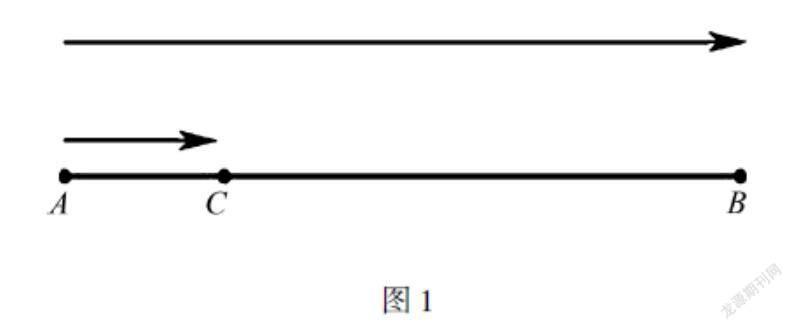
比如例题：某名初中生在百米练习时，他的一位朋友在终点帮忙计时，当朋友听到了枪声时按下了计时钮，看到学生跑到终点时停止计时，时间为13s，试问这个朋友的计时方式是否正确？如果不正确，这个学生的真实成绩应该是多少秒？（假设是直线跑道，声速为340m/s）

许多学生在初次解答这类习题时，常常分不清声音传播的时间应该包括在运动过程当中，还是要独立看成一个部分.因此在解题时，很容易将题目中的条件弄混淆.通过数形结合的思想，教师可以先绘制草图，将题干中的条件标记在草图上.用图形来表示数字，帮助学生理清其中的数量关系.如图1所示，上方的草图是枪声响起的那一刻，初中生的跑步过程.下方的草图是计时员记录的跑步过程.由于声音传播需要一定的时间，当初中生的朋友听到枪声时，初中生已经从起点A点跑到了C点的位置，此时才是他朋友按下计时钮的时刻.因此，通过草图的分析，不难发现从C到B才是题干中13s的时间.综上所述，根据公式t声=S/v声，求出声音传播的时间大约为0.3s，再与原来的时间相加，得出13.3s才是初中生正确的跑步时间.由此，通过以上数形结合的解题过程，这道题的疑问都能迎刃而解.

1.2 通过数量关系，分析复杂的图形

有正必有反，数形结合既可以从形到数，也可以由数到形.某些物理习题通常会给出一张示意图，让学生根据图像来解决其中的物理问题.通过静态的图片，学生很难想象出其中的物理规律.这就需要从图形体现的数量关系上入手，剖析其中的内涵.

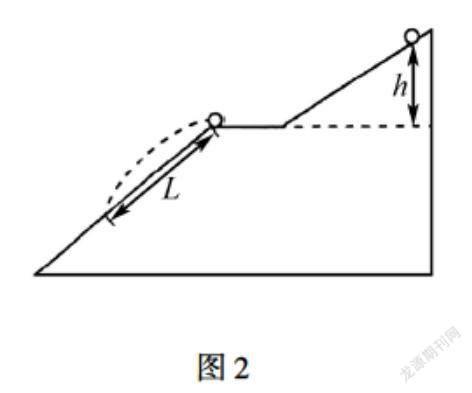
比如习题：根据图2所示，有一个小球沿着某个光滑斜面从静止状态开始滚落，在平面上滚动一段距离后进入平抛运动的状态.根据数据统计后发现，斜面的竖直高度h与平抛运动距离L存在一定的关系，假设小球不受碰撞、摩擦力的影响，试问L和h之间的运动关系.

2 数形结合思想在高中物理解题教学中的应用途径

2.1 物理力学问题

力学是高中物理的基石，关于重力、摩擦力、合力、共點力等力学领域的物理知识，经常需要绘制示意图，来剖析力与力之间的数量关系.此外，与力学相关联的物理知识也非常广泛，比如前文引用的运动学例题，以及生活中常用的牛顿定律，均与力学有着密切的内在联系.因此，学生学会在力学问题中应用数形结合思想，对于该思维和物理解题之间的融合可以起到良好的促进作用.

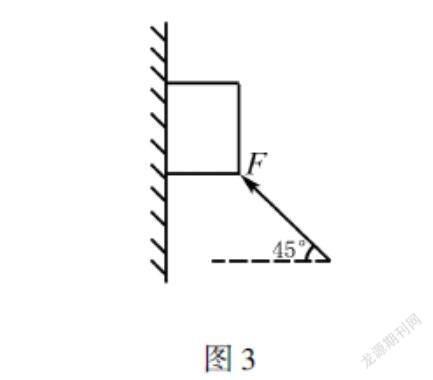
比如习题：如图3所示，某个重为G的木块与竖直墙壁的动摩擦系数为μ，如果以大小为F的推力推动木块匀速上滑，F的角度与水平面成45°夹角，试求F的大小.

对于这道力学问题，可以发现其中涉及的力学因素比较复杂，有摩擦力、推力、重力分别施加在木块上.如果从每个力单独进行考虑，解题思路将十分繁琐.对此，利用正交分解法绘制坐标图，再应用数形结合思想求出力与力之间的关系，可以迅速求解出答案.

力学题目的难度通常跨度较大，做题难度在学生心中呈现两极分化的感想.有些空间感觉优秀、逻辑思维较强的学生，能准确判断力的性质，在脑海中构思出合力的方向.而另一些空间感较差、逻辑思维能力不足的学生，则无法通过凭空想象的方式，找出力学题目的解题思路.对于这一类学生，数形结合思想可以成为促进学生思维活力的内驱力，帮助学生梳理好多个作用力之间的复杂关系.同时，这也能帮助学生将物理知识与数学三角函数知识联系在一起，实现学科联合的教学目的.长此以往，高中生就会在潜移默化中找到理科课程之间的联系点，从而促进学生跨学科学习品质的全面进步.

2.2 物理电学问题

电学也是物理学习的难点，许多学生通常对电学知识抱有错误的理念，认为电学的学习重点在于电路图的组装上，需要在实践中投入更多的学习精力.但电学的计算问题也比较繁琐，许多电学公式经常需要与图象来综合应用，才能顺利的解答相应的例题.因此，电学问题也是数形结合思想经常应用的途径之一.

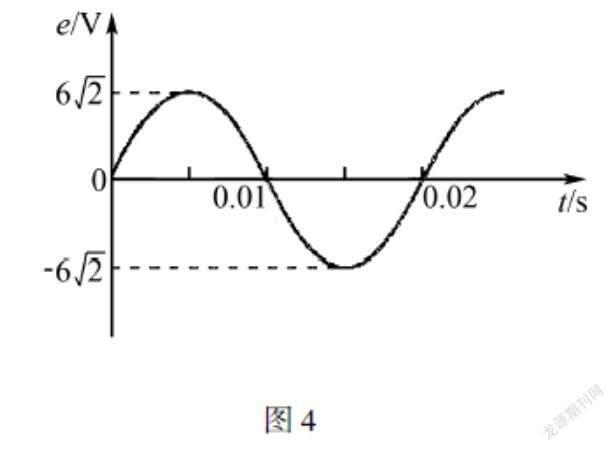
比如例题：已知某架发电机的电动势e与t的关系图像如图1所示，试求以下问题：1、在什么时间，发动机的电动势为0？2、如果在发电机上连接电压表，电压表的示数为多少？3、如果继续在发电机上外接一盏灯泡，灯泡的电阻为9Ω，问这盏灯泡消耗的功率为多少？

2.3 物理实验问题

实验题是高中物理学科的重要组成，不仅在实践方面要求学生熟练掌握实验的操作过程，也是物理考试的常客之一.对于实验课程，高中生既需要重视动手实践，也要根据实验图像来准确的分析、整理数据.因此，学生需要着重锻炼绘图的能力，能将实验的数据以表格、坐标图的形式直观的表现出来，体现实验与图形的有机结合.

2.4 物理运动习题

运动类物理习题历来是高考的热门题型，是学生必须掌握的重点知识.这一类题目的解答难度较高，尤其一些有关“速度与时间”“加速度与时间”“位移与时间”的运动题，部分学生在解答的过程中常常会出现张冠李戴的情况，将有关运动的公式错误套用.为了帮助学生突破这一学习难关，提高做物理运动题的正确率，教师可以通过数形结合的方法，深入解析运动图像，帮助学生弄懂图像中每个部分都代表什么，具有什么样的含义.由此，才能有效防止学生弄混知识点.

例如：小明在物理课上做了一个实验，实验内容为利用加速度传感器，研究某个物体从静止做直线运动的变化情况，已知该物体的质量m为1kg，且得出一张有关“加速度和时间”的图像，如图5所示.针对该图像，以下说法正确的是：

1.当时间t=10s时，此时物体的速度大约为6.8m/s.

2.当时间t在2s至6s之间时，这个物体受到的合外力处于先增大再减小的变化特点.

3.当时间t在4s至6s之间，该物体的运动特点为匀速直线运动.

通过长期的教学实践，可以发现数形结合思维在高中物理解题教学中具有极高的应用价值.物理教师应当细心筛选经典例题，帮助学生扎实的掌握“以数解形”与“以形助数”两种数形结合思路，深入体会数形结合思维在高中物理解题中的实用性.

参考文献：

[1] 贾剑，何纪达.数形结合，突破物理解题困境[J].高中数理化，2021（02）：35-36.

[2] 韩冰.例析数形结合思想在高中物理解题中的应用[J].中学生数理化（自主招生），2020（04）：33.

[责任编辑：李璟]