与时间相关的非线性抛物型方程的反源问题

王泽慧

(兰州交通大学 数理学院,甘肃 兰州 730070)

0 引言

近年来，许多学者对具有物理背景的偏微分方程进行了大量的研究[1-5]，这些研究绝大部分是针对正问题展开的，即研究解的存在性、唯一性以及稳定性.随着科学技术的发展，实际应用领域提出了很多由果索因的问题，这些问题的一大特点是系统中的部分参数或状态是未知的，这就是所谓的反问题.反问题的研究近年来在科学和工程的各个分支中起着越来越重要的作用，但是由于其不适定性，反问题的研究难度较正问题而言会更大些.本文所研究的反问题是对一个非线性抛物型方程在给定的积分附加条件下进行源项重构.

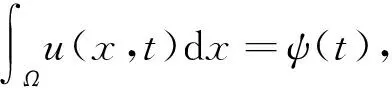
本文结构如下：首先，由于源项是仅与时间相关的，并且附加条件是与空间积分相关的，所以文章将原方程进行空间积分, 再将方程中的q(t)替换得到了与原问题等价的反问题, 随后证明了该反问题解的唯一性、弱解存在性并且导出了误差估计.

1 解的唯一性

本文研究了一类非线性抛物型方程的源项重构问题,模型为

(1)

其中：r(x),u0(x) 都为已知的光滑有界函数；k(u)为已知的非线性函数,且Lipschitz连续(不失一般性，假设k(0)=0)；q(t)是方程的未知源项系数；假设给定附加条件：

其中：ψ(t)为已知函数.本文将要讨论如何根据上述信息来确定函数u和q.

为了便于研究问题(1),以下对区域Ω上任意给定的函数u,v定义L2内积以及范数分别为

引入测试函数空间：

V={φ:Ω→R;φ|∂Ω=0,
‖φ‖+‖∇φ‖+‖Δφ‖+
‖∇φ·n‖∂Ω<∞},

其中：n为边界外法线向量.

对问题(1)中的偏微分方程在x∈Ω上进行积分，得

将(1)中的第一个方程与测试函数-Δφ相乘,在Ω上进行积分,且对第一项应用格林公式,有

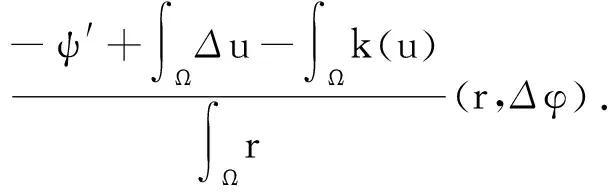
(2)

接下来需要证明：如果这个变分问题有解,那么解是唯一的.

引理1假设r∈H1(Ω),ψ′∈L2(0,T),u0∈V，对∀s有|k(s)|≤C(|s|+1)，则存在C>0,使得以下不等式成立,

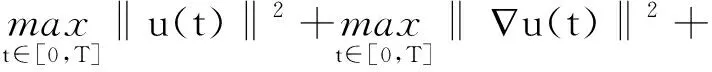
证明令φ=u，并且在时间(0,t)上进行积分，可以将式(2)写为

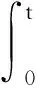
(3)

显然,等式(3)左侧第一项可写为

由|∂Ω|>0以及Friedrichs不等式[ 9],有

‖u‖≤C‖∇u‖.

由于|k(s)|≤C(|s|+1)，利用Friedichs不等式可将式(3)左侧第二项化为

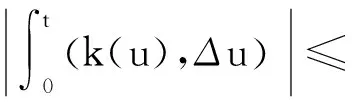
对任意的函数z∈H1(Ω),以下不等式成立，

相应地,以下不等式也成立，

应用格林公式、r的正则性、Young不等式、Friedrichs不等式以及上式，可将式(3)右侧项化为

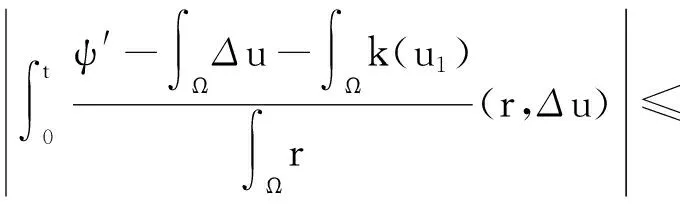
整合以上不等式，同时考虑ε和η，使得ε+Cε·η足够小，则对∀t∈[0,T]，有

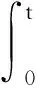
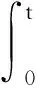
应用Gronwall不等式即可得证.

注条件|k(s)|≤C(|s|+1)并不难满足.事实上，当k(s) Lipschitz连续,且k(0)=0时,有

|k(s)|≤|k(s)-k(0)|≤L|s|,

L>0是Lipschitz常数,故上述条件显然成立.

定理1假设r∈H1(Ω),ψ′∈L2(0,T),u0∈V,那么变分问题(2)最多存在一个解.

证明假设变分问题(2)有两个解u1,h1和u2,h2.令u:=u1-u2,h:=h1-h2.将两个解分别代入式(2)进行相减,用u代替φ,并且在时间上进行积分得

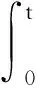
(4)

对等式左侧第三项,应用Friedrichs不等式以及Young不等式，有

(k(u1)-k(u2),Δu)≤
‖k(u1)-k(u2)‖‖Δu‖≤
C‖u‖‖Δu‖≤C‖∇u‖‖Δu‖≤
Cε‖∇u‖2+ε‖Δu‖2.

与引理1同理，等式(4)右侧项可化为

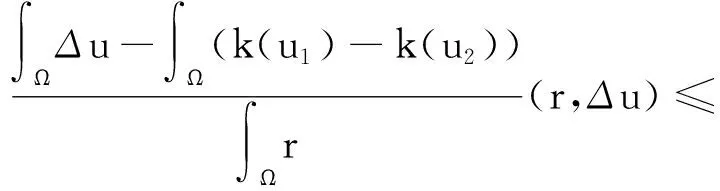
将以上估计整合到一起.对任意的t有

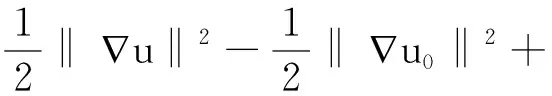
同时考虑ε和η,使得ε+η·Cε足够小,对∀t∈[0,t]，有

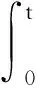
应用Gronwall不等式得u=0,同时q=0,即u1=u2,q1=q2，证毕.

2 解的存在性

2.1 时间离散格式

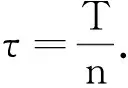
此时,对式(2)进行离散化,得到如下逼近方案

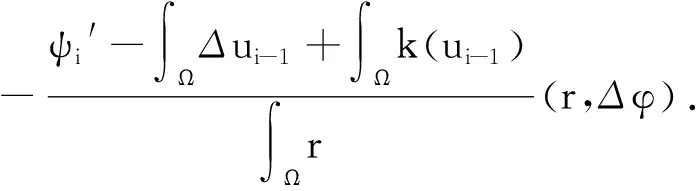
(5)

引理2假设r∈H1(Ω),ψ′∈C([0,T]),u0∈V,对于∀i∈{1,…,n},都存在唯一的(ui,hi)满足式(5).

证明显然,可将式(5)写为

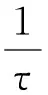
(6)

根据引理1,由r的正则性,k(u)的Lipschitz连续性以及Hölder不等式,有

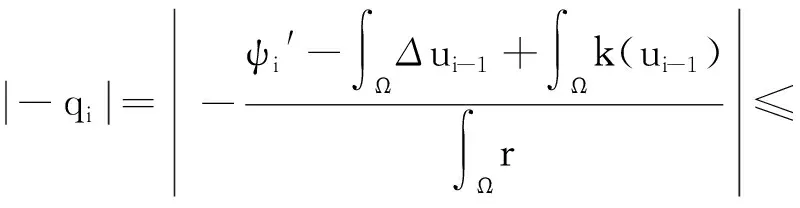
对于式(6)右侧三项，分别可做以下估计，

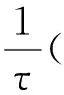
对上述估计进行整合，可得

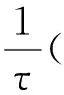
等式左侧表示V×V上的一个椭圆、连续、双线性形式,等式右侧是Hilbert空间V上的线性有界泛函.根据 Lax-Milgram定理[10],利用线性椭圆偏微分方程理论可得解的存在唯一性.

接下来进行(ui,hi)的稳定性分析.

引理3假设r∈H1(Ω),ψ′∈C([0,T]),u0∈V,则存在C和τ0,使得对∀0<τ<τ0,有

证明令φ=uiτ,并对i进行连加,则可将式(5)写为

(7)

等式(7)左侧第一项有

根据引理1,利用Cauchy不等式、Young不等式、迹定理、以及Friedrichs不等式,可将等式(7)右侧第二项化为

进一步,利用Cauchy不等式和Young不等式将等式右侧第一项化为

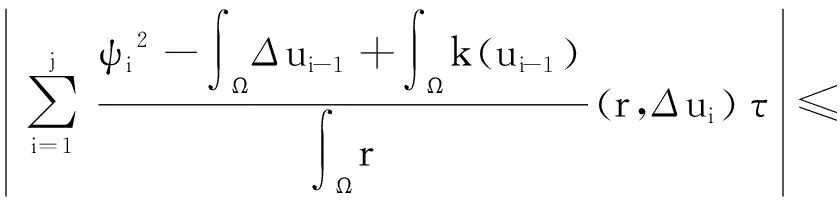
将以上估计整合,得

同时取足够小的ε和η使得ε+η·Cε足够小,利用Gronwall定理,可得证.

引理4假设r∈H1(Ω),ψ″∈L2(0,T),u0∈V,则存在C和τ0，使得对∀0<τ<τ0，有

证明在式(5)中,令φ=δuiτ,并对第i项进行连加,得

(8)

显然,等式(8)左侧第二项可写为

根据引理2,利用Hölder不等式、Young不等式, 可将等式(8)右侧第一项化为

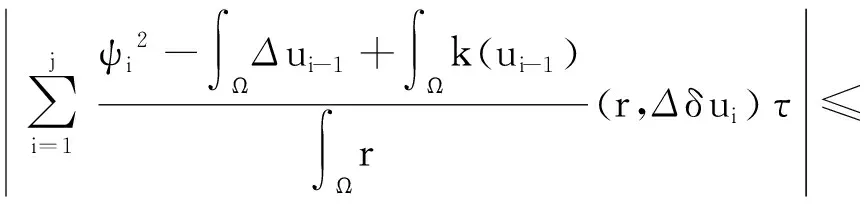
同时,可将等式右侧第二项化为

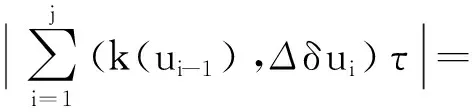
对上式进行整合，可得

取ε足够小,则有

(ii)由引理2得

|qi|≤C(|ψi′|+‖Δui-1‖+‖ui-1‖)≤
C(‖Δui-1‖+‖ui-1‖)，

则

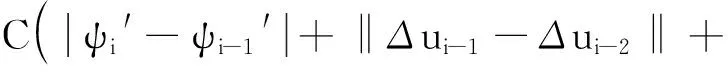
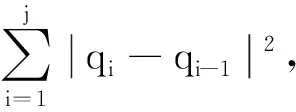
而由引理3得

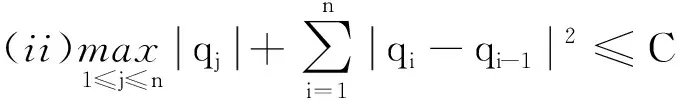
2.2 弱解的存在性

引入分段线性时间函数un：

un(0)=u0,un(t)=
ui-1+(t-ti-1)δui,t∈(ti-1,ti].

定义阶梯函数：

使用新的记号可将变分公式(4)写为

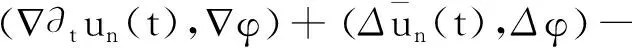
(9)

定理2假设r∈H1(Ω),ψ″∈L2(0,T),u0∈V,则式(1)存在一组解(u,h),其中

u∈C([0,T],L2(Ω))∩L∞((0,T),V),

∂tu∈L2((0,T),H1(Ω)),q∈L2(0,T).

证明(i)由引理3、4得

由文献[10]可知，存在

u∈C([0,T],L2(Ω))∩L∞((0,T),V)

和子序列{un}，满足

其中u是时间可微的且在[0,T]中处处收敛.

∂tun⇀∂tu,t∈L2(0,T),u∈H1(Ω).

由于

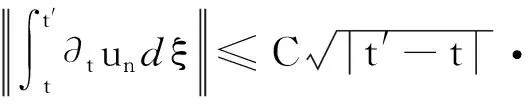
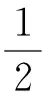
类似地，可以得到

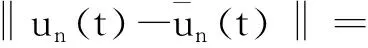
和

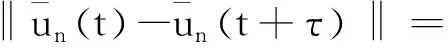
则有

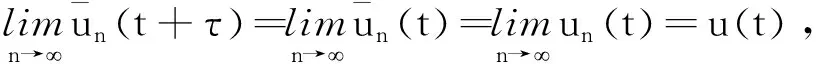
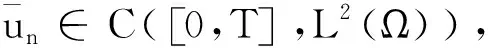
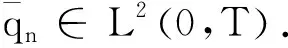
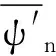
当τ→0时，可得

接下来，对于∀t∈(ti-1,ti)有

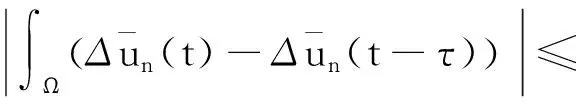
根据引理4(i)，可得

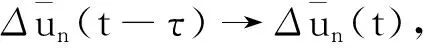
同理，根据k(u)的Lipschitz连续性、Friedrichs不等式以及引理3，可得

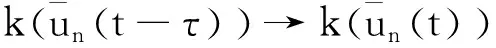
(iii)对式(3)在时间上进行积分得

上式对n取极限,有

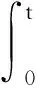
对上式进行微分,且对第一项应用格林公式,得

-(∇∂tu,Δφ)+(Δu,Δφ)-
(k(u),Δφ)=-q(r,Δφ)，

即得

∂tu-Δu+k(u)=qr，

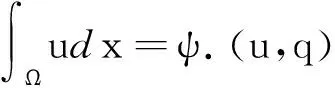
3 误差估计

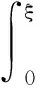
(10)

定理3假设r∈H1(Ω),ψ″∈L2(0,T),u0∈V,则存在一个常数C，满足

证明首先,对等式(10)左侧的第一项有

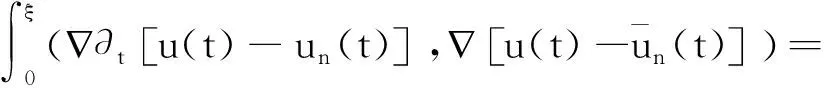
利用Cauchy不等式和Young不等式,对等式(10)右侧的第一项可做以下估计

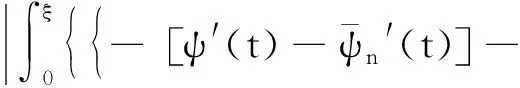
接着,对等式(10)右侧第二项做以下估计,

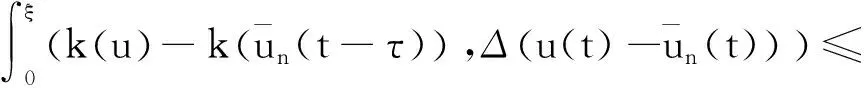
将上述估计整合起来,并取足够小的ε,则有

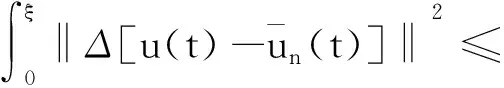
应用Gronwall不等式即可得证.

4 结语

本文研究了一个具有未知源函数的非线性抛物型问题.通过给定的积分附加条件对方程进行等价改写，定理1证明了改写后所得到的变分公式其解的存在唯一性；接着基于向后欧拉方法对变分公式进行了时间离散化，引理3及引理4导出了一系列先验估计，同时定理2说明了变分问题解的存在性；最后，定理3对所研究的近似方法进行了误差估计.