基于自适应Levy飞行的黄金正弦可见光定位研究

张慧颖,王 凯,于海越,牟 昊

(吉林化工学院 信息与控制工程学院，吉林 132022)

引 言

21世纪以来，随着智能通信与无线网络的发展，全球定位系统(global positioning system,GPS)广泛应用于室外定位服务，并具有很高的定位精度[1]。室内电子设备存在电磁干扰GPS在室内无法实现高精度定位[2]。室内可见光定位图像传感器的定位系统，利用几何成像实现定位功能，但存在设备复杂、定位速度慢的问题[3]。目前依托于发光二极管(light-emithing diode,LED)灯作为发射端的可见光通信(visible light communication，VLC)技术[4]，在室内定位中有更高的抗干扰性。现有的室内定位距离计算的方法包括信号强度指示(received signal strength indication，RSSI)[5]、通过到达角度(angle of arrival,AOA)[6]、到达时间差(time difference of arrival，TDOA)[7]计算距离。参考文献[8]中将AOA和RSSI相结合提出一种室内混合定位算法，误差在10cm左右，但混合两种算法复杂度和成本都比较高。参考文献[9]中将PSO和BAS两种算法结合起来大大降低定位的复杂性，但定位的精度有待提高。参考文献[10]中针对传统的PSO算法进行优化，测试点的平均定位误差大约为5cm。参考文献[11]中使用3个LED灯兼顾室内照明的同时进行室内定位，但定位误差低于10cm定位精度还有待提高。参考文献[12]中将RSSI/TDOA两种定位技术混合进行定位，定位精度有提高，但存在定位过程复杂、速度较慢的缺点。由于传统黄金正弦算法存在易陷入局部最优，定位精度低的问题。

本文中提出基于自适应Levy飞行的变异机制改进黄金正弦算法，根据RSSI通过朗伯模型得到未知节点与参考节点的距离，改进后的黄金正弦算法对目标位置不断寻优进行精确定位。仿真结果表明，改进黄金正弦定位算法与其它定位算法相比定位速度更快、精度更高。

1 RSSI室内可见光定位技术

LED灯将接收到的电信号转化为光信号进行传输，光电二极管(photo diode,PD)将接收到的光信号转化为电信号，使用空间角度和光强度的关系表示朗伯光源的光强分布[13-14]。参考文献[15]中通过计算得出光信号反射次数为3次～10次时对系统的影响可以忽略不计，由于室内情况复杂漫反射为主要反射源，大部分反射信号需3次及以上反射才能被PD接收端接收。因此本文中只考虑直射链路，对反射信号忽略不计。

在10m×10m×3m的室内空间中设置9盏LED灯作为信号发射器，将其呈等间隔对称分布安装在距离地面3m的天花板上。将PD作为接收器安装在移动端上。LED发射器和接收器定位系统模型如图1所示。

Fig.1 Indoor visible light positioning model

接收光功率Pr与发射端功率Pt的关系为：

Pr=H(0)Pt

(1)

式中，H(0)为信道增益，信道增益可以表示为[16]：

H(0)=

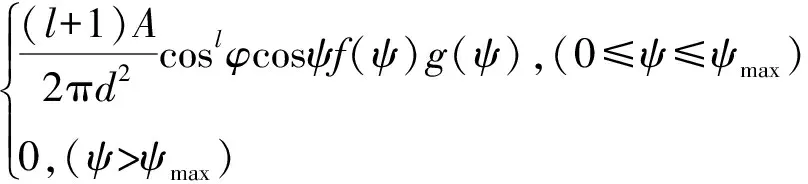
(2)

式中，A为PD的面积;d为LED到PD的相对距离;φ为发散角;ψ为接收角;ψmax为PD最大视场角;f(ψ)为PD的光滤波器增益；g(ψ)为聚光器增益。将(1)式和(2)式联立即可推导出LED与PD间的距离d;l为朗伯散射系数，朗伯系数大小由LED灯的半功率角ψ1/2决定:

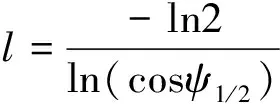
(3)

LED发光强度模型如下[17-18]:

Iθ=I0coslψ

(4)

式中,Iθ为发射角θ的发光强度；I0为垂直于发光面的发光强度。

RSSI定位是根据PD接收到来自多个发射器发出的光源信号强度得到欧氏距离，利用三边法求解出目标位置的对应坐标点。已知参考点与待测节点坐标，代入三边定位算法公式可计算出3个圆心到达待测点的距离d。由于室内充斥着电磁的干扰，三边测距法计算3个圆不会理想地交于一点,因此通过黄金正弦算法寻找最优解。

2 改进黄金正弦定位算法

2.1 传统黄金正弦算法

黄金正弦算法(golden sine algorithm,Gold-SA)是一种新型元启发式算法[19-20]。黄金正弦算法是在正弦函数上沿着同一搜索路线，将单位圆上的每一个点访问一遍，当位置更新时加入黄金分割率进而去缩小解的范围，使得区域范围更小，进而可以提升算法搜索速度。Gold-SA算法在更新个体位置时，引入黄金分割率，分别设系数x1和x2,将系数加入到位置更新公式中，缩小搜索空间使得寻优速度更快，黄金分割系数x1和x2为：

(5)

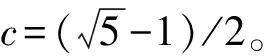
黄金正弦算法中结合黄金分割率的系数，在搜索空间中寻找最优解，其位置更新公式为[21]：

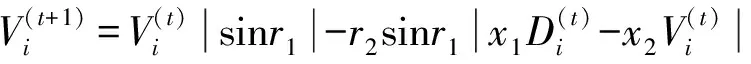
(6)

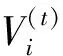
2.2 改进黄金正弦算法

本文作者提出将Levy飞行变异机制结合自适移动因子改进黄金正弦算法，对位置更新公式进行变异，提高算法种群的多样性，能够快速跳出局部最优。Levy飞行机制的核心是短距离游走和长距离跳跃交替变化，当处于短距离游走时种群的多样性将会提高，处于长距离跳跃时种群搜索具有方向的多样性，搜索更为详细[22-23]。L为Levy飞行的移动步长参数，计算公式为：

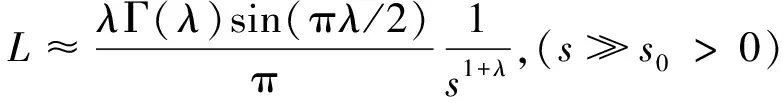
(7)

式中，λ为缩放因子，参考文献[24]中建议取λ=1.5；Γ(λ)为标准的伽玛函数；s为移动步长；s0为起始步长，即s>>s0>0为s→∞。

在黄金正弦算法全局搜索中引入Levy飞行变异机制帮助算法跳出局部最优，但Levy飞行变异机制无法满足算法需要较高的收敛速度。本文中提出Levy飞行机制结合自适应移动因子对黄金正弦算法位置更新公式改进，进而提高算法的收敛速度。自适应移动因子α的公式为：

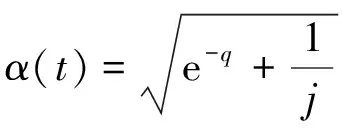
(8)

式中，j为当前的迭代次数；q=1+j/M，M为最大迭代次数。

使用Levy飞行变异机制结合自适应移动因子对Gold-SA位置更新公式进行变异，变异后的位置更新公式为：

αL(m,n)×(xbest-xi)

(9)

式中，L(m,n)是关于多个未知量下的步长参数的矩阵，其中m表示控制常数，n为未知量个数，取m=1.5,n=3;xbest表示每次迭代最优解矩阵;xi表示当前迭代得出的解的矩阵。

基于Levy变异机制改进Gold-SA算法实现室内可见光定位的流程如下:(1)PD接收器接收LED光信号，计算出LED与PD间的距离d;(2)设计初始种群个体数为N,最大迭代次数M,空间维数D的初始种群;(3)计算每个个体的适应度的值Pbest，并将最优个体对应的适应度值存入xbest;(4)根据(9)式更新个体的位置;(5)更新个体，比较个体的适应度值取出最佳适应度值个体作为下一次迭代的解;(6)判断是否已经达到设置迭代次数，若达到则结束，若未达到则转向第(4)步;(7)得到全局最优解。

3 仿真与结果分析

3.1 可见光定位算法仿真对比分析

选取体积为10m×10m×3m的室内空间作为仿真测试空间，设置9盏LED灯按照3×3的网格排列方式排布。在室内随机放置一个待测点，分别选取最小二乘(least square mathod,LMS)的RSSI定位算法、PSO的RSSI定位算法、Gold-SA的RSSI定位算法和改进的Gold-SA的RSSI定位算法，比较各算法定位产生的定位误差。设置PD有效接收面积为1cm2。仿真参量表如表1所示。

Table 1 Simulation parameters

Fig.2 Algorithm error comparison

在3维空间中分别选取LSM定位算法、PSO定位算法、Gold-SA定位算法、改进后的Gold-SA定位算法进行仿真分析，仿真结果如图2所示。

图2a中采用LMS定位算法时，定位误差为2.5924m，由于室内环境复杂充满电磁干扰，导致精度低不能做到精确定位。由图2b和图2c看出,基于PSO的定位算法误差为5.9993cm，基于Gold-SA的定位算法误差为5.9866cm，虽然上述两种算法相比于LMS算法精度提高很多，但仍存在收敛速度慢的缺点。改进Gold-SA定位算法如图2d所示，定位算法误差为1.4703mm，相比PSO算法和未改进的Gold-SA算法，改进后Gold-SA算法的定位精度分别提升97.54%和95.52%。Levy变异机制增加算法搜索空间的多样性，自适应移动因子有效地避免群智能算法收敛早熟的缺点提高算法收敛速度，使算法误差明显减小，实现精确定位。在仿真参量不变的情况下对4个目标点进行同时定位，多目标仿真结果如图3所示。

Fig.3 Multi-target positioning error of the improved Gold-SA algorithm

由图3可以看出,采用改进Gold-SA算法对4个目标点同时定位，定位误差分别为1.170cm,1.243cm,1.197cm,1.470cm，平均定位误差为1.270cm。由图3仿真分析可知,改进后的Gold-SA定位算法可应用在多目标定位过程。

3.2 收敛速度仿真分析

分别对PSO算法、Gold-SA算法和改进后的Gold-SA算法进行单目标迭代速度的分析，设置迭代数为200次，初始种群数量为20，采用3×3网格型LED灯源排布方案，在保证使用最少LED灯源且定位精度较高的前提下分析算法收敛速度，仿真结果如图4所示。

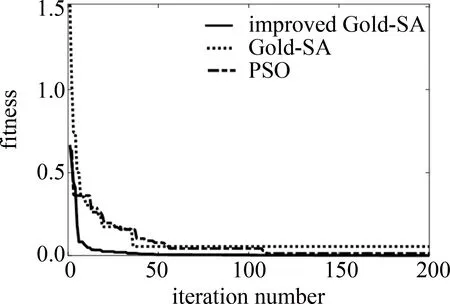
Fig.4 Convergence speed comparison chart

由图4可直观看出：采用Levy飞行变异机制结合自适应移动因子改进的Gold-SA算法收敛速度大幅度提升。改进后的Gold-SA算法经过40次迭代后就快速收敛到最低适应度值。基于PSO的RSSI定位算法110次迭代后收敛到最低适应度值，Gold-SA算法经过200次迭代后还未达到最低适应度值。因此，说明改进后的算法在快速定位方面更具有优势。

3.3 定位时间分析

选取改进Gold-SA算法、未改进的Gold-SA算法及PSO算法，在定位误差为0cm～2cm区间内仿真分析3种定位算法单目标定位时间，结果如图5所示。

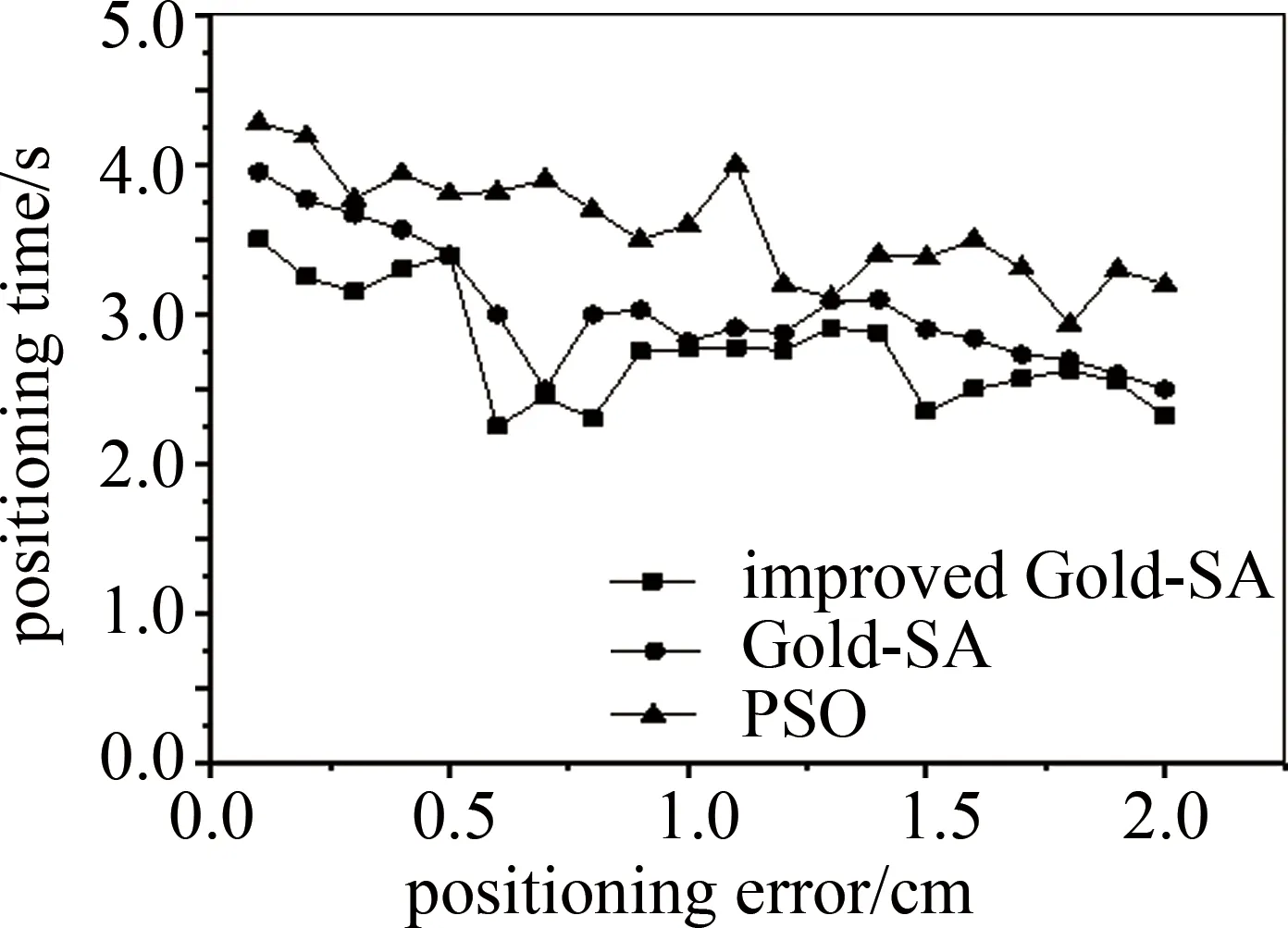
Fig.5 Comparison and analysis of positioning time

由图5中明显看出：3种算法在相同定位区间内，改进后的算法定位误差在0cm～2cm的范围内定位时间均比未改进的Gold-SA算法和PSO算法短，由此说明改进的Gold-SA算法可实现快速定位。当定位误差为0.2cm时，改进的Gold-SA定位时间为3.3s比传统Gold-SA算法快0.5s，比PSO算法快0.9s；定位误差为0.6cm时，改进后的算法定位时间为2.2s比传统Gold-SA快0.8s，比PSO算法快1.6s；定位误差为1.5cm时，改进后的算法定位时间为2.4s比传统Gold-SA算法快0.6s，比PSO算法快1s。由此可以说明改进后的Gold-SA算法相比于其它两种算法所需要的定位时间更短，改进后的Gold-SA算法整体优于未改进的Gold-SA算法和PSO算法。

3.4 平均定位误差分析

为进一步验证改进后的黄金正弦算法优越性，分别对改进的Gold-SA算法、Gold-SA算法和PSO算法分别进行200次单目标定位误差计算。采用直方图更直观地观测定位算法的误差分布，如图6所示。

Fig.6 Positioning error histogram

由图6可看出：与Gold-SA算法和PSO算法相比，改进后的Gold-SA算法误差大多集中在0cm～2cm范围内，当误差大于2cm时,误差点个数呈大幅下降趋势，在6cm～8cm范围内没有误差点分布。Gold-SA算法误差集中在2cm～4cm范围内，PSO算法误差主要分布在2cm～4cm,4cm～6cm范围内。改进后的Gold-SA算法相较与Gold-SA算法和PSO算法定位性能分别提高64.3%和68.9%。因此，改进后的算法相比于其它两种算法定位误差更小、定位效果更好。本文中对改进Gold-SA算法进行80次的误差计算，依然采用在10m×10m×3m的室内空间中3×3网格型LED灯源排布方案，误差折线图如图7所示。

Fig.7 Error line chart of the improved algorithm

图7中对改进的Gold-SA算法对单目标进行80次误差计算，经过多次仿真可以得出改进后的算法误差稳定在0cm～1cm区间内，最小误差可达1.4703mm。

由以上仿真综合分析可知，相比于PSO算法、Gold-SA算法和LMS算法，改进的Gold-SA算法具有收敛速度快、误差小趋于稳定等优点，改进后的Gold-SA算法相比PSO算法和Gold-SA算法定位性能更具优越性，满足室内高精度快速定位要求。

4 结 论

提出了一种基于黄金正弦算法融合自适应Levy飞行变异机制的室内可见光定位方法。在保证光强平坦性且不影响照明效果的前提下，采用3×3网格型LED灯源排布方案，设计RSSI结合改进Gold-SA算法实现室内精确定位。在传统黄金正弦的基础上引入变异机制和自适应移动因子后大大提高搜索空间的多样性，改善算法存在的收敛速度慢、易陷入局部最优等缺陷。在10m×10m×3m的室内空间中经过多次仿真：改进的Gold-SA算法定位误差最小可达1.4703mm，平均误差1cm左右。算法在迭代40次～80次之间可收敛到最低适应度值。本文中提出的改进黄金正弦定位算法具有定位精度高、定位速度快等优点，且能够实现多目标同时定位。因此，本文中的定位方法更适合大型室内场所精确、快速定位。