一道条件最值问题的多视角探究

广东省韶关市翁源县龙仙中学 (512600) 何琼英

二元条件最值问题是各类考试中的热点问题，这类问题形式新颖，题型灵活多变，难度比较大，技巧性强，以下来看一道这样的题目.

1.试题呈现

2.试题评价

这是一道二元条件下求一个分式型式子的最值问题，已知条件式可以化成圆的标准方程.本题出现在选择题第12题压轴题的位置，具有很好的区分度，较好的考查了考生分析问题和解决问题的能力，同时考查了方程思想、数形结合思想、化归与转化思想及其反映出的数学运算能力和逻辑推理能力.

3.多解探究

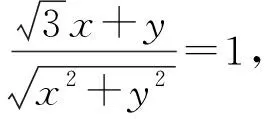
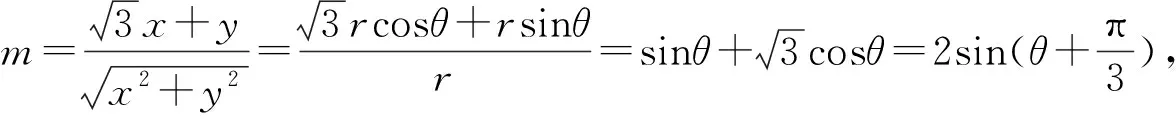
解后反思：利用三角换元法将要求的式子利用辅助角公式化为形如Asin(ωx+φ)的三角函数，将x和y三角换元后代入已知方程后分离出sinθ，利用基本不等式求出sinθ的最小值，求出θ的取值范围，利用三角函数的单调性可以求出最大值.

解后反思：运用圆的参数方程进行三角换元，把要求最大值的式子化为关于α的三角分式型函数g(α)，再求导函数，求出导函数的零点，讨论函数g(α)的单调性，从而求出g(α)在闭区间[0,2π]上的最大值.

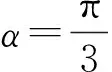
解后反思：先确定直线OM的倾斜角的取值范围，再由待求式的结构特征，联想到三角函数定义，再运用辅助角公式化简，把问题转化成求形如Acos(ωx+φ)的三角函数在给定闭区间上的最大值问题.

解后反思：由待求式的结构特征联想到向量的数量积公式，再数形结合，可求出∠MON的最小值，从而求出cos∠MON的最大值，进而得出待求式的最大值.

解后反思：将待求式加绝对值后，进行变形，由式子结构特征联想到点到直线距离公式和两点间距离公式，可以借助解析几何知识求解.

4.解题启示

上述几种解法，由待求式子的结构特征出发，运用齐次化法、三角换元法、平面向量的数量积和距离公式等方法和知识进行一题多解，这些不同解法都源于高中数学核心概念和核心方法，体现了运用的知识的基础性和方法的创新性，可以促进学生深层次理解高中数学基本概念和基本公式，提升学生的解题能力，开阔学生的解题视野，优化解题思路，提升学生的数学学科核心素养，落实运算求解、逻辑思维和创新能力等关键能力的培养.