一“点”牵想象 全面引运动——《图形的运动》总复习教学

文|金 奎

【教学内容】

人教版六年级下册第92、93页。

【教学过程】

一、给一点，自由想象

1.提出问题。

师：同学们，这节课我们来复习图形的运动。回忆一下，小学阶段我们学过的图形运动有哪些？

生：有平移、旋转、轴对称、放大与缩小。

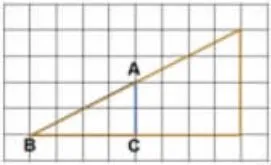
师：让我们张开想象的翅膀，一起进入图形运动的世界。请看：有这样一个三角形ABC，假如这个点是三角形ABC运动后其中的某个顶点的新位置。你知道它可能是怎么运动的吗？

【设计意图：先让学生回忆图形运动的多种方式，不断唤醒旧知；再通过创设“给出运动后某个顶点的新位置，研究可能是怎么运动的”这个问题，给了学生自由想象的思维空间。】

2.分层反馈。

（1）反馈。

层次一：平移。

师：通过分类，来说说这两幅图是怎么平移得到的？

生1：第一幅是把三角形ABC向右平移4格后得到的。

生2：第二幅则是把三角形ABC向右平移8格得到的。

师：因为平移的距离不一样，所以最后的位置也不一样。在描述平移的时候说清楚方向和距离很重要。

层次二：旋转。

师：这幅图是怎么得到的？

生：把三角形ABC绕点C逆时针旋转180度后得到，也可以把三角形ABC绕点C顺时针旋转180度后得到。

小结：旋转时，要说清楚绕点、旋转方向、旋转角度，缺一不可。

层次三：轴对称。

师：同样是轴对称图形，为什么第一幅这个点是点B的对应点，而第二幅是点C的对应点？

生：第一幅对称轴在AC的位置，第二幅对称轴则是在AC往右两格的位置。

师：轴对称的特点是对称点到对称轴的距离相等，并且连线与对称轴垂直。

层次四：放大与缩小。

师：下图又是怎么运动的？

生：三角形ABC按2∶1放大后的图形。

师：底放大到原来两倍的同时，高也相应地放大到原来的两倍，缩小也是同样的道理。

（2）概括。

师：刚才我们通过三角形ABC回顾了图形的运动。那么它们之间有什么相同点和不同点呢？

生1：无论是哪一种运动，运动前后图形的形状都没有发生改变。

生2：刚才画这些图形的时候我们都是按照先找点、再描点、最后连线的方法，所以画法也相同。

生3：不同点是：经过平移、旋转、轴对称，图形的大小不变，只改变了位置；而经过放大与缩小后，图形的大小改变了。

板书：

?

【设计意图：大多学生会把这一点想象成B点或C点的新位置，这样正好可以牵出各种运动的方式，在追问中及时复习运动的特点及要素。为了把这些分支加以整合，引导学生充分观察、对比运动方式，概括出不同点与相同点，真正体现出总复习课“联”“融”的意味。】

二、求变式，延伸想象

1.A到目标位。

师：在刚才的创造中，我们是把点B或点C运动到这一点，现在请你再次想象：能不能让点A运动到这点？

生1：先把三角形ABC向右平移4格，再向下平移2格。

生2：先把三角形ABC绕点C顺时针旋转90度，再向右平移2格。

生3：先把三角形ABC绕点A顺时针旋转90度，再向右平移4格，最后向下平移2格。

2.以AB为对称轴。

师：跳出这一点来继续想象，假如三角形ABC是轴对称图形的其中一半，以AB边为对称轴，你能找到点C的对称点吗？

生：我们可以利用轴对称特点找到点C的对称点。

3.以整体为一个图形。

师：如果以D点为绕点，把三角形ABC逆时针旋转90度，哪一幅图是正确的呢？

生：我们可以把这个点和点C连起来，整个图形看作小旗比较方便，所以第二幅是正确的。

师：把看不见的图形想象成了看得见的图形，想象的确能帮助我们更好地学习数学。

【设计意图：一“点”的价值不仅仅是运动特点的再现，更是有限的素材无限地使用。为了引发学生深层次的思维，教师引导学生“这一点如果是A点运动后的新位置，又可以怎么运动？”进行质疑，这样就可以从运动组合的角度加以理解；斜的对称轴课本只作介绍，为了体现总复习课适当提升的要求，通过改变对称轴的位置进一步拓展课本知识；通过D点为绕点，跳出原有“点的位置”的研究框架，转入整个图形的运动。此时的选择已是“无线”化“有线”，并再一次突破像小旗这类看上去简单、实则无载体依靠的难点。】

三、创练习，丰富想象

1.选择题。

（1）下面（ ）张扑克牌，旋转180°后看到的与原来相同。

2.填空题。

①△ABC绕点C顺时针旋转150°，点B正好落在长方形CDEF的DE边上，那么∠1= °

②下图中，右边三角形是左边三角形沿着对称轴画出的轴对称图形。根据图中信息，点A的位置用数对表示是（ ）。

A.（6，10） B.（10，6）

C.（6，11） D.（11，6）

3.面积计算。