信赖域子问题求解方法及其数值试验研究

袁 远

（滁州城市职业学院教育学院，安徽滁州 239000）

信赖域算法是目前求解无约束优化问题的一类常用的数值计算方法，在宏微观经济分析、交通运输管理、能源通信工程、机械结构设计等众多领域应用广泛。信赖域子问题是信赖域算法的重要组成部分，子问题的不同求解方法直接影响着信赖域算法的数值计算效率〔1〕。目前，求解信赖域子问题的方法主要有〔2〕：1）精确求解方法。目前的精确求解方法主要是牛顿法，然而一般意义上，精确求解方法在计算时需要相当的工作量。例如，李亮等〔3〕利用分段性插值的方法提出了一种新的精确求解方法，称为分段折线法。2）折线法。折线法就是利用一条折线来近似这条最优曲线，然后得到子问题的近似解。例如，赵英良等〔4〕的切线单折线法等。3）共轭梯度法。共轭梯度法不需要计算和存储，是解决大型问题的首选方法。例如，赵英良等〔5〕提出的共轭梯度法解信赖域子问题的重新开始策略等。传统的信赖域算法为了保证算法的整体收敛性，采取的都是具有单调下降性质的算法，即在算法中要求Predk=q（k）（0）－q（k）（sk）＞0 以及成功迭代步满足γk≥η1＞0〔6〕。但在解决实际问题中，当目标函数的非线性性态较强时，如著名的Rosenbrock 函数（曲率变化剧烈），严格单调下降的算法出现了负面影响，步长很小，收敛速度十分缓慢〔7〕。因此，不同算法的适应性与优劣程度不一致。本文主要从信赖域子问题的角度，讨论和阐述几种无约束优化的信赖域算法，并且通过数值试验来探究这些算法在求解信赖域子问题时的优劣程度。

1 信赖域子问题与算法概述

1.1 非线性优化的信赖域算法对于无约束优化问题

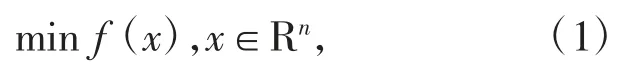
对于无约束优化问题（1），利用二次逼近，得信赖域算法的模型子问题：

其中s=x-xk，gk=f（xk），Bk是一个对称矩阵，它是Hessian 矩阵△2f（xk）或其近似，△k＞0 为信赖域半径，||·||为某一范数，通常采用l2范数。

根据模型函数q（k）（s）与目标函数f（x）的一致性程度来调整信赖域半径△k。对于式（2）的解sk，设目标函数f（x）在第k 步的下降量

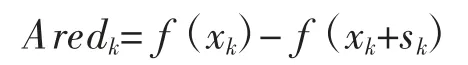
为实际下降量，设模型函数q（k）（s）在第k 步的下降量

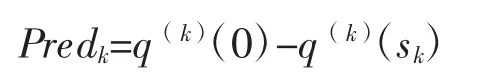
为预测下降量。定义比值

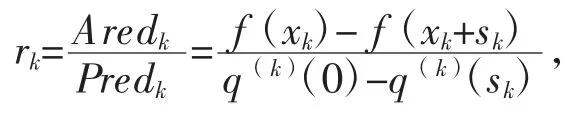
它衡量了模型函数q（k）（s）对目标函数f（x）的拟合程度。如果rk越接近1，说明模型函数q（k）（s）对目标函数f（x）的拟合估计效果越好，这时可以增大△k以扩大信赖域；如果rk＞0 但不接近1，保持信赖域半径△k不变；如果rk接近0 或取负值，说明模型函数q（k）（s）对目标函数f（x）的拟合效果很差，则应该减小△k，缩小信赖域。

1.2 求解信赖域子问题的算法信赖域算法实现的关键在于信赖域子问题（2）的有效求解，本文分别阐述求解信赖域子问题的3 种近似求解方法：不定折线法、Moré-Sorensen 法、截断共轭梯度法。

（1）不定折线法

对于信赖域子问题（2），当||Bk-1gk||＞△k时，折线法可以较为轻松地找到子问题（2）的近似解。在矩阵Bk不正定的情况下，朱红兰等〔6〕提出了一种不定折线法，不定折线法的基本思想：

①若Bk是正定的，则Γ（k）是Powell 的单折线路径：Γps（k）＝［xk，xkcp，xknp］，其中xkcp，xknp分别为柯西点和牛顿点；

②若Bk是不正定的，有4 条路径Γ（k）可选择：

（i）当gkTBkgk＞0 时，若gkTL-Tv≥0 或者当gkTL-Tv＜0 且，选择路径：Γs1（k）＝［xk，xkcp，g］；

（ii）当gkTBkgk＞0 时，令skB=-（Bk+μI）-1gk，xkB＝xk+skB，若||skB||≥△k且||skB||2＞（skB）Tskcp＞||skcp||2，选择路径：Γs2（k）＝［xk，xkcp，xkB］；

（iii）当gkTBkgk＞0 时，除了（i）和（ii）两种情况外：Γs3（k）＝［xk，xkB，ŝ］，ŝ=sgn（sTskB）s；

（iv）当gkTBkgk≤0 时，若，选择路径：Γs4（k）＝［xk，xkB，-gk］；否则选择路径：Γs3（k）＝［xk，xkB，ŝ］。

（2）Moré-Sorensen 法

当μk充分大时，（Bk+μkI） 是正定的，Moré-Sorensen 法〔2〕将子问题（2）的求解基本上归结于求下述方程组

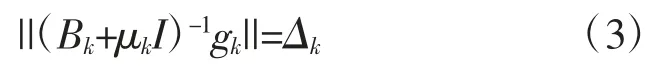
的解。令p（μk）=-（Bk+μkI）-1gk，（3）式即为

将矩阵Bk进行特征分解以便研究||p（μk）||的一些性质。因为Bk是对称矩阵，所以存在一个正交矩阵Q 以及一个对角矩阵Λ=diag（λ1，λ2，…，λn）（其中λ1≤λ2≤…≤λn且都是Bk的特征值），使得Bk=QΛQT，则Bk+μkI=Q（Λ+μkI）QT。当μk≠λj时，有

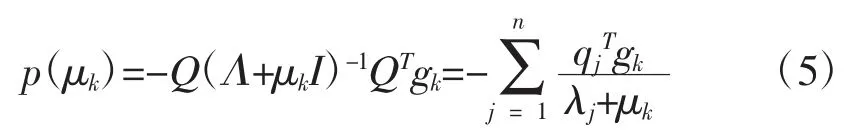
成立。式中qj为矩阵Q 的第j 列向量，所以进一步有

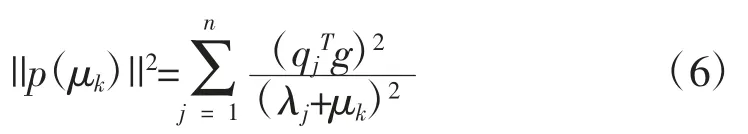
成立。事实上，如果μk＞－λ1时，则对于所有的j＝1，2，…，n，μk+λj＞0，由（6）式可以得到此外，如果qjTgk≠0，则有。所以，根据以上两个性质，可得p（μk）在μk∈（-λ1，+∞）是一个连续、单调递减的凸函数，所以方程||p（μk）||＝△k在μk∈（-λ1，+∞）有唯一解μk*。令

当μk略大于－λ1时，方程φ（μk）＝0 的解可以用牛顿迭代法来近似求得，设其解为μk*，将此代入p（μk）中，即可求出子问题（2）的解。

（3）截断共轭梯度法

考虑与问题（2）相对应的线性方程组

Steihaug〔7〕指出，当矩阵Bk正定时，运算精确的共轭梯度法至多经过n 次迭代可求得方程组（7）的最优解－Bk-1gk。

（i） 若dkTBkdk≥0，dk＝－△f（xk）且||Bk-1gk||≤△k，则sk＝－Bk-1gk。

（ii）当||sk||≤△k，||sk+1||≥△k，此时不论矩阵Bk是否正定，都能够确定≥0 使得sk+1＝sk+ dk满足||sk+1||=△k，取sk+1作为问题（2）的近似解。

（iii）若dkTBkdk≤0，即矩阵Bk不正定时，dk为矩阵Bk的一个负曲率方向，这时sk+1＝sk+ dk，使得||sk+1||=△k，取sk+1作为问题（2）的近似解。

2 数值结果与分析

2.1 对于中小规模问题的数值试验采用Matlab R2012b 软件，通过求解3 个试验函数的无约束最优化问题，从而对不定折线法、Moré-Sorensen 法、截断共轭梯度法3 种算法的数值计算效率进行比较。本文从国际上较流行的测试问题软件包〔8〕和文献〔9〕中选取了21 个试验函数来进行数值试验，试验函数名称和规模（n 的大小）见表1。本文以求解无约束极小化问题的函数值迭代次数的大小为评价数值计算效率的指标。

表1 试验函数名称

比较不定折线法、Moré-Sorensen 法、截断共轭梯度法3 种算法在单调、非单调情况下（通过选取不同的非单调控制参数M 值实现改变算法的单调性数值效率，M=0 时数值效率最差呈单调性，M=10时数值效率较好呈非单调性〔10〕）求解中小规模问题的数值计算效率。表2 为在单调情况下所测试的3种算法的数值结果，表3 为在非单调情况下所测试的3 种算法的数值结果。其中ng 表示梯度迭代次数，nf 表示函数值迭代次数，min f 表示函数的最优值。

表2 M＝0 单调时的数值结果

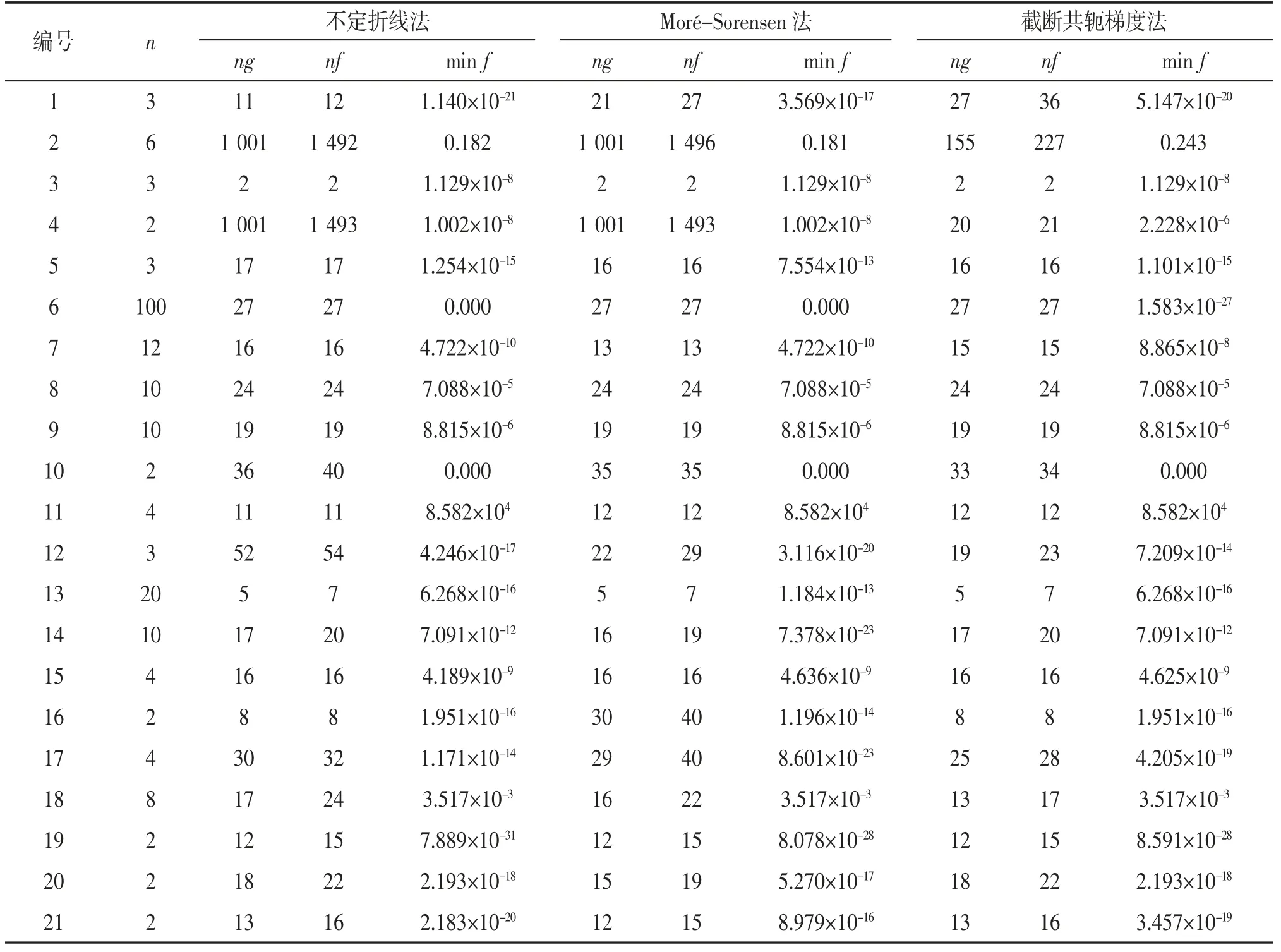
表3 M＝10 非单调时的数值结果

续表2

从表2 可以看出，当M＝0 时，不定折线法、Moré-Sorensen 法、截断共轭梯度法在求解第3、6、13、15、20 问题时计算效率一致，而截断共轭梯度法在解决问题2、4、5、12、17、18 时数值计算效率明显高于其他两种算法，Moré-Sorensen 法在解决问题1、7、8、9、19 时效率最好，而不定折线法只在解决问题11、14、21 时效率较好。从表3 可以看出，当M＝10 时，不定折线法、Moré-Sorensen 法、截断共轭梯度法在求解第3、6、8、9、13、15、19 问题时计算效率一致，而截断共轭梯度法在解决问题2、4、10、12、17、18 时数值计算效率明显高于其他两种算法，Moré-Sorensen 法在解决问题7、14、20、21 时效率最好，而不定折线法只在解决问题1、11、16 时效率较好。综上所述可以得出在单调、非单调情况下，截断共轭梯度法在求解以上无约束优化问题上的数值计算效率略好于Moré-Sorensen 法，明显优于不定折线法。

2.2 对于大规模问题的数值试验当某些试验函数维数n 很大，即处理一些大规模问题时，不定折线法、Moré-Sorensen 法、截断共轭梯度法3 种算法在单调、非单调情况下的数值计算效率是不同的。探究和比较这3 种算法在非单调情况下（M=5）解决大规模无约束极小化问题的数值计算效率。本文所用到的试验函数名称及维数见表4，其中n 分别取100、500 和1 000。

表4 大规模测试问题

在Matlab R2012b 软件中编制程序求解上述7个试验问题，得到以下数值试验结果。表5~7 分别表示在n=100、n=500 和n=1 000 时3 种算法的数值结果。

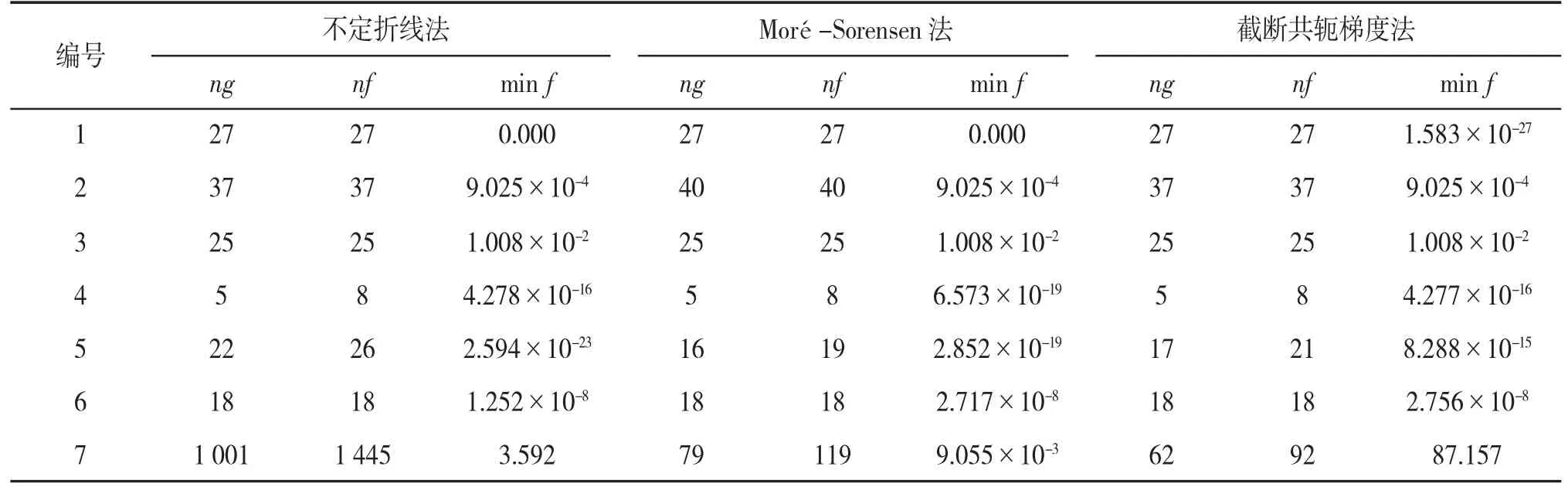
表5 n=100 的数值结果

从表5 可以看出，当n＝100 时，不定折线法、Moré-Sorensen 法、截断共轭梯度法3 种算法除了在解决第1、3、4、6 问题上计算效率一致，截断共轭梯度法还在解决问题7 时数值计算效率高于其他两种算法，Moré-Sorensen 法在解决问题5 时高于其他两种算法，而不定折线法只在解决问题2 时效率较好。从表6 可以看出，当n＝500 时，不定折线法、Moré-Sorensen 法、截断共轭梯度法3 种算法除了在解决第2、6 问题上计算效率一致，截断共轭梯度法还在解决问题7 时数值计算效率高于其他两种算法，Moré-Sorensen 法在解决问题4 时高于其他两种算法，而不定折线法只在解决问题5 时效率较好。从表7 可以看出，当n＝1 000 时，不定折线法由于求解时间过长，软件并未算出最终结果，可见当函数维数较高时，其数值计算效率最低。而截断共轭梯度法在解决第2、5 问题上计算效率要高于Moré-Sorensen 法。综合以上分析可以得到：截断共轭梯度法在解决大规模问题时，它的数值计算效率高于不定折线法和Moré-Sorensen 法，并且可以发现当规模越大时，其数值计算效率越明显高于其他算法。

表6 n=500 的数值结果

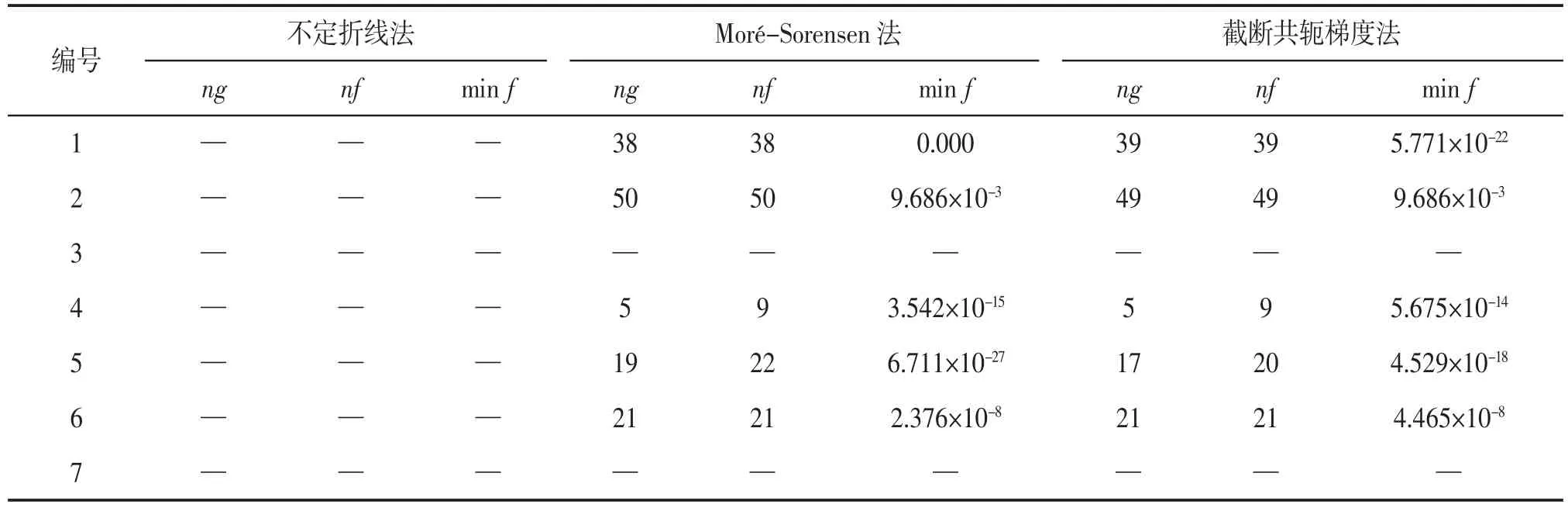
表7 n=1 000 的数值结果

2.3 对于病态问题的数值试验针对病态的无约束优化问题，运用不定折线法、Moré-Sorensen 法、截断共轭梯度法3 种算法分别在单调和非单调情况下进行求解。本文选取的病态问题是著名的Rosenbrock 函数

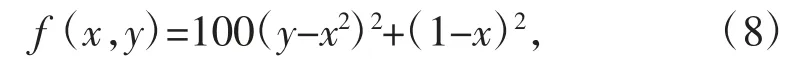
通过求解这个函数来比较单调、非单调的不同算法数值计算效率。利用Matlab R2012b 软件求解该无约束优化问题，得到的数值试验结果见表8。

同时记录求解函数时的一系列迭代点，其中初始迭代点为（-1.2，1.0），最优点为（1.0，1.0）。用Matlab R2012b 将这些迭代点描出并反映在Rosenbrock 函数的等值线图上，便可清晰直观地比较单调算法和非单调算法的迭代路径和计算效率，结果见图1~3。

对比分析图1（a）和图1（b），非单调的不定折线法求解的迭代次数小于单调的不定折线法，而且在图1（a）中当迭代点接近最优点时，收敛速度变得非常慢，相反在图1（b）中当迭代点接近最优点时，收敛速度加快。对比分析图2（a）和图2（b），非单调的Moré-Sorensen 法求解的迭代次数明显小于单调的Moré-Sorensen 法，而且在图2（a）中当迭代点接近最优点时，收敛速度变得非常慢，相反在图2（b）中当迭代点接近最优点时，迭代路径明显有变化，收敛速度明显加快。对比分析图3（a）和图3（b），非单调的截断共轭梯度法求解的迭代次数明显小于单调的截断共轭梯度法，而且在图3（a）中当迭代点接近最优点时，收敛速度变得非常慢，相反在图3（b）中当迭代点接近最优点时，收敛速度明显加快。因此，当处理的函数出现峡谷形时，相比于单调的信赖域算法，非单调的算法在最优点附近的收敛速度要快得多，数值计算效率更高，而且这种算法的数值计算是相对比较稳定的。

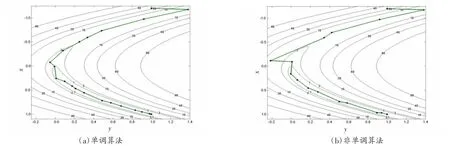
图1 不定折线法求解的迭代点图

图2 Moré-Sorensen 法求解的迭代点图

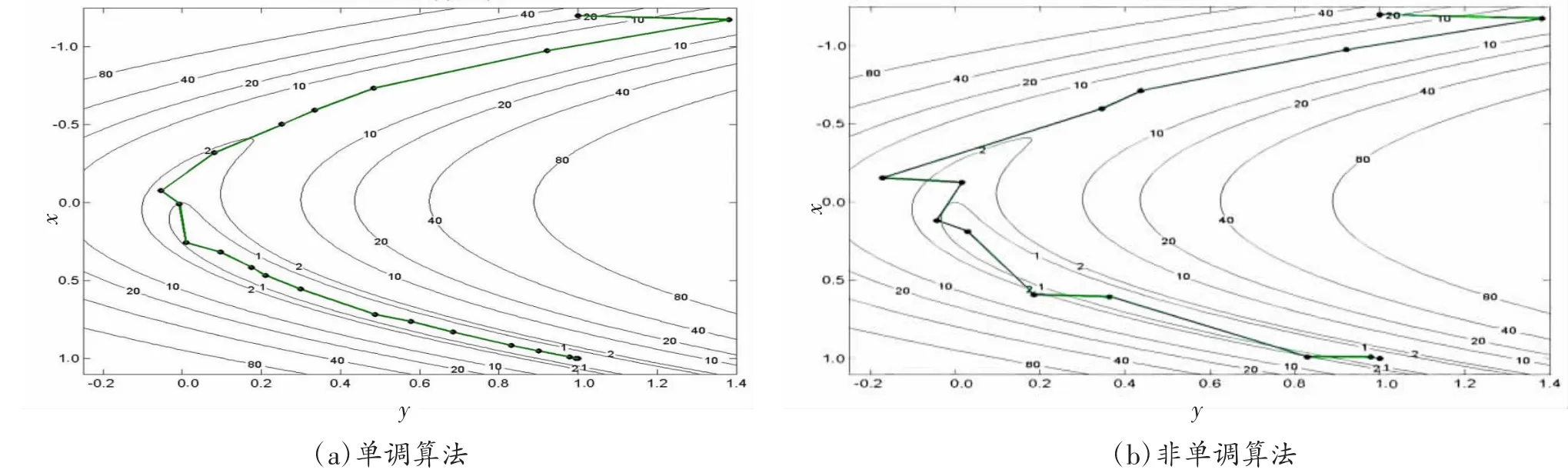
图3 截断共轭梯度法求解的迭代点图

3 结论

本文主要比较了解决信赖域子问题的几种算法的数值计算效率，通过大量的数值计算得出截断共轭梯度法在一定程度上计算效率优于Moré-Sorensen 法以及不定折线法，而且在解决大规模问题时，其计算效率更是明显高于其他两种算法。此外在解决一些病态问题上（如Rosenbrock 函数），非单调的信赖域算法收敛性更强、数值计算效率更高。然而，本文所用到的测试函数还十分有限，若想更全面地评估各种信赖域子问题求解方法的数值计算效率，还须做进一步的探究。