基于贴进度的模糊决策表属性约简启发式算法

罗秋瑾

（云南财经大学统计与数学学院，昆明 650221）

波兰科学院院士Pawlak〔1〕教授于1982 年提出的粗糙集理论是处理知识中不完整、不确定性问题的强有力工具，经过几十年的发展，经典的粗糙集模型不断渗透到其他相关领域，近年来其广泛应用于医学、金融、专家系统、知识发现、机器学习、数据挖掘、决策分析等多个领域中〔2〕，并且取得了很好的效果，得到了广泛的关注。

法国学者Dubois 和Prade〔3〕提出的模糊粗糙集就是为了解决粗糙集离散化过程的信息损失问题。模糊粗糙集将粗糙集和模糊集集成在一起，是粗糙集的扩展，它能同时处理数据中的模糊性和粗糙性〔4-5〕。所以，有理由相信在处理复杂环境中的不确定性时，模糊粗糙集比粗糙集和模糊集更有效。给定一个模糊信息系统，每个模糊条件属性对决策分类的贡献不尽相同，有的贡献非常大，有的贡献比较小，甚至没有贡献。这意味着需要找出对分类起主要作用的条件属性，删除其中没有贡献的条件属性，用以提高运算效率，此过程称为属性约简〔6〕。

目前几乎所有的关于基于模糊粗糙集的属性约简的研究都是从文献〔7〕开始的，但是由于这种方法完全是从形式上把经典粗糙集中相应的方法甚至符号照搬过来，对基于模糊粗糙集的属性约简的本质没有清楚的认识，因而导致设计的属性约简算法不收敛。对此，Cheng 等〔8〕通过模糊粗糙集的粒结构引入辨识矩阵的方法来计算属性约简，但是通过实例发现，某些情况下求出核属性后条件属性却无法进行有效约简。

本文提出一种新的约简算法，首先利用贴进度生成可辨识矩阵，再由可辨识矩阵得到一种改进的计算相对核属性的算法，再基于核属性生成最小约简的启发式算法，最后用实例说明此方法的有效性。

1 基本概念

定义1 设U 是一个对象集合，A 是一个非空实数值属性集合，称（U，A）是一个模糊信息系统。如果把A 中的属性分成条件属性和决策属性，则称模糊信息系统为模糊决策系统〔9〕。

贴进度用来刻画两个模糊集的接近程度〔9〕。

定义2 设映射N：F（X）×F（X）→［0，1］满足以下条件：

（1）∀A∈F（X），N（A，A）＝1；

（2）∀A，B∈F（X），N（A，B）＝N（B，A）；

（3）若∀A，B，C∈F（X），∀x∈X 满足：｜A（x）-C（x）｜≥｜A（x）-B（x）｜，则有N（A，C）≤N（A，B），则称映射N 为F（X）上的贴进度，称N（A，B）为A 与B的贴进度。

定义3 设映射N：F（X）×F（X）→［0，1］，∀A，B∈F（X），当X=｛x1，x2，…，xn｝时，令

可以验证此定义的N（A，B）满足贴进度定义的3 个条件〔10〕。

利用贴进度定义两个模糊集的模糊相似关系〔11〕。

定义4 设R 是论域U 上的模糊关系，已知U上的n 个模糊集Ai，i=1，2，…，n，∀x，y∈U，定义R（x，y）＝N（A，B）。

定义5 设（U，R）是模糊信息系统，X⊆U 是经典集合，称R（X）是X 关于（U，R）的模糊下近似，其隶属函数定义为〔11〕：

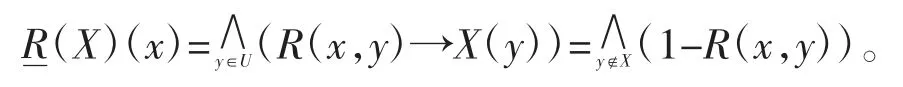
定义6 设U=｛x1，x2，…，xn｝，MD（U，R）是一个n×n 矩阵（cij），称为（U，R∪D）的可辨识矩阵〔12〕，定义为：

（1）（cij）=｛R：1-R（xi，xj）≥λi｝，λi=Sim（R）（［xi］D）（xi），λj＝Sim（R）（［xi］D）（xj），如果λi>λj；

（2）（cij）=Ø，其他。

其中Sim（R）（xi，xj）=∧（1-∨i≠j｜xi-xj｜）。

2 基于贴进度的属性约简

基于模糊粗糙集的属性约简的基本思想就是保持决策类相对于条件属性的正域不变的前提条件下，删除其中不必要或不重要的条件属性。人们往往期望找到具有最少条件属性的约简方法，即最小约简。然而遗憾的是，已经有学者证明了找出一个决策表的最小约简是NP-hard 问题。导致NPhard 问题的主要原因是属性的组合爆炸问题。在很多属性约简算法中，一般都要求先求出核属性集，然后再由核属性通过启发式知识扩展到最小约简。因此，求核成了属性约简求解的关键步骤。

2.1 对原算法的一些分析Cheng 等〔8〕通过模糊粗糙集的粒结构引入辨识矩阵的方法，提出计算相对核的方法，CoreD（R）＝｛R：cij=｛R｝｝，i≥1，j≤n，从而得到约简属性集为RedD（R）=∪RoreD（R）。但此方法是由经典粗糙集照搬到模糊粗糙集，导致方法存在一定的问题。比如通过实例计算，发现此方法在某些时候无法对条件属性集进行约简，即此时RedD（R）=R。所以这时候仅仅根据相对核属性得到约简属性集的算法就失效了，需要对原方法进行改进。

2.2 改进算法针对以上问题，本文重新定义了基于可辨识矩阵的条件属性的相对重要度，不仅要考虑矩阵中仅出现的单个属性，而且还要兼顾该属性出现的总的频率数，由相对重要度计算出相对核属性后再进而求出相对条件属性约简，再计算约简条件属性和决策属性的贴进度，大于预先设定的某个阈值λ 时，则输出该约简。

定义7 设有模糊决策表（U，A，d），属性ai∈A相对于决策属性d 的相对重要性，其中｜ai｜表示在MD（U，R）中cij=ai的频率数，｜∪ai｜表示cij中所有包含ai项的频率数。

基于贴进度的模糊决策表属性约简算法：

输入：模糊决策表（U，A，D），其中A＝｛a1，a2，…，an｝。

输出：A 的约简Red。

（1）计算基于贴进度的可辨识矩阵MD（U，R）；

（2）计算MD（U，R）中γ（ai），取γ（ai）中最大值，令Red=｛ai｝；

（3）将MD（U，R）中含Red 的项全部置为Ø，再计算γ（ai，aj），其中aj∈A-Red，取γ（ai，aj）中最大值，令Red=｛ai，aj｝；

（4）计算N（Red，d），如果N（Red，d）≥λ，则输出约简Red，否则转到步骤（3）。

3 实例说明

表1 是一个模糊决策表，该决策表的论域U=｛x1，x2，…，x6｝，条件属性集A=｛a1，a2，a3｝和决策属性｛d｝。

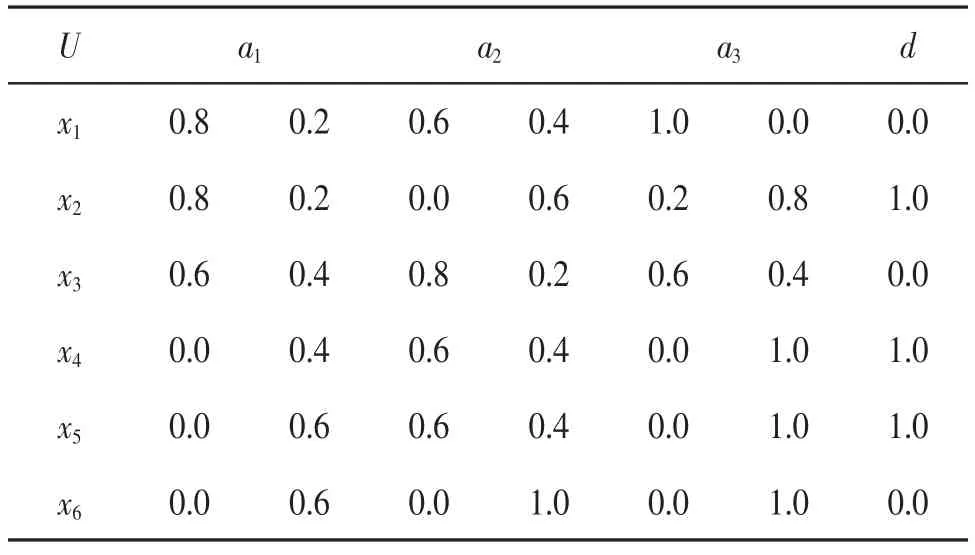
表1 模糊决策表

由决策属性d 得到两个划分分别为：X1=｛x1，x3，x6｝，X2=｛x2，x4，x5｝，则

从而计算出相对核属性为｛a2｝，再将含a2的项置为Ø，从而得到

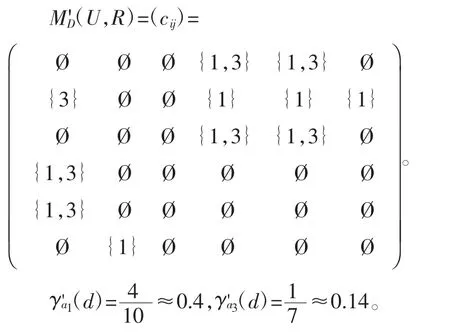
得到相对约简｛a1，a2｝，此时属性｛a1，a2｝对于决策属性集d 的贴进度为0.84>0.8，输出约简｛a1，a2｝。

4 结论

本文引入贴进度提出一种改进的可辨识矩阵的生成算法，进而提出一种新的模糊决策表的属性约简算法，将原算法约简不了的情况进行改进，实验表明，该算法能降低一定的时间复杂度，并能处理规模较大的决策表。但模糊决策表类型较为复杂，此算法仅对其中的一种有效，在后续的研究中将逐步解决其他类型的决策表的属性约简问题。