基于OBE 理念的“离散数学”课程教学研究

张 勇

（巢湖学院信息工程学院，安徽巢湖 238024）

OBE（outcomes-based education）〔1〕在20 世纪80 年代由William Spady 提出，他强调教育中要关注学生的学而不是教师的教，作者在其著作Outcome-Based Education：Critical Issues and Answers中对OBE 的内涵和模型进行了深入和细致的阐述，解释了“什么是OBE”“为什么需要OBE”“如何实施OBE”这些关键问题。OBE 已被美国工程与技术认证委员会（ABET）全面接受，在美国、英国等西方国家广泛应用于教学改革。OBE 作为一种新的教育理念，它通过课程设计和实施来保证学生各种能力的达成，因此需要将课程、教的方法、学的方法及学习评价结合起来以提高学生能力〔2〕。2013 年我国成为“华盛顿协议”签约成员，OBE 理念被我国越来越多的高校接受，并应用于工程教育改革〔3-4〕。OBE理念有3 个核心要素，一是学生中心，二是产出导向，三是持续改进。OBE 理念把全体学生学习效果作为关注的焦点，教学设计和实施目标是保证学生取得特定学习成果〔5-6〕，通过建立“评价—反馈—改进”这一闭环〔7〕，形成持续改进的机制，从而进一步提高人才培养质量。

以研究离散结构为典型特征的“离散数学”成为现代数学不可或缺的组成部分，它在以计算机为代表的工程类专业人才培养体系中处于重要地位〔8-10〕。一方面，计算机学科所需的计算思维能通过“离散数学”得到有效训练；另一方面，可以选择离散结构对客观世界中的问题进行建模，最终通过计算机求解；此外，“离散数学”为计算机学科中核心课程的学习提供有效支撑。当前本科高校开设的“离散数学”课程内容主要聚集4 个典型离散结构。见图1。

图1 离散结构

1 OBE 理念下的教学设计

围绕本课程在人才培养目标中的地位与作用，按照毕业要求实现矩阵，设计3 个课程目标，并且这3 个课程目标CO1、CO2、CO3 分别对应毕业要求3 个指标点1.2、2.1、2.2，使得每个离散结构的教学最终都能支撑毕业要求。见表1~3。

表1 课程目标

表2 课程目标对应毕业要求指标点的支撑

表3 课程内容对应课程目标

2 教学方法与课程评价

教与学中不仅强化理论，更注重实践，关注学生在学习中是否获得，对于课程目标能达成多少。理论环节，通过案例教学法、可视化技术分析，充分利用各种资源，让学生理解离散结构，将本学科、专业领域前沿知识和技术如人工智能、机器学习及时引入“离散数学”课程各模块的课堂教学，使得学生认识到“离散数学”课程与计算机前沿知识是紧密联系的，增强学生学习动力和兴趣，并加强与学生互动，启发学生思考。实践环节，设置课程教学内容时充分考虑知识点的算法化、可编程性，增强课程的实践性，促使该课程与程序设计课程无缝衔接，使得学生能够将相关离散问题用计算机编程解决。编程实验以作业形式由学生完成，教师进行指导；另一方面，引导学生运用离散数学知识解决具体应用问题，并参加相关学科竞赛或申报各类大学生创新项目。通过这一环节，使得学生能够使用离散知识对实际工程问题建立离散模型求解，激发学生发挥潜能，对所学知识进行融会贯通和拓展应用，培养创新性思维。此外，教学中充分利用以慕课（MOOC）为代表的优质教学资源，开展形式多样的教与学活动，建设多渠道师生互动平台。

对于课程评价，主要基于课堂表现、平时作业及考试三环节来实现，由于是首次教学改革，对于这三部分的权重比较保守，后期将采用更灵活的权重设计，降低考试权重，提高过程权重。见表4。

按照OBE 理念，考试试卷每一题内容均支撑一个课程目标，见表5，支撑同一课程目标的试题分值符合表4 中各课程目标考核成绩比例，通过这些试题的考核，最终可以计算各课程目标达成度情况。

表4 各课程目标考核成绩比例

表5 考试内容与各课程目标对应情况

课堂表现的评价，可以通过课堂上与学生的互动，包括抢答或指定学生回答，也可以通过MOOC，实施翻转课堂，对学生表现采取量化评价，尽可能培养学生学习热情，激发学习潜力。

对于课后作业的设计，注重形式多样，包括推理证明，非标准答案作业，离散问题的编程解决等多种形式，使得学生在掌握理论知识的同时，实践能力和创新能力得到提高。作业的提交和批改主要通过网络平台（如学习通），便于作业的保留和数据的统计分析。

3 教学效果及分析

通过计算达成度来评价每一个学生课程的学习效果，首先根据公式（1）~（3）计算出3 个课程目标达成度，再根据公式（4）计算出课程达成度。其中：D 表示课程目标的达成度；Di表示第i 个课程目标的达成度；Xi表示第i 个课程目标作业平均成绩/第i 个课程目标作业成绩目标值；Yi表示第i 个课程目标课堂表现成绩/第i 个课程目标课堂表现成绩目标值；Zi表示第i 个课程目标考试成绩/第i 个课程目标考试成绩目标值。

按这种计算方法，对某高校2020 级软件工程专业2 个班（共105 人）课程达成度进行了计算，图2 是CO1 达成度分布图，图3 是CO2 达成度分布图，图4 是CO3 达成度分布图。

图2 CO1 达成度分布图

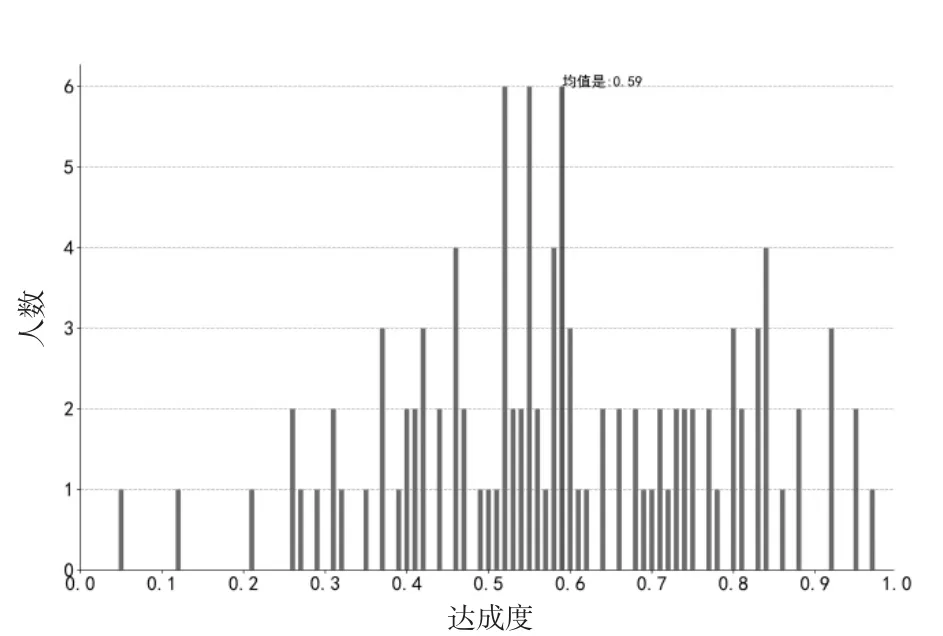
图3 CO2 达成度分布图

图4 CO3 达成度分布图

课程目标1 中达成度0.5~0.79 的46 人，0.8 及以上的37 人，说明学生能够针对软件工程领域具体的对象建立数学模型并求解。35.2%的同学能更好地达到该目标，但是9.5%的同学达成度低于0.4，说明这些同学与该目标还有距离。

课程目标2 中达成度0.5~0.79 的53 人，0.8 及以上的21 人，说明部分学生基本能够运用到识别和判断实际工程问题的关键环节，具备运用基本理论分析和解决实际问题的能力。20.0%的同学能更好地达到该目标，但是14.3%的同学达成度低于0.4，说明这些同学与该目标还有距离。

课程目标3 中达成度0.5~0.79 的46 人，0.8 及以上的38 人，说明学生能够运用具体与抽象相结合的方法表达软件工程领域中复杂的工程问题，具备运用图论和数学模型方法解决实际问题的能力。对于这一目标36.2%的同学能更好地达到，但是11.4%的同学达成度低于0.4，说明这些同学与该目标还有距离。

总体来看，3 个课程目标的达成度分别为0.68、0.59、0.68，反映学生基本达到每个课程目标，对于课程目标2 相对达成度较低，这反映出数理逻辑的理论存在一定难度，学生有畏难情绪，最终造成学生使用数理逻辑解决实际应用问题的能力较差，此外，也可以看出两极分化现象严重，说明部分学生学习态度不端正，积极性不高，并没有认真参与课程的学习，部分学生对于知识点的理解停留在表面，不能灵活运用，反映知识与能力的脱节。

将2020 级软件工程专业“离散数学”课程期末考试情况与2019 级相同专业作对比分析，两届试卷均由同一课程组命题，难易程度相近，由于2019级该专业未采用OBE 理念进行课程教学，对试卷平均成绩及试卷成绩各分数段这两个指标进行了对比，见图5~6，可以看出2020 级学生成绩显然优于2019 级，说明基于OBE 理念的教学设计在一定程度上效果优于传统教学设计，它能驱使各教学环节以学生为中心，对于传统教学中存在的问题有很好的靶向性。

图5 近2 年试卷平均成绩图

4 结束语

本文基于OBE 理念对“离散数学”课程进行了教学设计，通过毕业要求反向设计课程目标，并结合具体教学实践给出教学效果分析，对各目标达成度进行了分析，为相关课程的教学改革提供了一种有益思路。

图6 近2 年试卷各分数段人数