关于Smarandache函数的Möbius变换与欧拉函数
廖群英, 白海荣, 董 坤
(四川师范大学 数学科学学院, 四川 成都 610066)
1 引言及主要结果
1993年,Smarandache[1]首次定义了正整数n的Smarandache函数
S(n)=min{m:m∈N,n|m!}.

为叙述方便,设p、q、γ均为素数,τ(n)、ω(n)和p(n)分别为正整数n的正因子个数、不同的素因子个数和最小的素因子,ω(M)为集合M中所有元素的不同素因子个数,并记:
A1={2t,t≤6},
A2={24p(p=5,7),23p,22×52}∪
{22p,2p2(p=5,7),2p},
A3={22×5p(p=7,11,13),
2×7×11,2×5p},
B1={34×2,33×2t(t≤3),
32×2t(t≤4)}∪{3×2t(t≤6)},
B2={33×2×5,32×23×5,32×2p}∪
{32×22p(p=5,7,11,13),3×25×5}∪
{3×23p,3×24p(p=5,7),3×22×52}∪
{3×22p,3×2p2(p=5,7),3×2p},
B3={3×22×5p(p=7,11,13)}∪
{3×2×7×11,2×3×5p},
其中
ω(Ai)=i,ω(Bi)=i+1, 1≤i≤3.


1)n=p≥5;
2)n∈{3t(1≤t≤3),3p(p≥5),32×5};



定理 1.3设p≠q,n∉{1,p,pq}且p(n)≥5,则

2 相关引理
为后文叙述方便,记:
C1={1,3,5,7,9,11,13,15}∪
{21,27,33,35,39,45,63,105},
C2={1,3,5,7,9,11,15,21,27,33,45},
C3={1,3,5,7,9,15,21},
C4={1,3,5,9,15},C5={1,3}.
为证明本文的主要结果,需要如下几个引理.
引理 2.1[11]设n为正整数,则
特别地,若n为正奇数,则
引理 2.2设n为正整数,则
此时

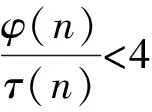
现设i≥1,直接计算可知:

D1={1,3},D2={5,9,15},
D3={7,21},D4={45,27},
D5={11,33},D6={13,35,39,63,105},



1)n=2m,m∈C1;
4)n=24m,m∈C4=D1∪D2;
5)n=25m,m∈C5=D1.
这就完成了引理2.2的证明.
引理 2.3设p为素数,n为正整数,且

则当p=3|n或p≥5时,有
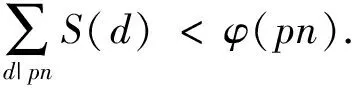
证明等价地,只需证明

事实上,易知

以及由题设条件及引理2.2知φ(n)≥4τ(n).进而,若n的标准分解式为n=p则α=0时,有
(p-1)φ(n);
而α≥1时,有
φ(pn)=(p-1)p
p(p-1)p
因此,当p=3|n时,有
φ(3n)-φ(n)=2φ(n),
从而

3τ(n)=(φ(n)-τ(n))-2τ(n)>0.
当p≥5时,有
φ(pn)-φ(n)≥(p-2)φ(n),
从而

(p-3)φ(n)-pτ(n)=
(p-3)(φ(n)-τ(n))-3τ(n)>0.
这就完成了引理2.3的证明.
引理 2.4若
n∈{pt(t≥2,p≥5),pq(q>p≥5),
则
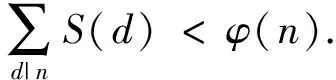
证明若n=pt(t≥2,p≥5),则由
2p<1+3p<(p-1)p=φ(p2),
以及引理2.3可知
若n=pq(q>p≥5),则由
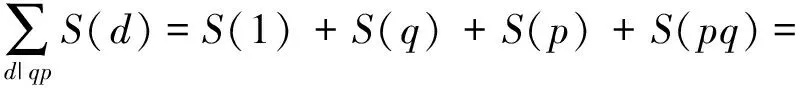
1+p+q+q≤3q-1<
(q-1)(p-1)-2=φ(qp)-2,
可知

若n=3t(t≥4),则由
28<54=φ(34),
以及引理2.3可得
若n=2t(t≥7),注意到
φ(2t)=2t-1.
不妨设
u(t)=φ(2
则
u(7)>0,u′(t)=2t-1ln2-2t-1,
u′(7)>0,u(2)(t)=2t-1ln22-2>0.
故当t≥7时,u(t)>0,所以
若n=2t3s(t≥7,s≥1),断言
为证明断言只需证明
因为
且
2t-1-(4+t+t2)=u(t)>0.
综上,断言得证.由上述断言以及引理2.3可得
这就完成了引理2.4的证明.

证明设
则n=n1n2且
n2(-1)
这就完成了引理2.5的证明.
引理 2.6设α≥2为正整数,p、q均为素数且q>p≥5,则:
1) (p-1)2pα-2>pα+2;
2) (q-2)(p-2)>q+2.
证明1)α=2,3,4,直接计算可知
(p-1)2pα-2>pα+2.
若α≥5,不妨设
v(α)=(p-1)2pα-2-pα-2,
则
v′(α)=(p-1)2ln(α-2)pα-2-p>0,
因而v(α)严格单调递增.又v(5)>0,故v(α)>0,即(p-1)2pα-2>pα+2成立.
2) 由q>p≥5可知
(q-2)(p-2)-q-2=qp-2q-2p-
q+2≥qp-5q+6>0,
即
(q-2)(p-2)>q+2.
这就完成了引理2.6的证明.
3 主要结果的证明

注意到
N+-{1}={n|p(n)≥5}∪{n|p(n)=3}∪
{n|p(n)=2且3⫮n}∪{n|p(n)=2且3|n},
故有以下4种情形:
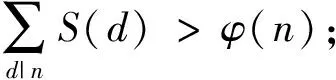
m∈{pt(p≥5,t≥2),pq(q>p≥5)},

m∈{33p,32p(p≥7),32×52,3p2}


A1={2t,t≤6},
A2={24p(p=5,7),23p,22×52}∪
{22p,2p2(p=5,7),2p},
A3={22×5p(p=7,11,13),2×7×11,2×5p},
且ω(Ai)=i,1≤i≤3;否则,存在正整数m|n,其中
m∈{2t|n,t≥7}
且ω(m)=1,或者
m∈{26p,25p,24p(p≥11),24p2(p=5,7),23p2}∪
{22p2(p≥7),22×53,2p2(p≥11),
2p3(p=5,7)}
且ω(m)=2;或者
m∈{24pq(p=5,7),23pq,22×52p,22pq2}∪
{22pq(p≥7),22×5p(p≥17),
2p2q(p=5,7)}∪
{2pq2,2pq(p≥11),2×7p(p≥13)},
且ω(m)=3,其中q>p;或者
m∈{22×5pq(q>p=7,11,13),
2×7×11p,2×5pq},


B1={34×2,33×2t(t≤3),32×2t(t≤4)}∪
{3×2t(t≤6)},
B2={33×2×5,32×23×5,32×2p}∪
{32×22p(p=5,7,11,13),3×25×5}∪
{3×23p,3×24p(p=5,7),3×22×52}∪
{3×22p,3×2p2(p=5,7),3×2p},
B3={3×22×5p(p=7,11,13)}∪
{3×2×7×11,2×3×5p},
且
ω(Bi)=i+1, 1≤i≤3;
否则,存在正整数m|n,其中
m∈{2t3s(t≥7,s≥1),2i×32(i=6,5)}∪
{24×33,2i×34(i=2,3),2×35}
且ω(m)=2;或者
m∈{34×2p,33×2ip(i=2,3)}∪
{33×2p(p≥7),33×2×52,32×24p}∪
{32×23p(p≥7),32×23×52,32×22p2}∪
{32×22p(p≥17),3×23p2,32×2p2}∪
{3×25p2,3×25p(p≥7),3×25×52}∪
{3×24p(p≥11),3×24p2(p=5,7)}∪
{3×2p2(p≥11),3×2p3(p=5,7)}∪
{3×22×53,3×22p2(p≥7)},
且ω(m)=3;或者
m∈{q(B2-{3×22p,3×22pq2})}∪
{3×22pq(p≥7),3×22×5q(q≥17)}∪
{3×2p,3×2pq2,3×2pq(p≥11)}∪
{3×2×7q(q≥13)},
且ω(m)=4,其中q>p;或者
m∈{3×22×5pq(q>p=7,11,13)∪
{3×2×7×11p,3×2×5pq},

推论1.2的证明直接计算可知
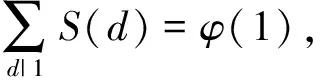
再由定理1.1立得结论.

S(n)=S(pα)=max{S(pi)(i=1,2,…,t),
S(pαii)(i=t+1,t+2,…,m)},
以及
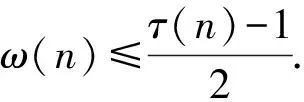
以及
故由引理2.6可知,当d≠1,p时,有
因此
S(d2ω(n)+2)+…+S(dτ(n))=S(1)+
S(d2ω(n)+2)+…+S(dτ(n))<
f(d2ω(n)+2)+…+f(dτ(n))=

φ(n)-(2τ(n)-4ω(n)-2).
这就完成了定理1.3的证明.
4 一些例子
本小节给出几个例子进一步验证本文的主要结果.


2)n=17 640.一方面,因为n=17 640=23×32×5×72,3|n,p(n)=2,ω(n)=4,n∉B3,所以

另一方面,因为




另一方面,有

S(2p)+S(3p)+S(6p)+S(q)+S(2q)+
S(3q)+S(6q)+S(pq)+S(2pq)+S(3pq)+
S(6pq)+S(γ)+S(2γ)+S(3γ)+S(6γ)+
S(pγ)+S(2pγ)+S(3pγ)+S(6pγ)+S(qγ)+
S(2qγ)+S(3qγ)+S(6qγ)+S(pqγ)+
S(2pqγ)+S(3pqγ)+S(6pqγ)=
9+4p+8q+16γ<48γ-48≤
2(p-1)(q-1)(γ-1)=φ(6pqγ),


