时滞重随机线性二次最优控制问题

许 洁, 陈 岩

(1.吉林化工学院 理学院, 吉林 吉林 132022; 2. 吉林大学 数学学院, 吉林 长春 130012)

0 引言

时滞是自然界中广泛存在而又不可避免的一种现象,在时滞问题的研究中,过去的历史对解决当前问题的发展起到至关重要的作用,如果忽略掉时滞的存在，会使问题无法解决或解决的结果与实际具有一定偏差.对一个系统而言,当观测与调控之间有时间差或者控制有滞后性时，就会出现系统延迟,我们称之为时滞系统,刻画含有时滞状态的方程称为时滞方程.系统中时滞变量的存在会引起系统相应性能的变化,许多工程理论问题相继出现,并迫切需要解决,为时滞控制理论的发展注入动力[1-5].最大值原理为求解最优控制问题做出巨大贡献,如何利用最大值原理的思想，结合时滞系统的特点,更好地刻画时滞系统的最优控制问题成为研究的关键.文献[6]中讨论了一类被称为超前倒向随机微分方程的新型倒向随机微分方程,为解决时滞问题提供新的思路.文献[7]利用此类方程对倒向随机系统的时滞问题进行研究,给出了时滞系统的最优控制所满足的必要条件，并将其应用到消费生产模型,得出最优消费率的显示表达式.受此研究思路的启发,我们尝试对线性时滞二次最优控制问题进行探索,希望对此时系统对应的最优控制的形式进行刻画.

1 准备工作

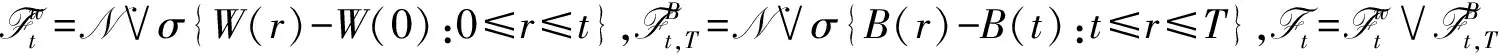
时滞重随机微分方程的一般形式为：

(1)

根据实际问题的不同,f和g取不同的形式.讨论时滞重随机线性系统,设系统对应的状态方程为:

(2)

其中δ1、δ2和δ3是不同的时滞变量.

目标泛函为

〈R(t)y(t),y(t)〉+〈S(t)u(t),u(t)〉]dt+

〈Qx(T),x(T)〉}.

(3)

定义

U[0,T]:=

最优控制问题可以看成在U[0,T]上最小化目标泛函,即寻找最优控制u*(·)使其满足

J(u*(·))=

(4)

此时对应的(x*(·),y*(·),u*(·))被称为最优三元组.

对应地,此时系统的伴随方程为

(5)

其中δ=max{δ1,δ2,δ3}.

给出假设条件：

(A1) 假设系数矩阵Ai,Bi,Ci,Di,Ei,Fi(i=1,2)是适当维数的矩阵过程；

(A2) 设Q:Ω→Rn×n是非负有界对称Ft适应矩阵过程；

(A3) 所有系数矩阵均有界,且K(t)、R(t)和Q是对称非负正定的,S(t)是对称一致正定的.

讨论线性系统,由假设条件(A3)可知,所有关于f、g的偏导数都是有界的,且f和g直接满足Lipschitz条件,这使得我们的假设变得简单了很多.

2 主要结论

定理 1在假设条件(A1)～(A3)下,

E

是时滞重随机线性二次最优控制问题的唯一最优控制,其中(x*(·),y*(·),p(·),q(·))是对应(2)和(5)式的解.

证明方程(2)解的存在性和唯一性可以由文献[8]中的定理3.1直接推得.方程(5)解的存在性和唯一性可以由文献[9]的定理3.2保证.首先证明u*(t)是系统对应的最优控制.对任意的v(·)∈U[0,T],设(x*(·),y*(·))、(xv(·),yv(·))分别是对应控制u*(t)和v(t)的轨迹,则

J(v(·))-J(u*(·))=

〈K(t)x*(t),x*(t)〉+

〈R(t)yv(t),yv(t)〉-

〈R(t)y*(t),y*(t)〉+〈S(t)v(t),v(t)〉-

〈S(t)u*(t),u*(t)〉+

〈Qx(T),x(T)〉-〈Qx*(T),x*(T)〉]dt=

xv(t)-x*(t)〉+

〈S(t)(v(t)-u*(t)),v(t)-u*(t)〉+

〈R(t)(yv(t)-y*(t)),yv(t)-y*(t)〉+

〈Q(xv(T)-x*(T)),xv(T)-x*(T)〉+

2〈K(t)x*(t),xv(t)-x*(t)〉+

2〈R(t)y*(t),yv(t)-y*(t)〉+

2〈S(t)u*(t),v(t)-u*(t)〉+

2〈Qx*(T),xv(T)-x*(T)〉]dt.

(6)

由条件(A3)知道K(t)、R(t)和Q是对称非负定的,S(t)是对称且一致正定的,因此

J(v(·))-J(u*(·))≥

〈S(t)u*(t),v(t)-u*(t)〉+

〈R(t)y*(t),yv(t)-y*(t)〉+

〈Qx*(T),xv(T)-x*(T)〉]dt.

(7)

应用Ito公式并注意其初始条件和终端条件,可得

〈Qx*(T),xv(T)-x*(T)〉=

〈-p(T),xv(T)-x*(T)〉,

E〈p(T),xv(T)-x*(T)〉=

B1(t)(xv(t-δ1)-x*(t-δ1))+

C1(t)(yv(t)-y*(t))+

D1(t)(yv(t-δ2)-y*(t-δ2))+

E1(t)(v(t)-u*(t))+

F1(t)(v(t-δ3)-u*(t-δ3))〉dt-

E

E

K(t)x*(t),xv(t)-x*(t)〉dt+

B2(t)(xv(t-δ1)-x*(t-δ1))+

C2(t)(yv(t)-y*(t))+

D2(t)(yv(t-δ2)-y*(t-δ2))+

E2(t)(v(t)-u*(t))+

F2(t)(v(t-δ3)-u*(t-δ3))〉dt+

E

yv(t)-y*(t)〉dt.

(8)

x*(t-δ1))〉-〈E

xv(t)-x*(t)〉}dt=

B1(t)(xv(t-δ1)-x*(t-δ1))〉dt-

类似可有

〈E

x*(t)〉}dt=0,

〈E

y*(t)〉}dt=0,

〈E

y*(t)〉}dt=0.

因此，可得

E〈-p(T),xv(T)-x*(T)〉=

〈-R(t)y*(t),yv(t)-y*(t)〉+

〈-p(t),E1(t)(v(t)-u*(t))+

F1(t)(v(t-δ3)-u*(t-δ3))〉+

〈-q(t),E2(t)(v(t)-u*(t))+

F2(t)(v(t-δ3)-u*(t-δ3))〉]dt.

(10)

则

J(v(·))-J(u*(·))≥

〈-p(t),E1(t)(v(t)-u*(t))+

F1(t)(v(t-δ3)-u*(t-δ3))〉+

〈-q(t),E2(t)(v(t)-u*(t))+

F2(t)(v(t-δ3)-u*(t-δ3))〉]dt.

(11)

由u*(t)的定义,可得

E

将其代入不等式(11),可得

J(v(·))-J(u*(·))≥

E

〈-p(t),E1(t)(v(t)-u*(t))+

F1(t)(v(t-δ3)-u*(t-δ3))〉+

〈-q(t),E2(t)(v(t)-u*(t))+

F2(t)(v(t-δ3)-u*(t-δ3))〉}dt=

〈-p(t),F1(t)(v(t-δ3)-

u*(t-δ3))〉+〈-q(t),F2(t)(v(t-δ3)-

u*(t-δ3))〉}dt.

(12)

类似前面的证明可得

u*(t)〉+〈-p(t),F1(t)(v(t-δ3)-

u*(t-δ3))〉}dt=0,

u*(t)〉+〈-q(t),F2(t)(v(t-δ3)-

u*(t-δ3))〉}dt=0，

因此，有

J(v(·))-J(u*(·))≥0.

对任意v(·)∈U[0,T]成立,则可证得u*(t)是最优控制.

J(u1(·))=J(u2(·))=α≥0,

则

2α=J(u1(·))+J(u2(·))=

再由S(t)的正定性,可推得u1(·)=u2(·),唯一性得证.定理1证毕.

由定理1的结论可知,系统的最优控制是与控制中的时滞变量有关,那么如果控制变量中不含有时滞变量,可以直接得到下面的推论.

推论 1假设(A1)～(A3)成立,则

t∈[0,T]

是时滞重随机线性二次最优控制问题的唯一最优控制,其中(x*(·),y*(·),p(·),q(·))是系统

的解,其中δ=max{δ1,δ2}.

证明此推论的证明可以由定理1直接推得,当δ1=δ2时,也可以由文献[8]的最大值原理直接推得.本文结论讨论了时滞变量各不相同的情况,推广了文献[8]的部分结果.

由上面的结论可以发现，最优控制的形式与伴随方程的解具有密切关系,这是一类新型的超前重随机微分方程,本文利用此类方程的解对最优控制的形式进行了刻画.

为了更好地研究时滞问题,可尝试从不同角度对此类问题进行探索,文献[10]利用Riccati方程对一类随机哈密顿系统的解进行研究,受此研究思路的启发,利用Riccati方程对时滞重随机系统的最优控制形式进行研究,从定理1的结论中,发现控制变量中的时滞变量对系统最优控制的形式具有重要的作用,讨论一个特殊的系统,只考虑控制变量中含有时滞的情况，且状态变量的初值η是确定性的.

此时的时滞系统可以写成

仍然探讨目标泛函是(3)式的最优控制问题(4),利用定理1可以直接得出此时系统对应的最优控制形式,即

u*(t)=

S-1(t)E

t∈[0,T].

(16)

下面借助Riccati方程的解对最优控制的形式进行探索,首先定义此系统对应的Riccati方程:

(17)

定理 2在假设条件(A1)～(A3)下,如果Riccati方程(17)的解(G(·),M(·),N(·))存在,则系统(15)具有唯一解(x(t),y(t),p(t),q(t))=(x(t),G(t)x(t),M(t)x(t),N(t)x(t)),其中x(t)是下面方程的解,

C1(t)y(t)+F1(t)u(t-δ)]dt+

M(t)[A2(t)x(t)+C2(t)y(t)+

F2(t)u(t-δ)]dW(t)-M(t)y(t)dB(t).(19)

将Riccati方程(17)中的第一和第二个方程代入到(19)式,可得

dW(t)-M(t)y(t)dB(t).

(20)

再由Riccati方程(17)可知

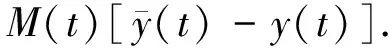
(21)

则(20)式可以写成

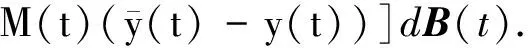
(22)

(23)

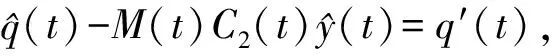
(24)

定理 3在假设条件(A1)～(A3)下,设(G(·)、M(·)和N(·))满足Riccati方程,则时滞重随机线性二次最优控制问题的最优控制具有如下形:

(25)

且

(26)

证明由已知(G(·)、M(·)和N(·))是Riccati方程(17)的解,且令y(t)=G(t)x(t),p(t)=M(t)x(t),q(t)=N(t)x(t).对p(t)应用Ito公式,可得

M(t)C1(t)y(t)+M(t)F1(t)u(t-δ)]dt+

[M(t)A2(t)x(t)+M(t)C2(t)y(t)+

M(t)F2(t)u(t-δ)]dW(t)-

M(t)y(t)dB(t),t∈[0,T].

(27)

再由Riccati方程(17),有

M(t)A1(t)x(t)+M(t)C1(t)y(t)+

M(t)F1(t)u(t-δ)}dt+

{[N(t)-M(t)C2(t)G(t)-

M(t)F2(t)u(t-δ)}dW(t)-

(28)

即

K(t)x(t)]dt+[R(t)y(t)-

q(t)dW(t),t∈[0,T].

(29)

因此，系统(15)的解满足公式y(t)=G(t)x(t),p(t)=M(t)x(t),q(t)=N(t)x(t),则最优控制可直接由(25)式给出.

下面利用Riccati方程的解以及状态变量的初值条件给出对应最优控制的目标泛函J(u*(·)).对〈x(t),p(t)〉应用Ito公式并取期望,可得

E[〈x(T),p(T)〉-〈x(0),p(0)〉]=

E[〈x(T),-Qx(T)〉-〈η,M(0)η〉],

(30)

E[〈x(T),p(T)〉-〈x(0),p(0)〉]=

〈F1(t)u(t-δ),p(t)〉+

〈F2(t)u(t-δ),q(t)〉]dt=

EFt〈F2(t+δ)u(t),q(t+δ)〉+

〈K(t)x(t),x(t)〉+〈R(t)y(t),y(t)〉]dt.(31)

将(30)和(31)式代入J(u(·)),可得

〈R(t)y(t),y(t)〉+〈S(t)u(t),u(t)〉]dt+

(32)

定理3证毕.

本文从不同角度对时滞重随机线性二次系统最优控制问题的最优控制形式进行了刻画,根据实际问题的不同,采用不同的研究方法,可以从不同角度更好地解决问题.