基于等级邻域策略的偏序柔性车间优化调度*

李长云 林 多 何频捷 谷鹏飞

（①湖南工业大学计算机学院，湖南 株洲 412007；②湖南工业大学轨道交通学院，湖南 株洲 412007）

柔性作业车间调度问题[1](flexible job shop scheduling problem，FJSP)是一种研究生产资源的分配与工件工序的加工顺序的问题，具有加工设备不确定和工艺路线柔性等特性。在实际的车间生产环境中，很多工件的工艺流程具有偏序关系，可能会包含工序具有共同前继工序或者多个前继工序的情况，以服装生产车间为例[2]，在布料裁剪阶段之后可以由不同机器并行完成服装不同部位的缝制，最后再统一进行拼接和后续操作。提高工序的并行性并考虑前继工序的约束性，能够实现具有偏序工艺流程的柔性车间调度，提高工厂资源的利用效率。

国内外学者对FJSP的研究主要集中在机器柔性和顺序工艺流程的问题，对具有复杂偏序关系的FJSP研究较少。其中，谢志强等[3−4]针对串行工序的紧密度和并行工序的并行性提出考虑后续工序的择时综合调度算法。唐红涛等[5]针对包含并行工序集的车间提出动态触发邻域机制增强算法的局部搜索能力。刘晓平等[6]提出了工序和设备分段编码从而实现适应工件工序可并行的解码算法，缩短了最大完工时间。徐本柱等[7]研究了工序的并行特性，有效地缩短了产品完工时间。以上算法大都对复杂的并行工序情况考虑不全面，没有有效地解决串行工序的紧凑度和并行工序的并行性之间的关系，同时未考虑瓶颈工单和瓶颈机器中工件的偏序关系对最小化完工时间的影响。

本文针对偏序柔性作业车间调度问题(partial order flexible job-shop scheduling problem，POFJSP)提出了改进的算术优化算法(improved arithmetic optimization algorithm,IAOA)，设计了基于适应度和工序完工差异度的二维聚类交叉和有效变异策略，并引入一种等级邻域变异策略对瓶颈工单和瓶颈机器上的工序分等级进行变异，有效地缩短了具有偏序关系工件的最大完工时间。最后通过仿真实验对比其他优化算法验证本文所提算法的可行性和优越性。

1 问题模型描述和约束建立

1.1 偏序柔性车间调度问题描述

FJSP中工件工序按照顺序关系调度[8]，每个工序在加工机器集中选择一个机器进行生产。服装车间中工件的生产需要经过多个工序的加工，每个工序可由一个或多个机器进行加工，每个工序存在一个或多个前继工序。因此服装车间的调度问题和FJSP比较类似，但是需要考虑工件加工具有复杂偏序工艺流程的特点。故将服装车间的调度问题抽象为POFJSP，该问题是FJSP的衍生，针对工件的生产工艺流程通常不是顺序型工艺流程，而是具有偏序关系的生产加工关系调度进行研究。

该问题可以采用如下描述：每台机器完成不同的工单工序所花费的时间不同，每个工单加工产品的工艺流程不同，假设共有n个工单Job={J1,J2,J3,···,Jn}，每个工单Ji(1≤i≤n)包含pi个工序O={Oi1,Oi2,Oi3,···,Oip}，工单工序可以在m个机器M={M1,M2,M3,···,Mm}上进行生产，若工单工序在某些机器Mk(1≤k≤m)上不能生产，则对应的生产时间为空。一个工件的工序可能具有一个或多个前继工序以及后继工序，工序Oij具有前继工序集Fij和后继工序集Sij。工序的加工时间要介于前继工序与后继工序之间，并具有严格的加工次序约束。

工件工艺流程如图1所示，工件J1的工艺流程中工序O12,O13,O14拥有共同的前继工序O11，工序O11的后继工序集S11={O12,O13,O14}可并行加工；工序O26有多个前继工序O24,O25，其最早开始时间为前继工序集F26={O24,O25}中结束时间ET24,ET25较晚的值。

图1 工件工艺流程图

1.2 数学模型建立

针对偏序柔性车间调度问题，本文基于以下假设建立数学模型：

（1）零时刻可加工所有工件的第一个工序，且所有机器属于待工状态。

（2）一台机器上不能同时加工多个工序。

（3）同一个工件的前继工序全部加工完成后才能开始下一道工序。

（4）某工件一旦在某机器上开始加工，不可中断当前工序的运作。

（5）工件加工互不影响，机器加工互不影响。

为了后续描述表达方便，现将各变量定义如表1所示。

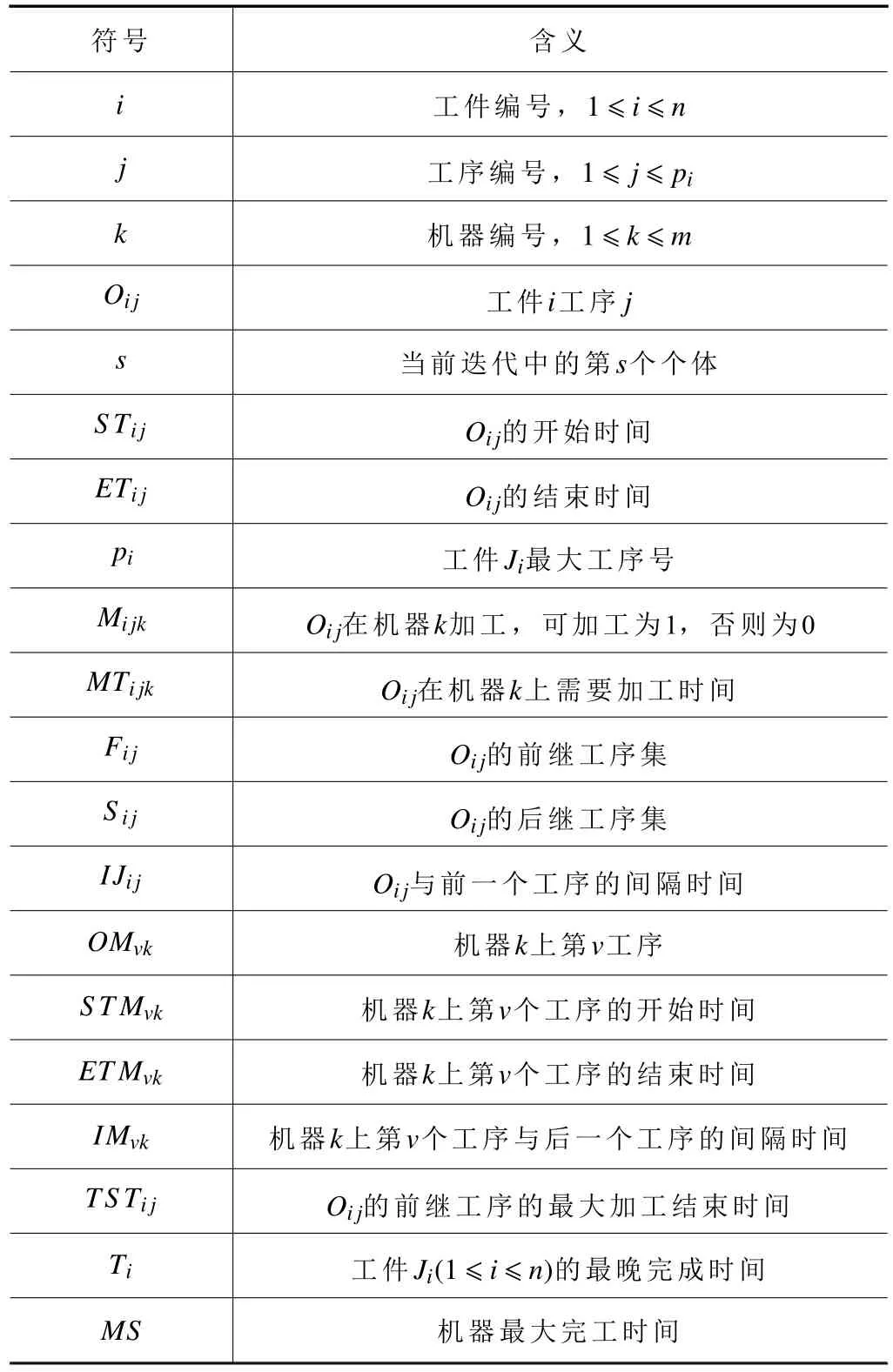
表1 符号及其描述

本文研究的优化目标为最小化机器最大完工时间[9]，基于上述假设条件和数学符号描述模型约束

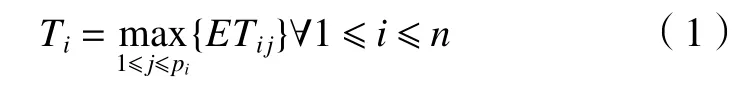
其中：式（1）表示工件Ji（1≤i≤n）的最大完工时间；式（2）表示优化目标为最小化机器最大完工时间，即适应度；式（3）表示工件的每道工序只能在一台机器上加工；式（4）表示工件工序含有一个或者多个前继工序，规定工单开始工序的前继工序为空；式（5）表示工件的结束工序不包含后继工序（置为空集），其他工序的后继工序集中包含一个或多个工序；式（6）表示需要完成当前工单工序的全部前继工序后才开始加工；式（7）表示Oij的最早结束时间为其前继工序的完成时间的最大值与其所在加工机器上的加工时间之和；式（8）表示机器加工当前工序完成之后才能开始下一个工序的加工。

2 基于等级邻域策略的改进算术优化算法（IAOA+GNS）设计

算术优化算法(arithmetic optimization algorithm,AOA)[10]是一种群智能算法，用于解决连续型运筹优化问题，具有调整参数少，收敛速度快等优点，其思想适用于解决偏序柔性车间调度问题。在原始的AOA中，将其分为两个主要阶段：勘探和开发。在勘探阶段算法先对搜索空间进行广泛覆盖搜索，以避免陷入局部解，开发阶段对勘探阶段得到的解进行邻域搜索，算法步骤如下。

Step1：设定种群迭代次数T，种群大小popsize，随机初始化生成一组候选解X(1)。首先解码根据式（2）计算种群适应度MS，并将当代种群的最佳候选解视为目前获得的最佳解Xbest(t)，然后通过式（9）计算MOA(t)进行阶段选择。MOA(t)为选择概率，Min为最小概率，Max为最大概率，本文设定Min=0.2，Max=1，随着迭代次数的增加，选择开发阶段概率逐渐大于勘探阶段。

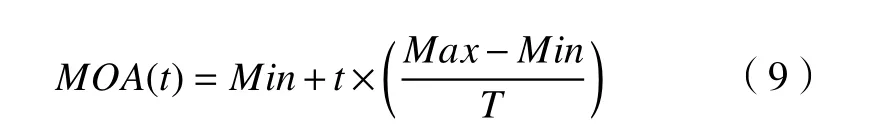
Step2：勘探阶段，在Xbest(t)附近使用搜索策略在多个解空间上进行随机搜索，从而扩大种群多样性。

Step3：开发阶段，利用搜索策略在适应度值较高的解邻域进行深入搜索，并在经过多次迭代之后发现接近最优的解。

AOA算法主要用于求解连续型问题，本文研究的POFJSP属于离散型问题，因此提出一种基于偏序工序的改进算术优化算法（IAOA），其次在勘探阶段设计了基于适应度和工序完工差异度的二维聚类交叉和有效并行变异策略增加种群多样性，在开发阶段设计了一种等级邻域搜索（grade neighborhood search，GNS）策略增强算法的局部搜索能力。最后结合两者提出基于等级邻域策略的改进算术优化算法（IAOA+GNS）求解POFJSP。

基于等级邻域变异策略的改进算术优化算法流程如图2所示。

图2 IAOA+GNS算法流程图

2.1 编码解码

POFJSP需要考虑到工件工序以及生产机器的安排，本文采取双编码形式Xi(t)=[Xg|Xm]对工序和机器进行编码，Xg为工序编码部分，工件Ji出现的次数为其第j个工序，Xm为机器编码部分，表示对应工序Oij的可选机器集中的机器编号Mijk。编码形式如图3所示。

图3 编码示例图

解码是群智能算法能否解决车间调度问题的关键，考虑解码的多约束性并通过工件前继工序和机器可用时间段可以确定后继工序的最优加工时间，IAOA进行解码时具有以下步骤：

Step1：将候选解Xi(t)的工序编码部分换算为工件工序Oij列表，找到对应的安排机器Mijk。

Step2：将前继工序为空集的工序的最早可开始时间TSTij初始化为0，其他的工序则按照式（6）计算其TSTij。

Step3：对Oij使用基于插入优先的解码策略：当Oij安排的Mijk上已安排的工序数大于0时，转到Step3.1，否则转到Step3.3。

Step3.1：判断Oij能否插入到Mijk上的第一个工序前，如果第一个工序的开始时间STM1k大于等于Oij的TSTij和其加工时间MTijk之和，则跳转到Step4，否则判断Mijk上已安排的工序数是否大于1，是则跳到Step3.2，否则跳到Step3.3。

Step3.2：循环安排在Mijk上，且时间在Oij的TSTij之后的所有工序OMvk，使用式（8）计算两个工序之间的时间间隔IMvk，在Oij的TSTij和工序OMvk的结束时间ETMvk中选择较大的值，判断该值和Oij的加工时间MTijk之和是否小于下一个工序的开始时间STM(v+1)k，并且IMvk是否大于等于Oij的MTijk，是则表示可以插入该空闲时间段，转到Step4。循环完毕，如发现没有可插入的时间段，则跳转到Step3.3。

Step3.3：Oij不能插入Mijk上的空闲时间段，在Oij的TSTij和Mijk上已安排的最后一道工序的结束时间ETMvk中选择较大的值，该值即为Oij的真正开始时间STij。

Step4：利用式（1）和式（2）算出目标函数值。

如图4所示，有3个具有偏序关系的工件，将部分工序按照解码步骤解码到调度甘特图，以工序O22为例，其TSTij=3，机器M1安排工序数大于2，转到Step3.2检查空位1发现IM12≥MT221但MT221+TST22≤STM21，检查空位2发现IM22≥MT221且ETM21+MT221≤STM31，符合条件，可插入空位2。

图4 解码调度甘特图

2.2 种群初始化

种群初始化的质量好坏直接影响到算法求解速度和最终解的质量，为了减少无效解的产生并增加种群多样性，采用以下两种方法进行种群初始化（两种方法生成的初始解在初始种群数量中各占50%）。

正向法：首先随机打乱工序编码，并为每道工序随机分配机器，随后通过前继工序表查看所有工序，将具有共同前继工序的工序编码排在一起，最后检查同一工单中具有共同前继工序的工序的机器编码，如果在同一台机器上加工，则在可选机器集中重新选择机器进行分配。

逆向法：由正向法生成的工件编码通过倒置得到逆向编码，机器编码仍采用正向法编码规则随机生成。

2.3 勘探阶段

IAOA算法在传统AOA算法上融合了GA算法的思想，将搜索策略替换成了交叉和变异，以此解决离散调度问题，因此在勘探阶段中使用二维聚类交叉策略和有效并行变异策略扩大种群多样性。

2.3.1 二维聚类交叉策略

本文使用聚类交叉方法进行操作，由于不同适应度值的两类个体基因存在相似可能性，因此对种群内每个个体引入工序完工差异度（degree of variance of process completion,DVPCs），DVPCs可以计算出不同个体基因之间的差异度，结合适应度值组成二维聚类再进行交叉增大种群多样性。工序完工差异度计算式（10）如下。

首先以当前迭代种群最优个体Xbest作为基准，对种群中所有个体的适应度MSs和DVPCs统一进行最大最小归一化，范围为[0,1]，并以MSs和DVPCs作为指标绘制散点图。随后使用k-means聚类算法对种群进行二维聚类，其中参数k为聚类的数量，本文将k设为4，对应不同MSs和DVPCs下的个体类，聚类算法结果如图5所示。

图5 适应度和完工差异度聚类图

随后随机选择两类中的个体作为父代，保留其中适应度较小的父代中的优秀基因，优秀基因为个体基因中工单紧凑度（work order compactness，WOC）高的工单，WOC可通过比较工单理想完成时间和工单实际完成时间获得，如式（11）所示。

优秀基因的保留能够加快迭代速度并优化子代基因以获取更优解。最后使用POX交叉将父代P1的优秀基因保留，其他基因删除，并将另一父代P2中除了优秀基因工单外的其他工单从左到右依次填补到P1的空基因位上得到交叉后的子代基因。

2.3.2 有效并行变异策略

针对变异过程中可能存在的无效变异问题，本文对机器变异和工序变异进行了以下改进。

机器变异：随机选择总数量中20%的工序，将其对应机器换成可选机器集中加工时间更短的机器进行加工。

工序变异：针对不同机器上的工序进行位置交换可能对该机器的加工工序数量和顺序不具有任何影响，从而导致无效变异的问题。本文对同一台机器上加工的任意多个工序交换位置，可有效减少无效变异。

2.4 开发阶段

影响适应度函数的直观原因在于以下两点：一是瓶颈工单的WOC在所有工单的WOC中处于较低值，大部分工序在对应机器上的加工时间比较长，且与前继工序之间的时间间隔较大；二是瓶颈机器上的利用率远高于其他机器，瓶颈机器上加工的工序将对目标函数值起到决定作用。

基于上述问题，开发阶段在多个密集解空间上深入搜索最优解，使用等级邻域搜索策略（GNS）分别对瓶颈工单和瓶颈机器两个方面进行邻域搜索。GNS策略如下：

（1）优先级设定。首先为不同情况下的工序设定优先等级，具有多个后继工序的工序在机器上的完成时间能够影响到所有后继并行工序的完成进度，是缩短工单的最大完工时间的重要因素，因此该类工序为最高优先级G1；多数工序只存在一个后继工序，可以通过对该类工序使用优化策略缩小目标函数值，因此设为中等优先级G2；最后一道工序对整个工单的完成时间影响不大，设为最低优先级G3。

（2）变异策略设定。针对不同原因对工序进行不同的变异策略，分为以下3种情况讨论。

GNS1：如果当前工序的开始时间和前继工序的完成时间间隔大于当前工序加工时间的一半，则将当前工序与对应机器上其前继工序完成时间之后开始加工的其他工序随机进行位置互换；

GNS2：如果当前工序与前继工序的时间间隔较小，则将当前工序换到可选机器集中加工时间更少的机器；

GNS3：如果当前工序所处机器上没有空闲时间段，则将当前工序交换至可选机器集中机器负载更小的机器上。

若同时满足多种情况，则随机选择一种情况进行变异。

（3）瓶颈工单或瓶颈机器变异。对瓶颈工单或瓶颈机器中的所有工序进行优先级排序，随后使用轮盘赌算法按照优先级随机挑选10%工序，并根据不同情况进行变异。

以图4所示的解码调度甘特图为例，假设在第t次迭代中对瓶颈工件J3进行等级邻域变异，其中O31的优先级最高有多个后继工序S31={O32,O33}，使用GNS3策略选择可选机器集中负载更低的机器M1进行加工，得到的调度甘特图如图6所示，有效地提前了工件J3的部分工序加工时间。

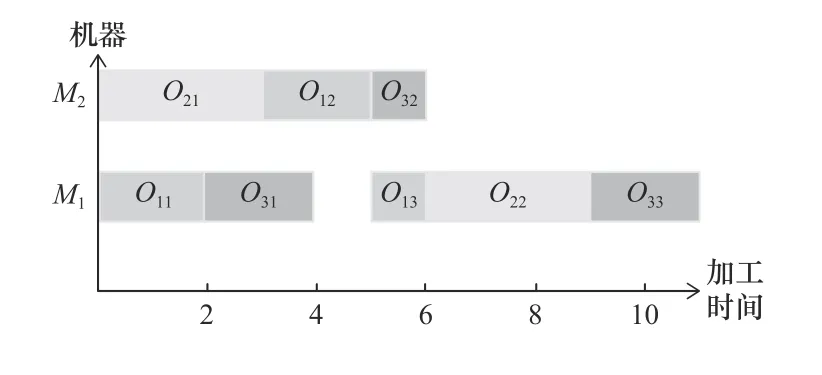
图6 瓶颈工件使用等级邻域策略结果图

假设在第t+1次迭代中对瓶颈机器M1上的加工工序进行等级邻域变异，采用GNS1策略对工序O22与其前继工序的完成时间之后开始加工的工序O13进行位置交换，调度甘特图如图7所示，最大完工时间从原先的11有效地缩短到10。

图7 瓶颈机器使用等级邻域策略结果图

3 仿真实验与案例分析

目前没有标准算例验证本文的研究问题，因此本文基于Brandimarte P[11]所提出的10个案例Mk01～Mk10拓展了适用于偏序柔性车间调度问题的测试算例，表2为生成的扩展算例的参数，新算例PMk01～PMk10在基准算例的基础上添加了每个工序的前继工序集合，为了表达方便，假设每个算例中工件的工艺流程一样。

表2 扩展算例参数

3.1 参数对比实验

智能优化算法的优化结果受算法参数的影响很大，影响算法性能的参数有：种群规模popsize，最大迭代次数T，本文实验所用算法均采用相同参数值。以PMk09为测试算例，选择规模为(32)的正交实验进行测试，为避免结果的随机性，以30次结果的平均值作为评价指标，正交实验结果如表3所示。

表3 正交实验结果比较表

可以从表中看出当种群规模popsize=90，最大迭代次数T=70时算法的性能最好，但是当群规模popsize=90，最大迭代次数T=60时算法效果已经接近最优性能，且运行时间少于达到最优性能所花费的时间，所以本文选择群规模popsize=90，最大迭代次数T=60作为PMk09算例的最优参数。

3.2 算法比较及结果

为了证明本文的IAOA+GNS算法应用在偏序柔性车间调度上的有效性，将本文所采用的方法与文献[12]和文献[13]的算法求解效率进行对比，对比算法的参数与本文算法的一致。同时为了验证本文等级邻域策略的有效性，选择与去掉GNS策略采用传统变邻域搜索的IAOA+VNS算法进行对比，其中IAOA+VNS算法参数与IAOA+GNS一致。仿真软件使用MATLAB 2016a，电脑硬件参数为：处理器 Intel(R) Core(TM) i5-4210U CPU @ 3.70 GHz，内存8 GB。算法各运行30次，并使用运行结果中的最小完工时间Rbest、平均完工时间Ravr、完工时间标准差Rσ和算法平均运行时间评测算法性能。

根据表4的仿真结果可以分析出本文的IAOA+GNS算法应用在偏序柔性车间调度具有较好的效果，最小完工时间和平均完工时间均优于其他优化算法，且完工时间标准差少于其他算法，说明本文算法能够得到更优解，且更稳定性。同时基于IAOA+GNS与IAOA+VNS算法的对比试验可以说明GNS策略的有效性。

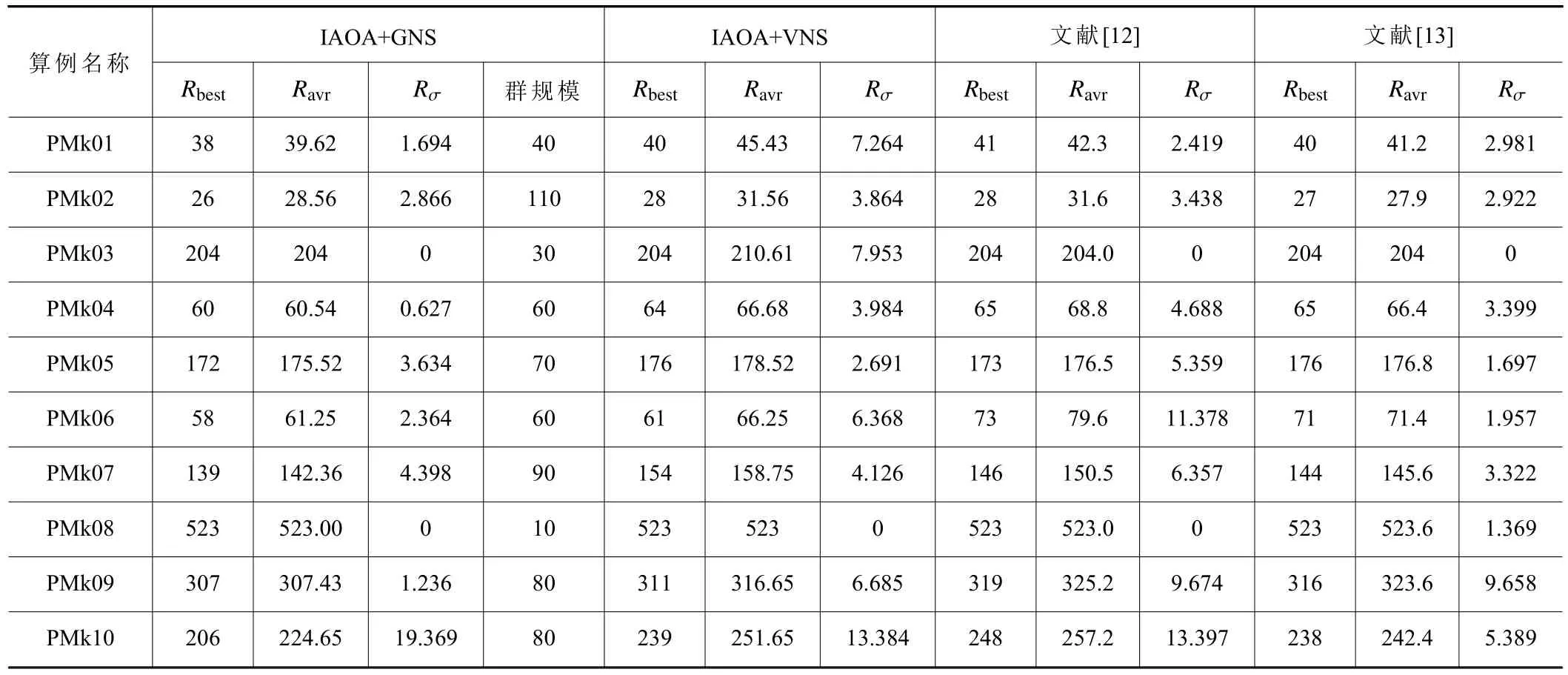
表4 算法效果比较

根据表5的算法平均运行时间来看，算例PMk05、PMk07、PMk09在本文的运行时间比其他算法运行时间更短，最小化最大完工时间也更短。在PMk08算例中大部分工序只能在同一台机器上进行加工，其适应度函数取决于在此机器上加工的工序完成时间，因此无法体现本文算法的优越性。在其他算例中本文算法比其他优化算法的平均运行时间更长，但是本文算法的运行结果更优，且运行时间在可允许范围之内。同时，IAOA+VNS算法比IAOA+GNS算法运行时间少很多，但是其算法稳定性相较于较差，体现了本文改进的IAOA+GNS算法在稳定性上的优势。综上所述，本文算法在解决偏序柔性车间调度问题上相较于现有其他几个算法在性能和稳定性上更优越。

表5 算法平均运行时间

以算例PMk09为例，图8展示了本文算法对该算例的调度甘特图，从图中可以看出，其最大完成时间为307，8号机器为瓶颈机器，该机器上已无空闲时间可进行调度，限制了适应度函数的最小值。

图8 算例PMK09调度甘特图

4 结语

针对服装加工行业中工件具有复杂工艺流程的情况，本文提出了IAOA+GNS算法求解该类偏序柔性车间调度问题。算法充分考虑了前继工序的约束性，首先基于适应度和工序完工差异度设计出聚类交叉和有效变异策略，避免无效变异的同时扩大了种群探索范围；然后利用瓶颈机器和瓶颈工件的关键性进行等级邻域变异以搜索更优解。通过仿真实验对比其他算法，验证了IAOA+GNS算法的有效性和稳定的求解性能。接下来将下一步的研究重点放到动态调度偏序柔性车间调度上。