基于自适应遗传模拟退火算法的多目标车间布局优化*

卢义桢 李西兴 朱传军 吴 锐

（①广东工业大学管理学院，广东 广州 510000；②湖北工业大学现代制造质量工程湖北省重点实验室，湖北 武汉 430068）

车间设施布局问题是智能制造精益生产中面临复杂问题之一，其实质是一种非线性组合优化问题，需要寻求合理高效的车间设施布局方案来提高车间空间利用率，降低车间物流成本，提高生产效率。车间设施布局是否合理对整个生产系统的总体性能有着重要的影响。

当前车间布局优化问题主要利用智能优化算法进行求解。国内研究中，谢洁明等[1]提出了基于仿真的遗传网格自适应直接搜索算法（GMADS）用于求解具有单向导向路径网络、多重嵌套封闭环形物料储运系统的布局优化问题。郭源源等[2]采用粒子群算法求解二维设施布局问题并将粒子群算法与SLP法进行结合，提高了初始解的合理性和寻优过程的高效性。陈勇等[3]为满足低成本、高稳健性的车间布局要求，设计了以单位面积布置成本、单位产品物流成本和布局熵为优化目标的车间布局优化模型，提出了基于Pareto优化的聚类并行多目标遗传算法。国外学者对应用智能算法求解布局问题也有诸多研究，Frederico Galaxe Paes等[4]通过引入经分解策略改进后的遗传算法解决不平等区域设施布局问题（UA-FLP）时，寻优表现优于普通遗传算法。Jose Fernando Goncalves等[5]针对不平等区域设施布局问题提出了偏向性的随机关键遗传算法（BRKGA）确定设施布局方案。

在车间设施布局优化研究中，多将车间不同作业单元间搬运距离总和作为优化目标[6−7]，而没有考虑到实际生产中不同作业单元之间物料搬运方式可能存在差异的情况针对该问题，本文考虑不同作业单元之间物料搬运方式不同的情况，以最小车间物流成本与最短车间搬运时间为优化目标，采用自适应遗传模拟退火算法对车间设施布局问题进行求解，并通过实例分析验证了模型和算法的有效性。

1 问题描述

在制造车间中，零件按各自批量和工艺流程依次经过不同的作业单元完成加工过程。在这个过程中，不同的车间设施布局方案会对物料搬运过程的时间、成本等指标产生影响，需要建立数学模型，通过运算求解出一套较优的布局方案以满足降低生产成本、提高生产效率的要求。

1.1 问题假设

（1）假设各作业单元形状均为标准矩形，长和宽均已知。

（2）假设各作业单元均为横平竖直，作业单元的边界分别平行于车间四周边界。

（3）假设物料是从一个作业单元的几何中心搬运到下一个作业单元的几何中心。

（4）假设物料搬运的路径平行于车间边界的直线。

（5）假设不同作业单元之间物料搬运速度不同且均已知。

基于以上假设，建立车间设施布局示意图如图1所示。

图1 车间设施布局

在图1中，X轴为车间的长度方向；Y轴为作业车间的宽度方向；mi为车间第i个作业单元，i=1,2,···,N（N为车间作业单元总数）；L为作业车间总长度；W为作业车间总宽度；li、wi分别为车间i作业单元的长度、宽度；xi、yi分别为i作业单元几何中心点的横坐标、纵坐标；sij为i作业单元与j作业单元边界之间的净间距[8]。

1.2 数学模型

本文同时考虑车间物流成本最小与车间搬运时间最短两个目标进行建模，目标函数表达式如下所示。

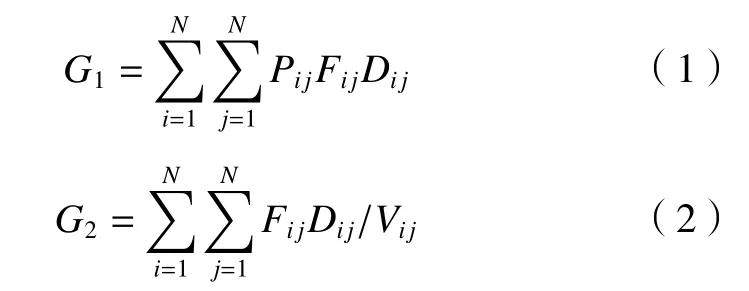
式中：G1为第一个优化目标车间物流成本；G2为第二个优化目标车间搬运时间；Pij为i作业单元与j作业单元之间单次物料搬运单位距离的费用；Dij为i作业单元与j作业单元几何中心点之间的曼哈顿距离；Fij为i作业单元与j作业单元之间物料搬运频率；Vij为i作业单元与j作业单元之间物料搬运速度。当i=j时，Pij、Fij、Vij=0。

采用归一化因子u1、u2来统一量纲[9]，u1、u2的计算如式（3）、式（4）所示。考虑到实际生产中对多个优化目标的侧重不同，加入加权因子w1、w2，且满足w1+w2=1(w1、w2∈(0,1))，最终得到目标函数表达式如式（5）所示。

式中：G为加权后的目标函数值；Dmax为两作业单元间可能存在的最大曼哈顿距离，近似为车间的长和宽之和；v′ij为车间所有路径上物料搬运速度的平均值。

1.3 约束条件

在对车间不同作业单元的布局进行建模优化时，还需要结合实际情况建立约束条件，主要包括以下内容。

（1）间距约束。不同作业单元之间需要保持一定的距离，即

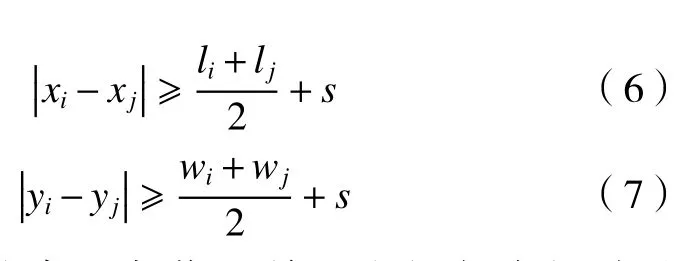
（2）通道约束。各作业单元之间与车间墙壁之间需要保留一定的距离，即

（3）尺寸约束。同一行或同一列的所有作业单元在在X轴或Y轴方向上的布局不得超过车间的长度或宽度，即

式中：s为 最小间距。

2 自适应遗传模拟退火算法

为了对上述模型进行求解，提出一种自适应遗传模拟退火算法，即在传统遗传算法上对交叉变异算子采用自适应调整策略；同时利用模拟退火算法的概率突跳性来降低过早收敛的可能性，进一步增强算法求解性能并基于Metropolis准则判断是否接受新个体。算法流程如图2所示。

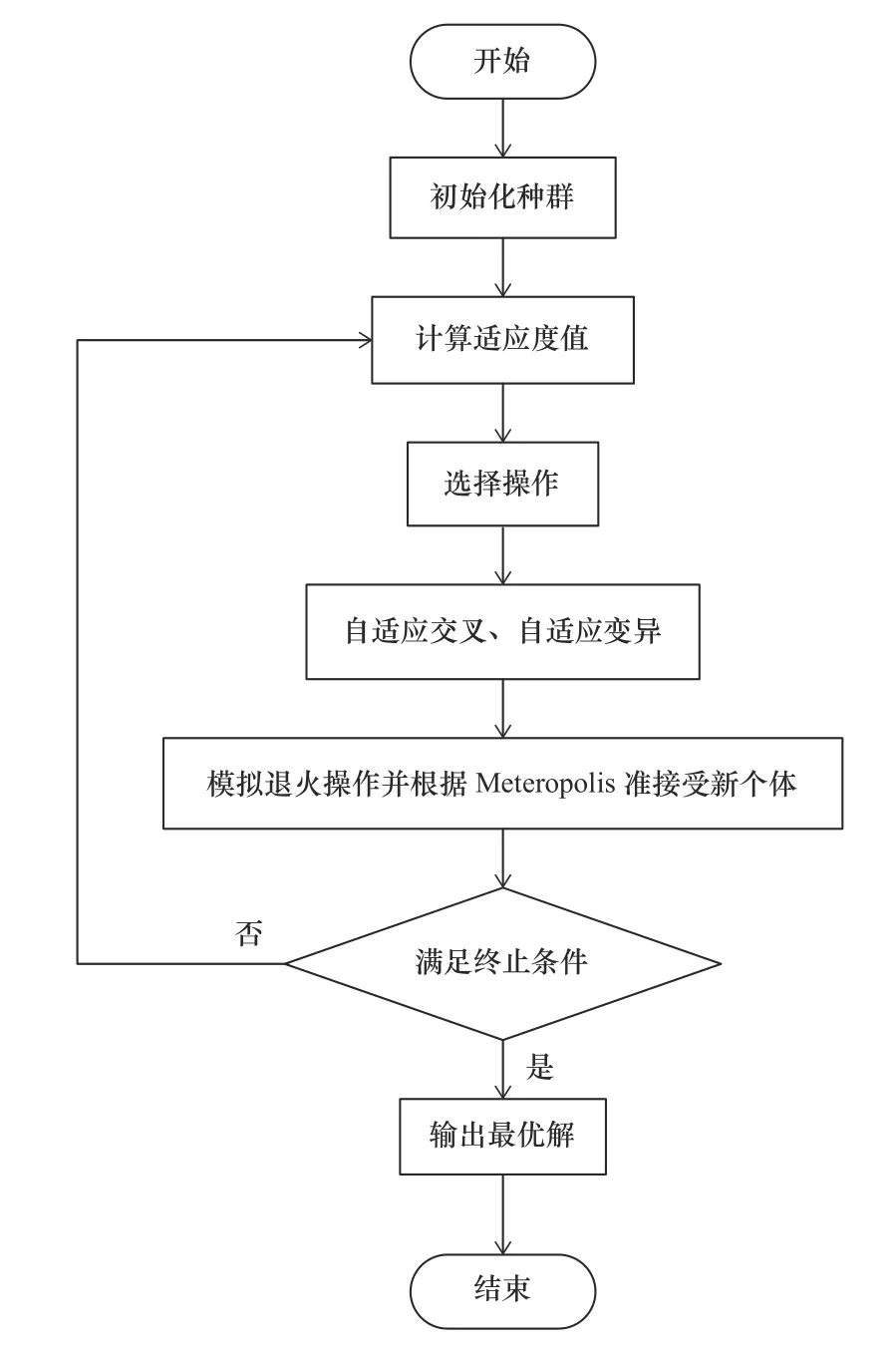
图2 算法计算流程

2.1 种群初始化

本文采用实数编码的方式构建个体的基因序列，编码样式为[m1,m2,m3,m4,···,mN]，代表的含义是自车间区域自左下角依次沿X轴正方向布置作业单元，当布置的作业单元总长度超出车间长度时，沿Y轴正方向另起一行，从最左端继续向右依次布置，例如个体编码[2,7,3,10,1,4,5,···]的布局即图3所示。

图3 编码示例对应的车间布局图

2.2 适应度函数

本文中综合优化目标是求最小值，设置适应度函数fi为

式中：G为目标函数；P为惩罚函数。惩罚函数定义为

2.3 选择算子

为保证种群基因多样性并且同时提高算法的收敛效率，本文选择轮盘赌加部分精英保留的策略进行选择操作。轮盘赌策略中，个体i被选中的概率Pi为

式中：popsize为种群大小；fi为第i个个体的适应度值。

采用轮盘赌的方式选出下一代种群中一半的个体后，采用部分精英保留策略选出另一半的个体，选出的所有个体组合成子代种群。

2.4 交叉算子

由于车间布局问题中个体基因型的代码具有特殊含义，因此本文采用基于位置的交叉算子，其具体操作如图4所示。

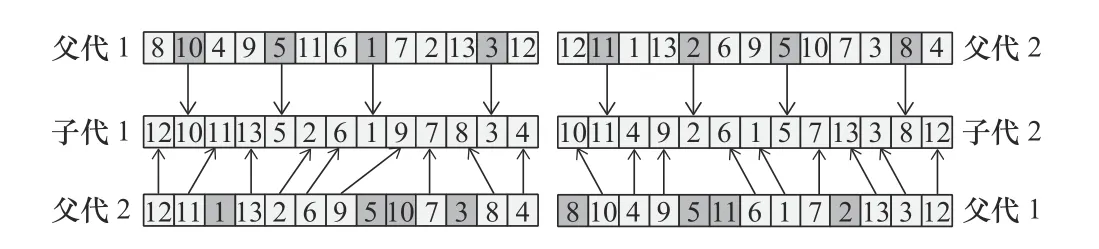
图4 交叉过程

2.5 变异操作

在实数编码下，基因序列上的每一个数字都具有特殊的含义，无法采用二进制编码下的各种变异方法。针对本问题，为了保证变异之后的个体仍具有意义，采用互换变异的方式进行操作，如图5所示。

图5 变异过程

2.6 自适应交叉、变异策略

遗传算法中，交叉概率Pc和变异概率Pm是影响算法寻优能力的重要参数，由于自适应取值法对交叉、变异算子进行非线性设计，使得交叉概率与变异概率随种群中个体的适应度值的变化而变化，能够防止算法陷入过早收敛[10]，因此本文对Pc、Pm的取值采用自适应取值法，取值计算过程如式（15）、式（16）所示。

式中：Pcmax与Pcmin分别为遗传操作过程中交叉概率取值区间的上、下限，f′为进行交叉操作两个个体中较大者的适应度值，favg为每代种群的平均适应度值，fmax为当前种群中的最大适应度值，λ为常数。

式中：Pmmax、Pmmin为变异概率取值区间的上、下限，f为变异个体的适应度值，favg为每代种群的平均适应度值，fmax为当前种群中的最大适应度值。

2.7 嵌入模拟退火算法

在遗传算法中嵌入模拟退火算法，借用模拟退火算法的概率突跳性增强算法全局寻优的能力。设定初始温度t作为模拟退火寻优的起始点，设定终止温度Tend作为模拟退火寻优的终止点，在等温状态下交换个体前后一半基因并依据Metropolis准则计算新个体被接受的概率，其计算公式如下

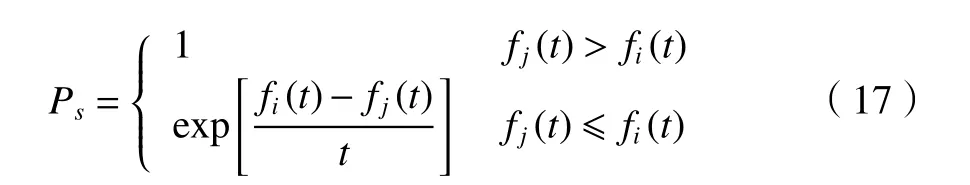
式中：Ps为新个体接受的概率；fi(t)为个体变换前的适应度值；fj(t)为个体变化后的适应度值；t为当前温度。依据式（14）更新当前温度，即

式中：λ为温度衰减参数，用于控制退火速度，且取值大小满足λ∈(0，1)。

3 计算实例

3.1 车间概述

FK公司是一家主要从事汽车零部件设计和制造的公司，该公司生产车间为30 m×25 m的矩形，车间内有11套各式加工机床以及原材料、成品存放区。为方便描述，用序号表示各作业单元，各作业单元的尺寸数据见表1，车间的原始布局如图6所示。

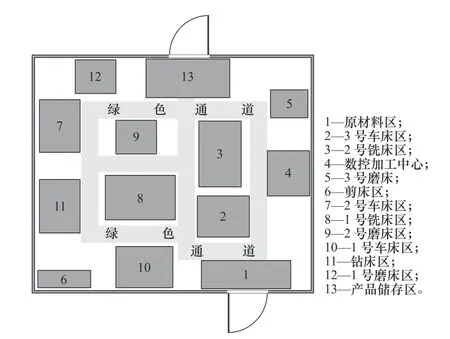
图6 车间原始布局

根据产品的工艺流程以及不同作业单元间物料搬运方式的差异，作业单元间的单位费用如表2所示，作业单元间的搬运频率如表3所示，作业单元间的搬运速度如表4所示。

3.2 优化过程及相关参数设定

设定最小间隔参数s为1 m。由表2、表3、表4的数据，计算出归一化因子u1=4.905×10−6、u2=5.646×10−5。根据对优化目标的侧重不同，设定权重因子w1=0.6，w2=0.4。种群数量设定为50，迭代次数gen为500代，保证算法充分进行寻优搜索。为验证不同算法的设计以及不同参数的选取对算法寻优的影响，引入4种不同的方案进行对比，具体如表5所示。

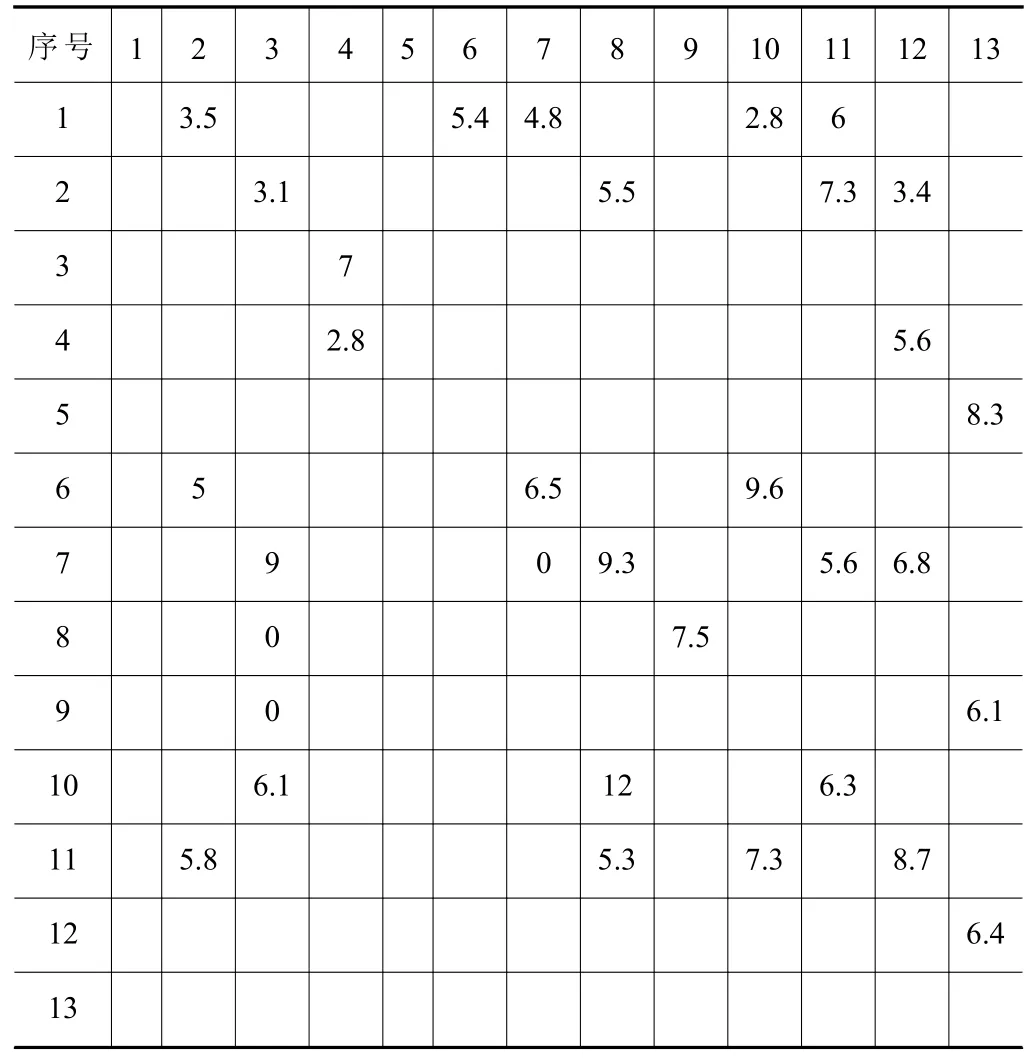
表2 作业单元间的单位费用 元/m

表3 作业单元间的搬运频率 次/天

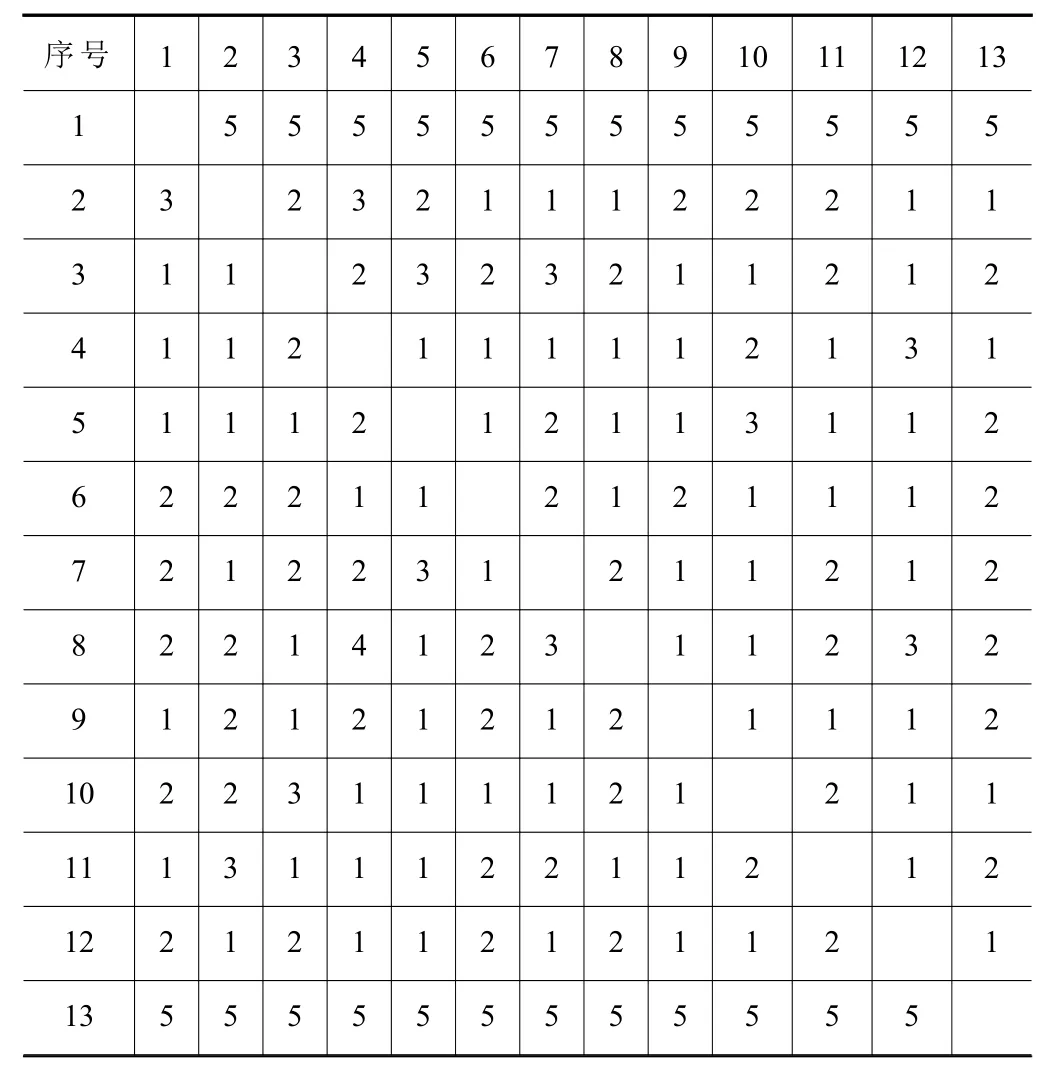
表4 作业单元间的搬运速度 m/s

表5 算法参数设定对比

3.3 优化结果及分析

在MATLAB软件上运行各套算法对车间布局问题进行求解，运行结果如图7所示。从图7可以看出，各算法在迭代一定代数之后停止了波动，达到收敛。经计算，方案1至方案3求解得到的最优目标函数值分别为0.180、0.175、0.169，本文提出的自适应的遗传模拟退火算法求解得到的最优目标函数值为0.158，比普通遗传算法寻优结果更优秀，由本文算法求解得到的最优个体为[5,13,10,1,11,4,3,6,2,8,9,7,12]，其车间作业单元布局如图8所示，各作业单元的位置坐标如表6所示。

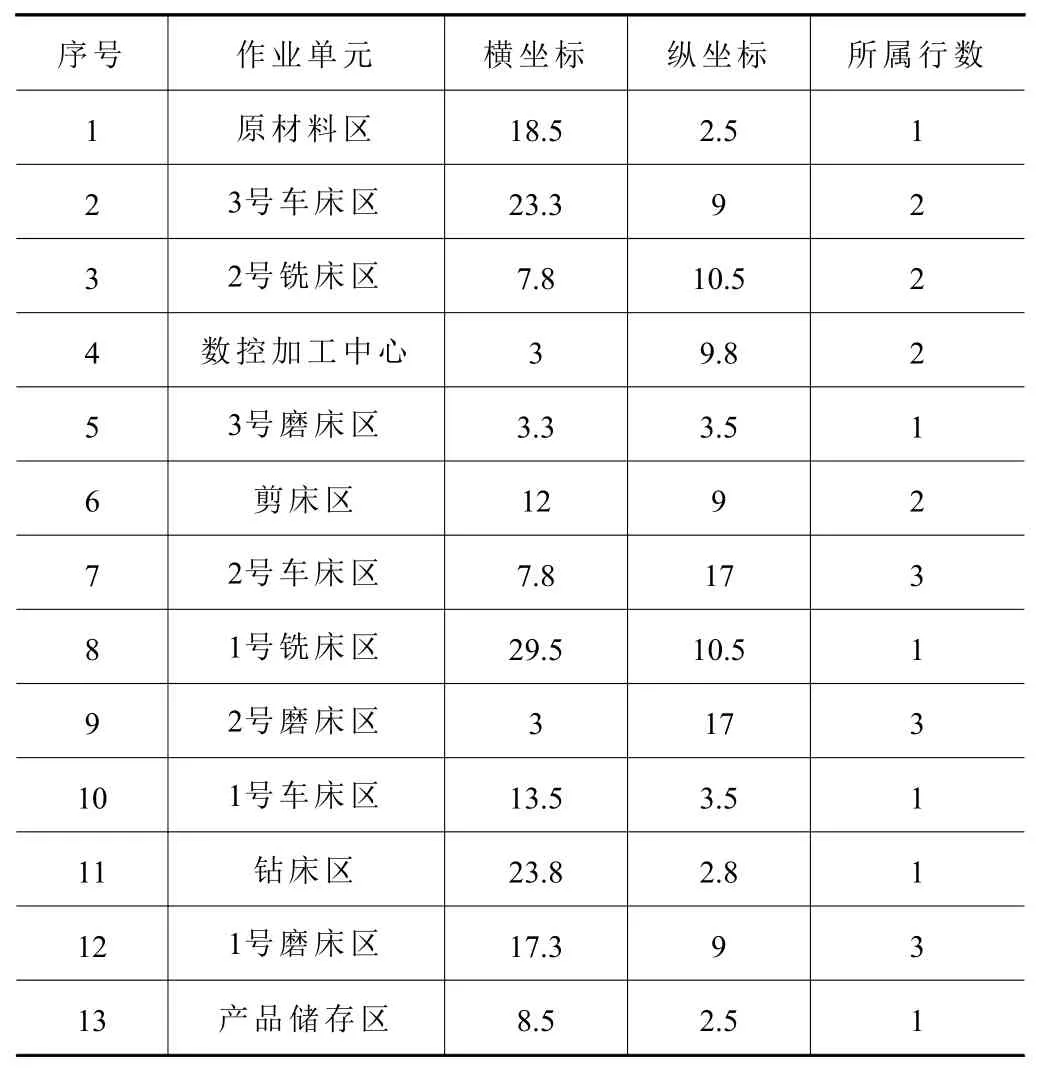
表6 优化后作业单元位置坐标

图7 算法优化过程迭代图

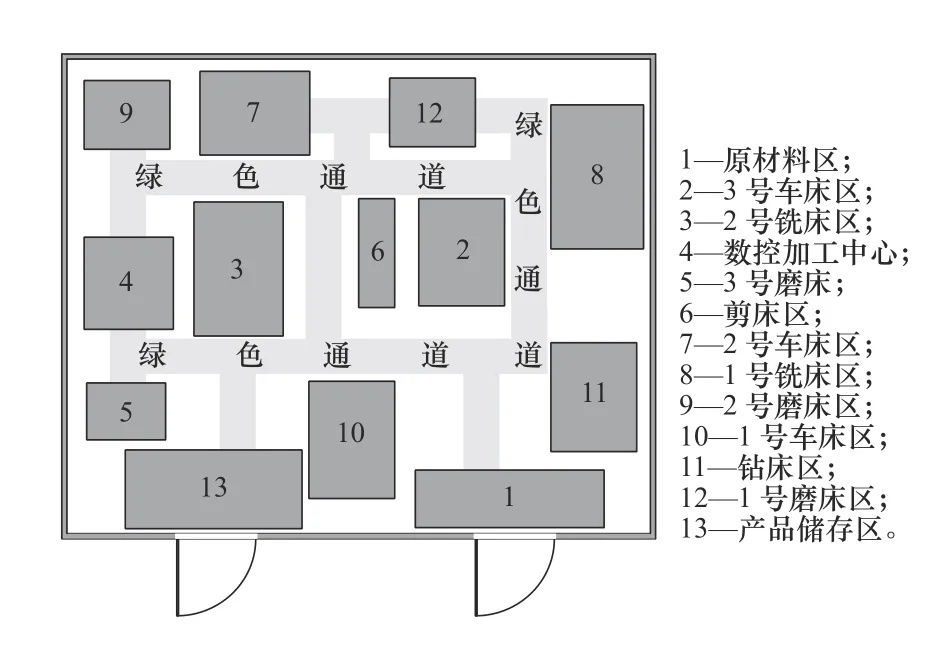
图8 优化后车间作业单元布局

为了评估优化效果，将原布局与优化后的布局下的搬运费用及搬运时间进行对比，如表7所示，对比发现优化效果显著。

表7 优化前后对比

4 结语

针对车间设施布局优化问题，本文以最低车间物流成本与最短车间搬运时间为优化目标建立数学模型，采用自适应遗传模拟退火算法对问题进行求解，并通过4种参数设定方案对比验证了自适应策略的算法的优越性。给出了FK公司的车间设施布局优化案例，结果表明，经遗传模拟退火算法优化后得到的车间布局方案，相较于原始布局方案，其车间物流成本降低了9.98%，车间搬运时间缩短了20.8%，证明该算法有较强的寻优能力，可以为企业车间生产制造减少浪费，提高效率。

在后续工作中，还需要继续结合其他算法的思路对算法进行改进，同时车间布局数学模型的复杂度需结合实际情况作进一步的完善。