齿面硬化层对重载齿轮力学性能的影响研究

沈益晨 陈启东

（①苏州大学机电工程学院，江苏 苏州 215000；②常熟理工学院机械工程学院，江苏 常熟 215500）

重载齿轮是传递运动和动力的传动系统核心关键零件，在矿山机械、航空航天和新能源等行业有着广泛的应用，因此，对其服役性能和疲劳寿命也提出了很高甚至是苛刻的要求。在齿轮的生产过程中，经常会通过渗碳、渗氮、喷丸以及涂敷涂层等工艺对齿轮进行表面硬化处理来提高整体性能，延长使用寿命。王克胜[1]等从有效硬化层深度的定义出发，得出了有效硬化层深度的最小值和最大值分别由接触强度和弯曲强度决定的结论。丰瑞华[2]等建立了渐开线齿轮进行激光淬火时的三维温度场数值模型并进行模拟，获得了与试验一致的结果。郁俐[3]等研究了强力喷丸对18CrNiMo7-6钢不同硬化层深度齿轮性能的影响。Tobie T[4]等研究了渗碳深度对渗碳齿轮点蚀强度和弯曲强度的影响，得出在不同工作条件下的最佳渗碳深度。Moorthy V[5]等评估不同涂层下斜齿轮的性能，研究认为，Nb-S涂层齿轮的整体接触疲劳性能最好。Karthick S[6]等研究了通过使用喷丸强化工艺来提高 SAE9310锥齿轮的机械和表面性能，以获得所需的性能特征和对表面层特征的最大影响因素。

可见，国内外学者对齿轮表面硬化技术已经做了很多研究，然而，这些研究大多集中在工艺参数对表面硬化结果产生的影响。对于齿面硬化层中硬度的梯度分布研究较少，传统的计算方法无法准确地得到齿轮在不同硬化深度下的应力分布及变化规律。本文利用多层均质层代替硬化部分，以某型号采煤机重载齿轮为对象，建立更切合实际的硬化齿轮有限元模型，考虑不同的硬度梯度分布、不同的硬化层厚度下齿轮产生的应力分布，研究齿面硬化层对重载齿轮力学性能的影响，对准确分析表面硬化齿轮的强度及表面加强工艺具有重要的理论和指导意义。

1 模型建立及验证

1.1 赫兹接触基本理论

齿轮接触强度问题普遍以赫兹接触理论作为理论基础。两个圆柱体的轴线相互平行，其弹性模量分别为E1、E2，泊松比分别为μ1、μ2，半径分别为r1、r2，由单位长度上的力F压紧，此时，在平行于轴线，宽度为 2a的区域形成接触，由于圆柱体长度为单位长度，模型可简化为二维接触模型，如图1所示。根据赫兹接触理论可知最大接触应力P，其表达式为

图1 赫兹接触模型

式中：a为接触半径，；E∗为等效弹性模量，；r为综合曲率半径，。

最大剪应力τ为：

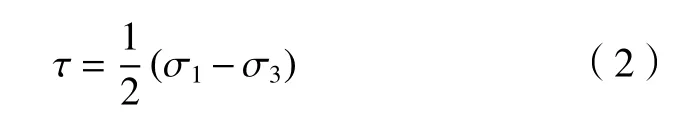
式中：σ1、σ3分别为主应力的最大值和最小值。

1.2 硬化层模型建立方法

齿轮硬度梯度的合理建模是本研究的关键，建立准确的硬化层模型对于问题的分析与研究才有实际意义。因此，本研究提出一种用多层均质层来替代齿轮硬化层的建模方法，利用双三次B样条曲面理论[7]获得齿廓曲面，以该齿廓面为基面，沿点阵的负法向方向进行等距偏置，再以等距偏移面为基础向内偏移，以此往复，得到组成齿轮硬化部分的各均质层。

圆柱齿轮的齿廓由渐开线曲线、齿根过渡曲线、齿顶圆弧和齿根圆弧组成。渐开线曲线方程为

式中：xd、yd分别为曲线上点的横、纵坐标；rb为基圆半径；λ=tanα，α为压力角。

齿根过渡曲线是在齿轮加工过程中由刀尖的圆角形成的。加工刀具和加工方法可以改变齿根过渡曲线。本研究采用滚齿法加工的齿轮，齿根过渡曲线是渐开线延伸的等距曲线。齿根过渡曲线的参数方程为

齿顶圆弧与齿根圆弧的方程分别为

即齿顶圆弧与齿根圆弧横坐标分别等于齿顶与齿根圆弧半径。

通过齿廓曲线方程可以获得一系列的齿廓点，根据曲率大小自适应调整齿廓上取点的密度，以保证造型的精度。在完全获得齿廓点后，沿轴线方向阵列若干层，得到齿廓面的点矩阵Ai, j。双三次B样条曲线方程为

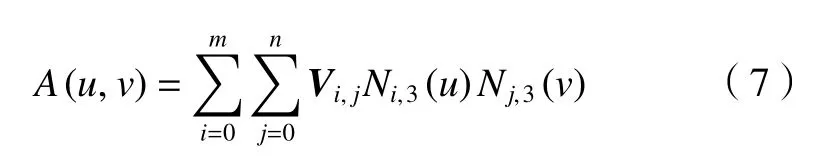
式中：Vi, j（i=0,1,···,m；j=0,1,···,n）为曲面控制点矩阵；Ni,3（u）和Nj,3（v）分别为分别为沿u和v方向的3次B样条基函数。

通过式（6）可以计算出曲面上每一点u和v方向的切向量。每一点上的法向量是两个切向量的叉积，再除以交叉模的大小得到单位法向量n。将该点沿单位法向量反向偏移ti距离即可得到该点的法向偏移点，表达式如下。

将齿廓点阵沿法线方向偏移t1距离，得到偏移点阵并进行拟合，得到第一个等距偏移曲面，该曲面与齿廓曲面顺次连接形成第一层硬化层。以第一个偏移曲面为基面，继续向内建立等距偏移曲，形成第二层均质硬化层，重复上述操作，最终可以得到其余硬化层。

1.3 齿轮有限元建模及验证

以某采煤机减速器一对渐开线直齿轮为研究对象，其相关参数如表1所示。通过上述方法获取齿廓线的点矩阵，并根据点的坐标序列生成igs文件。然后，将文件导入通用建模软件，通过拟合点矩阵得到齿廓面。利用外部编程成功地得到了等距偏移曲面。将生成的等距偏移曲面的igs文件导入到ABAQUS中，利用由面生成体的命令得到硬化层实体模型。最后通过阵列以及布尔运算等操作构建出齿轮模型。

表1 减速器齿轮参数

考虑到齿轮是高度对称部件，因此为节省计算量及时间，取1/4进行分析，图2所示为将硬化层分为3层的主动轮。齿轮基体材料选取采煤机齿轮常用的17CrNiMo6[8]，弹性模量E=210 000 MPa，泊松比υ=0.3；最外层弹性模量E'=220 000 MPa，泊松比υ'=0.3。硬化层组元成分分布采用Wakashima K等[9]提出的幂函数形式渐变，沿齿轮径向方向上分布为

图2 主动轮示意图

式中：V(h)为最外层材料在硬化层中的体积分数；h为沿着齿轮厚度方向硬化层厚度；δ为硬化层的总厚度；p为成分分布指数；通过改变p值的大小，可以改变硬度梯度分布形式。

本算例网格类型为四边形一阶非协调单元，对主要受力的轮齿部分进行加密，如图3所示；以小齿轮为主动轮，大齿轮为从动轮，首先将齿轮内圈与各自的中心进行耦合，然后对主动轮中心施加大小为16 000 N·m的转矩，分别释放主、从动轮绕轴线的旋转自由度，约束住其余所有自由度，如图4所示。由于齿轮在啮合过程中表面既存在滚动又存在滑动[10]，此接触类型设置为Frictional，摩擦系数设置为0.1。

图3 齿轮网格模型

图4 齿轮装配图

将模型提交运算，选取一对轮齿具有代表性的6个增量步为例，计算结果如图5所示。由应力云图可知，齿轮啮合过程中，应力分布以接触点为中心，呈现均匀散射状，轮齿的齿顶、齿根及接触齿面所受应力较大，且接触点中心处产生最大接触应力，其中最大接触应力为952 MPa。由式（1）计算可得赫兹接触理论强度为927 MPa，有限元计算结果与理论公式计算结果相比，误差小于3%，这表明有限元模型计算精度高，能够准确模拟后续不同硬化层齿轮的应力场分析。

图5 应力云图

2 力学性能分析

2.1 有无硬化层对应力的影响

传统的齿轮应力分析，将硬化层视作与基体相一致的材料，本文提取啮合线上均匀分布的10个接触点作为研究对象，近似得到单个轮齿在一个啮合周期内的接触应力变化规律，比较两种建模方法的应力大小。图6为有无硬化层的接触应力情况。由图可知，两种模拟方法的接触应力发展趋势相似，啮合过程中接触应力值先呈现上升趋势，然后在接触点5和6之间应力达到峰值，最后应力值逐渐减小。在对硬化层进行分层处理后，接触应力值整体有所下降，并且应力值变化整体趋于平缓，在接触中心附近，应力峰值从1 013 MPa降低到952 MPa。通过与理论计算值比较，有限元仿真的结果整体大于理论值，这是因为理论计算只考虑对称循环应力最大值作为最大应力值，忽略了脉动循环应力，而利用有限元方法读取结果时，根据的是第三强度理论，读取表面最大应力。同时，设置硬化层的计算值更接近理论值，说明该建模方法更接近实际，具有一定科学性。

图6 有无硬化层接触应力对比

2.2 硬化层硬度梯度形式对应力的影响

建立2 mm厚的硬化层，依次改变硬化梯度分布形式指数p，研究不同硬化层梯度形式对齿轮应力场的影响。图7所示为不同硬度梯度下的最大接触应力值及产生位置。由图可知，最大接触应力值随着硬化层分布指数的增大逐渐减小，减小趋势趋于平缓，表明硬化层分布指数对最大接触应力值的影响越来越小；当分布指数p小于1时，最大接触应力发生位置变化不大，发生在表层，随着硬化层分布指数增大，最大接触应力位置迅速下移，当p=4时，最大接触应力已经离开硬化层进入基体。

图7 硬化层分布指数对接触应力的影响

图8为硬化层分布对剪应力分布的影响，横坐标l/a表示与接触点的距离。由图可知，剪切应力随着l/a的增大而增大，最大值出现在接触半宽附近；在l/a=1附近剪切应力有一个突变，随后逐渐减小。剪切应力随硬化层分布指数的增加有所变化，且变化影响较大。当分布指数p为0.25～1时，接触半宽附近的剪切应力逐渐减小，当分布指数p为1～4时，接触半宽附近的剪切应力又开始增大。

图8 硬化层分布指数对剪切应力的影响

2.3 硬化层厚度对应力的影响

将模型硬化层层厚度依次设置为0.5 mm、1 mm、1.5 mm、2 mm，研究不同硬化层厚度对齿轮应力场的影响。图9所示为不同厚度下的最大接触应力值及产生位置。由图可知，不同厚度的硬化层对接触应力影响较大，随着硬化层厚度增加，最大接触应力先减小后增大，硬化层厚度为1 mm时，接触应力最小。硬化层厚度过小或过大时，均产生较大接触应力且变化幅度陡峭；随着硬化层厚度增加，最大接触应力发生位置开始下移，与齿面距离逐渐增大，当硬化层厚度在0.6 mm左右时，最大接触应力进入到硬化层，当厚度达到1.5时，最大接触应力位置开始迅速向齿根方向移动。

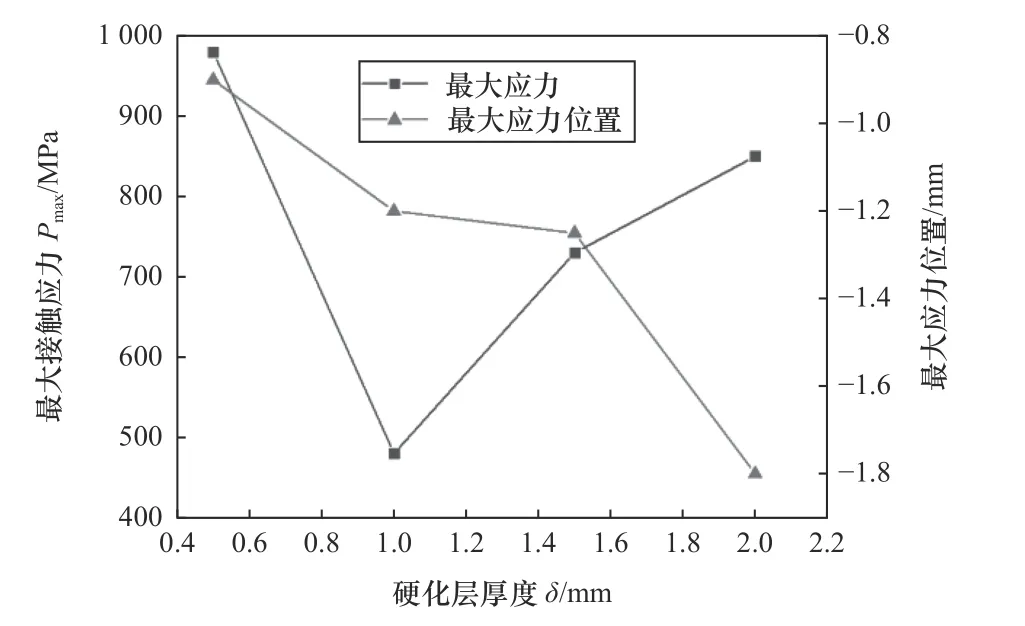
图9 硬化层厚度对接触应力的影响

图10为硬化层厚度对剪应力分布的影响。由图可知，最大剪应力出现在l/a=1处，即接触半宽的位置并且随后迅速减小直至趋于零；随着硬化层厚度增加，剪应力明显减小且变化更加平缓，表明硬化层厚度对界面影响较大，厚度的适当提高可以缓解齿面磨损剥落。

图10 硬化层厚度对剪切应力的影响

3 结语

通过建立某型号含梯度硬化层齿轮的有限元模型，对采煤机重载工况下齿轮的受力情况进行分析，探究了硬化层梯度分布形式、硬化层厚度等因素对采煤机重载齿轮力学性能的影响，得到以下结论：

（1）本文提出的表面硬化齿轮建模方法对其进行啮合性能仿真结果更加接近于实际情况，具有一定的科学性。

（2）硬化层分布指数的增大能有效减小接触应力，分布指数过大，最大接触应力将发生在齿轮基体，分布指数p=1时，剪切应力最小，提高了齿轮使用性能，延长使用寿命。

（3）硬化层厚度对最大接触应力影响较大，剪切应力随硬化层厚度的增加而增大。综合考虑应力及界面结合强度，硬化层厚度应当控制在1～1.5 mm。