带肩衬套冷缩装配孔径收缩量仿真与试验研究

袁 田 李小兵 陈保林 张安顺 张 利

（航空工业成都飞机工业（集团）有限责任公司，四川 成都 610092）

在飞机组件上存在大量可动连接，带肩衬套与组件采用过盈配合的方式实现力和扭矩的传递，目前常用的过盈装配方法主要有冷挤压装配法和冷缩装配法[1]。冷挤压装配方法直接采用外力将带肩衬套压入基座中，在装配过程中，基座孔壁在外力作用下会对带肩衬套外圆柱面进行“挤压光整”加工，使带肩衬套外圆柱面出现鱼鳞状拉伤，基座配合面也会出现毛刺甚至被切削掉，从而造成实际过盈量小于理论过盈量，进而降低衬套机械性能[2]。冷缩装配方法是通过液氮介质对带肩衬套进行深冷处理，然后迅速装入基座中，待带肩衬套恢复至常温，两者便牢固地装配在一起，但在带肩衬套外圆柱面与基座孔壁配合面之间存在挤压力p，相对于刚性较好的基座来说，在挤压力p的作用下，带肩衬套会产生收缩变形，后续需对内孔进行二次补充加工，因此研究分析冷缩装配过盈量与装配后衬套内径收缩量之间的关系，修正带肩衬套孔径加工尺寸公差带，对于提高组件装配效率、降低补充加工风险有着极为重要的意义[3−4]。

在冷缩装配工艺过程中，过盈量太小会导致衬套脱落，过盈量太大又会引起装配变形等问题，因此过盈量的设计一直是过盈装配理论研究中的核心内容之一。姚秦秋[5]基于装配实践最早发现在基座与衬套材料物理性能相近的情况下，其衬套收缩值Δ总是大于过盈量值δ，并通过相关性试验获得了在相同材料下，衬套内径公差带正向调整经验公式。随后，许德明[6]提出了冷缩装配后衬套孔径收缩量的变化规律，并指出冷装衬套内径收缩量的大小与实际过盈量、衬套及基座的厚薄，衬套、基座的材料有关。冯伟[7]基于材料力学理论研究了衬套装配前后应力与应变，并提出在过盈量较小的情况下，简单衬套内径收缩量计算公式。滕淑珍[8]针对常用的钢、铜两种材料衬套冷缩装配过程进行了研究，并基于第三、第四强度理论，给出了衬套过盈量、收缩量计算公式及强度校核方法。

随着有限元软件的飞速发展与迅速普及，对衬套类零件过盈装配过程的接触问题的研究越来越深入，范校尉[9]在厚壁圆筒过盈装配理论的研究基础上，使用ANSYS分析了连杆衬套与连杆小头端过盈装配过程，验证了仿真值与理论值一致性。梁大珍[10]、乔文元[11]等通过Workbench有限元仿真，给出了不同过盈量下衬套应力分布以及最大应力与过盈量之间的关系。方焱[12]使用ABAQUS有限元软件，结合ABAQUS有限元仿真和试验的方法，验证了衬套外径冷缩量分别与衬套材料的热胀系数和衬套外径大小成正比，装配过盈量对装配后衬套内径收缩量具有显著影响。

近年来，虽然各行各业的学者在过盈配合的理论研究、有限元仿真模拟及其工程化应用方面，均取得了较多的研究成果，但是大都针对普通光头衬套，对于带肩衬套尚缺少分析，鉴于带肩衬套冷缩装配在飞机组件装配中占比较大，因此有必要对带肩衬套从有限元仿真分析和试验两方面进行深入研究，进而指导带肩衬套冷缩装配过程。

1 φ64 mm带肩衬套冷缩装配变形分析

1.1 仿真模型建立

采用ABAQUS 有限元软件进行仿真分析，作为国际先进的大型通用有限元软件之一，具有极强的非线性能力，可以直接使用软件内置的接触算法模拟整个带肩衬套冷缩装配过盈配合过程。在进行有限元分析时，由于实际带肩衬套和安装基座都为回转体结构，为了减小仿真计算量，本次对带肩衬套和基座进行了合理简化，采用实际模型的1/2作为仿真模型，利用ABAQUS中Part模块进行带肩衬套和基座模型的建立，带肩衬套外径为φ64 mm，内径为φ58 mm，高度28 mm，基座内径为φ64 mm，外径为φ90 mm，高度37 mm，带肩衬套和基座材料分别为Al7050和Cr16Ni6，仿真三维模型如图1所示。

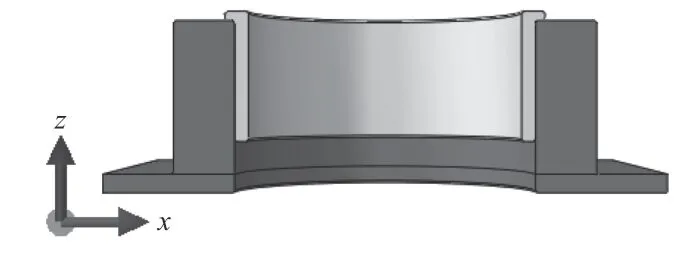
图1 仿真三维模型

带肩衬套冷缩装配有限元分析设置两个分析步：Step1，带肩衬套低温冷却过程；Step2，衬套从液氮深冷处理后温度−196 ℃恢复至室温20 ℃过程中受热膨胀，并与基座发生接触挤压发生变形，分析步类型选择“温度–位移耦合分析”，在带肩衬套外圆柱面与基座内孔之间设置相应过盈量以及环境温度，模拟衬套冷缩、膨胀的过程。

1.2 仿真结果分析

图2所示为带肩衬套冷缩装配不同过盈量下带肩衬套内径收缩量变形云图。由变形云图可以看出，不同过盈量下，带肩衬套最大收缩量是不同的，当带肩衬套与基座间过盈量为0.043 mm时恢复室温后，带肩衬套内径最大收缩量为0.033 5 mm，随着过盈量的增大，带肩衬套内径最大收缩量也增大，当带肩衬套与基座间过盈量为0.084 mm时，带肩衬套内径最大收缩量为0.063 3 mm。并且可以看出带肩衬套在冷缩装配恢复室温后沿Z+方向带肩衬套内径收缩量逐渐变小，表明衬肩结构加强了靠近衬肩部位的刚度，使得靠近衬肩部位在恢复室温过程中，受到基座相同的挤压压强下，内径收缩量较小。对φ64 mm带肩衬套进行冷缩装配试验，将带肩衬套试验件放入液氮进行深冷处理0.5 h后，迅速装入试验基座中，恢复室温24 h后，测量带肩衬套内径最大收缩量如图3所示，冷缩装配试验和仿真获得的最大收缩量如表1所示，以带肩衬套与基座装配过盈量为横坐标，带肩衬套内径最大收缩量为纵坐标，得到过盈量与衬套内径最大收缩量的关系。

表1 带肩衬套内径最大收缩量

图2 不同过盈量下的带肩衬套冷缩装配有限元仿真云图

图3 φ64 mm带肩衬套及测量过程

从图4可知，随着带肩衬套与基座之间过盈量的增大，带肩衬套最大收缩量也线性增大。仿真分析得到的带肩衬套收缩量与冷缩装配试验收缩量存在一定的差异：一方面是由于冷缩装配试验通过人工手动使用内径三爪千分尺进行测量，即使在测量位置做好标记并且进行多次测量以减小误差，但每次不能保证在带肩衬套收缩量最大的位置进行数据测量，而且带肩衬套在轴向方向上，内径收缩量相对测量位置较为敏感，在远离衬肩的位置，较小的距离，会引起衬套内径收缩量较大的变化；另一方面，在冷缩装配过程中，由于带肩衬套多为薄壁件，加工后的圆度以及圆柱度都难以得到保证，所以实际加工出来的带肩衬套可视为“椭形”，对于基座来说，一般采用精度更高的镗孔加工工艺，因此可将基座内孔视为“圆形”，对于“椭形”与“圆形”之间的配合，总是与仿真搭建的环境模型存在一定的偏差。但有限元仿真分析获得的内径最大收缩量相对于冷缩装配试验得到数据误差低于9%，说明仿真搭建的环境模型能够较好地模拟带肩衬套冷缩装配过程，可以用于后续不同型号带肩衬套冷缩装配内径收缩量分析研究。

图4 过盈量与衬套内径最大收缩量的关系

2 φ34 mm带肩衬套冷缩装配内径收缩量计算

2.1 带肩衬套装配应力、变形公式

根据材料力学厚壁圆筒过盈装配理论[13]，装配压力p作用在衬套外圆柱面，衬套外径的收缩量为δi；对于基座来说，装配压力p作用在基座内圆柱面，基座内径伸长量δe。

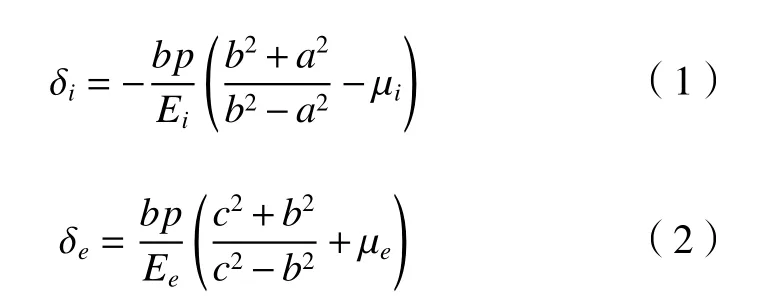
由图5可以看出，理论过盈量 δ为

图5 过盈装配示意图

将式（1）、（2）代入式（3）整理可得

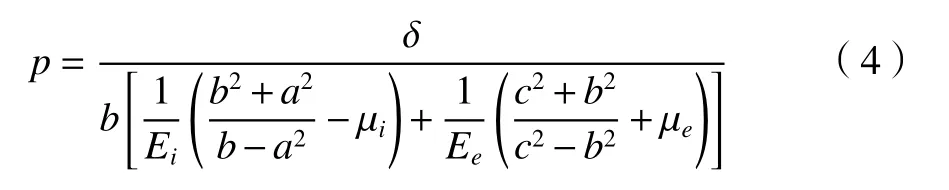
式中：Ei和µi分别为衬套材料的弹性模量和泊松比，Ee和µe分别为基座材料的弹性模量和泊松比，由于衬套存在衬肩结构，需要对装配压强进行修正，修正后装配压强p′为

式中：η为修正系数，与带肩衬套结构有关。

式（1）为衬套外径收缩量，由于金属密度随温度变化不大，可认为带肩衬套装配前后横截面积保持不变，求得内径收缩量δa为

整理可得

式中：δb=δi为带肩衬套外径收缩量，由于相较于b来说很小，可以忽略不计，整理可得带肩衬套内径收缩量。

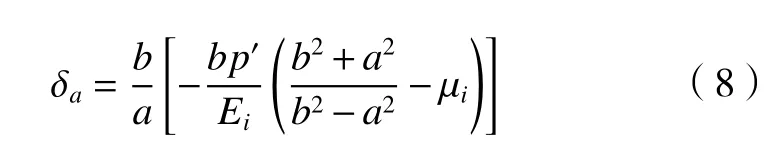
2.2 基于仿真试验获取衬套收缩量经验公式

通过对φ64 mm带肩衬套冷缩装配变形分析，得到准确的仿真环境，下面对φ34 mm带肩衬套进一步研究，以获得该型号带肩衬套收缩量经验公式，φ34 mm带肩衬套外径尺寸设计模型公差分布在+0.043～+0.088 mm，基座安装孔内径尺寸设计模型公差分布在+0.019～+0.039 mm，分析可知带肩衬套与基座装配最大过盈量为+0.069 mm，最小过盈量为+0.004 mm，进而对φ34 mm带肩衬套进行了16组不同过盈量仿真分析，仿真预设过盈量最大值0.069 mm，最小值为0.009 mm，步长0.004 mm，仿真结果如表2所示。

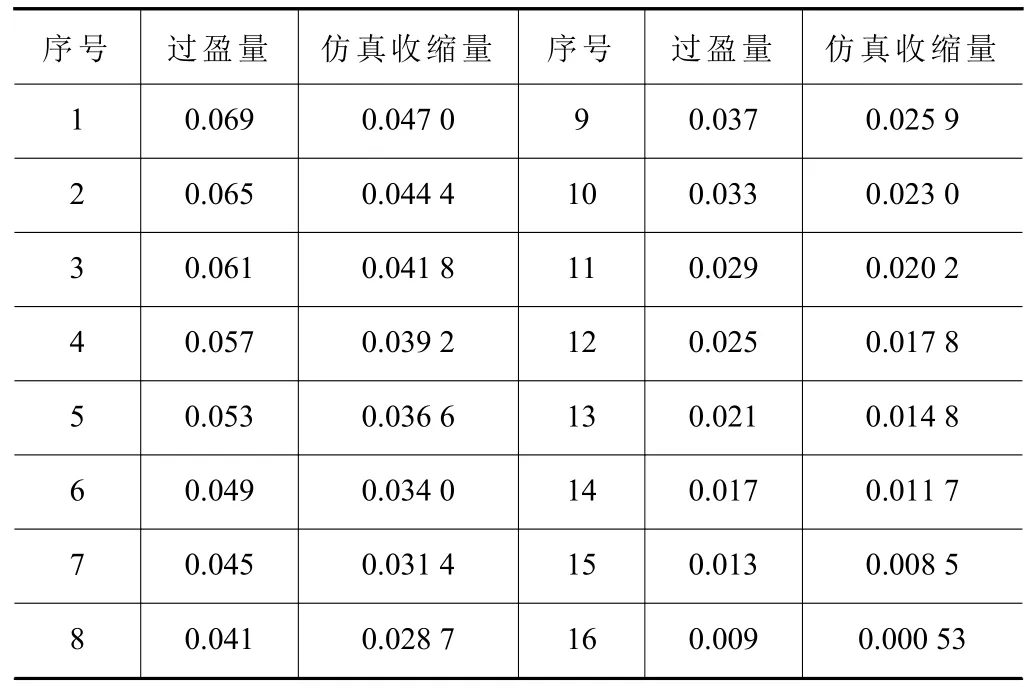
表2 有限元分析获得的仿真收缩量mm

提取φ34 mm带肩衬套仿真结果，以预设过盈量为横坐标，仿真变形量为纵坐标，获得预设过盈量与仿真变形量曲线图，如图6所示，虽然带肩衬套受到衬肩加强结构的影响，但是随着过盈量的增加，带肩衬套内径最大收缩量也增大，由式（8）可知内径收缩量与理论过盈量变化趋势呈线性关系，通过Origin软件对仿真收缩量与预设过盈量进行线性拟合分析获得回归方程

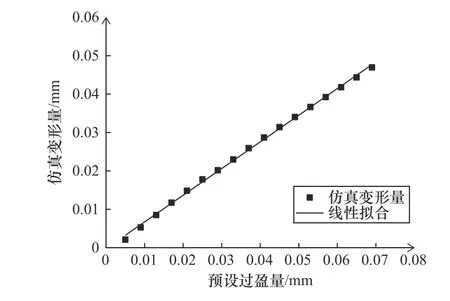
图6 预设过盈量与仿真变形量关系曲线

式中：δa为带肩衬套内径最大收缩量；δ为理论过盈量，回归拟合R平方（COD）相关系数为0.998 59，残差平方和为8.132×10−6，说明数据相关度较高，拟合程度良好，可以用于计算φ34 mm带肩衬套在不同过盈量下内径收缩量。

2.3 带肩衬套冷缩装配应用

在相同的试验条件下，对φ34 mm带肩衬套进行冷缩装配，恢复室温24 h后测量带肩衬套内径最大收缩量，并将试验得到的过盈量代入回归方程（9）中，计算获得带肩衬套内径收缩量，并与试验最大收缩量进行对比分析，冷缩装配试验过程如图7所示，数据如表3所示。从表3可以看出，试验结果与仿真值较为符合，分析误差主要源于以下两个方面。

表3 试验值与计算值对比分析

图7 冷缩装配试验过程

（1）测量仪器的测量精度、结构对测量结果的影响。一方面，冷缩装配试验所使用的测量仪器精度为±0.001 mm的电子内径三爪千分尺，在测量直径较小的带肩衬套时相对误差更大；另一方面，由于测量爪存在特定的尺寸特征，而且两种型号带肩衬套高度不同，φ34 mm测量接触位置误差更大，并不能像仿真一样，测量某一个特定节点的变形量。

（2）温度对测量结果的影响，以基座材料铝合金为例，常温下铝合金的膨胀系数为2.3×10−5℃，内径为φ34 mm的基座孔，在温度浮动5 ℃的情况下，其变化约为0.004 mm。同样，带肩衬套尺寸也会因温度产生变形，虽然带肩衬套和基座的变化是同向的（同时变大或变小），但是由于基座和衬套的膨胀系数不同，两者的膨胀或收缩对带肩衬套内径收缩量产生影响。

3 结语

通过上述研究，在带肩衬套与基座的冷缩装配工艺中，采用有限元分析计算带肩衬套内径最大收缩量具有一定可行性，对修正带肩衬套内径公差带，使装配后带肩衬套孔径直接满足设计尺寸具有指导性意义。

（1）对φ64 mm带肩衬套进行有限元ABAQUS仿真研究，并通过冷缩装配试验进行验证，两者相对误差小于9%，获得了准确可靠的仿真环境，并且发现衬肩结构能够加强衬套的刚度，靠近衬肩位置，内径收缩量更小，冷缩装配后更不容易发生变形，在远离衬肩位置，内径收缩量达到最大。

（2）基于材料力学理论推导式（8）可用于指导带肩衬套类组件装配过程中，带肩衬套内径收缩量理论研究。

（3）获得φ34 mm带肩衬套不同过盈量下，带肩衬套内径最大收缩量线性回归方程δa=−2.31448×10−4+0.69441δ，最终仿真结果与试验结果相对误差小于13%，可应用于实际加工装配过程。