飞机电缆管状屏蔽层损伤转移阻抗计算分析

徐 骏

（江苏工程职业技术学院，南通 226007）

0 引言

随着多电飞机技术的发展，飞机机载系统整体性能得到提升，所处的电磁环境日趋复杂。相较于其他机载设备，飞机电缆因捆扎、安装、敷设的多样构型和受震动、冲击、雷电、串扰等影响的不稳定工作环境而更易出现故障，其中包含屏蔽层损伤故障。屏蔽层是机载电缆对抗电磁干扰的主要手段，所以屏蔽层的损伤必然导致电缆屏蔽性能降低，这将无法保证信号传输的精确性和完整性。飞机系统的信号传输与飞行安全息息相关，信号传输误差可能导致不安全事件发生，所以屏蔽层损伤是危及飞行安全的风险要素。目前针对电缆的屏蔽效能已有大量研究。国外，Schelkunoff[1]提出管状屏蔽层转移阻抗的计算公式。Vance[2]提出多种常见类型屏蔽电缆转移阻抗的理论计算和实际测量方法。后续很多学者包括Tyni、Kley 等针对Vance 提出的理论模型做了改进和完善。[3-4]这些研究主要集中在编织型屏蔽电缆的孔缝耦合和编织电感，使模型计算有效性得到提高。国内，有研究者通过波动方程理论和转移阻抗理论相结合来分析管状屏蔽体的屏蔽效能；[5]有学者基于Vance 模型详细推导了编织型屏蔽电缆的转移阻抗计算公式；[6]有学者基于有限元仿真分析球形孔洞损伤对电缆屏蔽效能的影响。[7]以上研究多为完好屏蔽电缆的屏蔽效能研究，涉及的屏蔽层损伤仅为球形损伤，而对更为常见的由于振动、碰撞、划伤等原因造成的长矩形损伤缺乏研究。本文通过解析计算的方法建立长矩形损伤前后管状屏蔽层损伤转移阻抗的解析模型，分析损伤尺寸和角度等参数对转移阻抗的影响并利用MATLAB 对典型算例计算后进行数值分析，为制订电缆屏蔽层损伤的相关标准提供理论依据。

1 理想管状屏蔽层转移阻抗计算与分析

1.1 转移阻抗理论

转移阻抗的概念由Schelkunoff 在1934 年提出，用来表征外部干扰电磁场对屏蔽电缆的电磁耦合能力。转移阻抗是电缆屏蔽层固有参数，转移阻抗越小屏蔽效能越好。[8]GB/T 17737.1—2013[9]给出了转移阻抗的明确定义，即单位长度屏蔽电缆芯线和屏蔽层之间的开路电压与屏蔽层上的感应电流的比值。转移阻抗的示意图如图1 所示，表达式为：

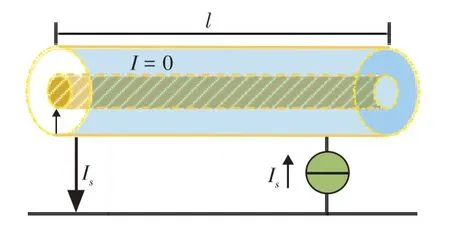
图1 转移阻抗的定义示意图

式（1）中Zt为转移阻抗，Is为屏蔽层上感应电V0为屏蔽电缆芯线和屏蔽层之间的开路电压，l 为电缆长度，I 是电缆芯线上的电流。

转移阻抗的理论计算一般通过上述定义式结合电磁场理论进行推导，且不断迭代出更加直观准确的解析式。一般来说，解析式的推导要根据屏蔽层的构型进行。机载屏蔽电缆屏蔽层根据构型不同可以分为管状屏蔽层、螺旋缠绕状屏蔽层和编织网状屏蔽层。3 种屏蔽层构型不同，呈现出的抗电磁干扰的特性也不同，其中管状屏蔽层电缆由于较好的高频特性而被广泛应用于机载电子系统。[10]本文研究管状屏蔽电缆屏蔽层损伤前后转移阻抗的解析计算方法并进行参数分析。

1.2 理想管状屏蔽层转移阻抗计算

理想管状屏蔽电缆结构如图2 所示，由外向内依次是电缆护套、管状屏蔽层、绝缘介质层、电缆芯线，屏蔽层截面积均匀、结构完好。受到外部电磁场干扰时在电缆屏蔽层外表面将产生感应电流，感应电流由于散射现象将逐步由屏蔽层外表面向内表面扩散。内表面的感应电流将在电缆芯线和屏蔽层内表面之间形成感应电磁场，从而将电磁场能量耦合至芯线。根据耦合机理，Schelkunoff[1]推导出管状屏蔽层转移阻抗表达式：

图2 理想管状屏蔽电缆结构图

式（2）中Zt为转移阻抗，R0为单位长度屏蔽层的直流电阻，T 是屏蔽材料厚度。设屏蔽材料电导率为σ，内外半径的平均值为a应作用引起导体截面上电流分布不均匀，越接近导体表面电流密度越大，这种现象称为“趋肤效应”[11]，效应大小用趋肤深度值来表示。设μ 为真空磁导率，f 为外部干扰电磁波频率

1.3 理想管状屏蔽层转移阻抗算例分析

本文以Pasternack Enterprises 公司生产的RG-401 型同轴电缆为例进行计算分析。电缆屏蔽层结构参数如表1 所示。首先，在MATLAB 中以外界干扰电磁波频率f 为变量，定义f 为1 个数组，取值在0 到107Hz 之间，每隔 1 000 Hz 采样 1 次，即 f = [0:1000:107]。其次，按照表1 所示，将公式（2）和R0、δ 的计算式中所涉参数赋值后进行数组运算，得到干扰电磁波频率在0～107Hz 内变化时屏蔽层转移阻抗Zt和干扰电磁波频率f 之间的关系，如图3 所示。由图3 可知，当频率低于10 kHz时，转移阻抗基本不变，约为 1.8×10-3Ω/m；当频率高于 10 kHz 时，转移阻抗随频率增大而减小，直至接近0。转移阻抗值越小，电缆屏蔽层屏蔽效能越好，可见，RG-401 电缆的高频抗干扰性能好。

图3 屏蔽层转移阻抗和干扰电磁波频率函数关系图

表1 RG-401 屏蔽层结构参数

2 长矩形损伤屏蔽层转移阻抗计算与分析

2.1 长矩形损伤屏蔽层转移阻抗计算

1)损伤模型的建立。在实际线缆损伤问题中，损伤的原因和损伤的状况是多种多样的。本文以具有代表性的长矩形损伤为例分析讨论损伤状况对线缆屏蔽层转移阻抗的影响。假设将管状屏蔽层展开成矩形后，矩形长边长度为L，短边长度为W，长边与线缆方向的夹角为α，则损伤屏蔽层模型图和展开示意图见图4、图5。

图5 管状屏蔽层损伤展开示意图

2) 计算公式的推导。在发生图4 所示损伤时，外界干扰电磁波可通过损伤直接耦合到电缆芯线上，所以屏蔽层的屏蔽机理发生了变化，相应的转移阻抗计算也必然需要考虑损伤处由于干扰电磁波的透射而引起的电感效应，耦合电感大小记作M。同时，由于屏蔽层损伤造成的屏蔽层直流电阻变化也需要被考虑，损伤后的屏蔽层单位长度直流电阻记作R′0，因此损伤后的屏蔽层转移阻抗Z′t可以写作：

图4 管状屏蔽层长矩形损伤模型图

式（3）中，角速度ω=2πf。由Bethe 的偶极子理论可知耦合电感M 表征的是屏蔽体孔径耦合时孔径的磁极化特性[12]，设磁极化系数为m，则M

R′0的计算涉及屏蔽层损伤导致的屏蔽导体有效截面积的变化，如图6 所示。首先利用微元法将屏蔽层圆柱管状导体等效为n 个相同圆柱导体微元的并联集合，在不考虑微元导体临近效应的影响下，n 越大，模型准确度越高。发生图6 所示损伤时，屏蔽层损伤处截面相应数量的微元导体失效导致屏蔽导体的有效截面积减小。设损伤处对应的弧长为H，则H 的大小应为长矩形损伤在截面处的投影。当屏蔽层厚度相对于半径忽略不计时，可以在图7 中定义H 的大小为损伤长矩形ABCD 在屏蔽层展开图上的最高点A到CE（过最低点C 且平行于线缆方向的线段）的垂直距离。因为长矩形在展开图的最高点和最低点会随夹角α 的大小发生变化，变化周期为π/2，所以定义夹角α 的取值范围为[0，π/2]。因此H 可表示为：

图6 屏蔽层损伤的示意图

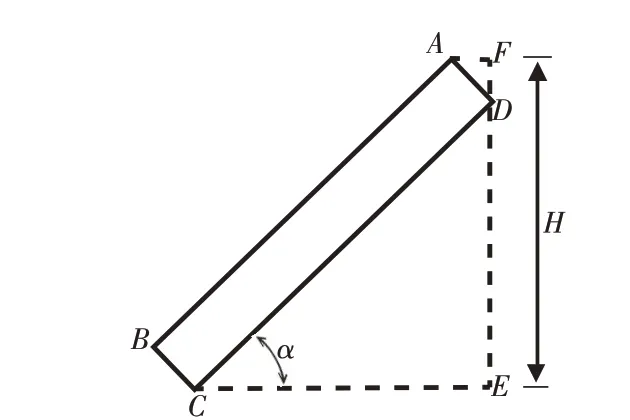
图7 管状屏蔽层损伤展开计算示意图

式（4）经三角函数变换可得：

其中：

由式（4）、式（5）、式（6）可知夹角α =π/2-φ 时，H 取最大值为 L2+ W2；α=0 时，H 取最小值为W。设屏蔽层完好时的截面积为S1，损伤后导体有效截面积为S2，则R′0可表示为：

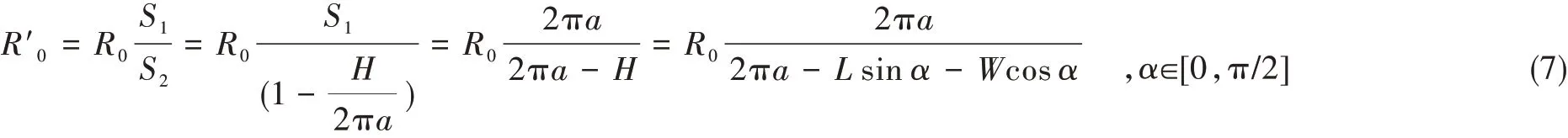
因此，当 H 取最大值，即 α =π/2-φ 时，R′0取最大值；H 取最小值，即 α=0 时，R′0取最小值。

2.2 长矩形损伤算例分析

以RG-401 型同轴电缆长矩形损伤为例进行计算分析，本文主要研究各损伤参数对屏蔽层转移阻抗的影响，所涉参数主要为损伤尺寸（L、W）、损伤长边与线缆方向的夹角α。因此，在MATLAB 中以外界干扰电磁波频率 f 为变量，定义 f 为 1 个数组，取值在 0 到 109Hz 之间，每隔 100 kHz 采样 1 次，即 f=[0:100000:109]。电缆损伤状况长边L 的值参考屏蔽层周长（D =2πa）设置，分别设置L = D/4 = 4.6 mm、L=D/2=9.2 mm、L = 3D/4 = 13.7 mm；为保证损伤的模型准确且便于分析，损伤短边W 的值参考L 的值设置（W = L/10）；损伤长边与线缆方向的夹角α 分别取90°、45°、0°。在MATLAB 中对式（3）、式（4）、式（5）、式（6）、式（7）所涉参数赋值后进行数组运算，得到屏蔽层转移阻抗随频率变化函数关系图如图8、图9、图10 所示。

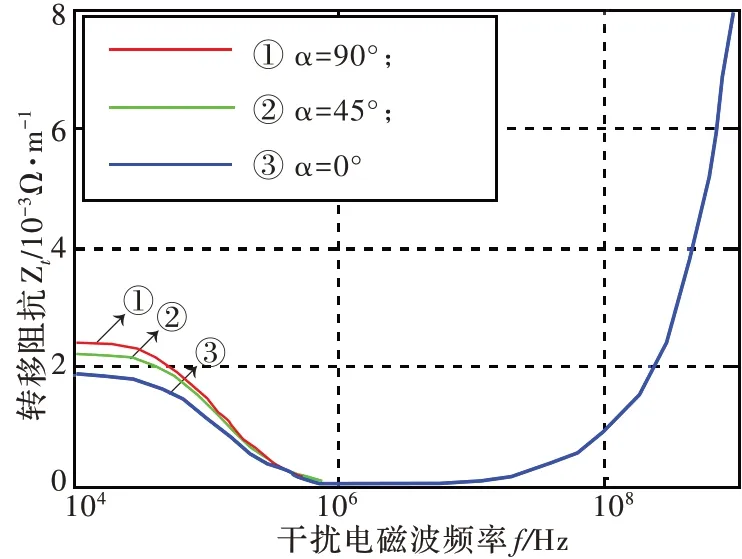
图8 L = D/4 = 4.6 mm 时转移阻抗随频率变化函数关系图

图9 L = D/2 = 9.2 mm 时转移阻抗随频率变化函数关系图

观察图8、图9、图10 可知，相同损伤尺寸下，损伤长边与线缆方向的夹角α 的大小影响低频时屏蔽层转移阻抗的大小，α∈[0，π/2-φ] 时，角度越大，转移阻抗越大。这是因为低频时转移阻抗主要取决于屏蔽层直流阻抗，损伤角度越大，屏蔽层有效截面积则越小，对应的直流阻抗也会越大，这点可以由式（7）看出。不同角度的转移阻抗都随频率值的增大而先减小后增大，但在高频时不同角度的3 条曲线汇成一条，表明高频时夹角α 的大小在相同损伤尺寸下对于转移阻抗的影响将没有差别。

不同损伤尺寸下，在夹角α 相同时，损伤尺寸越大，低频时曲线起始位置越高，即转移阻抗越大；高频时曲线越陡，曲率越大，即转移阻抗随频率变化的量越大。变化趋势也都是先减小后增大，这是因为低频时影响转移阻抗的主要是屏蔽层直流阻抗，高频时影响转移阻抗的主要是损伤处的耦合电感。由图8、图9、图10 可知，不同损伤尺寸下转移阻抗在频率为106Hz 时取最小值，表明发生上述损伤时，屏蔽电缆在频率为106Hz 时具有最优的屏蔽性能。

图10 L = 3D/4 =13.7 mm 时转移阻抗随频率变化关系图

不同损伤尺寸下转移阻抗的变化趋势几乎相同，频率对转移阻抗的影响都是以106Hz 为最低点界分成低频和高频2 个部分，因此可以在低频和高频段分别取1 个频率研究相同频率下损伤各参数对转移阻抗的影响。在MATLAB 中给干扰电磁波频率f 赋值，f1=104Hz，f2= 108Hz。以损伤尺寸L 为变量，定义L 为1 个数组，取值在 0 到 1.5 cm 之间，每隔 1 mm 采样 1 次，即 L=[0:10-3:1.5×10-2]。损伤长边与线缆方向的夹角α 分别取90°、45°、0°。在MATLAB 中对式（3）、式（4）、式（5）、式（6）、式（7）所涉参数赋值后进行数组运算，可得屏蔽层转移阻抗随损伤尺寸L 变化关系图如图11、图12 所示。

观察图11、图12 可知，低频时损伤长边与线缆方向的夹角α 的大小影响屏蔽层转移阻抗的大小，且α∈[0，π/2-φ]时，角度越大，转移阻抗越大，转移阻抗的变化趋势都是随尺寸L 的增大而增大。但当夹角为0°（即损伤长矩形和线缆方向一致）时，转移阻抗几乎不受影响。高频时，夹角α 的大小将不影响屏蔽层转移阻抗的大小，转移阻抗的大小只与损伤尺寸L 有关，且随L 的增加而增大。

图11 f=104 Hz（低频）时转移阻抗随损伤尺寸L 变化关系图

图12 f=108Hz（高频）时转移阻抗随损伤尺寸L 变化关系图

3 结论

管状屏蔽层电缆发生长矩形损伤后屏蔽层转移阻抗的大小受损伤尺寸、损伤角度和干扰电磁波频率影响。损伤尺寸L 相同的情况下，损伤角度影响低频段转移阻抗的大小，转移阻抗随着频率的增加先减小后增加；损伤角度对转移阻抗的影响在高频段没有差别。高频时，转移阻抗随损伤尺寸L 的增加而增大，但当干扰电磁波频率在低频范围内且损伤角度为0°时，转移阻抗基本不变。