基于遗传乌燕鸥算法的同步优化特征选择
贾鹤鸣 李 瑶 孙康健
随着科技不断进步,每个领域都会产生庞大而复杂的信息和数据,为了处理如此繁杂的数据,数据挖掘和机器学习相继出现[1].在数据处理领域中,数据分类是一项基本工作,但是由于数据的庞大和复杂,使得数据分类成为一项具有挑战的研究课题,常见的数据分类方法有决策树法、朴素贝叶斯法、k-邻近值(k-nearest neighbor,KNN)和支持向量机(Support vector machine,SVM)等.贾涛等[2]提出了数据流决策树分类方法,引入单分类和集成决策树模型有效地处理了概念漂移问题;崔良中等[3]选择了改进朴素贝叶斯算法来解决近来机器学习中的数据分类时间过长的问题;王景文等[4]选择KNN算法进行了数据预测和分类,实现了对中医胃痛病的自动诊断,对诊断病理起到了重要作用;丁世涛等[5]提出基于传统SVM 的分类方法,通过文本数据以标题为突破口实现快速分类,提高了分类速度和分类精度.上述论文着重研究了几种常见的数据分类方法的工程应用,由于各类数据量庞大且冗杂导致数据分类领域面临较大的挑战,因而许多学者将研究领域进一步推向如何更好更快地进行数据预处理,将特征选择和分类方法结合从而提高分类准确度.
为了更好解决特征选择与分类方法结合的问题,研究者们通过引入优化算法对SVM 的内核参数寻优.Chapelle 等[6]提出了利用梯度下降法来选择SVM 的参数,为接下来对其参数进行优化的研究奠定了基础;刘昌平等[7]使用混沌优化的方法对SVM 的参数进行优化,得出最优解并增强了分类精度;刘东平等[8]通过对遗传算法的改进,利用其交叉变异部分更好地对SVM 内核参数进行优化,达到了预期的实验效果;王振武等[9]将粒子群算法改进后应用到SVM 参数优化上,体现了融合优化与SVM 方法结合的优越性;石勇等[10]提出非平行支持向量顺序回归模型,能够更好地处理大规模数据.Yu 等[11]提出了双边跨域协同过滤的SVM 分类方法,通过集成内在用户和项目特征,更好地在目标领域中构建分类的模型.上述研究表明,将优化算法融合至SVM 中具有一定的效果,但上述方法大多只是单一优化其内核参数并未从整体考虑数据相关性的问题.
因此,近年来研究者也开始将特征选择与优化算法相结合,提高精度并减少时间成本.Zhang等[12]首次提出了多目标粒子群成本的特征选择方法,告别了传统的单目标特征选择,是一种极具竞争力的特征选择方法;2017 年,文献[13]提出基于返回代价的二进制萤火虫的方法,并将其应用到特征选择问题中,有效地提高了分类精确度并减少了所选特征个数;2018 年,张文杰等[14]将遗传算法应用到大数据特征选择算法中,提升了算法的搜索能力和获取特征的准确性;2019 年,李炜等[15]将改进的粒子群算法应用到特征选择当中,有效地降低了学习算法的数据维度和计算成本;同年,Jia 等[16]提出一种基于斑点鬣狗优化(Spotted hyena optimization,SHO)的特征选择算法,该算法提高了特征选择精度同时解决了特征冗余的问题;Baliarsingh 等[17]也在2019 年提出了基于帝企鹅优化算法(Emperor penguin optimization,EPO)应用在优化医疗数据的分类方法,大大减少了数据繁杂难以处理的问题;文献[18]提出了非负拉普拉斯嵌入引导子空间学习的无监督特征选择的方法,由非负拉普拉斯嵌入生成高质量的伪类标签,并利用伪类标签提供的判别信息,发展局部结构保持的子空间学习来寻找最优特征子集.受这些研究启发,本文将有效的优化算法应用到特征选择当中,筛选有效特征,更好地分类实际工程中的数据.
从工程应用的角度出发,为了进一步提高数据分类准确度,应该考虑将SVM 与特征选择相结合,利用优化算法对二者同时优化.齐子元等[19]提出同步优化特征选择和SVM 参数的方法,克服了单独优化二者的缺陷,但选用的优化方法过于陈旧,因此性能有待于提升;沈永良等[20]则提出了将改进烟花算法应用到特征选择和SVM 参数优化的方法,但大多对低维数据进行改善,对高维数据集的优势难以体现;Ibrahim 等[21]提出了基于蝗虫算法的同步优化方法,但未对本身优化算法做出改进,因此不能更加全面地应用到特征选择问题中.
由上述研究文献的分析可以看出,选择合适的优化算法对SVM 和特征选择进行同步优化是一个十分重要的研究问题,而元启发式优化算法主要分为进化算法和群智能优化算法两类[22].进化算法中以遗传算法(Genetic algorithm,GA)最为经典.通过模仿自然界优胜劣汰的理念,不断淘汰结果较差的解和有概率的交叉变异来更新最优解的位置[23];群智能优化算法则是模拟行为聚集的种群觅食行为,以粒子群优化算法(Particle swarm optimization,PSO)[24]为代表,它通过模仿鸟群飞行觅食的过程,不断更新飞行速度和位置以搜索到最优解.除此之外,还有一些仿生算法也属于元启发式算法,如鲸鱼优化算法[25],该算法模仿座头鲸捕食过程,利用独特的螺旋收敛方式模型不断靠近最优解.上述几种典型的优化算法都能在一定程度上解决工程中最优解的求取问题,但是由于工程问题的困难性和复杂性,优化算法很难独立解决所有实际问题.本文选择的乌燕鸥优化算法(Sooty tern optimization algorithm,STOA)也是如此,虽然它具有较强的全局搜索能力和一定的收敛精度,但根据没有免费的午餐定理[26]可知,没有任何一个优化算法可以独立解决所有实际问题,单一优化算法优化能力尚有不足,因此要想将优化算法更好地应用到实际问题上,就必须对其进行二次优化和改进.
由于乌燕鸥算法已经具备良好的全局搜索能力,所以对它的改进应当侧重于对其局部搜索能力的引导和改善.遗传算法的主要特点是能够对结构对象进行直接操作、具有较好的并行性和局部优化能力,同时它不需要特定的规则,能够根据概率自适应地调整搜索方向,因此近年来遗传算法在混合优化、机器学习、信号处理等领域得到了广泛的应用.2019 年,唐晓娜等[27]提出了混合粒子群优化遗传算法的混合方法,用来对高分遥感影像进行预处理,大大提高了其对城市用地信息的提取效果;2020 年,卓雪雪等[28]将蚁群算法和遗传算法结合并应用于求解旅行商问题中,将遗传最主要的交叉部分引入到蚁群优化中,解决了蚁群算法过早陷入局部最优解的问题,并加快了算法的收敛速度.由此可见遗传算法具有强大的局部搜索能力,将它与其他局部搜索能力不足的算法融合,便可以大大提高该类不足算法的收敛精度,同时也可以更好地避免陷入局部最优的情况出现.因此本文引入遗传算法,解决了传统乌燕鸥算法局部搜索不足且容易陷入局部最优的问题.
综合上述分析可知,本文主要创新研究工作如下:首先,本文根据平均适应度值概念提出遗传乌燕鸥算法,相较于传统乌燕鸥优化算法,具有更好的收敛能力和收敛速度;其次,基于本文遗传乌燕鸥算法,将其和SVM 及特征选择结合,用STOAGA 同步优化SVM 的C、ζ参数和二进制特征,并且对经典UCI 数据集进行测试,解决了数据预处理中分类精度不高、冗余特征过多的问题,可以有效完成数据分类工作;最后,将本文的特征选择模型应用到乳腺癌数据集中,通过10 次实验均入选的特征可以更好地辨别乳腺癌复发的主要因素,为解决乳腺癌数据的预处理提供了理论依据,使临床数据得到更妥善利用.通过验证,本文方法在数据预处理上确有较高的工程应用价值.
1 传统优化算法
1.1 乌燕鸥算法
乌燕鸥优化算法是2019 年针对工业工程问题,由Dhiman 等[29]提出的一种新的优化算法,其灵感来源于海鸟在自然界中觅食的行为.乌燕鸥是杂食性鸟类,以蚯蚓、昆虫、鱼等食物为生.这种算法具有很强的全局搜索能力,精度也较高.但仍存在一些问题如探索和利用之间的不平衡以及在迭代后期种群多样性低的情况,导致该算法容易收敛过早,同时这也促进了对优化算法进行改进的研究工作,使改进后的算法能够应用到更多优化问题上.
1.1.1 迁移行为(全局探索)
迁移行为,也就是探索部分,主要分为冲突避免、聚集和更新3 个部分.
1)冲突避免:
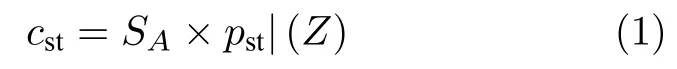
式中,pst表示乌燕鸥的当前位置,cst表示在不与其他乌燕鸥碰撞的情况下应当处于的位置,SA代表了避免碰撞的变量因素,用来计算避免碰撞后的位置,它的约束条件如式(2).
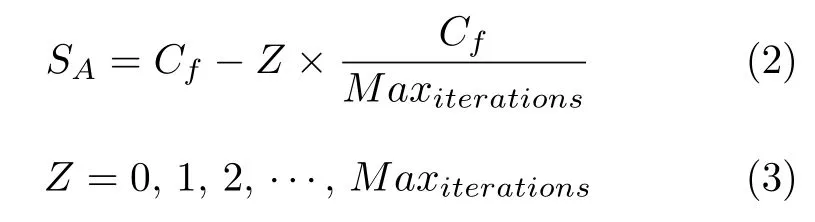
式中,Cf是用来调整SA的控制变量,Z表示当前迭代次数,因此SA从Cf到0 线性递减.本文中Cf值设置为2,因此,SA将从2 到0 逐渐减小.
2)聚集:聚集是指在避免冲突的前提下向相邻乌燕鸥中最好的位置靠拢,也就是向最优解的位置靠拢,其数学表达式如下:
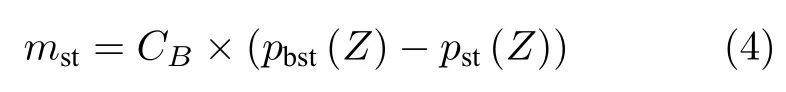
式中,mst表示在不同位置的pst向最优解的位置pbst移动的过程,CB则是一个使探索更加全面的随机变量,按照以下公式变化:
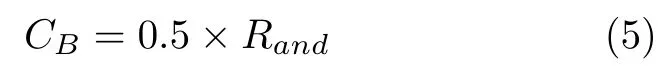
式中,Rand是0 到1 之间的随机数.
3)更新:更新是指在朝向最优解的位置更新轨迹,其轨迹dst的数学表达式为:

1.1.2 攻击行为(局部搜索)
在迁移过程中,乌燕鸥可以通过翅膀提高飞行高度,也可以调整自身的速度和攻击角度,在攻击猎物的时候,它们在空中的盘旋行为可定义为以下数学模型[30]:

式中,Radius表示每个螺旋的半径,i表示[0,2π]之间的变量.u和v是定义其螺旋形状的常数,在本文中均设定为1, e 是自然对数的基底.乌燕鸥的位置将按照下面的公式不断更新:

1.2 遗传算法
遗传算法主要通过选择、交叉和变异3 个步骤进行优化.选择过程是通过轮盘赌选择的方法来找到问题的最优解[31],将优化后的个体留给下一代.其中,每个个体被轮盘赌选中的概率为:Pi=i为个体,n为被选中的种群大小.交叉在遗传算法中起着核心作用,它指的是从两个亲本个体中置换和重组部件并产生一个新个体的操作,交叉概率表示为Pc=Mc/M,M表示群体中的个体数,Mc表示群体中交换的个体数.在遗传算法中,交叉是其全局搜索能力的主要过程,变异则是局部搜索能力的辅助过程.在遗传算法中引入变异过程的目的是利用遗传算法的局部随机搜索能力加速遗传算法向最优解的收敛,并通过保持种群多样性来防止遗传算法的过早收敛.变异概率表示为:Pm=B/(M ×l), 其中B为每一代变异基因的数量,M为每一代种群拥有的个体数量,l为每一代个体的基因链长度.在本文中,针对混合算法的局部性改善,将Pc和Pm的值固定化,使遗传算法以95%的概率交叉择优,同时有5%的概率变异以防止局部最优陷入[32].
1.3 遗传乌燕鸥算法
乌燕鸥算法是一种新型的元启发式算法,虽然已经应用于一些工业工程问题中,但仍存在一些不足,如探索和利用之间的不平衡、种群多样性低等问题.而遗传算法是一个运算简单但功能强大的算法,它作为一个部分嵌入到乌燕鸥算法中能够增强局部搜索能力.由于探索和利用之间的良好平衡对于任何元启发式算法都是至关重要的,因此本文将乌燕鸥算法与遗传相结合,加强了局部搜索能力,提高了搜索效率,并在后期迭代中保持了种群多样性.对于混合方式,本文采取先对平均适应度值进行评估的方式,平均适应度值代表了当前目标解的整体质量,对于最小化问题,如果个体的适应度函数值小于平均值,则表明粒子的邻近搜索区域是具有前景的,因此应采用增强局部搜索的策略.反之,如果个体的适应度函数值大于平均值,则不采用局部搜索策略[33].
遗传乌燕鸥算法在算法性能方面结合了乌燕鸥的全局优化性能,使得在大范围搜索的能力具有明显优势;同时,在局部收敛时又结合了遗传算法的优势,使得在寻优时规避局部最优陷入的可能,并加深局部搜索的能力.二者结合后,不论是探索和利用之间的平衡,还是寻优能力,都得到了改善,因此在算法的精度上得到提高,在收敛能力得到增强,在收敛速度上得到改善,并且在后期的迭代过程中还能继续维持其种群多样性.
针对遗传乌燕鸥的计算复杂度具体内容如下:

在STOA-GA 中,设置种群规模为N,其中在一次迭代中使用STOA 更新位置的个体数是n1,利用GA 更新位置的个体数是n2,即N=n1+n2,决策空间维度为d,该模型的时间复杂度主要分为位置更新和评价目标函数两部分,其中,Cof为评价目标函数的计算复杂度,Cos、Coc和Com分别为GA 算法中选择、交叉和变异的计算复杂度.由式(12)和式(13)可知,评价目标函数的计算复杂度是一致的,位置更新的复杂度具有明显差别.因此 只需对后者进行分析,从而评估计算复杂度的差异.在STOA-GA 中,根据平均适应度值将种群分为两部分,两部分的计算复杂度不同.选择、交叉和变异过程时GA 的主要代价,计算复杂度约等于O(n1×(d+Coc+Cos+Com)).对于使用STOA的部分,由于每个个体都需要在避免碰撞的前提下聚集,因此需要根据式(6)和式(11)进行位置更新,其计算复杂度则约为=O(n2×n×d).而在传统STOA 算法中,位置更新的复杂度约为=O(n2×d),即.由式(12)和式(13)可以看出,对于位置更新的计算复杂度都有3 项,显然,前两项的计算复杂度都小于STOA.对于第3 项,由于变异发生的概率仅有5%,因此可暂不考虑,从而仅剩下对选择和变异过程的计算复杂度未进行对比,可以看出在总体上计算复杂度相差不多,后续实验也证明了混合算法的计算复杂度具有一定竞争力.
STOA-GA 算法的伪代码和流程见图1 和表1,可以看出,STOA-GA 通过比较平均适应度值,使前期大范围搜索时采用STOA 的收敛方式,而在后期局部搜索时采用GA 的收敛方式,从而减小传统STOA容易陷入局部最优的可能并增强收敛能力.也就是说,遗传乌燕鸥算法是将GA 作为一个部分嵌入到乌燕鸥算法中,增强局部搜索能力,提高搜索效率并在后期迭代中保持种群多样性,具有更优秀的搜索能力和收敛精度.
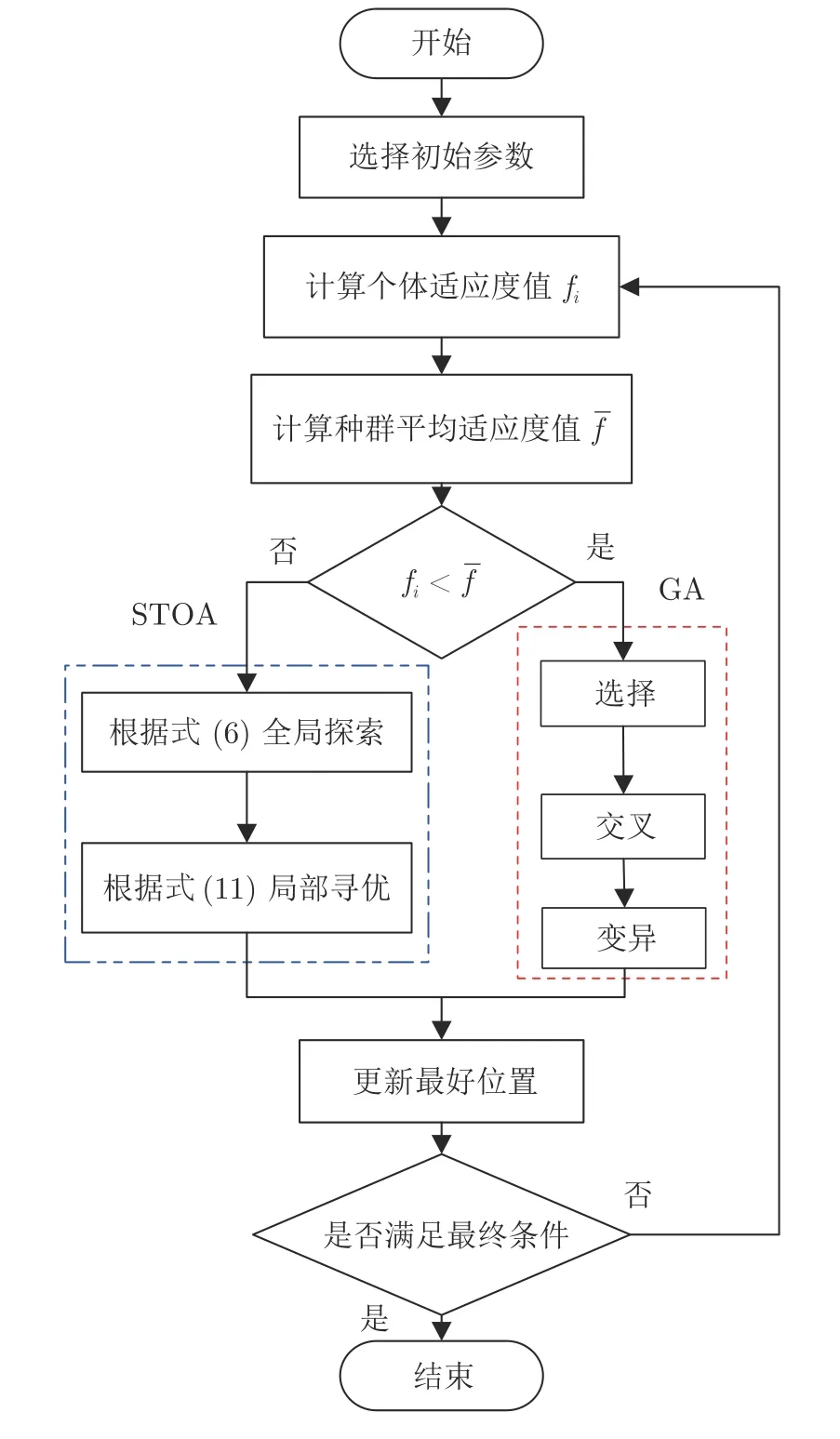
图1 STOA-GA 的流程图Fig.1 Framework of the STOA-GA
算法1.STOA-GA 算法的伪代码

2 混合优化算法模型
2.1 支持向量机
支持向量机是Cortes 等[34]开发的一种非线性二分类器,其原理是在高维向量空间中构造线性分离超平面,模型定义为特征空间中间隔最大的分类器,再转化为凸二次规划问题的求解.和其他机器学习方法相比,支持向量机具有较高的计算效率和很强的应用能力,因此广泛用于监督学习、分类和回归中.在线性可分的数据集中,支持向量机构造最优分离超平面将样本进行分类.设两类线性可分的数据集T={(x1,y1),···,(xn,yn)},xi ∈Rn,yi ∈{-1,1}.如图2 所示,空心圆和实心圆代表两类数据集.H为最优超平面,H1和H2为两类样本的边界,H1和H2之间的间隔称为分类间隔,落在H1和H2上的点称为支持向量.
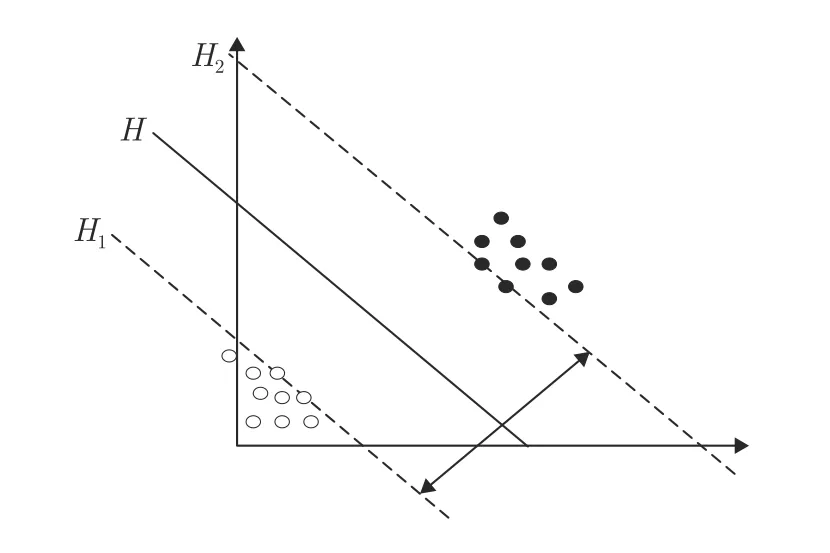
图2 SVM 最优超平面示意图Fig.2 SVM optimal hyperplane diagram
虽然线性分离超平面能够达到最优分类,但是在多数情况下属于不同类别的数据点不能够明确地分离,线性分类将会导致大量错误分类,因此,就需要将原始特征空间映射到更高维空间,找到一个可以正确分离数据点的超平面.
其核函数[21]主要有以下几种形式:
1)线性核函数形式:
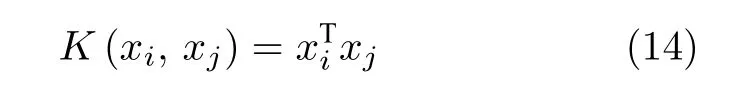
2)多项式核函数形式:
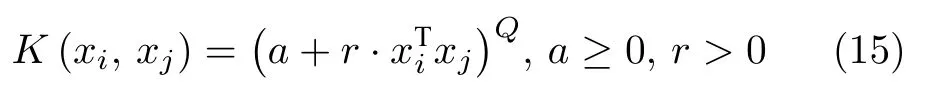
3)高斯核函数形式:
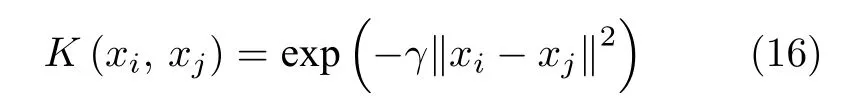
式中,K(xi,xj) 为核函数.由于线性核函数主要解决线性可分问题,而多项式核函数所要调节参数过多,因此本文后续实验选取可以映射到无穷维的高斯核函数.
2.2 特征选择二进制方案
特征选择是把数据从高维降到低维的一种方法,在某个特定准则下,通过从初始特征空间寻找最优特征子集来得到最优分类结果[35],其评价标准主要是以分类精度和所选特征个数所决定.特征空间一般包括相关特征、无关特征和冗余特征三种.相关特征是指对分类结果具有明显影响的重要特征,无关特征是指对分类结果不产生积极影响的特征,冗余特征则是与相关特征有所关联,但冗余的选取不会对分类结果有明显改善.因此,如何选取最优特征子集,避免无关特征和冗余特征就显得十分重要.
根据Dash 等[36]的特征框架,特征选择主要由生成特征子集、评估特征子集、停止准则和结果验证4 个部分构成,基于特征评价策略可分为开环法和闭环法[37].原始数据采用某种搜索策略搜索特征子集,接着利用评价函数评价所搜寻到的特征子集,当达到了停止准则后,便停止继续生成新的特征子集,输出此时最优特征子集,否则将会继续产生新的特征子集,直到达到停止标准.本文 选取随机搜索策略作为特征选择的搜索策略,选择算法迭代次数作为算法停止准则,即达到实验所设定的迭代次数便结束算法过程.
特征选择的实质就是对问题进行二元优化,因此在使用乌燕鸥优化算法处理特征选择问题时,应当设定好二进制方案,由于特征选择的解限于{0,1}之间,因此用0 或1 表示解的结果,0 表示并未选择此特征,1 表示选择此特征[38].但是,在原始数据集中,数据取值范围参差不齐,小到0~1,大到千万级以上,这种数据会严重影响SVM 的分类效果,因此需要对数据集进行预处理.为了将数据集数据归一化到[0,1]范围,利用如下公式进行处理:
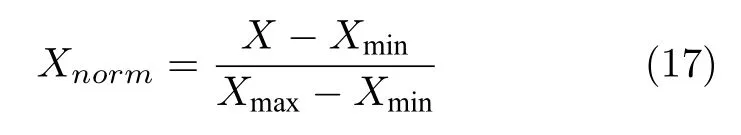
式中,X表示原始数据,Xnorm表示归一化后的数据,Xmin和Xmax分别代表此特征取值范围的最小值和最大值.
2.3 基于遗传乌燕鸥的优化特征选择模型
在构建SVM 的分类模型时,需要确定C和ζ两个参数.C为惩罚因子,代表分类过程对误差的宽容度,C越大,说明越不能容忍分类错误,因此常出现过拟合的状况,而C越小则会产生较大误差,出现欠拟合问题;ζ称为松弛变量,决定了数据映射到高维空间后的分布情况,ζ越大,样本相离超平面越远,支持向量越少,而ζ越小,样本相离超平面越近,支持向量越多.因此,SVM 分类结果的好坏与C和ζ的参数选择密不可分.
原有模式下的SVM,是根据所有特征先优化SVM 参数再进行特征选择,这就导致SVM 选择的关键特征在实际特征选择过程中并没有被选择,从而数据分类效果并不理想;反之,如果先进行特征选择再优化参数,那么每次训练过程都需要二次寻优,耗费时间成本过大,难以应用到实际问题中.因此,本文提出将SVM 的参数优化和特征选择同时进行的方法.搜索的维度变化为:惩罚因子C、松弛变量ζ和代表数据集特征的二进制字符串.
图3 为每个个体搜索维度示意图.前两个维度用来搜索惩罚因子C和松弛变量ζ,其余的维度用来搜索数据集中每个二进制特征,n为数据集中的特征个数.本文利用优化算法,同时对所有维度进行优化,对于SVM 的两个参数,粒子正常根据优化算法搜索其最优值,而对于数据集的n个特征,需要先对数据集的数据进行归一化处理,使数据都归一在[0,1],此时便开始对特征数据进行二进制处理,即:如果l1,l2,···,ln的解≥0.5 则该特征被选用,即取值为1;否则为0,特征不被选用.因此,l1,l2,···,ln的解便限于{0,1},接着利用遗传乌燕鸥方法搜索二进制特征,1 即为选用该特征,0 为未选用[21],最后将选出特征和SVM 的两个参数共同输入到SVM 里,使用交叉验证计算适应度值.

图3 每个个体的搜索维度示意图Fig.3 Schematic of search dimensions for each individual
本文模型在选择SVM 的两个参数同时,进行特征选择过程,保证了所选特征的准确性,避免落下关键特征,减少冗余特征,从而提高了分类准确度;相对于先进行特征选择再优化参数的方式而言,本文方法又在一定力度上减少了算法运行时间,因此,同步特征选择和优化参数更加可取.
算法2.基于遗传乌燕鸥算法的同步优化特征选择的详细过程如下[39]:
输入.数据集D,种群规模N,最大迭代次数Maxiterations,参数C的最大值Cmax和最小值Cmin,参数ζ的最大值ζmax和最小值ζmin,适应度函数的权重α和β,STOA-GA 所涉及的参数如Cf、CB、u,v、Pc和Pm.
输出.优化的特征子集,最佳参数C和ζ,对应的分类精度和适应度函数值.
1) 对数据集D内的数据归一化处理使数据都归一在[0,1]之间,然后将每一个特征进行二进制处理使特征的解限于{0,1}之间,并将数据集分为训练集D1和测试集D2;
2) 根据种群规模N和参数的最大最小值产生初始化种群;
3)将产生的支持向量的参数C,ζ和对应的特征子集输入到SVM 中完成训练和测试,由式(20)计算出粒子的适应度值fi;
4)根据适应度值fi求出;
5)如果fi <,根据GA 的选择、交叉和变异操作更新个体位置,否则根据STOA 的式(6)和式(11)更新当前个体位置;
6)将搜索后二进制特征的解为1 的特征从数据集挑选出来,并将数据集中选出的特征C和ζ、一起输入SVM,构造STOA-GA-SVM 分类器;
7)使用交叉验证计算适应度值,若有比当前最优解更好的解,则更新最优解;
8)判断是否达到最大迭代次数,若达到则输出最优值,否则跳转到3)继续运行.
基于遗传乌燕鸥算法的同步特征选择和SVM优化的流程如图4 所示.
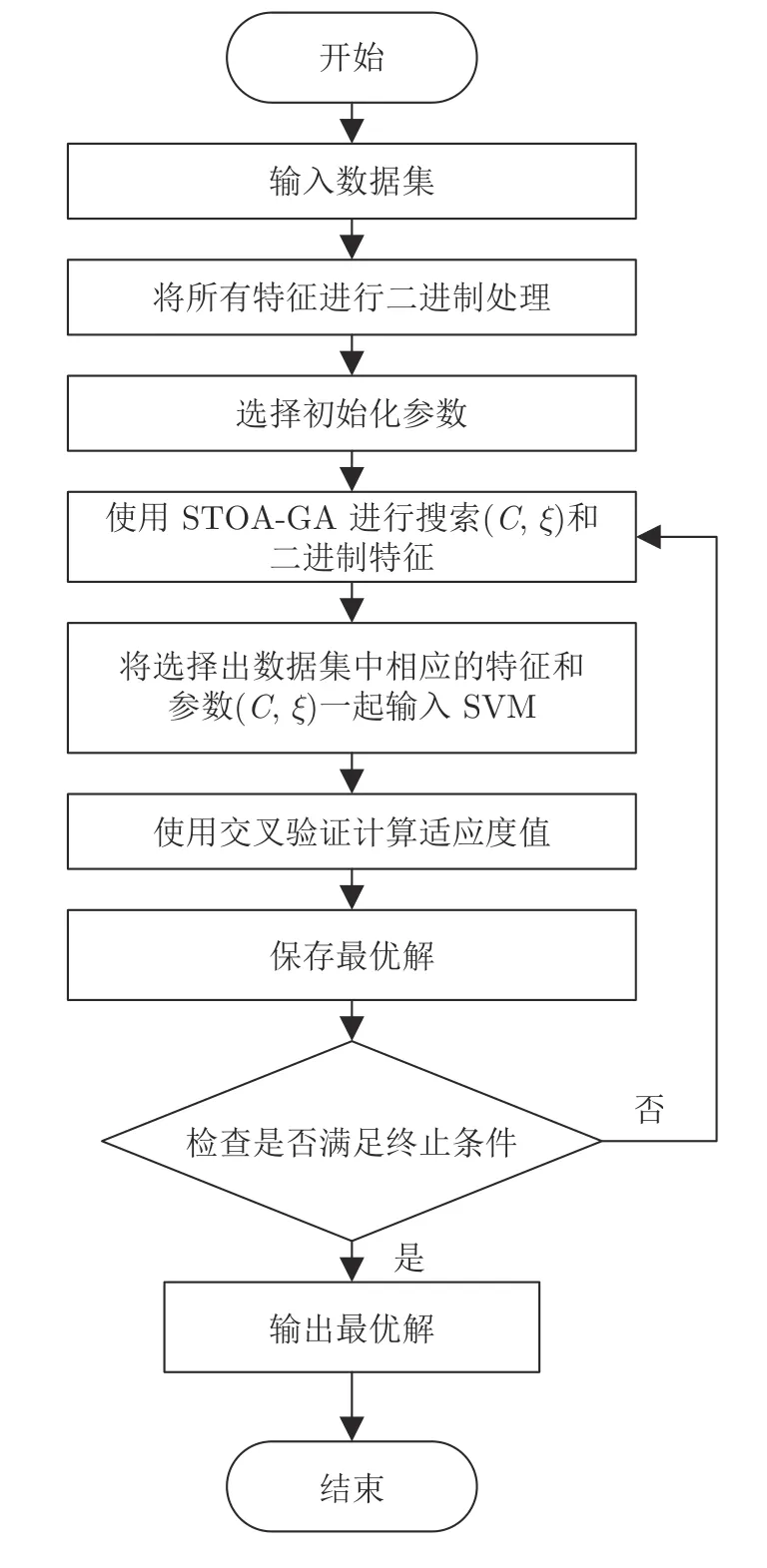
图4 混合算法的流程图Fig.4 Hybrid algorithm flow chart
3 实验设计及结果分析
3.1 实验设置
为了验证遗传乌燕鸥(STOA-GA)算法的有效性,本文采用UCI 数据库[40]中16 个经典数据集(其中包括6 个维数大于100 的高维数据集)进行仿真实验,从分类精度平均值、所选特征个数平均值、适应度平均值、标准差和运行时间平均值几个方面来对本文方法进行评估.同时,为保证实验客观全面,本文还选取了其他几种已经应用在特征选择领域的算法进行对比,分别是PSO、SHO、EPO 和未对其本身做出改进的GA 及STOA.结果表明,本文的混合算法能够准确应用在特征选择上,提高分类精度的同时避免选择无关冗余特征,对数据预处理有很大的帮助.
关于每个数据集的特征个数、样本数和类别数详细信息见表1.

表1 实验数据集Table 1 The data sets used in the experiments
在实验中,选择其他5 个算法作为对比算法,种群大小设置为30,最大迭代次数取100,为保证公平的原则,所有实验都在Intel(R) Core (TM) i5-5200U CPU @2.20 GHz 运行环境下,使用MATLAB R2014b 进行的,运行次数为30.对比算法的参数设置见表2.

表2 对比算法的参数Table 2 Parameters of the compared algorithms
3.2 经典UCI 数据集实验
为了更加全面客观地证明本文的优化算法在同时使用支持向量机和特征选择上的良好性能,本文采用以下6 个评价指标对本文方法进行测评:
1)分类精度平均值:表示实验中对于数据集的分类准确度的平均值,平均分类精度越高分类效果越好.其数学表达式如下:

式中,Accuracy(i)表示第i次实验中的分类准确度,M为运行次数.
2)所选特征数平均值:表示实验过程中所选择的特征个数的平均值,所选特征越少,说明去掉无关冗余信息效果越明显,公式如下:

式中,Size(i)代表算法在第i次实验中所选择的特征数.
3)适应度函数:特征选择主要的两个目标是分类精度和所选特征个数,理想结果就是选择特征个数较少同时分类精度较高.本文依据这两个标准来评价遗传乌燕鸥算法在支持向量机特征选择的应用效果.所选适应度函数公式如下:
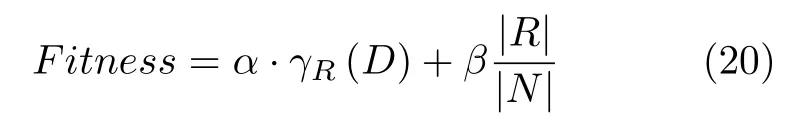
式中,参数α为分类精确性,代表分类精确度在适应度函数中所占比重,本文α取值为0.99[41].γR(D)代分类错误率,其表达式见式(21).其中,Accuracy表示分类的准确度;参数β为所选特征重要性,表示所选特征个数在适应度函数中所占权重,其中β=1-α,R表示所选特征子集的长度,即式(19) 的Size,N表示数据集的特征总数.
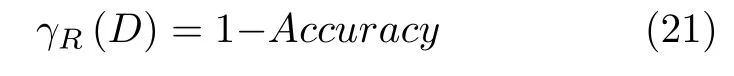
4)适应度平均值:表示实验中算法多次计算所得适应度解的平均值,适应度平均值越小说明特征选择在平衡加强分类精度和减少所选特征个数上的能力越强,可表示为:
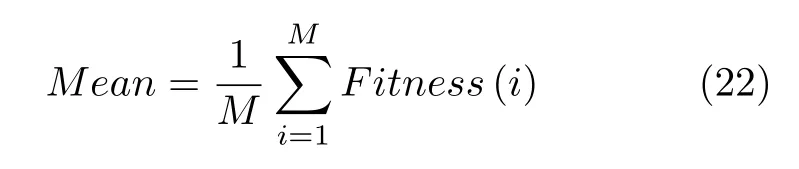
式中,Fitness(i)表示算法第i次实验中的适应度值.
5)适应度标准差(std):表示实验中优化算法的稳定性能力,标准差越小说明算法稳定性越好,表示如下:
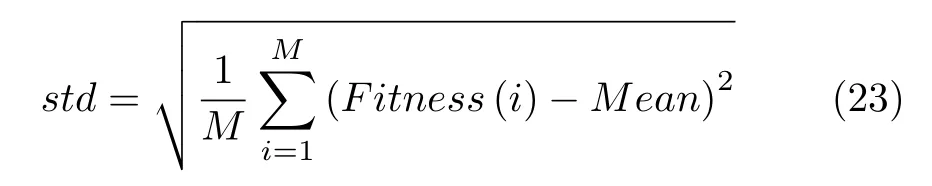
6)运行时间平均值:表示在实验过程耗费时间长短.众所周知,在工程实际中,时间成本也是重要因素.因此,在评价标准中加上此项来判定算法的优越性,计算公式如下:
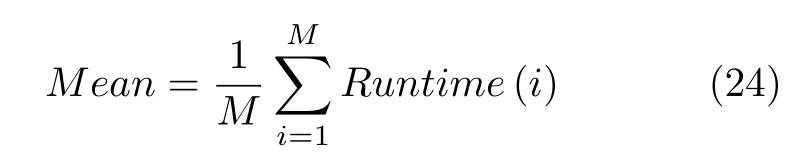
式中,Runtime(i)表示算法第i次实验中的时间.
由图5 可以看出,在分类精度上,除Hepatitis 和LSVT Voice 数据集外,本文算法能够准确对数据集进行划分,性能是最好的.由图5 还可看出,LSVT Voice 的整体分类精度不是十分优秀,此次实验属于偶然事件,不能一概而论.值得注意的是,本文算法在Tic-Tac-Toe 和Divorce predictors 两个测试集中都达到了100%的分类正确率,在Detect Malaciou 数据上也达到了99.73%的分类效果.由此可以证明,本文方法在同步特征选择和支持向量机上是具有竞争力的.
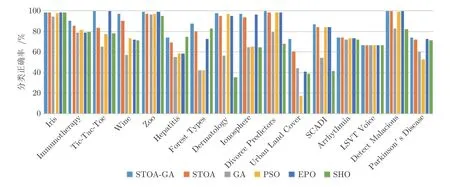
图5 各算法分类精度平均值Fig.5 The average accuracy of each algorithm
图6 是实验过程中所选择的特征个数平均值,可以看出,在多数情况下,本文的遗传乌燕鸥算法所选的特征个数都相对较少.虽然在Wine、Forest types 和Dermatology 数据集上本文算法并未得到最理想的结果,但是在大于100 维的数据集测试中,本文算法都是最优秀的.因此,相对于其他对比算法,本文的遗传乌燕鸥模型在数据降维问题的处理上具有优越性.
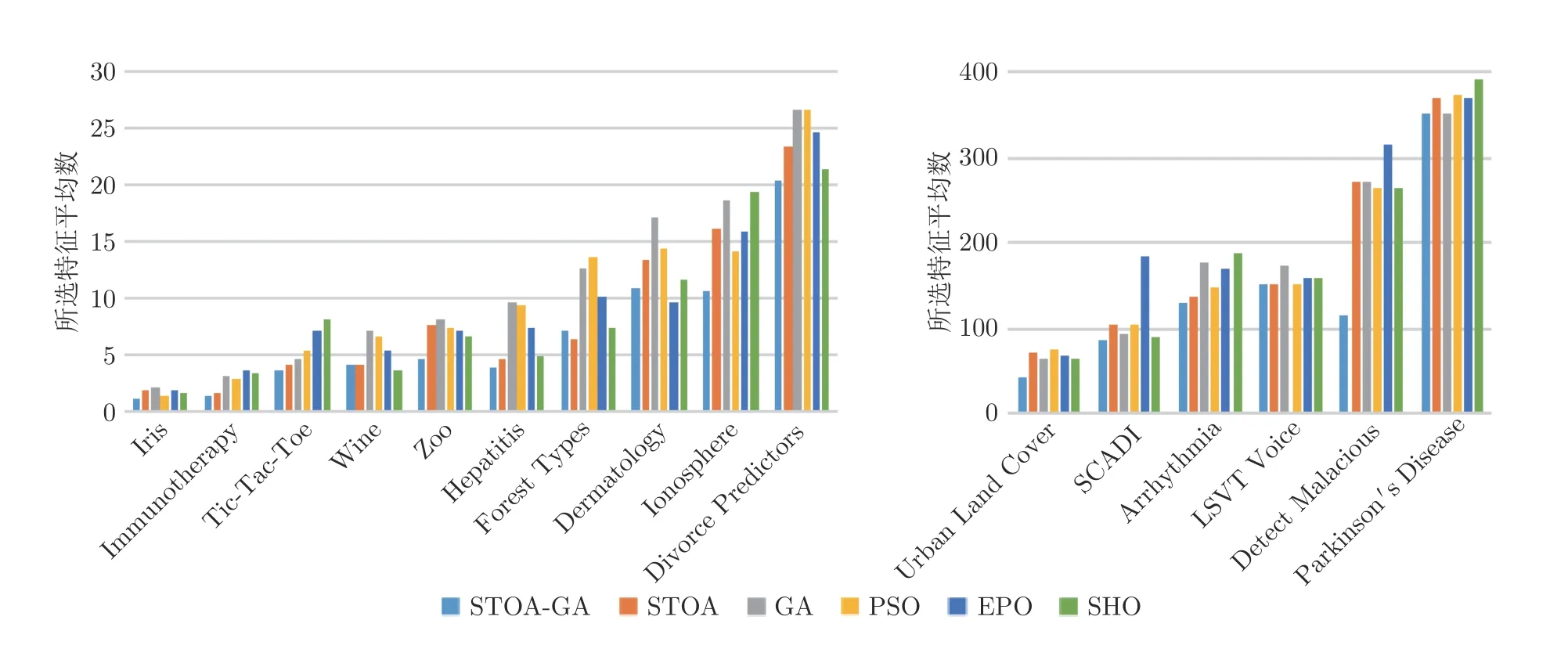
图6 各算法所选特征平均值Fig.6 The average value of the selected features of each algorithm
运行时间平均值见表3,可以看出,本文算法的时间优势并不十分明显,这是由于本文方法是将乌燕鸥和遗传混合,因此导致其时间上会较乌燕鸥原算法稍有不足.但通过仔细研究,可以看出虽然本文算法运行时间不是最短的却仍具有一定吸引力.因为乌燕鸥算法本身收敛较快容易早熟,因此将遗传算法和其融合后相较于普通遗传算法运行时间得到极大改善.同时可以看出,由于乌燕鸥本身时间上的优越性也导致在多数情况下本文的遗传乌燕鸥算法和其他对比算法相比仍具有时间优越性,所以遗传乌燕鸥算法在这方面的应用仍旧具有潜力.

表3 各算法运行时间平均值(s)Table 3 The average time of each algorithm (s)
结合前面所提到的分类精度平均值和特征选择个数平均值,可以验证本文的遗传乌燕鸥算法在同步特征选择和支持向量机的使用上具有十分广阔的前景,为更加清晰准确地证明这一点,表4和表5 对适应度函数结果进行了评价,可以看出,本文算法在不同维度的情况下,都能在平均值和标准差上表现出良好的性能,因此可以证明遗传乌燕鸥同步优化支持向量机的特征选择具有更高的精确度和相对优异的稳定性.图7 是算法在30 次运行中的最后一次实验的适应度值绘制成的收敛曲线,完整地表现了每个数据集的搜索收敛过程.由图7 可以看出,相对于其他对比算法,不论数据特征的维度如何,遗传乌燕鸥算法依旧能表现出较快的收敛速度、较高的收敛精度和较强的收敛能力.因此,通过实验更加清晰准确地验证了本文算法具有可行性.
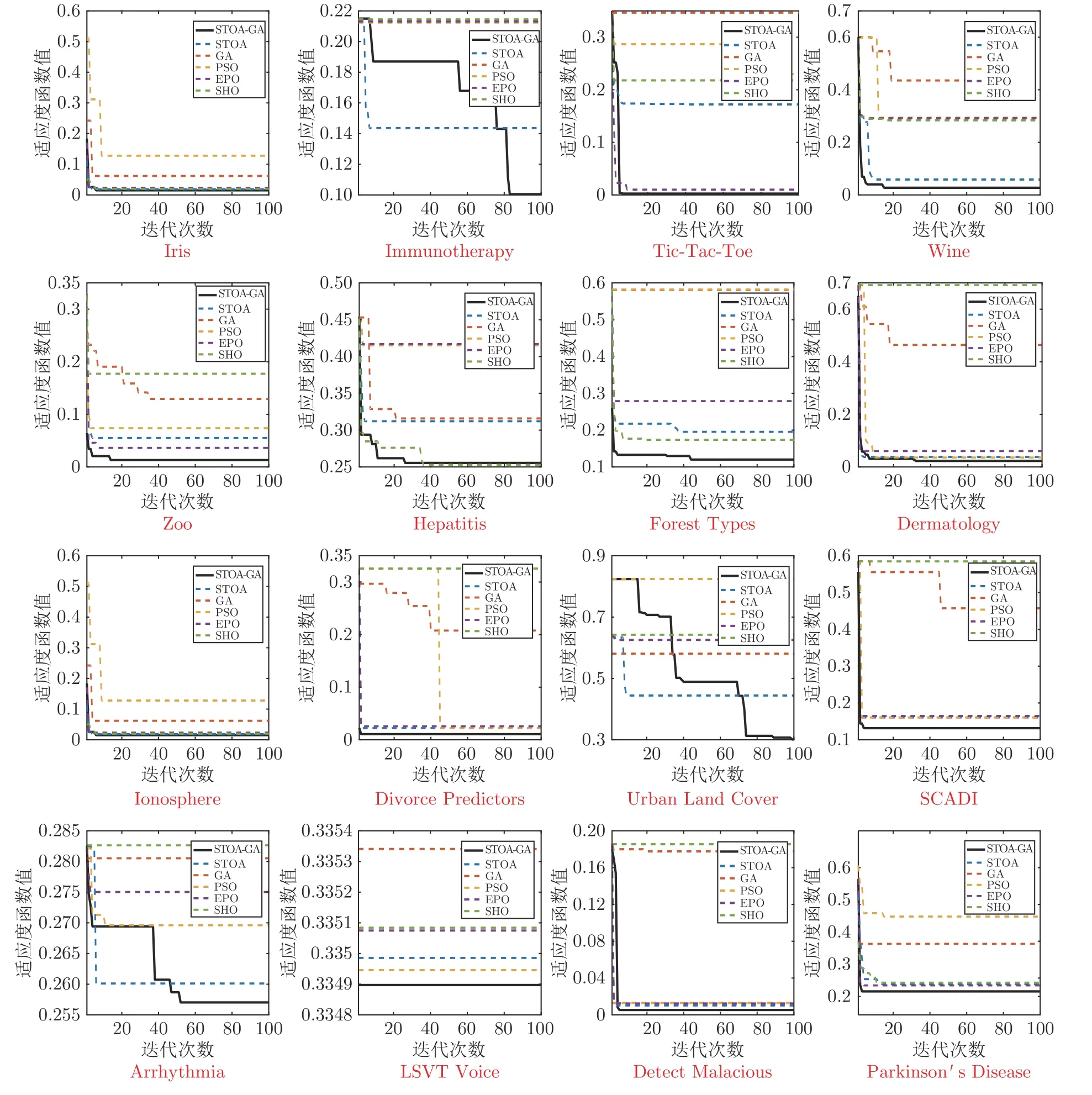
图7 各算法适应度函数收敛曲线图Fig.7 The convergence curve of fitness of each algorithm

表4 各算法适应度函数平均值Table 4 The average fitness of each algorithm
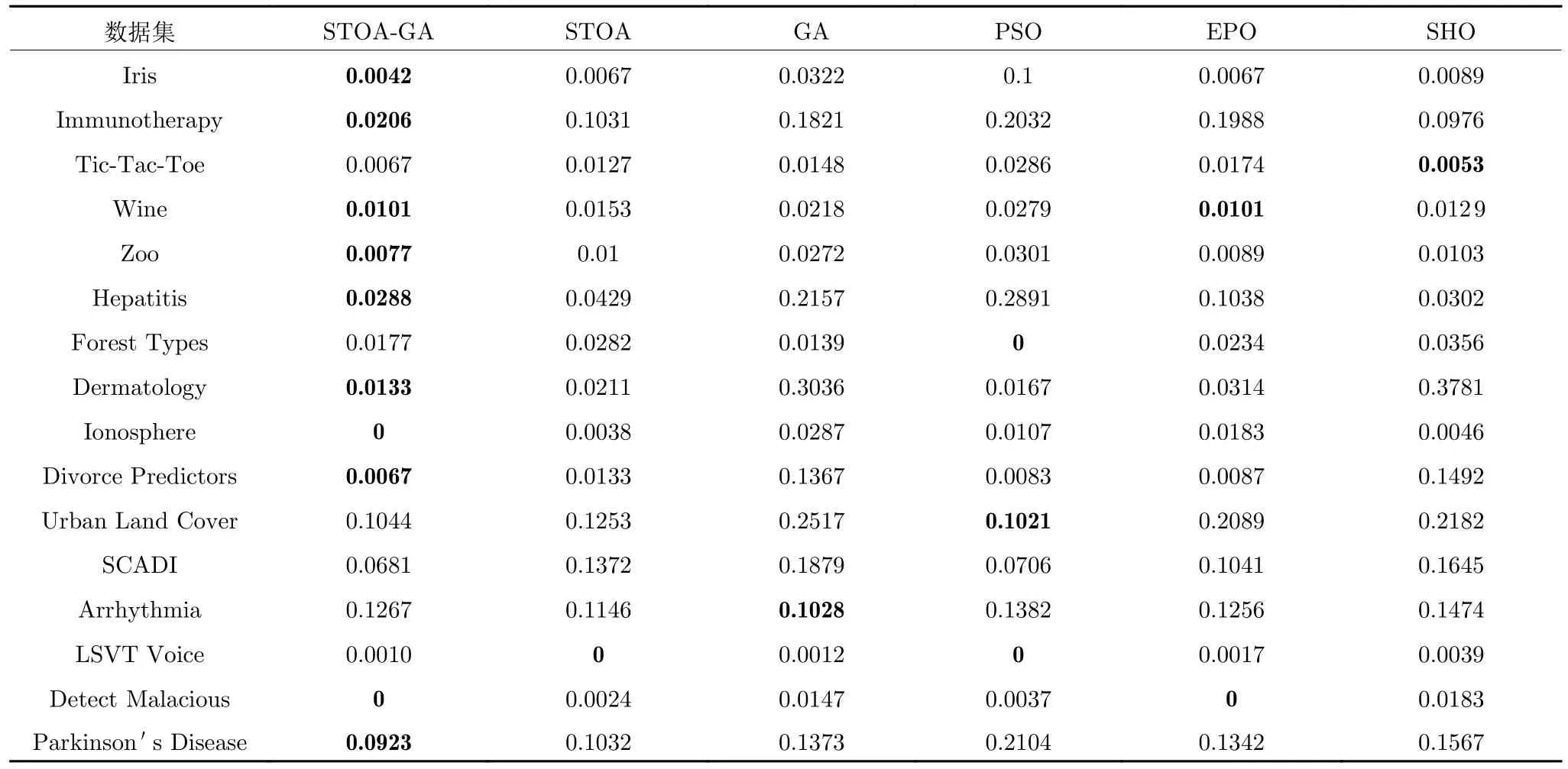
表5 各算法适应度函数标准差Table 5 The standard deviation of fitness of each algorithm
3.3 本文算法与其他算法实验
为了更加全面而客观地评判本文模型在数据预处理领域具有较好的前景,故将本文算法与其他常见的分类方法进行对比,分别应用决策树法(Decision trees,DT)、朴素贝叶斯法(Native Bayes,NB)、KNN、SVM 和本文遗传乌燕鸥算法(STOAGA)对5 组数据集进行实验分析.同时,为更加详细地对比普通分类方法,引入在普通二分类常用指标特异性和敏感性.特异性(Specificity)指模型对负样本的预测能力,特异性越高说明模型对负样本的识别率越好.敏感性(Sensitivity))指模型对正样本的识别能力,敏感性越高,模型对正样本的分辨率越准确,二者表示如下.
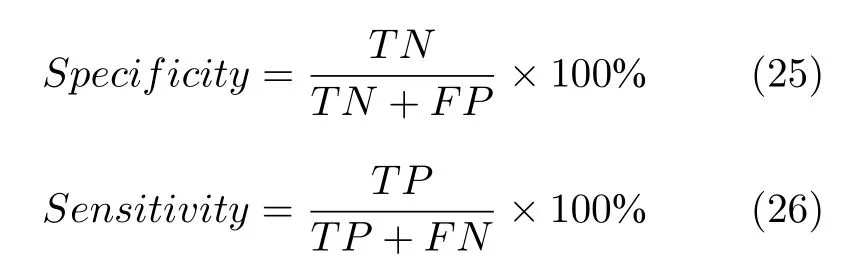
式中,TN(True negative)是指将负样本分类为负样本的个数.FP(False positive)是指将负样本分类为正样本的个数.TP(True positive)是指将正样本分类为正样本的个数.FN(False negative)是指将正样本分类为负样本的个数.
由于敏感性和特异性是二分类问题时的分类标准,故选取上述数据集中部分二分类数据集进行实验,实验结果见表6~8.可以看出,对于原始SVM分类方法,本文的应用优化和特征选择并行的模型对各项指标都有明显提升,而DT 和NB 方法虽然实验效果不足,但是由于其经典性,目前仍有研究学者使用.KNN 是另一种目前较为热门的分类方式,但是从实验结果可以看出,本文的模型在多数情况下都更具潜力,分类效果更为优异.
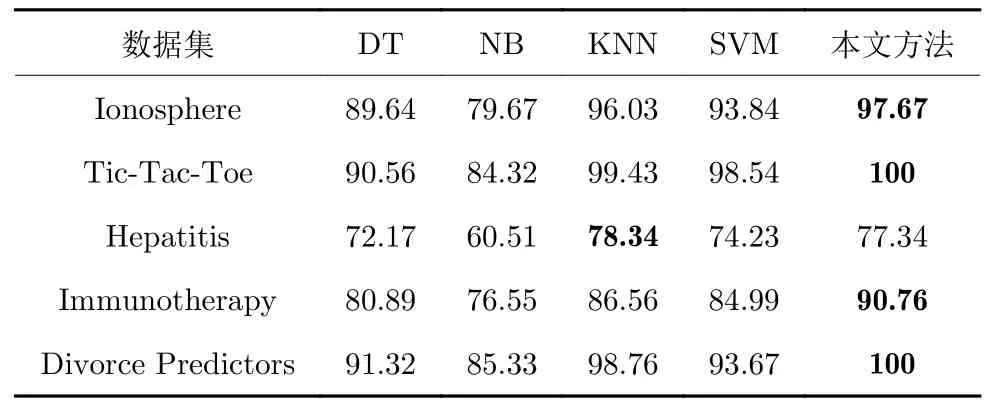
表6 各算法特异性(%)Table 6 The specificity of each algorithm (%)
经过这3 个指标的论证,本文模型在数据处理中应用较为稳定,能够较为准确地分类相关数据.通过对比经典的数据分类方法的实验结果,可以看出,本文方法在多数情况下都是最优状态,可以有效提高分类准确性和适应性.因此,本文方法是行之有效的,能够更好地改善分类特异性、敏感性和准确度.结合第3.3 节优化算法方面的比较,能够全面细致地证明本文的模型在数据预处理领域上具有广阔的应用前景,可以处理冗余复杂的数据集,为后续数据处理工作提供强大助力.
4 STOA-GA 算法在乳腺癌数据集中的应用
医学诊断领域是数据分类的重要领域,在面对冗杂繁多的临床数据时,医生很难从中获取有效信息.因此,越来越多的医疗工作者开始选取数据挖掘算法进行数据预处理,利用临床数据预测病情.乳腺癌是一种常见女性疾病,自20 世纪70 年代末以来,全球乳腺癌患病率一直呈上升趋势,而中国的发病率增长速度更是高出高发国家1~2 个百分点.因此,若能根据临床数据对各项指标作出预测,就能更好地预防该病的发生,从而有效减少患病率.
本文采用卢布尔雅那肿瘤研究所公开的乳腺癌数据集进行仿真实验[40].该数据集包含286 例人员的记录(其中201 名乳腺癌未复发患者和85 名复发患者),每位人员包含9 个特征,表9给出各特征的详细信息.
表10 为本文算法在乳腺癌数据集运行10 次的结果,其中平均分类准确率为97.51%,表明在绝大多数样本中,本文模型可以正确分类测试数据,平均选择特征个数为4.5,减少了50%的特征,有效地降低了数据的维度.其中,第5 次实验的分类准确率最高,为98.21%,所选特征数为4,适应度值为0.0222,运行时长为62.09 秒.特异性和敏感性可以评估模型的预测能力,其值越高,漏诊概率就越低,综上所述,遗传乌燕鸥算法对此数据集的处理效果十分优秀,更有利于医生诊断.
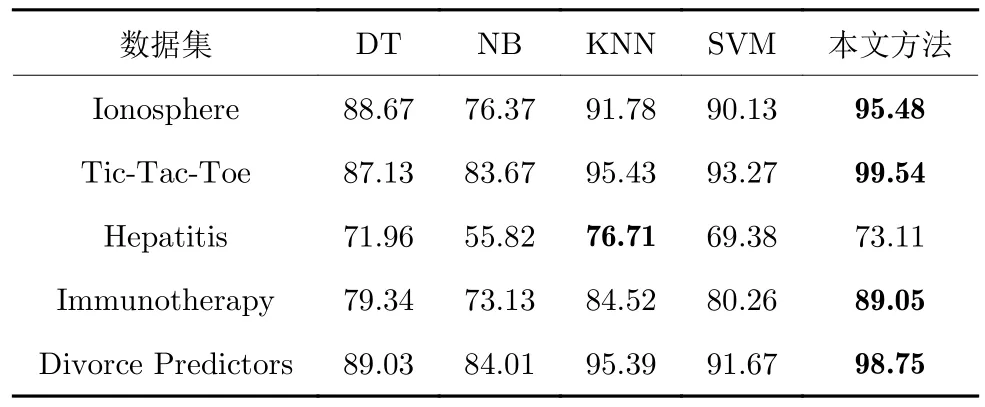
表7 各算法敏感性(%)Table 7 The sensitivity of each algorithm (%)

表8 各算法精确度(%)Table 8 The accuracy of each algorithm (%)
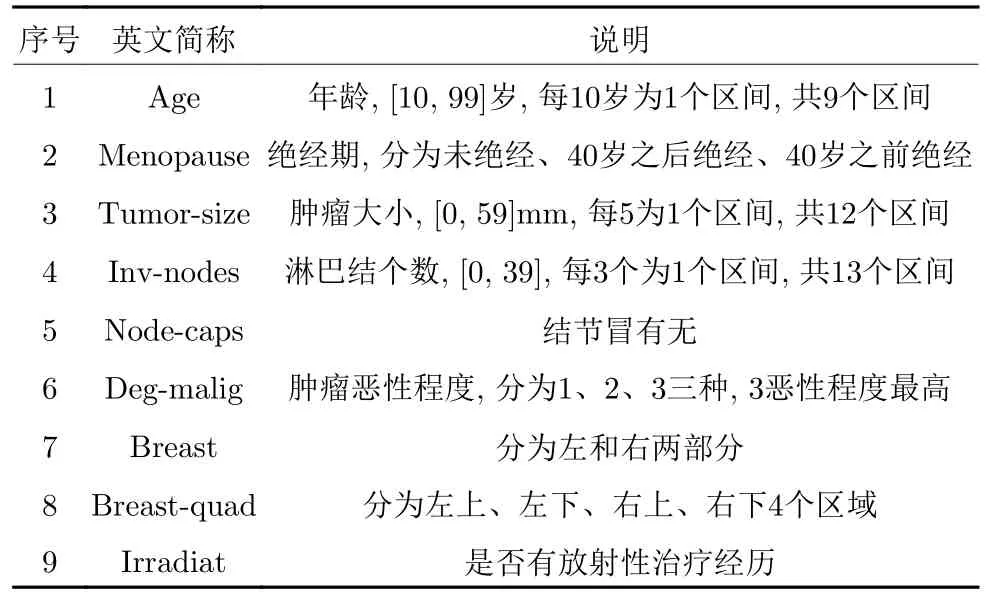
表9 乳腺癌数据集特征信息Table 9 The breast cancer data set feature information

表10 STOA-GA 算法的10 次实验运行结果Table 10 The results of 10 experiments of STOA-GA
表11 为10 次实验均选择的特征,代表着这些特征是区分是否复发患病的关键特征.这些特征有助于帮助医生判断是否存在乳腺癌复发的可能.当患者的临床特征与表11 中的特征大致相符时,就会有复发风险,需要进行进一步的诊断.根据选择特征可以看出,患病特征含有肿瘤过大且恶性程度高、淋巴结个数过多和有结节冒,那么就极有可能出现复发情况.

表11 10 次实验均入选的特征Table 11 The selected feature of 10 experiments
5 结束语
本文针对传统乌燕鸥算法中探索和利用之间的不平衡、种群多样性低等问题,提出遗传乌燕鸥算法,改善了算法的局部搜索能力和收敛能力,从而提高收敛精度,以便获得更加优秀的解.同时,将遗传乌燕鸥算法与支持向量机和特征选择结合,对特征和支持向量机的两个参数同时优化,提高对数据的分析学习能力.通过对经典UCI 数据集进行分类,并与STOA、GA、PSO、SHO 和EPO 等方法对比,实验结果可以看出,本文方法的最优搜索能力更加具有优势,可以有效完成数据分类工作.对于乳腺癌临床数据的成功应用,也证明了本文方法在筛选特征和分类精度上确有实效,为数据预处理提供了理论依据,使数据得到更妥善的利用.对于未来的研究,可以更加深入研究优化算法的混合模型,使其能够更好的应用于数据预处理领域.

