迭代学习模型预测控制研究现状与挑战

马乐乐 刘向杰 高福荣

在现代智能制造业中,批次生产方式占据越来越重要的地位,多用于生产具有高附加值的精细化产品[1],广泛分布在化工、冶金等传统重工业领域[2-4]和生物制药、人工智能、半导体制造等高新工业领域[5-7].批次生产过程通常具有特定的加工顺序,并通过重复操作批量获得同种产品,其控制目标通常为在有限时间区间内重复跟踪设定运行轨迹.

批次过程的本质特性明显区别于连续过程,可以归纳为 “多样产品”、“重复运行”、“时段切换”和 “变换指标”四个方面[8].自20 世纪90 年代起,由于产品种类增多、市场需求变化加快导致批次生产方式愈受青睐,批次过程控制也逐渐成为一项独立的研究课题.总体来说,批次过程控制研究历经了连续过程控制方法、迭代学习控制(Iterative learning control,ILC)和迭代学习模型预测控制(Iterative learning model predictive control,ILMPC)三个阶段,图1 显示了其发展历程.

图1 批次过程控制发展历程Fig.1 Development of batch process control

20 世纪90 年代,依托于连续过程控制理论的飞速发展,衍生了第一代批次过程控制技术.其核心思想是将批次过程视为有限时间内的连续过程,采用成熟的连续过程控制技术对批次过程进行时域控制,控制手段从传统的比例-积分(Proportion integration,PI)控制策略[9]逐步发展至模型预测控制(Model predictive control,MPC)[10-12]、模糊控制[13]、神经网络控制[14]等先进控制方法.但是连续过程控制方法没有考虑批次过程 “多重时变”的特有性质,难以解决实际批次过程的高精度轨迹跟踪问题.批次过程的动态变化具有双向性:沿时间方向,批次过程的设定值是时变的,需要在每个采样点跟踪不同的目标值;沿批次方向,各批次执行重复的生产任务,需要利用积累的控制经验不断提高跟踪性能.这种特殊的控制目标和控制结构激发了众多学者去探索基于迭代学习的批次过程控制方法.

迭代学习控制提出于20 世纪80 年代[15],最早应用于机器人控制.它对同一轨迹进行重复跟踪,以前一迭代次序中输出信号与给定目标的偏差修正下一迭代次序的控制信号,从而逐步提高系统的跟踪性能,最终实现有限区间上的完全跟踪.ILC 的迭代控制结构与批次过程重复操作的特点高度契合,能够实现批次过程高精度轨迹跟踪的控制目标.因此,从20 世纪90 年代中期开始,ILC 在批次过程控制中获得了广泛关注.韩国学者Lee 等最早将ILC 应用于聚合反应器控制[16],采用基于反馈的ILC 沿批次更新学习律,提高系统跟踪精度;随后,Lee 等结合最优学习律,提出基于二次型指标的Q-ILC(Quadratic-criterion-based ILC,Q-ILC)策略,显著提高了ILC 在批次过程中的学习性能.Lee 等在发表于Control Engineering Practice的论文中系统综述了ILC 应用于批次过程的几种形式,并集中讨论了实际应用中需要解决的问题[17].基于Lee 等的研究工作,后人针对批次过程的时滞、参数不确定性、随机干扰等问题,构造了鲁棒ILC 策略[18-21];针对批次过程的初态偏移及变参考轨迹等问题,提出了改进的自适应ILC 策略[22-25];此外,ILC 还与模糊规则、神经网络和数据驱动等技术结合,利用批次过程数据同时实施建模和控制[25-31].基于ILC的控制方法融合了批次过程有限时间重复操作的特点,沿迭代轴建立了批次间的控制关系,其产生和发展标志着批次过程控制正式独立于连续过程控制,形成了适应批次过程特性的迭代控制结构.

ILC 的应用将批次过程控制从时域引入迭代域,但是无论是传统连续过程控制方法还是基于ILC 的批次过程控制方法,其控制信号只作用于一个维度.在时域上,ILC 是典型的开环控制,不具备抗实时干扰能力,无法保证系统的闭环稳定性和鲁棒性.根据ILC 的控制结构,当前批次出现的干扰和偏差直到下一批次才能被处理,导致批次过程的时域跟踪性能下降.因此,将ILC 算法与成熟的时域控制技术结合成为了批次过程控制研究的新方向.文献[32-33]尝试将ILC 算法与传统比例-积分-微分(Proportion integration differentiation,PID)控制策略结合,利用ILC 沿批次进行设定点迭代学习.但是PID 控制只适用于调节问题,而批次过程的设定值是时变的,PID 控制无法满足批次过程高精度轨迹跟踪的控制要求.MPC 能够根据系统模型预测未来的状态及输出,在当前时刻的滚动时域优化中直接采用时变的设定值轨迹作为目标输出,因而在轨迹跟踪控制方面具有突出优势[34-35].将ILC 与MPC 结合不仅能保留ILC 的批次学习能力,同时可以大大提高时域闭环跟踪性能,由此形成的迭代学习模型预测控制(ILMPC)标志着批次过程控制进入二维(Two-dimensional,2D)控制时代,其算法结构如图2 所示.ILC 根据历史数据以批次为单位更新全区间控制律,MPC 在各批次内通过预测未来系统状态和输出进行滚动时域优化获得当前时刻的控制信号.

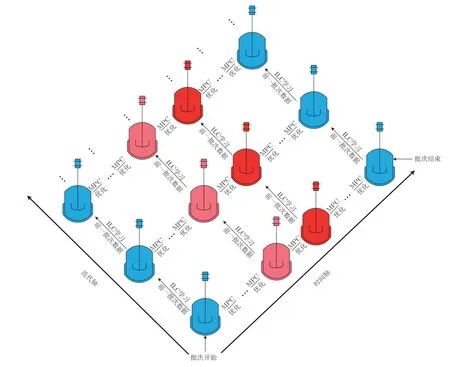
图2 迭代学习模型预测控制结构Fig.2 Structure of ILMPC

加拿大学者Bone 于1995 年在Automatica期刊上首次提出将ILC 与广义预测控制(Generalized predictive control,GPC)结合[36],利用ILC 的学习能力改善GPC 在重复性干扰下的控制效果,形成了ILMPC 算法的雏形;韩国学者Lee 等于1999 年在AIChE Journal发表的论文中结合ILC和模型算法控制(Model algorithm control,MAC)建立了批次模型预测控制(Batch model predictive control,BMPC)策略,并首次将ILMPC 算法应用于间歇反应器控制[37];2000 年,Lee 等在IEEE Transactions on Automatic Control期刊上对BMPC 的收敛性进行了严格的理论证明[38],将ILMPC 的理论研究推向新的高度;文献[39-40]在BMPC的基础上,令ILC 和MPC 分别作用于批次方向和时间方向,形成经典的两段式ILMPC (Twostage ILMPC) 控制架构.

历经20 多年的发展,ILMPC 已经成为批次过程控制领域的主流方法[41].本文将在分析现有成熟的迭代学习模型预测控制理论的基础上,指出其面临的挑战,综述该领域的研究动态,并展望迭代学习模型预测控制的未来研究方向.本文的结构框架及主要内容如图3 所示.

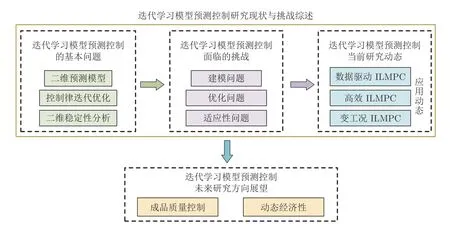
图3 结构及主要内容Fig.3 The structure and main contents

1 迭代学习模型预测控制的基本问题

在由ILC 和MPC 共同作用的2D 控制框架下,ILMPC 算法的模型搭建、控制律优化及跟踪性能分析都需要从时间轴和迭代轴两个方向同时进行.综合来看,ILMPC 的理论体系包含三个基本问题:二维预测模型建立、控制律迭代优化以及二维稳定性分析.

1.1 二维预测模型

MPC 的预测功能需要基于预测模型实现,预测模型的形式灵活多变.在经典的MPC 理论中,MAC 采用的脉冲响应预测模型和动态矩阵控制(Dynamic matrix control,DMC)采用的阶跃响应预测模型均是通过工业试验得到的非参数模型;GPC 采用的受控自回归积分滑动平均(Controlled autoregressive integrated moving average,CARIMA)预测模型和非线性MPC 经常使用的状态空间预测模型都可划分为参数模型.随着现代工业系统逐步朝着高复杂度和高集成度方向发展,利用机器学习技术建立数据驱动非参数预测模型对提高模型精度和控制品质具有重要意义.

ILMPC 预测模型的作用与MPC 相同,可以适应多种参数和非参数形式.但是ILMPC 在控制结构上与MPC 有本质区别,其二维控制结构要求预测模型同时包含时间和批次两个方向的信息.MPC算法只需考虑对象的时域动态特性,预测模型通常是基于当前时刻状态,构造控制时域内的输入向量与预测时域内的输出向量间的关系.而ILMPC 需要同时考虑对象在时域和迭代域上的动态特性,在时域预测模型的基础上进一步搭建相邻批次间的迭代关系,形成2D 预测模型.在现有ILMPC 研究中,2D 预测模型形式基本沿袭了MPC 预测模型,大致可以分为三类:2D 输入输出预测模型、2D 状态空间预测模型和2D 非线性隐式预测模型.

1.1.1 2D 输入输出预测模型

输入输出模型主要通过实际工业系统历史数据辨识得到,结构相对简单,便于直接推导输入迭代变化量和输出跟踪误差之间的关系.因此,早期的ILMPC 算法大都采用2D 输入输出预测模型.文献[36]利用平均算子建立系统干扰沿批次的迭代关系,得到了二维CARIMA 预测模型,其中控制变量仅体现沿时间方向的动态变化;文献[37]将相邻批次的系统模型作差并沿时间轴展开,形成了基于脉冲响应矩阵的2D 输入输出模型,其控制变量形式进一步体现了迭代变化规律;文献[42]通过将阶跃响应模型沿批次作差构造2D 输入输出模型,建立了控制输入增量的迭代变化关系;文献[43-45]利用CARIMA 模型沿批次的增量模型,推导了系统控制变量为输入增量迭代变化量的2D 预测模型,其中还同时包含干扰的迭代变化量;文献[46]结合了2D 脉冲响应预测模型和模糊神经网络技术,构造了非线性系统的2D 模糊神经网络输入输出预测模型.尽管采用2D 输入输出预测模型有利于降低ILMPC 控制器设计难度,但是输入输出结构无法表征复杂系统的重要状态变量信息,难以与现代控制理论和系统优化理论接轨,在算法应用和发展上都存在一定局限性.

1.1.2 2D 状态空间预测模型

状态空间方法是现代控制理论和系统优化理论的重要基础.MPC 理论体系立足于最优控制,其可行性及稳定性结论都以状态空间方法为工具.因此,在ILMPC 中采用2D 状态空间预测模型进行控制器设计,不仅对复杂批次过程控制具有指导意义,还便于利用MPC 成熟的理论体系对ILMPC 的稳定性、收敛性等系统性能进行定性分析.状态空间模型通过状态变量联立系统输入和输出,为建立跟踪误差与系统输入间的迭代关系,通常需要进行状态增广.文献[47]将分段仿射(Piecewise affine,PWA)状态模型沿批次进行增广,构建了2D Fornasini–Marchesini (FM)模型,增广后的状态变量为状态迭代变化量和输出跟踪误差,再沿时间轴基于2D FM 模型预测未来的增广状态,形成2D FM状态空间预测模型;文献[48-51]基于线性定常(Linear time invariant,LTI)系统推导以系统状态和输入变量为增广状态的状态空间模型,再通过作差的方式得到相邻批次间的迭代关系,构造了控制变量为输入信号增量迭代变化量的2D 预测模型.文献[52]针对一类具有未知输入非线性的系统,借助全局Lipschitz 连续性条件构建了显式的线性2D 状态空间预测模型,使非线性ILMPC 转化为简单的二次规划(Quadratic programming,QP)问题;文献[53]考虑一类具有未知干扰非线性的系统,建立了具有干扰不确定性的显式2D 状态空间预测模型,通过迭代计算逼近干扰量进而获得ILMPC 的近似最优解.文献[54]针对一般非线性系统,通过工作点线性化得到了显式2D 状态空间预测模型,并利用Lipschitz 条件在ILMPC 优化中实现了对线性化误差的补偿.

1.1.3 2D 非线性隐式预测模型

上述的2D 输入输出预测模型和2D 状态空间预测模型都可以归结为显式预测模型,它们采用2D 线性模型或者近似线性模型进行预测,能够直接推出未来一段时间内系统输入到系统输出的显式关系,形成的优化问题大都能够通过QP 高效求解.随着现代工业的发展,批次过程的生产规模、设备种类以及结构复杂性日益增长,简单的显式预测模型已经不足以描述批次过程的复杂动态特性.为了保证跟踪精度,直接采用较为精确的非线性模型进行隐式预测成为ILMPC 的另一重要研究方向.文献[55-56]利用神经网络模型进行隐式预测,得到的非线性优化问题通过序列二次规划(Sequential quadratic programming,SQP)、粒子群算法(Particle swarm optimization,PSO)或遗传算法(Genetic algorithm,GA)等方法进行求解;文献[57]建立了插电式混合动力汽车的2D Roesser 非线性机理模型,通过隐式预测形成非线性ILMPC 优化问题,并通过改进动态规划(Improved dynamic programming,IDP)方法进行求解.虽然2D 非线性隐式预测模型能够最大程度地保证控制精确性,但同时导致ILMPC 优化的计算复杂度大大增加.如何设计更为有效的2D 预测模型结构以实现跟踪精度和计算效率的平衡,是ILMPC 理论研究的难点之一.

1.2 控制律迭代优化

ILMPC 需要根据过去批次的过程数据沿迭代轴进行控制律更新,这通常是通过沿批次的迭代优化实现的.现有ILMPC 研究工作主要围绕着两种优化结构展开:1)将ILC 和MPC 集成为一个二维优化问题,在每个采样时刻对当前控制律进行更新;2)按顺序分别进行ILC 优化和MPC 优化,在每个批次开始前基于2D 模型求解整个批次内的ILC 控制律,再采用MPC 基于2D 预测模型进行滚动时域优化,在ILC 控制律的基础上进一步修正.通常,具有第1 种优化结构的ILMPC 算法称为整体式(Intergrated) ILMPC,具有第2 种结构的ILMPC算法称为两段式(Two-stage) ILMPC.

1.2.1 整体式ILMPC

整体式ILMPC 控制器本质是基于2D 预测模型的MPC 控制器,它借助存储的前一批次控制信息,通过最小化未来一段时间的跟踪误差获得当前批次当前时刻的控制输入迭代变化量,从而实现学习功能[37,42-44],其结构如图4 所示.整体式ILMPC的最优性、可行性及稳定性等性质可以通过MPC理论进行定性分析,优化算法的可实施性较强,同时计算负担较小.整体式ILMPC 的控制信号直接产生于MPC 控制器,一方面降低了约束处理的难度,另一方面利于与鲁棒、随机等先进控制技术结合.文献[58-59]分别针对批次系统的模型参数不确定性和干扰不确定性问题,基于2D LTI 状态空间预测模型设计了鲁棒整体式ILMPC 方法;文献[60-61]分别考虑批次过程的随机扰动和随机状态约束问题,构造了随机整体式ILMPC 策略.

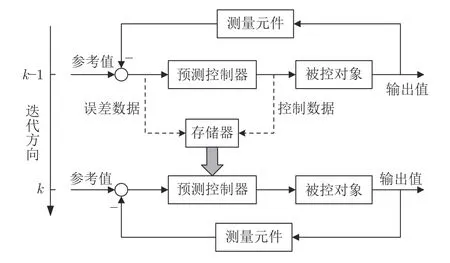
图4 整体式ILMPC 结构Fig.4 Scheme of integrated ILMPC

1.2.2 两段式ILMPC

两段式ILMPC 多基于前馈-反馈机制,通常形式为先基于存储的前一批次数据进行离线ILC 优化得到整个批次的前馈控制律,再在每个采样间隔进行滚动时域MPC 优化得到反馈控制律,其控制结构如图5 所示.这种Two-stage 优化方案将ILC功能和MPC 功能进行了分离,沿批次进行的ILC控制只处理重复性干扰,沿时域进行的MPC 控制负责抑制随机干扰.因而Two-stage ILMPC 的迭代学习进程不受随机过程信息的影响,其学习效率和收敛速度通常高于整体式ILMPC.文献[39-40]基于2D 脉冲响应预测模型,采用前馈-反馈机制构建Two-stage ILMPC 算法,通过ILC 优化和MPC优化分别产生ILC 控制量和MPC 控制量,施加于被控系统的控制作用为两者之和;文献[55]基于2D 非线性模糊神经网络模型,先独立优化ILC 控制律,再利用已知的ILC 控制量和待优化的MPC控制量推导时域隐式预测模型,通过滚动时域优化求解得到MPC 控制量.另一种典型Two-stage ILMPC保持了ILC 和MPC 功能的整体性,只根据控制目标将ILMPC 优化过程分割为两个阶段,第1 阶段抑制非重复性干扰,第2 阶段在重复性干扰下最小化跟踪误差,提高系统跟踪精度和收敛速度[62].

图5 Two-stage ILMPC 结构Fig.5 Scheme of two-stage ILMPC

综合前述的模型形式和优化结构差异,ILMPC的分类情况及各自优势、局限性如表1 所示.

表1 迭代学习模型预测控制分类Table 1 Categories of ILMPC

1.3 二维稳定性分析

ILMPC 是典型的二维控制系统,其稳定性应从迭代和时间两个维度进行分析,称为二维稳定性分析.在迭代轴方向上,ILMPC 系统的稳定性主要体现为沿批次的收敛性问题.在时间轴方向上,ILMPC的稳定性主要体现为沿时间的Lyapunov 稳定性.针对ILC 的收敛性问题,现有研究主要是通过代入控制变量显式地推导跟踪误差的迭代关系,得出系统收敛的不等式条件[63-64].这种分析方法较为简便,且能得到系统严格收敛的结论,但是不适用于无法得到显式解的带约束问题;针对MPC 的稳定性问题,基于终端约束集的控制器设计方法是保证系统Lyapunov 稳定性的最有效途径[65],通过在滚动时域优化问题中引入终端代价函数和终端约束,使得由系统优化目标函数充当的Lyapunov 函数沿时间轴递减.然而,对于具有强非线性或不确定性的系统而言,设计终端约束集仍面临很大困难.ILMPC的二维结构决定了系统的时域特性和迭代域特性互相影响,互相牵制,因此无法单独采用ILC 或MPC领域的已有方法进行收敛性或稳定性分析.此外,批次过程的强非线性、不确定性及多约束等问题导致ILMPC 的二维稳定性分析愈加困难.

1.3.1 时域Lyapunov 稳定性

2D 系统的时域性能和迭代域性能密不可分,时域稳定性是实现迭代收敛性的重要前提,在2D框架下构造具有时域稳定性的ILMPC 控制器能够为系统的实时跟踪性能提供有力保障.从MPC 稳定性理论出发,ILMPC 系统的时域Lyapunov 稳定性即指基于二维预测模型的时域优化目标函数沿时间轴的收敛问题.对于约束系统,通常要基于系统递归可行性的前提保证稳定性.利用最优解必定优于可行解的一般性结论,得到ILMPC 闭环系统的时域Lyapunov 稳定性结论.文献[37,46]通过假设在t+1 时刻控制时域内最后一个输入的迭代变化量为零,利用t时刻的最优解构造了t+1 时刻的最优解,进而根据最优解与可行解的关系,证明了目标函数在无穷时域内的有界性.文献[55-56]采用变预测时域的ILMPC 优化机制,保证每个时刻的最优解必定是下一时刻的可行解,进而实现了目标函数沿时间轴非增.文献[58-59]在时域上采用了鲁棒预测控制结构,将系统物理约束和Lyapunov 稳定性条件均转化为线性不等式约束,构造反馈控制律令系统若初始可行必递归可行.

1.3.2 迭代收敛性

ILMPC 的迭代收敛性是指:当迭代次序趋近无穷时,系统跟踪误差收敛到零或者某一常数.ILMPC的收敛性分析主要遵循两种方式:

针对无约束系统,直接求出ILMPC 优化问题的显式解,将显式解代入系统模型,推导相邻批次间跟踪误差的迭代关系,从而得到跟踪误差沿迭代轴单调收敛的不等式条件.文献[42]将ILMPC 优化问题的显式解代入阶跃响应模型,得到了相邻批次间跟踪误差向量的等式关系,再令转移矩阵的谱半径或范数小于1 得到ILMPC 系统的单调收敛条件;文献[48]基于所有批次初始状态保持不变的假设,将显式解代入Kalman 滤波器作用下的LTI 状态模型,得到ILMPC 的单调收敛条件.

针对约束系统,首先通过设计稳定预测控制器保证跟踪误差在每个批次内的收敛性或有界性,再利用批次过程的重复特性,证明跟踪误差沿批次的收敛性.文献[38]基于预测控制的稳定性分析方法推得优化目标函数值的时域有界性,进而通过前一批次末端状态和后一批次初态间的关系,证明了跟踪误差沿迭代轴收敛到零;文献[55]基于变时域预测控制目标函数的非增性质,在系统初态保持不变的前提下利用夹逼定理证明了跟踪误差沿迭代轴收敛到某一常数;文献[59]在时域上采用基于终端不变集的MPC 优化方法保证了系统跟踪误差的有界性,继而借助最优解的性质递推证明了批次内任意采样时刻跟踪误差沿迭代轴的收敛性.

2 迭代学习模型预测控制面临的挑战

迭代学习模型预测控制衍生于发展成熟的ILC和MPC 技术,具有较为完备的理论基础.但是,ILC和MPC 从控制目标、优化结构等方面存在本质区别,将两者融入到一个2D 框架下对系统的建模、优化、稳定性分析等带来了挑战.建立从建模、优化到性能分析的完整理论体系仍是批次过程ILMPC 的研究难点.同时,批次过程 “多重时变”的特点要求ILMPC 控制器对变参考轨迹、变批次长度、变模型参数等情况具有良好的适应性.如何在不影响系统2D 稳定性的前提下提高对批次过程变工况的适应性是ILMPC 控制器设计面临的又一挑战.

2.1 建模问题

建模问题一直是批次过程控制领域的研究热点[66-68].ILMPC 的时域跟踪性能和迭代域收敛特性都很大程度上依赖于模型的准确性.尽管ILC 在发展初期被定位为无模型控制系统综合方法,但在系统模型可获得的情况下利用模型构造学习律能大大提高学习效率,缩短学习过程[69-70].MPC 是一种基于模型的先进控制技术,其算法鲁棒性和稳定性都与预测模型的准确度息息相关[71-72].因此,建立精确的2D 模型对ILMPC 算法功能的实现尤为重要.实际批次过程通常具有明显的非线性特征,按模型可获取程度大致可以分为两类:第1 类是可以获取具有足够精度的机理模型的简单过程;第2 类是机理模型及辨识模型无法获取或难以用于控制的复杂过程.

2.1.1 机理建模

针对简单非线性过程,最可靠的建模方法就是根据被控系统内部机制或者物质流的传递机理建立精确的机理模型.机理模型又称白箱模型,它是基于质量平衡方程、能量平衡方程、动量平衡方程、相平衡方程以及某些物性方程、化学反应定律、电路基本定律等而获得对象或过程的数学模型.机理模型的优点是参数具有非常明确的物理意义,模型参数易于调整,具有很强的适应性.但是实际工业对象的过程特性通常无法精确表达为数学形式,并且表达式中存在大量难以确定的参数,进而影响到模型的精确性.在现今发展阶段,ILMPC 的研究工作主要面向对基础控制理论的改进和完善,因此大都直接基于对象非线性机理模型建立相应的ILMPC算法[47-54].为了在控制器设计和性能分析中运用成熟的线性系统控制理论,通常需要将非线性机理模型进行线性化,基于所得线性模型推导2D 预测模型,其中线性化误差项一般考虑为系统的不确定扰动.文献[47]将非线性机理模型进行分段线性化,并在各阶段设计不同的优化目标函数求解ILMPC控制量;文献[54]通过泰勒展开的方法对非线性机理模型进行工作点处线性化,利用Lipschitz 连续性条件在2D 预测模型中补偿线性化高阶项产生的不确定性;文献[58]将非线性注塑系统描述为具有参数不确定性的线性化系统,设计了对应的鲁棒ILMPC 策略.

2.1.2 数据驱动建模

针对复杂非线性过程,可以采用数据驱动建模的手段为ILMPC 设计提供模型支撑.批次生产过程中每时每刻都产生并储存了大量的关于过程运行和设备状态的数据,且数据量随着重复操作的进行不断累积增大.利用这些离线或在线的数据获取被控系统的动态特性是解决难建模批次过程控制问题的有效途径.以迭代轴作为参考方向,批次过程数据进行在线积累和更新;以时间轴作为参考方向,批次过程数据进行离线存储和调用.批次过程控制特有的2D 结构要求数据采集和利用也必须迭代进行.神经网络模型具有超强的非线性映射能力、泛化能力、自学习和自适应能力,在批次过程数据驱动建模方面得到了广泛关注.文献[29]基于递归神经网络对系统非线性进行重复辨识,并利用过去批次的平均建模误差对当前批次的神经网络模型进行校正;文献[55]基于批次过程数据进行模糊神经网络建模,在当前批次开始前利用前几批次存储的过程数据更新模型参数;文献[73]利用径向基函数神经网络对非线性批次过程进行迭代建模,并采用最速下降法获得网络连接权值沿迭代轴的更新方程.

随着工程数学与应用物理的深度融合以及人工智能的迅猛发展,机理建模和数据驱动建模技术都日益成熟.然而,批次过程的 “多重时变”特性对其建模过程提出了许多新要求.首先,批次过程通常用于生产高精细化产品,控制系统需时刻保持高跟踪精度,这对模型精确性提出了更高的要求.无论是机理建模方法还是数据驱动建模方法都不可避免地存在建模误差,利用迭代轴上累积的过程数据反复进行误差估计和补偿是提高系统跟踪精度的关键,也是批次过程迭代建模中的重点和难点.其次,一个完整的批次过程通常包含多个操作阶段,每个阶段的动态特性存在明显差异,如何实现多阶段精确建模和平滑切换是未来批次过程建模的重要研究方向.

2.2 优化问题

ILMPC 控制系统在每个采样间隔需要求解基于2D 预测模型的约束优化问题.当采用简单的线性模型为预测模型时,优化问题的求解效率较快,但是线性模型与实际非线性过程的失配问题会导致控制器的最优性下降.当直接采用较为准确的非线性模型作为预测模型时,尽管控制最优性会得到一定程度的提升,但是运用非线性规划求解方法会导致每个采样周期内的计算负担加重,从而造成控制效率的下降.ILMPC 优化的研究难点主要在于如何实现最优性和优化计算效率间的平衡.

2.2.1 最优性

对于基于预测模型的ILMPC 算法,提高控制最优性的首要问题是实现对模型误差的有效补偿.模型失配的程度越小,控制信号对于实际非线性批次过程的适用性就越高.文献[37]将非线性批次过程辨识为线性脉冲响应模型,在每个采样间隔利用Kalman 滤波器对预测状态进行反馈校正,使控制信号的最优性提高;文献[54]在ILMPC 算法内考虑了线性化导致的模型失配问题,利用Lipschitz连续性条件将优化目标函数表示为真实跟踪误差的上界,从而提高控制输入的最优性.

对于带不确定性的ILMPC 系统而言,鲁棒性的提高通常会导致最优性的下降.为降低系统不确定性对跟踪性能的影响,鲁棒ILMPC 的设计目标通常是保证已知范围内的所有可能干扰对系统性能指标的影响小于某一界限,或在参数不确定性包含的所有可能情况下满足鲁棒稳定性条件.文献[58]设定系统在所有可能参数下的目标函数小于某一定值,不可避免地造成了控制器的保守性,在一定程度上牺牲了最优性;文献[59]针对约束批次过程设计基于终端椭圆不变集的鲁棒ILMPC 策略,由于椭圆不变集无法实现终端域的最大化,这种保证2D 稳定性的方法必然以牺牲最优性为代价.因此,在解决系统不确定性问题时,如何定性分析系统保守性并最大限度提高最优性是一项重要研究内容.

仅从优化层面上看,ILMPC 解的最优性取决于采用的寻优方法.在线性模型下,ILMPC 优化问题通常是简单的凸优化问题,其局部最优解即是全局最优解,因此寻优方法通常不会影响解的最优性;在非线性模型下,ILMPC 优化问题通常为非凸优化问题,可能存在多个局部最优解,采用有下降参考的传统寻优方法计算量大,并容易陷入局部最优,导致解的最优性下降.针对非凸优化问题,采用PSO、GA 等启发式寻优方法能大幅提高寻至全局最优解的几率,但是这类寻优方法需要的搜索时间相对较长,只适合于采样间隔较大的慢变过程.在快变非线性批次过程中,如何达到最优性和计算效率的最佳平衡是现今ILMPC 领域的难点问题.

2.2.2 优化计算效率

在实际非线性批次过程控制中,ILMPC 的优化计算效率主要取决于两个因素:预测模型和寻优算法.降低模型复杂度和减小寻优计算负担是提高ILMPC 优化效率的两个重要途径.通过对非线性系统进行线性化获得线性预测模型,可以有效降低模型复杂度,将复杂的ILMPC 非线性规划问题转化为易于求解的线性规划问题[48].但任何降低模型复杂度的方法势必会导致模型精确度下降,因此需要同时解决模型失配问题.

在ILMPC 寻优过程中,需要从初始点开始进行多步迭代才能到达局部最优解,因此减小寻优计算量应从减少迭代步数或减小每步迭代的计算量这两个角度出发.减少迭代步数意味着加快寻优算法的收敛速度.传统寻优算法如梯度下降法、牛顿下降法和拉格朗日乘子法等都在每一步迭代中提供了下降的方向和大小参考,因此收敛速度较快;基于穷举搜索的网格法、基于随机搜索的模拟退火算法以及基于启发式搜索的PSO、GA 和蚁群算法(Ant colony optimization,ACO)的寻优过程不依赖于下降参考,参数选择和更新具有一定随机性,搜索速度较慢,需要较长的时间才能收敛到局部最优解.为提高启发式寻优算法的收敛速度,交叉算法[74]、非线性惯性权重[75]、局部聚类[76]等方案在GA、PSO 及ACO 中得到了应用,同时还出现了大量将启发式寻优算法与传统下降式寻优算法结合的研究工作,比如PSO 梯度法[77]和蒙特卡洛梯度法[78].文献[79]提出一种交替寻优算法,强制每一步的损失函数小于前一步,并设置每次寻优的最大迭代步数来减轻计算负担.在每一步计算中,减少可变参数的数量是提高计算效率的有效途径.例如在梯度下降法中减少待优化变量数量可以减少每步求导的次数和复杂程度,从而降低每步迭代的计算负担,提高整体计算效率.

对于快变非线性批次过程,现有的ILMPC 算法难以同时兼顾最优性和计算效率的问题.以寻优算法的内在机制为切入点,对ILMPC 的目标函数结构进行改造以提高寻优算法收敛速度或减小每步迭代的计算量,是发展高效ILMPC 的潜在方法.

2.3 适应性问题

批次过程 “多重时变”的特点决定了其工况会随批次或随时间变化.ILMPC 的时域滚动优化机制可以有效处理时变问题.但是经典ILMPC 理论是基于批次过程的重复特性构建的,对于沿批次的变工况问题还没有有效的解决方案.在批次生产过程中,产品类型或生产条件的改变会导致系统初始状态、参考轨迹、批次长度和模型参数不断发生变化[8].这造成ILMPC 所依赖的对象重复性前提被打破,难以发挥沿批次的学习作用.为将ILMPC 应用于实际批次过程,必须设法提高它对变初始状态、变参考轨迹、变批次长度和变模型参数等工况的适应能力.ILMPC 理论的奠基者Lee 早在2007 年就明确指出,ILMPC 研究的一个重要方向就是在变工况下实现批次间跟踪误差信息的有效转换[17].

2.3.1 变初始状态

现有的ILMPC 算法大多要求系统的迭代初态在每一批次都严格定位在期望初态上,从而实现对二维系统稳定性的严格证明.但是实际环境中的重复定位操作会导致系统存在初态偏移,且每个批次的偏移量大小都是随机的,这直接影响到系统的时域闭环稳定性和迭代域误差收敛性.ILC 通常只考虑沿批次的一维(One-dimensional,1D)无约束学习律优化,可以直接将初始状态偏差量或其范围代入系统动态方程,获得跟踪误差沿迭代轴渐近收敛的充分条件[80-82].文献[83]基于2D Roesser 模型对ILC 系统在变初始状态下的收敛性开展了理论分析,证实了必定存在一种D 型学习律使系统跟踪误差沿迭代轴渐近收敛至零.文献[84]进一步证明了PD 型学习律下ILC 系统的跟踪误差在变初始状态下必有界.在此基础上,文献[85]设计了一种自适应ILC 学习律,使系统输入同时根据离线数据和在线数据沿迭代轴进行更新,保证初始状态有界时系统跟踪误差沿迭代轴渐近收敛至零.与ILC 策略不同,ILMPC 在每个采样时刻进行滚动时域优化,初始条件的变化会对约束系统的时域稳定性产生很大影响,进而危及迭代收敛性.若初始状态在某一批次跳出被控系统吸引域,该批次内跟踪误差无法稳定到最优值.基于不稳定的前置控制经验,后续批次的跟踪精度和收敛速度都会明显降低.因此,在系统初始状态有界变化的情况下设计2D 稳定ILMPC策略十分必要.

2.3.2 变参考轨迹

在实际批次生产中,同一生产线通常需要承担不同种类、不同规格产品的生产任务,导致系统的参考轨迹会随批次发生变化,因此变参考轨迹问题一直是批次过程控制的研究热点.对于具有2D 结构的ILMPC 而言,变参考轨迹带来的影响不仅体现在迭代轴上,还会沿时间方向持续,给ILMPC 的系统性能分析带来了很大困难.相比之下,采用沿批次的一维ILC 控制,只需在迭代方向上考虑参考轨迹变化量,通过常规收敛性分析手段就可以推导出修正后的收敛性条件.因此,现有研究工作在变参考轨迹下的批次过程控制中基本都采用1D 的改进ILC 方法.文献[86]针对随机系统变轨迹跟踪问题,提出两种自适应ILC 策略,一是在控制器设计中选择当前批次的输出轨迹与下一批次的参考轨迹的差值作为新的状态变量,另一种是在每一个批次的末尾利用卡尔曼滤波器重新进行系统辨识;文献[87]针对离散非线性系统,设计模糊自适应ILC 控制器,通过不断更新模糊参数来近似变参考轨迹下的系统动态;文献[25]设计基于数据驱动的自适应ILC控制器,引入当前批次的参考轨迹作为反馈,并将过去批次的参考轨迹作为前馈以实现对变参考轨迹的跟踪.然而,1D 的ILC 算法仍存在实时抗干扰能力差、无法保证时域稳定性和收敛速度慢等弊端,亟需探索能够解决变参考轨迹跟踪控制问题的2D稳定ILMPC 策略.

2.3.3 变批次长度

经典批次过程控制假设每个批次的操作长度完全一致,并基于此前提建立学习机制.但在实际批次过程中,生产周期改变、传动装置误差以及不可控人为因素都会导致批次长度沿批次不断变化[88].变批次长度问题的关键在于对过程信息的整合.ILMPC 依靠前一批次的控制经验调整当前批次的控制信号.当相邻批次的长度不等时,必然会出现信息过剩或者信息不足的情况,需要进行信息删减或补偿保证迭代学习沿批次按步推进.近年来,已有许多学者针对批次过程控制中的变批次长度问题开展了改进的一维ILC 算法研究.为将各批次过程数据调整为相同长度,文献[88-95]设定所有缺失的误差信息为零,文献[96-98]将批次终端的误差信号延长至期望长度;为综合利用多历史批次数据,文献[88-91]引入了迭代平均算子,利用历史误差数据的平均值更新ILC 学习律;文献[94]采用高阶学习结构,根据多个历史批次误差数据和输入数据的加权值更新控制律.然而,以上方法过多使用了控制效果较差的早期批次运行数据,损失了迭代学习的最优性.对此,文献[99]提出一种基于改进复合能量函数(Composite energy function,CEF)的迭代学习机制,令控制系统在每个采样时刻只根据具有充足过程信息的最近一个批次更新学习律,实现了对新近批次的优先学习.综合来看,现有的变长度批次过程控制方法仍然在如下方面需要改进:首先,已有误差修正方法仅致力于构造等长的批次数据,而忽视了补充信息精确性对系统学习性能的影响.其次,现有的学习结构通常缺乏灵活性,无法同时适应学习数据为真实数据和补偿数据的两种情况.利用ILMPC 的时域预测功能能够在变批次长度工况下对缺失误差信息实现更为准确的补偿;针对不同数据类型需设计多种学习结构,有利于同时保证学习经验的先进性和实际性.如何在2D 框架下基于预测修正误差进行变学习模式的ILMPC 系统性能分析将是此课题的研究难点.

2.3.4 变模型参数

除了上述的初始状态、参考轨迹和批次长度等外部条件,批次过程自身的动态特性也会改变,通常体现为模型参数沿批次方向发生变化.ILMPC的二维预测和优化高度依赖系统模型的一致性,变模型参数会破坏ILMPC 时域和迭代域上的递归可行性,增大了ILMPC 二维稳定性分析的难度.目前,关于批次过程变模型参数控制的研究仍局限在ILC 领域.在模型参数已知或可估计的情况下,ILC可以通过在更新方程中直接代入变模型参数或其上界,构造自适应或鲁棒学习律提高算法适应性,并基于1D 控制结构推导出系统的显式收敛条件.文献[100-103]均采用线性高阶内部模型(High-order internal model,HOIM)描述随批次变化的系统动态特性,构造自适应ILC 策略得到系统的渐近收敛条件;文献[104-106]和文献[107]分别就变参数状态空间模型和变参数输入输出模型给出了线性系统在一般开环学习律控制下的有界条件和收敛条件;文献[108]结合广义扩展状态观测器(Generalized extended state observer,GESO),基于变参数线性状态空间模型设计二自由度闭环鲁棒ILC 策略,保证了系统跟踪误差的有界性.借鉴ILC 领域的理论成果,在ILMPC 中设计自适应和鲁棒控制结构将是处理变模型参数问题的可行方案.然而,在改进ILMPC 结构中如何确保二维递归可行并尽可能降低系统保守性仍是一个颇具难度的复杂问题.

综上,ILMPC 特有的二维控制结构给其建模、优化和稳定性都带来了巨大挑战(如图6 所示).在建模中实现多阶段迭代误差估计和补偿,在优化中实现最优性和计算效率的平衡,在稳定性分析中突破严重复性条件的桎梏,是ILMPC 理论中亟待解决的三个关键科学问题.

图6 ILMPC 的挑战Fig.6 Challenges of ILMPC

3 当前研究动态

随着控制工程界对批次过程与连续过程的界定愈加清晰,在过去20 年间迭代学习模型预测控制立足于批次过程特有的 “多重时变”性质向着更深的理论层次发展.ILMPC 二维时变框架下的建模、优化及适应性等瓶颈问题都得到了越来越多的关注,衍生了一系列优秀的阶段性成果.总体来看,ILMPC当前研究工作主要集中于两个方向:

1) 由基于机理模型的ILMPC 向基于数据模型的ILMPC 过渡.ILC 作为无模型算法,通过学习积累的历史批次数据实现对参考轨迹的高精度跟踪,实际上是一种数据驱动控制策略.而MPC 作为一种基于预测模型的优化控制算法,其时域控制效果很大程度上依赖于对系统动态模型的精确掌握.ILMPC 继承了ILC 的学习能力和MPC 的时域鲁棒性,但同时也丢失了ILC 不依赖控制对象模型的优势.当被控批次过程具有复杂非线性特征,难以建立精确机理模型时,经典ILMPC 的实施面临很大困难.随着机器学习在本世纪的井喷式发展,很多学者开始利用神经网络和强化学习等方法对ILMPC的控制结构进行转化,建立数据驱动ILMPC 算法,直接基于历史数据辨识被控系统的2D 动态特性用于时域预测,打破了模型预知这一严苛条件对ILMPC理论深化和应用拓展的束缚.

2) 对已有的ILMPC 理论进行扩展和改进,使其满足批次过程在承担不同生产任务时的特殊需求.批次过程类型众多、生产条件各异,从系统动态上可分为快时变和慢时变,从运行条件上可分为设计工况和变工况.对于快时变批次过程,需要在ILMPC 设计中关注控制器的计算效率问题,确保控制的实时性.对于存在变初始状态、变参考轨迹、变批次长度以及变模型参数等变工况扰动的批次过程,必须在ILMPC 设计中解决其引发的系统不确定性问题.近年来,ILMPC 研究领域的学者利用鲁棒、自适应、模糊、神经网络以及预测函数等先进技术,对经典ILMPC 框架进行了系统而深入的改进,针对性地解决了实际批次过程的控制需求,极大地丰富了ILMPC 的理论体系和应用场景.

3.1 数据驱动迭代学习模型预测控制

随着工业过程的生产规模及结构复杂性不断增长,许多批次过程呈现出强非线性动态特性,难以通过分析生产过程的内部机制或者物质流的传递机理获取其精确机理模型.近年来,直接利用离线数据进行优化控制的方法备受关注.在当前阶段,数据驱动迭代学习模型预测控制的研究方向大致分为两类:

1) 基于批次过程不断产生的有限时域过程数据利用神经网络沿迭代轴辨识系统的二维预测模型,再基于神经网络模型进行ILMPC 的优化求解.针对仿射型非线性批次过程,文献[56]采用控制仿射型前馈神经网络(Control affine feedforward neural network,CAFNN)对复杂非线性批次过程的重复动态特性进行迭代建模,构建基于Tube 的数据驱动ILMPC,保证在存在建模误差时系统跟踪轨迹能够收敛至参考轨迹附近的不变集内;针对非仿射型非线性批次过程,文献[73]采用了径向基(Radial basis function,RBF)神经网络对其动态特性进行辨识,并在数据驱动ILMPC 中结合CEF 实现建模误差和跟踪误差沿迭代轴的收敛.

2) 直接利用系统离线数据拟合每个批次内输入序列与输出序列间的转移矩阵,基于所得输入输出模型对未来多个批次的输出序列进行预测.文献[109-110]针对预测所需未来批次过程动态无法获得的难题,提出了一种基于不断积累的批次过程离线数据估计未来批次系统转移矩阵的新算法,成功构造了沿迭代轴的数据驱动ILMPC 策略;文献[30]考虑批次过程不确定性未知的情况,利用离线数据中包含的过程信息对未来批次的系统整体动态进行预测,消除不确定项对ILMPC 跟踪性能的影响.

3.2 高效迭代学习模型预测控制

为了适应工业机器人[111]、运载工具[112]以及快速化学反应器[113]等快动态非线性批次过程的高效率控制需求,建立计算负担低的优化控制策略也是现今ILMPC 领域的研究热点之一.通常采用的手段是将控制对象复杂的非线性动态表征为线性形式,从而实现非凸优化问题到凸优化问题的转化,降低优化求解的在线计算量.文献[114]介绍了一种即时学习(Just-in-time-learning,JITL)方法,根据输入输出数据将非线性模型沿标称轨迹线性化,建立线性时变参数模型;文献[115]直接沿参考轨迹通过泰勒展开线性化非线性模型,并在控制器设计中对线性化高阶项误差进行补偿,能够同时保证计算效率和跟踪精度.

此外,降低待优化变量维数也是提高控制效率的有效途径之一.文献[115-116]在时域控制上采用了具有特殊结构的预测函数控制,通过将待优化变量表示为一系列基函数的加权和,将维数较高的控制时域输入序列求解问题转变为维数较低的基函数权重系数序列求解问题,从而显著提高在线求解速度.

3.3 变工况迭代学习模型预测控制

变工况控制是拓展ILMPC 策略应用范围必须克服的难点问题.随着经典ILMPC 理论逐渐发展成熟,近几年来变初始条件、变参考轨迹以及变批次长度等工程实践问题受到越来越多专家学者的关注,打破经典ILMPC 要求各批次工况完全一致带来的应用桎梏已成为当前研究亟需解决的问题.

针对变初始条件问题,通常有两种解决思路.一是构造基于终端约束的ILMPC 策略[117],利用可行初始状态轨迹计算控制器的终端约束集及终端代价函数,并通过迭代逐步提高控制最优性;二是先采用固定初态的系统方程进行二维预测,再通过系统真实输出与预测输出的差值数据对控制律更新方程不断修正[118].

有关变参考轨迹的ILMPC 研究工作主要分为两个方向:经过固定期望点的变参考轨迹跟踪控制和全区间变参考轨迹跟踪控制.前一研究方向针对只需在部分采样点跟踪参考值的特定批次过程,设定系统参考轨迹为穿越各个期望点的随机轨迹,将参考轨迹跟踪问题缩小为固定点跟踪问题,通过建立点对点ILMPC 策略[51,119],保证系统对期望点的跟踪精度;后一研究方向针对参考轨迹全工作区间变化的一般情况,将其变化量表示为ILMPC 的迭代扰动项,结合鲁棒控制技术加以抑制[120-121],保证系统对整个参考轨迹的跟踪精度.

ILMPC 算法的核心思想是在滚动时域下基于前一批次的控制经验对当前批次的控制输入进行校正,其中隐含了相邻批次等长的条件.变批次长度打破了迭代学习功能依赖的基本前提,给ILMPC的2D 递归可行性和稳定性分析带来了巨大挑战.因此,变批次长度是实现ILMPC 所面临的最严峻的变工况问题,目前还没有建立与之相对应的完善的ILMPC 策略.文献[122]中讨论了一种具有预测功能的改进ILC 策略,通过建立系统输入输出预测模型,采用预测值对数据缺失的批次进行补充,将每一批次的过程数据重构为相等长度.这为在ILMPC中建立缺失信息预测补偿机制提供了参考,在此基础上继续探索变批次长度下的多学习模式和2D 性能分析方法是当今ILMPC 的理论研究新趋势.

3.4 迭代学习模型预测控制的应用动态

迭代学习模型预测控制理论正朝着无模型、强鲁棒性、强适应性的方向迅速发展,这为其在实际工业过程中的应用提供了有力支撑.截至目前,ILMPC策略已在化工[123-127]、电力[46]、供热[128]、医疗[129-131]、精密仪器[132]等多个领域取得成功应用.香港科技大学高福荣教授团队在注塑过程迭代学习模型预测控制方面开展了卓有成效的研究工作[47,50,123],实现了对注射速度的精准控制,提升了注塑产品质量和生产效益.山东科技大学王友清教授团队将ILMPC成功应用于人工胰脏智能控制[129-131],根据患者血糖动态变化实时调节胰岛素注射速度.

ILMPC 的实际应用不仅限于化学反应器、注塑机、机械手臂等典型间歇过程,也广泛渗透于发电、供热、炼钢等典型连续过程.对于动态变化具有重复性的连续过程,可以对其操作流程进行人为的周期划分,构造ILMPC 所需的 “迭代轴”.目前,基于模糊建模的ILMPC 已应用至火力发电控制[46],通过迭代学习周期性历史数据保证了对负荷指令的快速、准确跟踪.这种周期划分方法打破了迭代学习模型预测控制与连续过程间的应用屏障,ILMPC将向着应用场景多样化、应用形式灵活化的方向继续发展.

4 未来研究方向展望

作为智能制造的重要生产方式,批次过程的最终控制目标是保证各批次持续产出高质量成品,提高经济效益和社会效益.结合迭代学习模型预测控制的发展现状和批次过程控制的特殊需求,ILMPC的未来研究工作需要在解决复杂非线性建模、2D高效优化以及变工况适应性的基础上综合考虑批次生产过程的经济性问题,其途径主要包含两个层面:设计成品质量预测和控制策略、建立二维动态经济优化机制.

4.1 成品质量控制

实际批次过程通常无法直接监测产品质量,大多通过测量温度、压力等过程参量并令其跟踪预设的变化轨迹保证成品质量.因此,ILMPC 自诞生以来大都以跟踪预定轨迹为控制目标.但是各批次间配料和进程的偏差以及随机干扰都会导致既定的参考轨迹不再具有质量最优性.在ILMPC 基础上建立质量评价体系,沿时间轴同时进行系统输出序列和成品质量预测,共同优化参考轨迹跟踪性能和成品质量指标,能够实现对批次过程产品质量的实时调控.基于此思想,韩国学者Lee 等提出了早期的质量批次模型预测控制(Quality BMPC,QBMPC)策略[133-135],利用推断控制技术推导在线过程可测变量与成品质量间的相关性模型(又称软传感器),并将其与系统动态模型组合形成增广预测模型,实现对成品质量的实时预测和优化(图7).该策略在甲基丙烯酸甲酯(Methyl methacrylate,MMA)聚合反应控制中取得成功应用[136].

图7 QBMPC 结构Fig.7 Scheme of QBMPC

然而,批次过程的成品质量与过程因素及环境因素都存在着错综复杂的关系,无论是线性相关模型还是非线性回归模型都难以对其进行可靠、准确的预测,这导致QBMPC 的研究热潮仅在本世纪初昙花一现,随后便一直处于发展停滞状态.现今工业大数据及人工智能技术的迅速崛起有望为QBMPC 注入新的活力,依靠实际批次过程丰富的数据支持和神经网络强大的辨识能力,建立精确的成品质量预测模型将不再是难题,高度发展的数据驱动建模技术将使QBMPC 策略重新成为批次过程控制领域的研究热点.

4.2 动态经济性

为实现运行优化与反馈控制的有效结合[137-138],实际批次过程通常采用分层控制结构[139-140],如图8(a)所示.在实时优化层(Real-time optimization,RTO)优化经济性能指标获得最优参考轨迹,再将参考轨迹传递给动态控制层进行跟踪控制.ILMPC 策略通常应用于动态控制层,利用其迭代学习和滚动优化的特点,实现对参考轨迹的高精度稳定跟踪.然而,这种分层结构只在上层考虑了系统经济性能,丢失了动态跟踪过程中的经济信息.当被控过程出现模型失配、随机干扰等不确定性时,上层优化得到的参考轨迹不再是动态跟踪过程的经济最优轨迹.

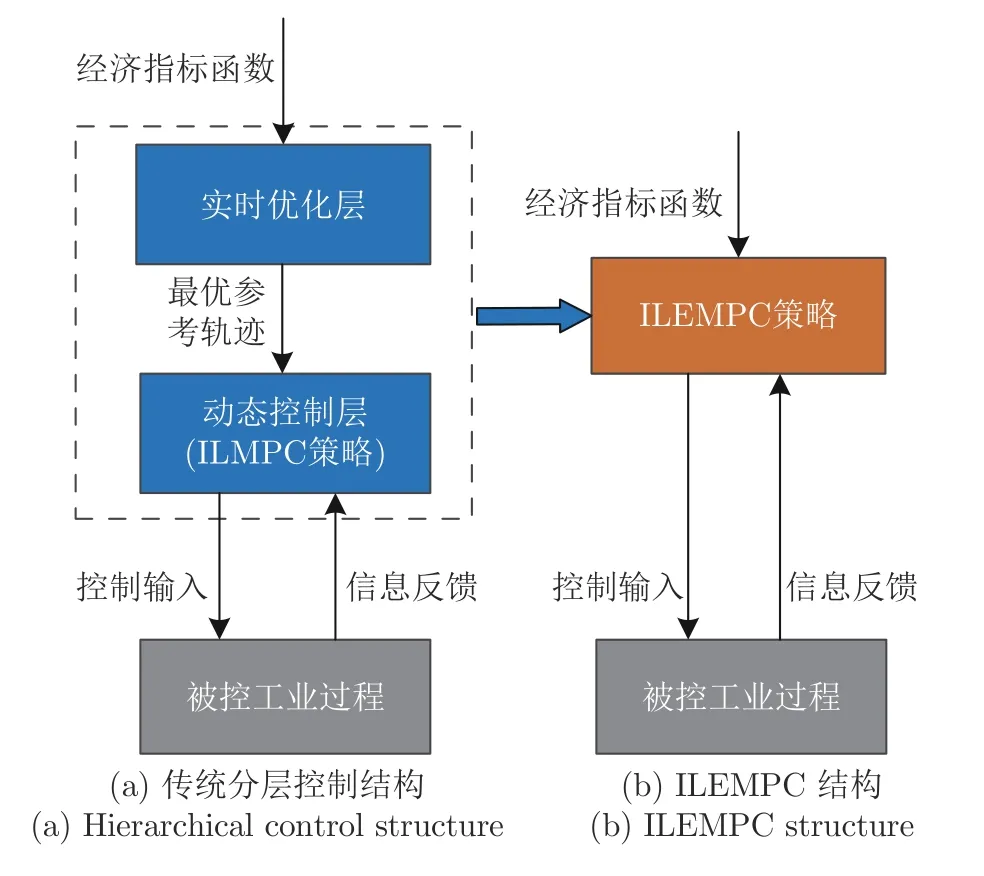
图8 传统分层控制结构与ILEMPC 结构对比Fig.8 Comparison of hierarchical control structure and ILEMPC structure

经济模型预测控制(Economic model predictive control,EMPC)将实时优化和动态控制融合在一个框架下实现,直接采用经济性能指标作为动态跟踪问题的目标函数,可以有效提高系统动态经济性能[141-143].近期,许多学者开始尝试将EMPC 理念与传统ILMPC 结合[144-147],形成了迭代学习经济模型预测控制(Iterative learning economic model predictive control,ILEMPC),它通过优化基于前次迭代数据的滚动时域经济性能指标获得每一时刻的控制输入,其结构如图8(b)所示.与经典ILMPC沿迭代轴提高跟踪精度不同,ILEMPC 沿迭代轴直接实现系统经济性能的稳步提升,目前已在间歇化学反应器[145-146]和太阳能热水器[148]控制中取得成功应用.

然而,作为一种新兴控制结构,ILEMPC 在控制性能定性分析方面还存在明显欠缺.首先,经济目标函数通常具有非二次型形式,使得传统的终端约束集方法无法保证系统的时域Lyapunov 稳定性,进而会影响迭代收敛性.如何将EMPC 的稳定性理论(如基于强耗散性的终端约束EMPC[142]、基于Lyapunov 收缩约束的双模EMPC[149])运用至二维的ILEMPC 系统是未来研究的重要内容;其次,与传统ILMPC 算法需保证跟踪误差沿迭代轴收敛至最小值不同,ILEMPC 追求的是动态经济性能沿迭代轴收敛至最优.对于各类批次过程如何设定经济目标函数并建立合理的经济性能迭代分析方案是ILEMPC 在未来发展中必须解决的关键问题.

总体来说,ILMPC 理论在过去20 多年间呈现快速发展趋势,在变工况适应性、鲁棒性、控制效率等方面已取得瞩目成绩,在经济性方面正以完善理论体系、拓宽应用范围为目标逐步深入.未来ILMPC的理论研究需紧密跟随批次过程智能化、精细化的趋势,在深化迭代学习功能的同时加强与工业大数据的交互,汲取工业控制领域与其他交叉学科的最新成果,实现在精度、灵活性、安全性、高效性等控制性能上的不断提升,并兼顾对现有2D 稳定性分析方法的拓展和突破.