基于FPSO 的电力巡检机器人的广义二型模糊逻辑控制

吴 庆 赵 涛 佃松宜 郭 锐 李胜川 方红帏 韩吉霞

高压输电线会在环境和机械的作用下出现一些故障或安全隐患,例如绝缘子老化破损、导线断股、金具氧化腐蚀等,若不能及时地排除这些问题,可能会导致重大的事故.所以高压输电线的巡检一直是供电企业的重要工作.长时间以来,我国高压输电线路的巡检工作都是通过人工完成的,这不仅耗时耗力,而且高压输电线常常会跨过高山以及江河这些人工难以到达的地方,从而出现了巡检盲区.为了使巡检工作变得更加高效和准确,我国自上世纪90 年代中期开始针对电力巡检机器人(Powerline inspection robot,PLIR)做了大量的研究[1-6],用PLIR 来代替人工进行高压输电线的巡查和维护.PLIR 具有较高的效率和可靠性,并且能轻易到达人工无法到达的巡检盲区.因此,PLIR 的研究具有重大的意义.PLIR 在高压输电线上移动时,需要面对许多的不确定性,例如风力的干扰和电线的振动,所以要对它进行控制使其达到平衡.文献[7-11]提供的方法能够对PLIR 的平衡进行控制,然而这些控制器的设计方法需要利用被控对象精确的物理模型,并且很少考虑一些不确定因素.

1975 年,Mamdani 等成功地将I 型模糊逻辑控制器(Type-1 fuzzy logic controller,T1FLC)应用在蒸汽机的控制当中[12].模糊逻辑控制器的设计不需要依赖精确的数学模型,而仅需要由专家经验总结出的模糊规则.不仅如此,模糊逻辑控制器还具有处理不确定性的能力.因此,T1FLC 得到了大量的研究,广泛运用于各种领域[13-23].广义II 型模糊逻辑控制器(General type-2 fuzzy logic controller,GT2FLC)是在T1FLC 的基础上提出来的,GT2FLC具有三维结构的隶属函数,使得控制系统处理不确定性的能力增强,所以得到广泛的关注[24-27].但同时,三维结构的隶属函数使得GT2FLC 的运算复杂度也增加了许多.区间II 型模糊控制器(Interval type-2 fuzzy logic controller,IT2FLC)相比于GT2FLC,通过牺牲一些控制性能来减少运算复杂度,也得到了广泛应用[28-29].为了简化广义II 型模糊集(General type-2 fuzzy set,GT2FS)的运算,Mendel 等[30]提出了用α平面来表示广义二型模糊集的方法,GT2FS 被分割成若干个区间二型模糊集(Interval type-2 fuzzy set,IT2FS).

在模糊逻辑控制器中,隶属函数参数的选取对整个控制系统具有极大的影响.一般情况下,隶属函数参数的选取多是依赖于经验或者实验数据,但随着控制精度要求的变高和被控系统的复杂性增加,传统的参数选取方法已经很难达到要求.尤其是在GT2FLC 中,三维结构的隶属函数使得整个控制系统无论是参数维数还是复杂度都大大增加.因此,在大量文献中,提出了用优化算法来优化隶属函数参数的方法,使得控制系统的性能更好[31-35].

粒子群优化算法(Particle swarm optimization,PSO)是应用比较广泛的一种群智能优化算法,是Eberhart 等在对鸟群捕食行为进行研究的基础上提出来的.此后,专家提出了许多改进的PSO算法,并且将其应用于不同的领域上[36-38].Shi 等[39]在基本的PSO 算法上引入了惯性权重这一概念,提出了标准PSO 算法.惯性权重在标准PSO 算法中具有平衡全局和局部寻优的能力.在此基础上,文献[40]提出了一种惯性权重线性递减的方法来改善标准PSO算法的寻优能力.然而,对于一些非线性系统,这种线性递减的惯性权重并不完全适用.文献[41]提出了一种通过模糊逻辑系统来调整惯性权重的PSO算法,使得惯性权重的调整更加合理.

本文的创新点如下:1)针对PLIR 平衡调节问题,设计了GT2FLC;2) 针对GT2FLC 系统中隶属函数参数多并且难以确定的问题,基于FPSO (Fuzzy PSO)算法来优化GT2FLC 中的隶属函数参数,从而增加GT2FLC 的性能;3) 通过仿真验证了GT2FLC相比于IT2FLC 和T1FLC 具有更好的性能和处理不确定性的能力.

1 电力巡检机器人

在本节中,我们针对PLIR 的工作原理进行介绍[1].PLIR 在高压输电线上作业时,需要通过质心调节机构的调节来保持平衡,其模型如图1 所示.PLIR关于平衡调节的动力学方程可以通过欧拉-拉格朗日方程得到,欧拉-拉格朗日方程表示为[42]

图1 PLIR 模型Fig.1 The model of PLIR

其中,ui为作用在广义坐标的外部扭矩,L可以表示为

其中,K和P分别表示机器人平衡调节模型的动能和势能,可以表示为

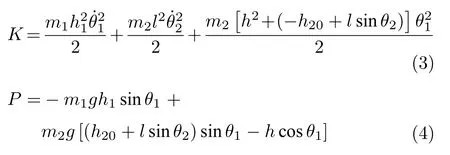
其中,θ1是PLIR 与水平轴X1的倾角,如图1 所示;θ2是执行器的杆旋转的角度;m1和m2分别为机器人主体和配重箱的质量;l为执行器的杆的长度;h是T型底座的高度;h1为机器人平衡时,配重箱的质心到高压输电线的距离;h20为电线到机器人质心的距离;g是重力加速度.以上各式中参数的值列在表1 中.通过表1,可知

表1 PLIR 对应参数值Table 1 Values of parameters for the PLI robot

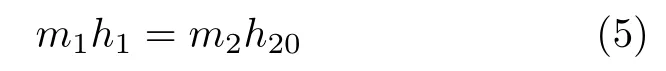
将式(5)代入到式(4)中,可得:

最终,将式(3)和式(6)代入到式(1)中,得到PLIR平衡调节的动力学方程,表示为

其中,u1是外部扰动,u2是作用在关节上的扭矩.对式(7)进行变换,并且令q3,q4]T,可得PLIR 平衡调节的状态空间模型为

在本文中,u2是GT2FLC 的控制输出,我们通过控制u2来对PLIR 的平衡进行调节,使得θ1稳定在平衡点附近.u2不能直接调节θ1,而是通过系统的耦合性来间接地调整θ1.

2 广义二型模糊逻辑系统

2.1 广义二型模糊集

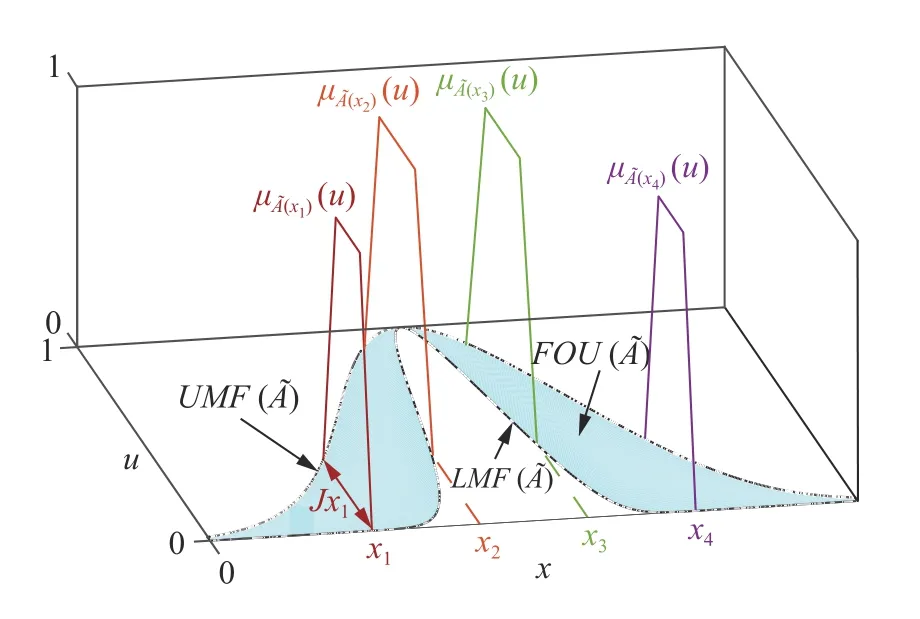
图2 广义二型模糊集Fig.2 General type-2 fuzzy set

如图3 所示,FOU 被它的上、下隶属函数所包含.其上、下隶属函数分别为,即

为了使GT2FS 的表示更加简便,文献[26]提出了GT2FS 的垂直切片表示法

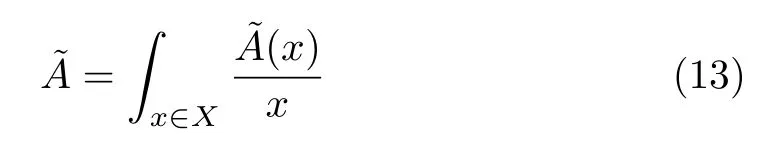
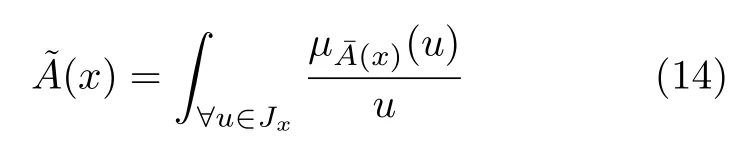
Mendel 等[30]通过α平面来表示GT2FS,(x)为的α截集,即

2.2 广义二型模糊逻辑控制器

一个GT2FLC 由模糊器、模糊推理机、规则库、降型器、解模糊器这五个部分组成.模糊器通过隶属函数,能将精确的输入量映射到模糊空间中,成为输入的GT2FS.输入的GT2FS 按照规则库中的模糊规则,在推理机中通过模糊逻辑原理得到输出的GT2FS.输出的GT2FS 经过降型器和解模糊器得到精确的输出量.

在GT2FLC 中,隶属函数的上、下隶属函数通常为三角型、高斯和梯型,次隶属函数通常为梯形、三角型和梯形.规则库中的规则一般通过专家知识建立的,一般用IF-THEN 语句来表示.在控制系统中有I个输入和N条规则,那么第n条规则具有如下的形式:

其中,(i=1,2,···,I)是与输入xi(i=1,2,···,I)对应的GT2FS,也称为前件;是GT2FLC 的后件,y是GT2FLC 的最终输出.模糊逻辑控制器中的IF-THEN规则是通过自然语言来描述的,更容易让人接受.模糊推理机一般为乘积推理机和最小推理机.对于输入向量x= (x1,x2,···,xI),经过乘积推理,得到在α平面上的激活区间为即

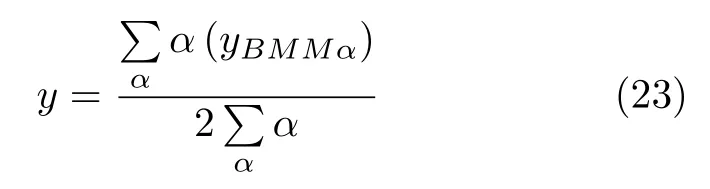
其中,α={0,1/G,···,(G-1)/G,1},G为广义二型模糊集被分割的次数,一个GT2FS 集共有G+1个α平面,y作为GT2FLC 的输出作用到被控系统中.

3 模糊粒子群优化算法原理

3.1 标准粒子群优化算法

在标准PSO 算法中,对于一个N维的优化问题而言,假设有M个粒子,每个粒子都是优化问题的一个潜在解,在t时刻,记第i个粒子的位置为Xi(t), 第i个粒子的速度为Vi(t), 而第i个粒子当前最优位置为Pbesti(t),可以表示为

其中,fit(Pbesti(t-1)) 和fit(Xi(t))为第i个粒子相对应位置的适应值.对于整个粒子群,有一个最优的位置Gbest(t),表示为

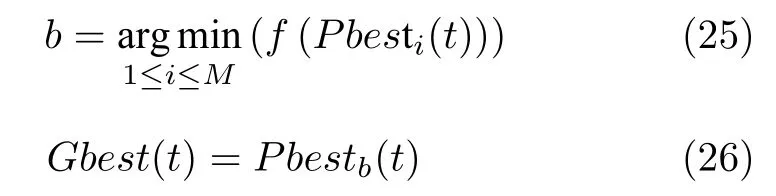
在标准PSO 中,第i个粒子通过式(12)来更新自己下一时刻的速度,即

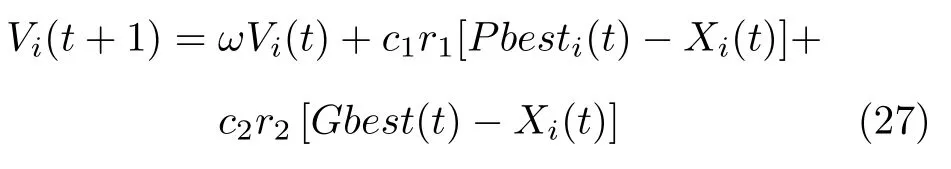
其中,ω为惯性权重,c1表示认知因子,代表粒子向自身最优值移动的加速权重;c2表示社会因子,代表粒子向全局最优值移动的加速权重;r1和r2为0到1 之间的随机变量.在粒子更新速度的时候,速度要在一定的范围内,即

其中,Vmin和Vmax为粒子速度的最小值和最大值.通过式(14),第i个粒子更新自己下一时刻的位置,即

其中,Xmin和Xmax为粒子位置的最小值和最大值.粒子需要不断地迭代来更新自己的位置,直到达到终止条件为止.终止条件一般为达到最大迭代次数或者是全局最优的适应值满足要求.

3.2 模糊粒子群算法(FPSO)

在FPSO 中,通过一个一型模糊逻辑系统(Type-1 fuzzy logic system,T1FLS)来调整惯性权重的值.在算法迭代前期,惯性权重取较大值,使得粒子具有更好的全局搜索能力,反之,在算法迭代后期,惯性权重取较小值,使得粒子具有更好的局部搜索能力.

当前迭代次数ite和全局最优位置的适应值fit(Gbest)作为模糊系统两个输入的信息,在输入之前对其进行归一化处理,即

其中,itemax为最大迭代次数;fitmax和fitmin分别为适应值的最大值和最小值.两个输入分别划分成5 个一型模糊集:NB表示负大集,NS表示负小集,ZO表示零集,PS表示正小集,PB表示正大集,它们的隶属函数如图4 和图5 所示.这个T1FLS具有25 条规则,如表2 所示.最终,惯性权重ω通过式(33)计算得到[41]

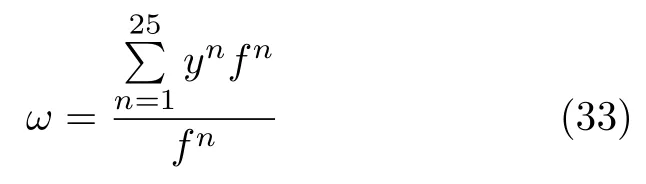
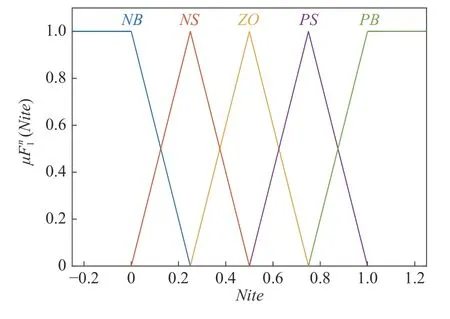
图4 Nite 对应的隶属函数Fig.4 The membership function for Nite

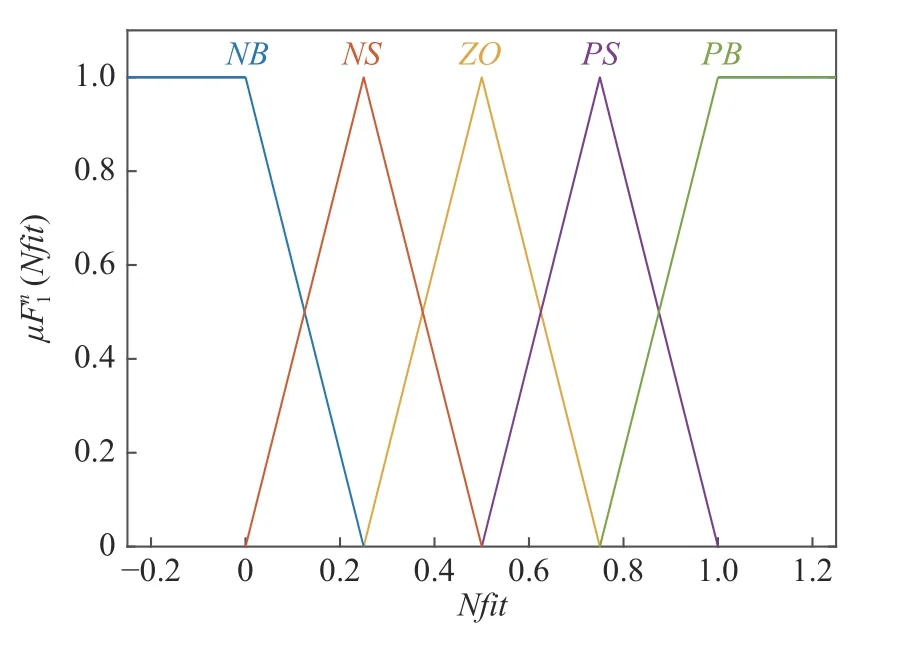
图5 Nfit 对应的隶属函数Fig.5 The membership function for Nfit

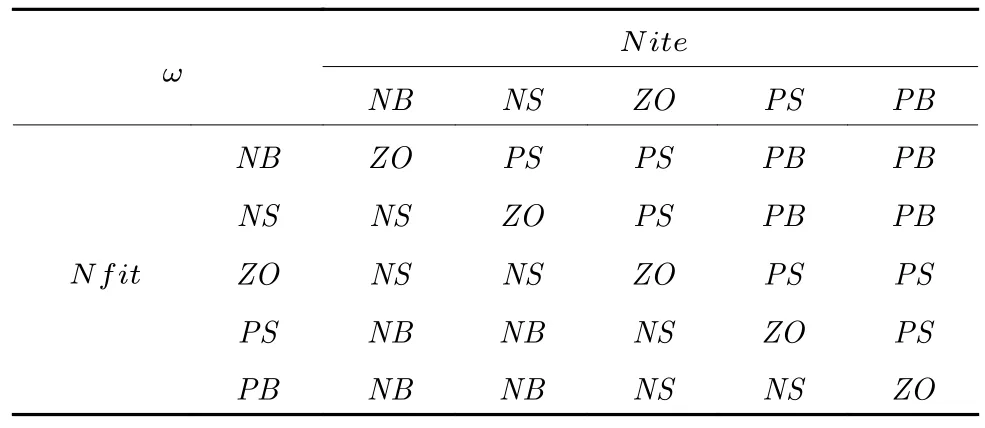
表2 FPSO 惯性权重调整模糊规则表Table 2 The rulebase of adjustment for inertia weight in FPSO

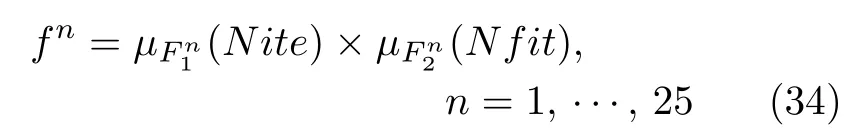
其中,yn为T1FLS 后件集;为输入对应一型模糊集的隶属度.通过T1FLS 不断地更新FPSO 中的惯性权重ω.

4 广义二型模糊控制器设计与优化

本节针对PLIR 平衡调节的问题,设计了一个GT2-FLC.基于FPSO 算法,对GT2FLC 的隶属函数参数进行优化,使得控制性能增强.图6 为电力巡检机器人的平衡控制优化的原理图.

图6 PLIR 平衡控制和优化原理图Fig.6 The diagram of balance control and optimization for the PLIR

4.1 广义二型模糊逻辑控制器设计

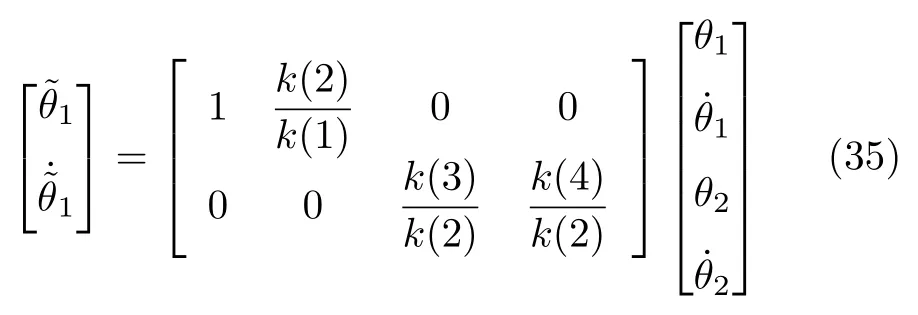
其中,k为状态反馈增益矩阵,可以通过线性二次规划的方法得到;为融合后的新的状态变量.我们将作为融合的主变量,融合后的新变量与主变量具有相同的物理意义.PLIR 的整个控制流程如图6 所示.Ke和Kec为量化因子,可以将输入量从物理论域按比例转化到模糊论域中.Ku为比例因子,可以将输出量从模糊论域转化到物理论域.

在本文中,我们用5 个GT2FS 来对输入的模糊论域进行分割,分别为负大集NB,负小集NS,零集ZO,正小集PS,正大集PB.相应的主隶属函数为高斯型.对于一个GT2FS,分别为FOU平面上的上、下隶属度值,即

其中,r为上、下隶属函数的均值;σ1和σ2分别为上、下隶属函数的标准差.次隶属函数选择为梯形,其对应α平面的次隶属度为

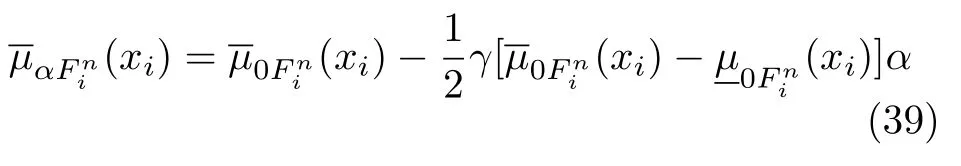
其中,γ决定次隶属函数形状的参数.特别地,当γ=0时,次隶属函数为正方型,GT2FS 转化为一个区间二型模糊集.GT2FLC 的模糊规则如表3 所示.

表3 PLIR 平衡调节模糊规则表Table 3 The rulebase of balance adjustment for the PLIR

4.2 广义二型隶属函数优化

在本文中,通过FPSO 算法对GT2FLC 的隶属函数进行优化,以得到更好的控制性能.GT2FLC的两个输入分别对应5 个GT2FS,而每个GT2FS的隶属函数需要用r,δ1,δ2,γ这4 个参数来表示,所以FPSO 中每个粒子都具有40 个维度.FPSO算法的适应度函数为平均绝对误差,即

图7 为整个FPSO 的算法流程图.最大迭代次数itemax设为1 500,种群数为50,c1和c2为1.75.本文相对文献[34],通过T1FLS 自适应动态更新PSO 算法的参数,可以搜索出更佳的GTFLC 的调节参数,从而对PLIR 实现更优控制。

图7 FPSO 算法流程图Fig.7 The flow diagram of the FPSO algorithm

5 仿真结果与分析

本节针对PLIR 平衡调节的非线性模型,运用本文所设计的GT2FLC 进行平衡控制,并且通过FPSO算法对GT2FLC 中隶属函数参数进行优化.同时,本文还考虑了外部扰动对控制效果的影响.此外,为了验证本文方法的优越性,设计了T1FLC 和IT2FLC控制PLI 机器人的平衡来与GT2FLC 作对比.最后将标准PSO 算法与FPSO 算法进行了对比.图8和图9 为GT2FLC 两个输入优化前的隶属函数的FOU,次隶属函数参数γ都为0.5.图10 和图11为GT2FLC 两个输入优化后的的隶属函数的FOU,它的γ的值分别为0.59,0.28,0.27,0.65,0.77,0.54,0.47,0.27,0.48,0.63.

图8 优化前 对应的FOUFig.8 The FOU for without optimization

图9 优化前 对应的FOUFig.9 FOU for without optimization

图10 优化后对应的FOUFig.10 The FOU for with optimization

图11 优化后对应的FOUFig.11 The FOU for with optimization

首先考虑在没有任何外部干扰的情况下,对比在FPSO 优化下的GT2FLC 与没有优化的GT2FLC的平衡控制效果,此外,还与FPSO 优化下的IT2FLC和T1FLC 平衡控制效果进行了对比.初始状态图12 和图13 为PLIR 四个状态的响应,可以看出,经过FPSO 优化后的GT2FLC能使PLIR中的θ1到达平衡点位置后具有更小的超调,并且振荡更小.除此之外,优化后的GT2FLC也比同样经过优化的IT2FLC 和T1FLC 具有更好的性能.

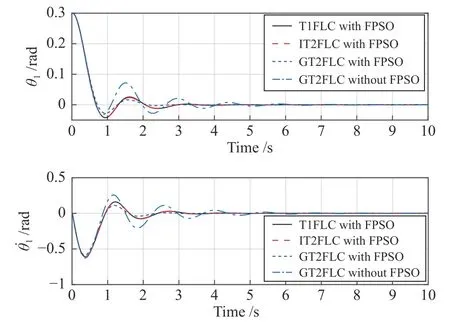
图12 无干扰下 θ1 和 的响应Fig.12 Responses of θ1 and without disturbance

图13 无干扰下 θ2 和 的响应Fig.13 Responses of θ2 and without disturbance

接下来考虑在有干扰情况下,将几种控制器的控制效果作对比.当PLIR 机器人达到平衡时,遇到一个外部干扰u1=30 N,干扰持续0.5 s.图14和图15为在干扰下PLIR 的四个状态的响应.显然,两个GT2FLC 相比于T1FLC 和IT2FLC 具有更好的处理不确定性的能力.TIFLC 在遇到干扰后回到平衡位置速度最慢.

图14 有干扰下 θ1 和的响应Fig.14 Responses of θ1 and with disturbances

图15 有干扰下 θ2 和 的响应Fig.15 Responses of θ2 and with disturbances

为了验真FPSO 算法的优越性,我们用标准PSO算法和FPSO 算法分别对几种控制器进行30 次优化.将两种优化算法优化后的控制器分别对两种情况下的PLIR 机器人进行平衡控制,因为θ1代表PLIR与水平轴的夹角,所以我们通过评价函数对θ1进行计算来量化控制效果.评价函数分别为平方误差积分(Integral square error,ISE)、误差绝对值积分(Integral absolute error,IAE)、时间乘以误差绝对值积分(Integral time absolute error,ITAE)

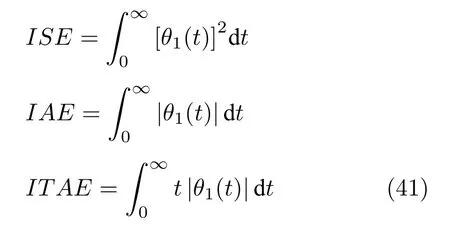
评价指标越小表明控制器具有越好的性能.表4为几种控制器在无干扰情况下的评价指标的均值,表5 为几种控制器在有外部干扰情况下的评价指标的均值.可以看出,在相同控制器之间进行对比,FPSO 优化后的评价指标要比标准PSO 优化的评价指标更小.

表4 无干扰下平均评价指标Table 4 Average evaluation index without disturbance

表5 有干扰下平均评价指标Table 5 Average evaluation index with disturbances

6 结束语

本文针对PLIR 平衡调节问题,设计了一个GT2-FLC,并且通过FPSO 算法优化了GT2FLC 中的隶属函数参数.仿真结果表明,GT2FLC 经过FPSO算法的优化,使PLIR 更快地到达稳定位置,并且具有更小的超调.通过与IT2FLC 和T1FLC 的对比表明,本文所设计的GT2FLC 有更好的控制效果.在标准PSO 与FPSO 的对比中,可以看出经过改进后的FSO具有更好寻优能力.在GT2FLC中,隶属函数对控制性能具有很大的影响,GT2FS三维结构的隶属函数相比于IT2FS 与T1FS 有更多的自由度,使得GT2FLC 具有比T1FLC 和IT2FLC更大潜力.在未来的工作中,主要是通过三维仿真平台对本文的算法进行仿真,以验证本文所提算法的有效性。