基于多阶运动参量的四旋翼无人机识别方法

刘孙相与 李贵涛 詹亚锋 高 鹏

“低慢小”(飞行高度低、飞行速度慢、目标小)目标以其难以被探测、便于隐藏、适用场景广泛的特点,一直以来都是军事以及科研领域中的研究重点[1-4],其中 “低慢小”目标的探测识别更是相关课题中的核心和基础问题.近年来,四旋翼无人机为代表的新兴 “低慢小”飞行器因其成本低廉、操纵简单、难以被发现的特点,在航拍、探测、检测等多个领域被广泛应用.但随之而来也带来诸多安全隐患,如成都机场无人机 “黑飞”逼停客机、默克尔总理竞选会无人机潜入、叙利亚自制 “武装无人机”自杀式袭击等.这些已有公共安全事件说明无序飞行的 “低慢小”无人机已经严重威胁到社会秩序和公共安全.

近年来,人工智能和计算机视觉的发展,使得基于图像/视频的小目标检测与识别方法的性能有了较大的提升,成为研究此类问题的新手段[5-8].相比于以往基于声谱特征[3-4]、光谱特征[5-6]、射频和雷达[1,9-10]等方法,基于机器视觉的方法具备系统简单、硬件体积小、场景普适性强、探测距离远、识别粒度细等优点.基于机器视觉的 “低慢小”目标识别方法主要包括表观特征方法[11-26]、运动特征方法[27-35]以及混合方法[15,36-45].

基于表观特征的方法,如部件模型(Discriminatively-trained part model)[11]、Faster RCNN 神经网络[12]、SSD(Single shot multibox detector)神经网络[26]、积分通道(Integral channel)[13]等在许多常见目标以及一些小目标识别任务中显著提升了识别精度.Zahangir 等[24]改进循环卷积神经网络,融合Inception-V4 和残差网络结构,形成IRRCNN识别网络完成对输入图像的目标识别,在多个数据集上,如 CIFAR-10、CIFAR-100、TinyImageNet-200 以及CU3D-100,达到最佳识别精度.对于无人机目标来说,Schumann 等[17-18]提出了采用Faster RCNN网络进行识别的方法,并在其建立的数据集上进行训练,识别鸟类和无人机两类目标,在AVSS2017[23]测试集上取得了最高精度;Saqib 等[25]测试了不同结构的卷积神经,得出采用VGG16结构的Fasster-RCNN 神经网络具备最高识别精度;Aker 等[14]提出了将鸟类和无人机在不同背景下合成的数据集生成方法,用以训练无人机识别神经网络;Wu 等[28]提出通过将显著性方法引入至卡尔曼滤波器,完成对运动小目标的跟踪和定位,该方法对于四旋翼无人机的跟踪也具有较高精度.Carrio 等[20-21]在深度图中采用神经网络方法完成四旋翼无人机的识别,并在Airsim 飞行仿真软件中建立深度图数据集,用以训练识别方法,得到了其数据集上的最优识别精度.但该方法对目标的表观和运动特征均未直接使用,对于常见的识别场景适用性较差、识别精度相对较低.

基于运动特征的方法,主要分为两类,一类是基于背景减除;另一类是基于流方法.背景减除类方法的前提是假设相机不动或者仅有很小移动.通过对背景进行建模,从而达到仅在图像中留下前景目标的目的,此类方法[27,30-31]计算复杂度低、适用场景广泛,但仅能在背景简单下具备足够精度;流方法[6,32-34]依赖于流向量的计算,其适用于多目标场景、在复杂场景中也具备较高召回率,但对于识别任务来说,针对小目标或者复杂场景计算精度不足,计算复杂度和虚景率也较高.基于深度网络的光流提取方法提高了光流向量的计算精度,Dosovitskiy 等[33-34]提出FlowNet、FlowNet2.0 等结构,采用U-Net 架构,并融合多种网络结构,取得了目前最优光流提取性能.

融合运动以及表观特征的方法,目前多以深度网络 (Deep neural network,DNN)为基础框架,主要包括卷积神经网络 (Convolutional neural network,CNN)[37-41]和循环神经网络(Recurrent neural network,RNN)[42-43,46].T-CNN (Tublet CNN)[37]借用Faster RCNN 中RPN (Region proposal network)的高效结构,提出Tubelet 结构关联上下文特征,即通过光流法得到的在连续多帧中同一目标识别矩形框,并采用LSTM (Long short-term memory)[46]网络作为分类器完成分类.此方法能够抑制虚景目标,提升正样本的识别概率,但对于小目标召回率较低.DFF (Deep feature flow)[38]使用基于深度网络框架的FlowNet[33]方法提取光流特征,通过目标运动过程联系上下帧并筛选关键帧,节省了对非关键帧特征提取和识别的计算过程.Zhu 等[39]在像素级 (Pixel-level)融合通过FlowNet计算得到的光流区域的特征图,融合相邻多个特征图并输入到最终的判别网络中.与以上两个工作类似,本文方法也采用了光流法提取上下帧目标的运动过程,但并非综合运动过程中变化的外观特征,而是重建目标运动过程中的运动学参数.Bertasius 等[40]引入可变尺寸卷积 (Deformable convolution)对上下帧中目标运动引入的额外特征进行融合,而非采用光流联系上下帧.Luo 等[41]融合区域级特征(Proposal-level)而非像素级,其考虑候选区域内的语义特征,并综合相邻两帧语义特征、位置特征以及时间特征完成识别,取得了ImageNet VID[47]数据集中的最优性能.以上方法主要以Faster RCNN或RPN 为主要框架,近年来,以RNN 为框架的方法[41-44]在计算效率以及精度上也达到了较高水平,Xiao 等[42]利用ConvGRU结构融合时空特征,在ImageNet VID 数据集上,曾取得最优性能.Chen等[43]提出的基于ConvLSTM[44]和SSD (Single shot multibox detector)[26]网络结构,并融合注意力机制的方法,综合了多尺度的特征 (像素级和目标级),是目前综合计算速度与精度的高性能方法.本文方法也采用了基于RNN 结构的GRU (Gated recurrent unit)网络[43-44]作为分类器,但其输入为运动参量,而非图像.

特别地,对于 “低慢小”目标的混合识别方法,Lv 等[29]通过融合时空两种特征,完成了对弱小飞行器目标的探测;Shi 等[36]提出采用改进粒子滤波的方法探测低速飞行小目标,对于海面背景的飞行器目标来说,其相较与分型方法 (Fractal-based)和三特征方法 (Tri-feature-based)性能更佳.对于无人机目标来说,Farhadi 等[23]提出将前景检测结合目标形状进行识别的方法,在综合指标上,取得了AVSS2017[14,16,23]方法中第二高精度的性能.Sapkota 等[19]提出利用级联检测的思路,识别无人机后利用混合高斯概率假设密度滤波器跟踪无人机飞行轨迹,实现了两架无人机的实时跟踪.Rozantsev等[15]融合了表观特征以及运动特征,利用目标运动补偿来提高识别精度,即通过决策树和卷积神经网络估计目标在像平面的运动,进而采用卷积神经网络识别获得的图像立方体中的目标.该方法在其提供的测试集中取得了目前最优结果.但该方法未考虑多干扰目标和多类别的识别,难以应用在实际场景中.

相较于以往工作,与文献[15]相似,本文方法也基于融合表观和运动特征的思想,采用了文献[6,32-36]中所涉及到的光流法进行运动特征提取,并利用文献[42-43,46]等工作中提及的GRU 网络完成目标判别.但不同的是本文从运动学角度直接提取目标的运动特征,而非仅采用运动特征辅助串联前后帧表观特征的提取.并且本文采取决策融合的方式而非特征融合,这样能针对性地充分考虑运动和表观两个不同维度的特征.从算法适用条件及精度来说,以往工作都在一定程度上实现了无人机的跟踪和目标的识别,但基本都要求单一纯净背景下的单目标作为前提条件.而对于低空干扰目标较多、背景较复杂这一现实约束,这些方法均无法做到高精度识别.此外,以往工作均采用对常见物体识别使用的通用框架,并未意识到无人机 “低慢小”的特殊之处,也未对此特点加以利用.在构建相关实验数据集时,也未考虑无人机的特征,涵盖的飞行场景较少.

本文以典型四旋翼无人机探测为目标,综合其表观和运动特征,提出了一种基于目标多阶运动参量的识别方法 (Multi-order kinematic parameters based detection method,MoKiP).本文中,多阶运动参量是指一个运动参数的集合,包括零阶运动参量(表观特征),一阶运动参量(速度、角速度),二阶运动参量(加速度、角加速度),以及更高阶的运动参量.

如图1 所示,该方法的核心思想如下:首先提取并跟踪运动候选区域,并估计候选区域的深度信息,然后计算出相应的非零阶运动参量,之后,采用梯度提升决策树以及记忆神经网络完成基于运动特征的短期和长期识别.同步地,采用Faster RCNN[12]深度网络对零阶运动参量(表观特征)进行识别.最后,将零阶和非零阶两部分识别结果,按照识别概率加权平均融合,得到最终的判别结果和类别概率.

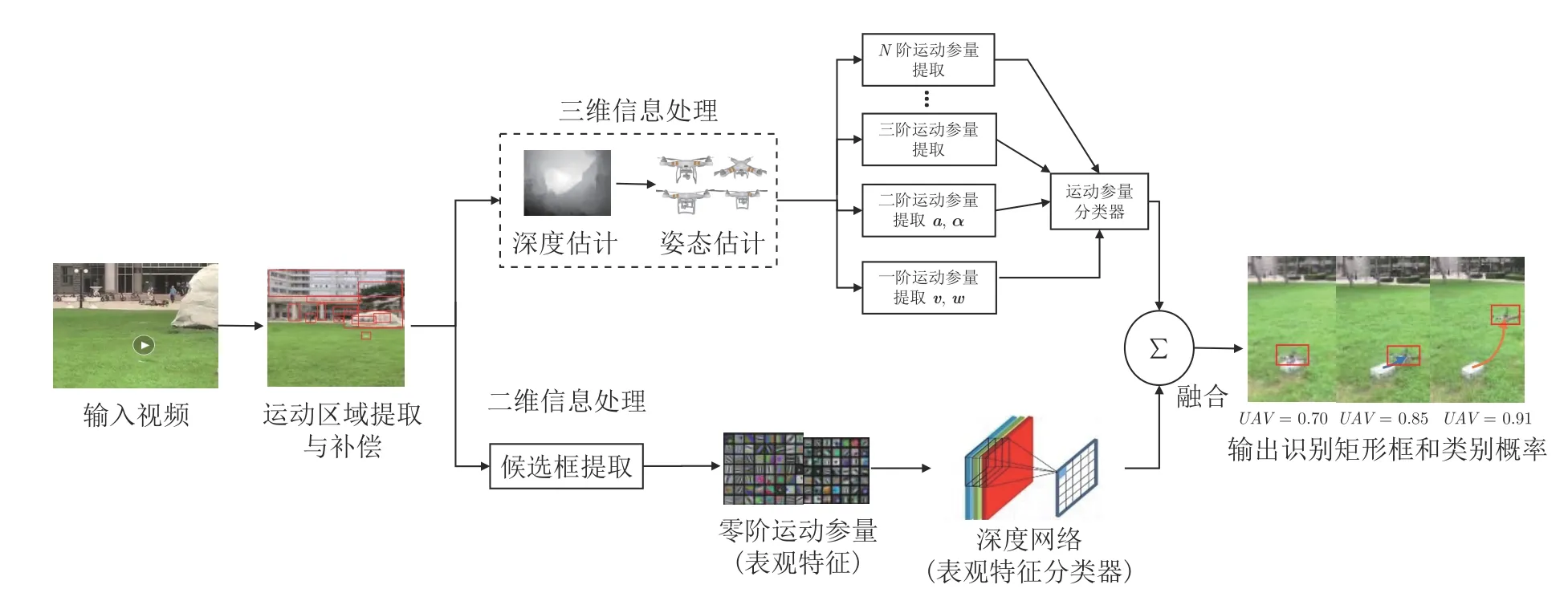
图1 本方法整体流程图Fig.1 The overall flowchart of our method

实验证明,在目标像素较少、背景复杂以及干扰目标较多的情况下,相比于以往方法,本文提出的方法具有更高的识别精度.此外,通过灵敏度分析,本文进一步定量分析了各阶运动参量对识别精度的贡献程度,并发现二阶参量、重力方向参量是识别过程中影响较大的重要特征.

本文的主要贡献如下:

1)提出基于多阶运动参量的 “低慢小”识别方法.较好地处理了低空、复杂背景以及多目标场景下的识别问题.

2)发现了二阶运动参量以及沿重力方向的运动参量最能反映无人机与其他干扰目标在运动特征上的差异.

3)建立了多尺度无人机数据集.包含四旋翼无人机以及行人、车辆、鸟类等干扰目标的相关数据.并为其它干扰目标进行了数据采集和标定.

1 基于多阶运动参量的无人机识别方法

1.1 总体识别流程

本文在充分挖掘无人机运动信息的基础上,提出了一种基于多阶运动参量判别融合的无人机识别方法.其输入为场景的视频片段,输出为目标的识别矩形框和所属类别概率.该方法的流程如图1 所示:首先,利用ViBe+(Visual background extractor)[30]法,提取候选运动区域.然后,分别提取无人机的表观特征和运动特征,并分别根据这两类特征识别目标类别.最后,融合两个识别结果,给出最终识别的概率.

本文中定义物体的表观特征为零阶运动参量.其处理流程如图1 下半分支所示.利用Faster RCNN 深度神经网络,根据输入视频获得目标图像特征的识别矩形框和类别概率.图1 上半分支根据目标运动特征,即非零阶运动参量进行识别.该方法首先利用ViBe+法提取运动区域,其次,通过单目估计或物理测量等方法获得运动目标区域深度值.之后,根据深度图,估计运动区域内目标的零阶以上运动参量.然后,训练得到基于运动参量的GBDT决策树 (Gradient boosting decision tree)[48]和GRU (Gated recurrent unit)[46]记忆网络,分别实现对无人机的短时和长期的识别,并得出识别矩形框和所属类别概率.最后,将零阶和非零阶两部分识别结果,按照识别概率进行加权平均融合,得到最终结果和类别概率.

1.2 基于零阶运动参量的特征提取方法

零阶运动参量代表了目标 “不动”时所传递的信息,也就是其表观特征.以往工作中已经有了很多成熟有效的算法[11-13,26,46,49]进行表观特征提取,本文采用了以提取区域候选网络 (Region proposal network,RPN)为前端的两阶段Faster RCNN[12]神经网络.其在Pascal VOC[11]、ImageNet[47]等公开数据集中,均取得了最优性能 (State-of-the-art,SOTA).本文使用基于Resnet101[49]框架的Faster RCNN 网络,以获得目标识别的矩形框,以及5 类目标的识别概率.所采用的Resnet101 结构在ImageNet 数据集中预训练,并在本文多尺度无人机数据集 (Multi-scale UAV dataset,MUD)中参数细调 (Fine-tune).对于RPN 网络的训练,尺度参数设置为5 (2,4,8,16,32),3 个矩形框比例分别设为(0.5,1,2),总共15 个锚 (Anchors).在训练时,使正负样本数比例达到1:1.

在使用本文融合方法进行识别时,采用按训练识别概率加权[50]的方法,融合基于零阶与下文非零阶的识别结果,得到最终判别结果.具体来说,对于某一候选区域、某一类别的识别概率为分别采用零阶、非零阶运动参量方法识别得到的概率按测试集(在调参时按训练集)准确率加权求和的结果.若某一区域仅被零阶或非零阶中的一种方法所识别,则另一方法识别概率按零计算.

1.3 基于非零阶运动参量的特征提取方法

图2 给出了基于非零阶运动参量识别的详细流程,其输入为运动区域的图像流,输出为识别得到的识别矩形框与类别概率.以下各小结将根据运动特征识别的流程,依次阐述识别过程中的各个环节.主要包括目标运动区域提取、运动参数辨识、候选目标姿态测量、目标类别与运动参量的条件概率密度函数估计等.其中,参数辨识过程包括了相机运动的识别与补偿、水平面估计、深度估计等.对于条件概率密度函数的估计,本文利用梯度提升树完成相邻几帧的短时识别;利用GRU 记忆网络完成长时识别.在描述每一步处理的过程中,本文也将分析每个环节对最终识别效果的影响.

图2 基于多阶运动参量的目标识别方法流程图(MoKiP)Fig.2 Flowchart of multi-order kinematic parameters based detection method (MoKiP)

1.3.1 运动目标区域提取

疑似目标区域提取是本文所述识别方法的第1 步.在无人机识别问题中,目标所处的环境复杂多样,反映到图像,则会导致目标图像具有背景变化剧烈、多目标的特点.所以本文采用目前在多数常见场景都具备高召回率的ViBe 改进算法ViBe+[30]提取运动区域.其主要流程为:

1)背景初始化建模

给每一个像素点建立像素样本集.一般为从该点邻域以及过去时刻邻域像素中随机选取20 个点.邻域点即与该像素点相邻的8 个像素点.

2)前景检测

设置闪烁阈值以及更新因子.对于本时刻某点邻域内,若邻域点中像素值大于闪烁阈值的点的个数超过更新因子,则将该点设为前景点.

3)背景模型更新

某像素点只有被分为背景样本时,才能被包含在背景模型中,而前景点不能被用于构成背景模型.更新过程遵循时间和空间的随机性.空间随机性是更新的像素随机替代样本中任意像素,时间随机性是指当一个像素点被判定为背景时,它有 1/rate的概率更新背景模型.rate为更新因子,根据更新需要设置为1、5 或者16 等值,由于本文所涉及的场景背景有较快速变化,此处设置rate=5;如果某个像素点连续N次被检测为前景,则将其更新为背景点,一个像素点在本时刻不被更新的概率为(N-1)/N,在本文设置N=15.

另外,加入关于Ghost 区域的消除、除去不完整目标、自适应阈值等改进,其余参数详见文献[30].通过Vibe+方法提取的运动区域如图3 示意.

Movi表示提取出的运动区域(目标包络线以内);如图3 所示,采用一个能够包含此区域的最小矩形包围框,作为待检测目标区域候选矩形框.则候选窗口可以用式(1)表示:

图3 运动区域提取示意图Fig.3 An illustration of the extracted motion ROI(Region of interest)

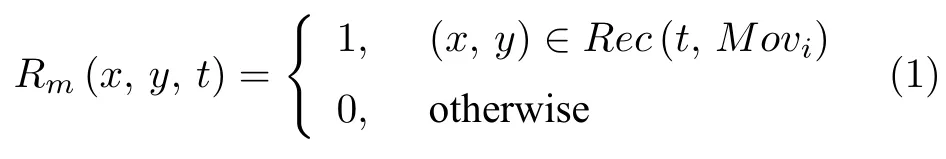
其中,Rec(t,Movi)表示在t时刻包括运动区域i的最小矩形框;Rm为最小矩形框所形成的二值掩码矩阵.

1.3.2 运动参量辨识

快速且精确的运动参量辨识过程是本文提出方法的核心.如不加特殊说明,本文中所有运动参量均以地面坐标系为基准(X轴与图像平面坐标系中u轴方向保持一致,Z轴铅垂向上,Y与X和Z轴构成的平面垂直,构成右手坐标系),并根据其相机坐标系下的测量分量,通过水平面估计矩阵转换至地面坐标系下对应的分量.本节所述的一阶和二阶运动参量包括三轴平动速度、三轴角速度,以及对应的加速度、角加速度.三阶及三阶以上的参量较为特殊,将在第3.6 节中单独阐述.

本文假设相机始终保持静止.对于场景中的运动目标,首先获取目标运动区域内的深度值;然后,进行水平面的矫正;最后,采用差分估计提取得到目标的运动参量.

1)运动区域深度图

目标在图像平面内的运动和其对应的深度值共同决定了目标在三维空间内的真实运动规律.因此需要首先获取目标的深度信息.

目前获得深度图的手段有激光测距、立体视觉、图像估计等方法.根据不同识别场景的需求,应选取不同方法获得深度图,在获得的深度图中,每个像素代表该图像位置的深度值,此外还可能包含深度测量的置信度或误差等信息.对于常见的识别场景,从图像中直接估计深度信息的方法具备更强的适用性,所以本文选择采用目前单目深度估计方法中具备最佳精度的DORN (Deep ordinal regression network)[51]方法.

2)水平面方向估计

考虑到相机仍存在旋转,为了更加准确的估计运动参量,需要补偿相机旋转对参量估计的影响,修正深度方向至与相机所在世界坐标系保持一致.本文采用改进隐马尔科夫[52]方法进行估计,获得水平面旋转修正矩阵.该方法能够在多种场景下鲁棒地估计水平面方向,并具有相比于以往文献较高的精度.对于本文的识别问题,当探测场景为低空场景时,直接采用此方法进行水平面修正.而当探测场景为对空场景时,场景中无地平线作为参考,因此无法获取估计所需的特征.此情况下,可近似认为深度方向即为海拔高度方向.

3)一阶和二阶运动参量提取

根据以上章节获得的候选区域逐点深度信息,及其在像平面内的轨迹,本节将从这些信息中提取运动区域内目标的特征点,然后计算其一阶和二阶运动参量.

首先,本方法采用具有快速和鲁棒特性的ORB (Oriented fast and rotated brief)[53]算法提取Movi内的目标特征点.设当前第t帧中运动区域Movi内提取的第i个特征点 (ORB 算法具备足够检出速度和特征点鲁棒性) 在图像坐标系下为深度为, 其在t-1 帧,对应的匹配点为其深度为其在t+1帧对应的匹配点为深度为相机焦距为f,帧率为F,总共特征点个数为N,根据相机几何,则此时刻第i个目标特征点在三维空间中的坐标为,相机坐标系下坐标为.

运动区域Movi内待提取的运动参数ρ=(v,a,ω,α),分别代表目标运动的平动速度,平动加速度,角速度,角加速度矢量,即目标作为刚体运动时的运动学参数.为估计这些运动参量,第1 步是获得目标的位移向量以及旋转矩阵

若运动区域内相邻帧匹配特征点N≥4 时,采用EPnP (Efficient perspective n point)[54]方法,则空间中点其图像中匹配点为ui=(xi,yi), 四个控制点的坐标为cj,j=1,···,4,世界坐标系下的任意三维点可表示为

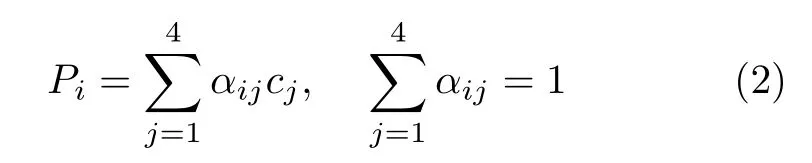
通过齐次质心坐标αij,将上式可以写成齐次坐标形式

则对于任意匹配的空间三维点Pi,相机投影模型可重写为如下形式

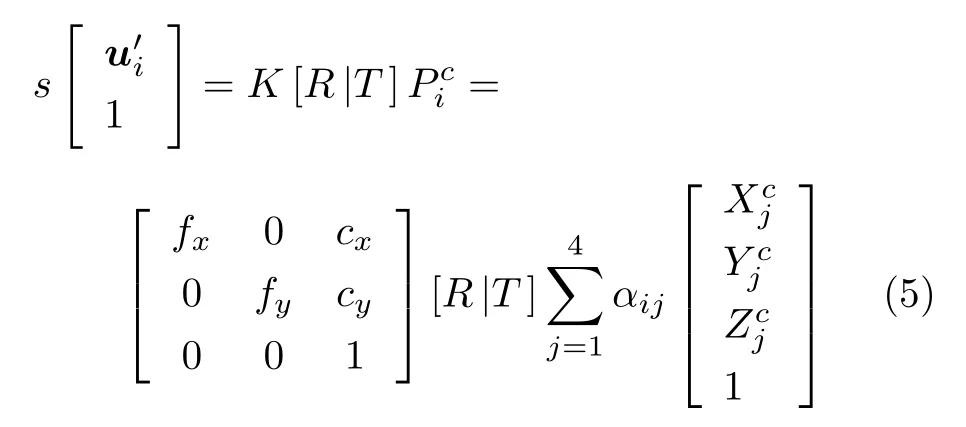
根据相机投影模型(5),在不考虑外参数矩阵[R|T]的情况下,求解控制点在相机坐标系下的坐标,消去式(5)中最后一行.

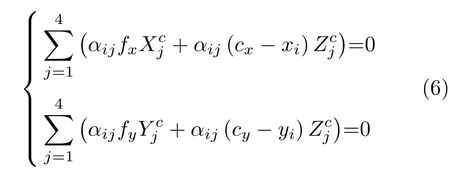
其中除相机内参数fx、fy、cx、cy,以及已知匹配点坐标ui=(xi,yi) 外,4 个控制点共计12 个未知参数.根据中间变量法以及近似线性化的约束,将所有N个特征点作为输入,可以解得P0,得到质心坐标.于是,问题就简化为点匹配的ICP (Iterative closest point)问题,即将质心偏移矩阵SVD 分解,得到本时刻的旋转和平移矩阵 [Rt|T t],详细计算过程参见文献[54].

根据所获得的平移和旋转矩阵,则本运动区域在当前时刻的速度vt,沿第1.3.2 节约定的X、Y、Z轴三方向的分量分别为则

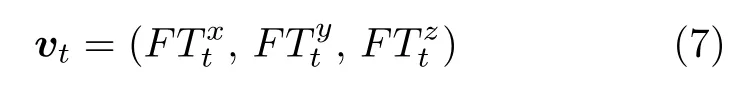
对于已得到的速度向量,根据中心差分,设at三方向分量为则

由式(2)～(8),本文获得了候选目标的平动参数.

对于转动参量,由罗德里格斯变换,相邻两帧的旋转角度φ为

其中, tr(Rt)为矩阵Rt的迹.则根据式(9),转轴u=(ux,uy,uz)(单位向量)的反对称矩阵 [u]x为

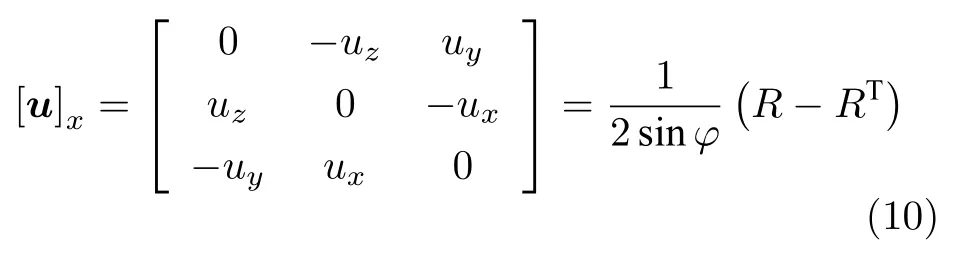
其中,RT为R的转置.则角速度ωt可表示为

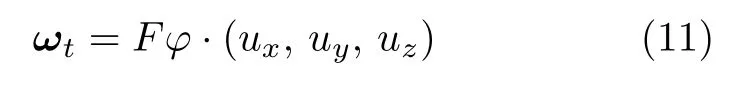
基于此,采用中心差分,角加速度可表示为

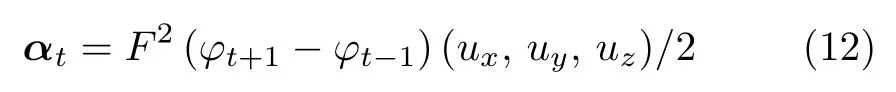
至此就得到了目标所有的一阶与二阶运动参量.

1.3.3 运动参量决策树

至此,用于描述物体运动特征的一阶与二阶运动参量都已获得.在本节中,本文将基于运动参量建立无人机识别模型.由于参量数量较多且相互关系复杂,直接估计每一类别关于运动参量的后验概率较为困难(其中,参数分别为目标的速度、加速度、角速度以及角加速度).因此,本文方法将识别过程分解为短期和长期两个步骤.短期预测以快速检测为目的,对于输入视频完成实时处理,适用于实时性要求较高的场景.长期识别以高精度检测为目的,当在视频时长足够的情况下,确保算法具备较高的识别精度.

其中,梯度提升树(Gradient boosting decision tree,GBDT)完成短时识别并筛选关键运动参量.而具有更高识别精度的LSTM 网络则被用来完成长期识别.该方式能够根据需求选择不同的针对性方法,在实时性和高精度之间保持较好的平衡.

当前帧以及相邻前两帧的所有运动学参数共计36 个,以这些参数作为分量建立描述这些参数的GBDT 分类树.选择CART 树作为弱分类器,采用交叉熵作为损失函数

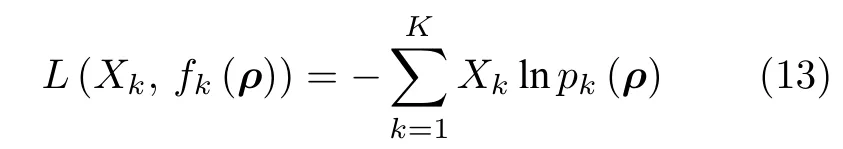
其中,Xk={0,1}表示是否属于第k类,1 表示是,0表示否,k=1,2,···,K为总共类别数(本文类别包含四旋翼无人机、行人、车辆、鸟类、以及其他,共5 类,则K=5 ),ρ=(v,a,ω,α) 为所采用的运动参数.pk(ρ) 为该样本属于每个类别的概率

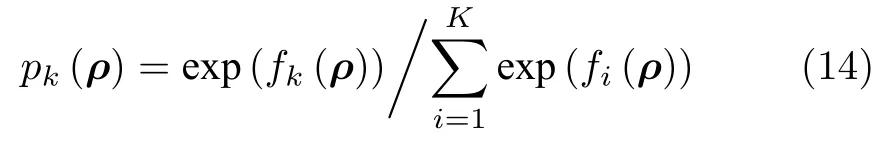
对于输入的训练T={(ρ1,X1),···,(ρN,XN)}的每个样本i=1,2,···,N,其伪残差为

利用 (ρi,rk,i)(i=1,2,···,N) 拟合一棵分类CART (Classification and regression tree)树[48],得到第m=1,2,···,M棵树共J个叶子节点权值的最佳负梯度拟合值为

则更新强分类器为

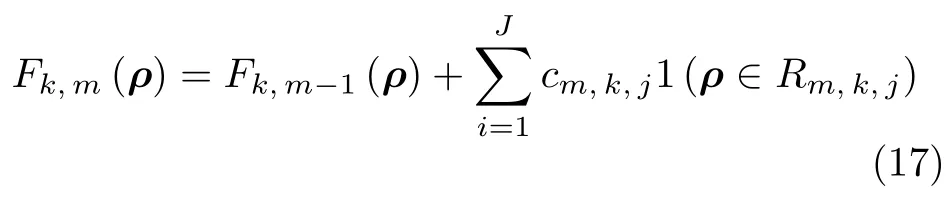
其中Fk,m(ρ)为更新得到的强分类器,1(ρ∈Rm,k,j)表示当前参数节点是否属于本次迭代残差构建的CART 树的叶节点.

当残差满足一定数值或达到迭代次数时,决策树构建完成.第2.5 节将分析设置不同参数对识别性能的影响.

2 实验与结果分析

本文所提出的多阶运动参量识别方法(Multiorder kinematic parameters based detection method,MoKiP)需要目标存在足够长的运动行程以提取运动学参数,并要求输入视频尽可能达到较高的帧率.因此,本文采集补充了以往数据集中缺失的若干常见场景数据,共同形成无人机多阶运动参量数据集 (Multi-scale UAV dataset,MUD).本文将在该数据集上分析MoKi 算法的有效性并从识别精度上与以往方法进行对比,得出本文方法的优缺点.

2.1 实验环境

本文实验所使用数据包括两部分:1)公开数据集;2)本文采集的近地UAV 数据集.本文将获得的视频以是否包含地面分为两大类,一类是近地场景,一类是对空场景.近地场景的视频中包含部分地面以及地面物体,如建筑、植物等;对空场景的视频中,背景完全为天空,不涉及地面部分.

公开数据集包括AVSS2017 无人机识别挑战数据集 (Drone-bird dataset,DBD)[23]以及运动相机飞行器探测数据集(UAV-aircraft dataset,UAD)[15].其中,DBD 包含6 段对空无人机飞行的视频,共2 130帧,背景简单,干扰目标为鸟类;UAD 包含20 段无人机和飞行器近地飞行的视频,共4 000 帧,背景相对复杂,但无干扰运动目标.

以上数据集中考虑了四旋翼无人机外观和光照的多样性.但对于无人机常见飞行场景来说,其他影响识别的重要因素,如多种干扰目标、目标尺度多样性、不同遮挡程度、不同背景复杂程度等都未得到体现,因此不能充分反映无人机在日常场景中的飞行特性.

所以,在此基础上,本文以目标尺度为依据,补充了室内场景、城市场景以及部分野外场景的无人机飞行视频.新加入的数据集不仅包含目标类别和矩形框等简单标注,而且还标记了目标的深度信息、飞行高度、相机拍摄角度以及运动参数等,形成多尺度无人机数据集 (Multi-scale UAV dataset,MUD).

干扰目标的数据来自于KITTI 车辆检测数据集[55]、RGB-D Pedestrian 行人检测数据集[56]、MoveBank[57]和NABirds 鸟类飞行探测数据集[58].表1 对比了本文采集的数据、标注情况,以及常见数据集.本文所采集数据的部分图片如图4(c)所示,所涉及的主要采集设备以及参数如表2 所示.

表2 MUD 数据集采集设备说明Table 2 Main equipment for acquisition of multi-scale UAV dataset (MUD)

图4 本文实验所用数据集示意图Fig.4 Illustration of parts of MUD used in our work

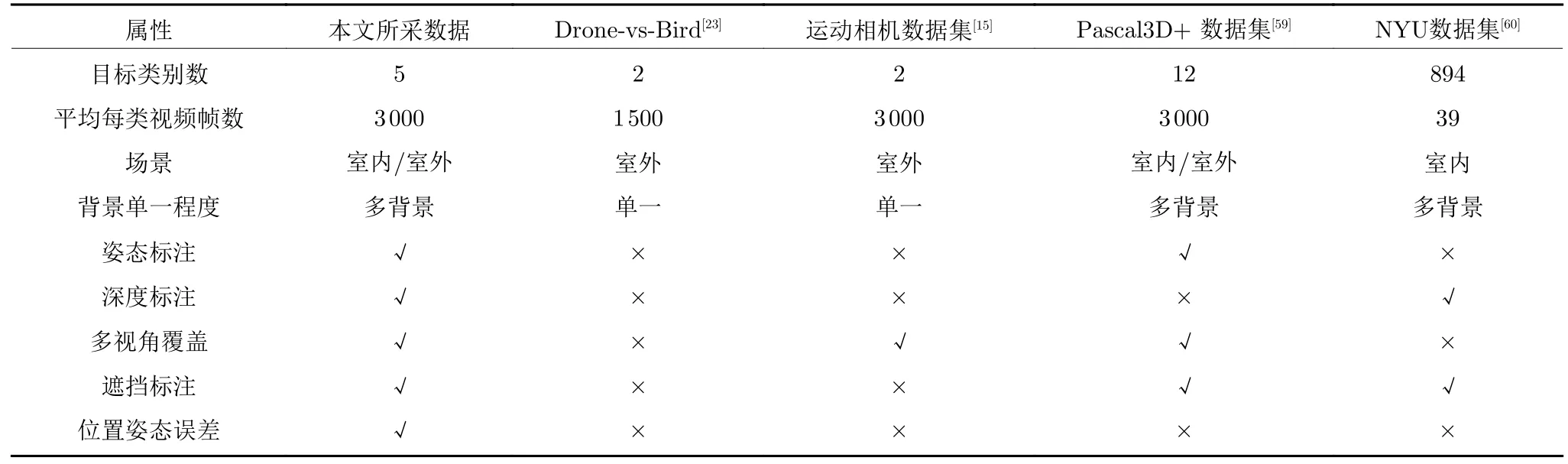
表1 本文所采集数据与其他运动目标数据集的对比Table 1 Comparison of different datasets for moving objects

本文所采集数据集相比于以往无人机和常见数据集,增加了姿态、深度、视角、遮挡以及误差的标注信息,其中误差信息为采集设备的误差.本文所涉及的目标以及干扰目标为无人机、行人、车辆、鸟类.此外,为了更好的使用这些数据,本文以是否包含地面为标准,将这些视频重新组织为两大类,一类称为近地场景,即图像中包含部分地面以及地面物体,如建筑、植物等;一类是对空场景,背景完全为天空,基本不包含可识别的地平线特征.

2.2 运动目标区域提取结果

作为本文方法流程的第1 步,根据第1.3.1 节的方法,采用运动目标提取Vibe+[30]法中设置参数前景孔洞最小尺寸为5 像素,每像素样本量为10,其余参数与文献[30]中保持一致.得到提取运动目标区域以及相机运动补偿结果如图5.

图5 为室外/室内两个场景下运动区域提取结果.其中标出的矩形窗口为获得的待识别目标的区域.由于目标为获得更高的召回率,或在召回率相近的情况下,提取出的运动区域更少.所以,为对比不同运动提取方法,所有采集视频被划分为固定长度片段,并以召回率、矩形框数量以及单位数量区域下的目标召回率(单位召回率)为指标,对比不同方法得到下表3.

表3 运动目标区域提取算法性能对比Table 3 Comparison between performance of different motion ROIs

图5 运动目标区域提取结果图Fig.5 Extraction result of motion ROIs

从3 个指标来看,Vibe+法具有更高的召回率.帧差法和光流法虽召回率也较高,但召回的假目标较多,单位召回率较低;混合高斯法召回率较低.所以对于随后的处理和识别,本文采用Vibe+法作为待识别区域提取的方法,并采用高斯混合概率假设密度滤波算法 (Gaussian mixture-probability hypothesis density,GM-PHD)方法对其进行跟踪,算法实施过程中目标检测概率、目标生存概率、平均杂波数、高斯元门限值等参数与文献[62]中保持一致.

2.3 目标深度提取

按第1.3.2 节所述,利用DORN 方法估计场景深度.对MUD 数据集中街道场景中某帧计算得到的深度图如图6 所示.其中深度真值为数据集中的标注值或通过激光测距的测量值.

图6 中,(a)为输入图像,(b)为深度估计结果,(c)为目标区域深度真值.其中白色区域为深度超过100 米的位置,可以认为无穷远背景,不予计算;对比估计结果与真值图可以看出,对于远处行人以及空中无人机,深度的估计结果与真值相符,以下将具体给出该算法以及其他算法的估计误差.

图6 深度估计结果图Fig.6 Result of depth estimation

表4 以不同估计误差参数对比了目前不同深度估计方法在本文所采用数据中的估计精度,其中误差参数定义如文献[51].其中误差项参数越小精度越高,涉及δ的误差项越大精度越高.从表中可以看出,相比于激光测距的精度,深度估计的算法误差随对探测距离的增加而明显增大.多目视觉方法在近距离的深度测量中具备较高精度以及较低的时间复杂度,但随深度的增加深度测量精度严重下降,更适合于在室内场景中使用.DORN 方法具有当前方法中最佳的精度和鲁棒性.

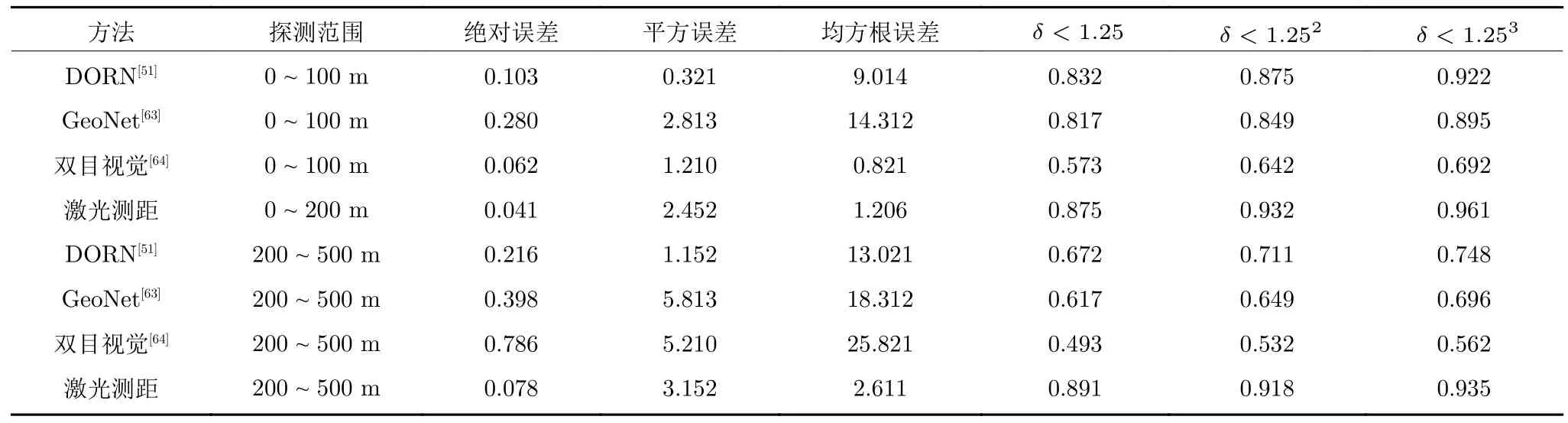
表4 不同深度估计方法误差对比Table 4 Error of different depth estimation methods

深度估计的方法亦可根据场景和需求选择其他方法.

2.4 运动参量提取

根据以上小节所得到的运动区域深度值,利用第1.3.2 节中的估计方法,可以提取出运动区域中的运动参数ρ=(v,a,ω,α),对于各个运动参量的定义和坐标设定与第2.3 节中保持一致.运动参数以及姿态真值由无人机自带的实时动态差分系统(Real-time kinematic,RTK)以及运动捕捉系统(Motion capture system,MCS)给出.其测量精度为:当GPS 正常工作时,垂直方向定位精度为±0.5 m, 水平方向定位误差为±1.5 m;若视觉定位也正常工作,则垂直方向定位精度为±0.3 m,水平方向定位误差为±0.5 m.

从图像中提取的参数,其与标定值误差如图7所示.表5 中为图7 各参数的说明.图7 中分别为目标速度、加速度、角速度、角加速度的三方向分量的估计误差以及空间定位误差,其中红色标点为典型异常值,右表为图中各符号说明.图中,采用本文方法估计得到的速度、加速度、角速度、角加速度的最小误差、最大误差以及平均误差百分数分别为:0.0,12.7,3.4 (速度参量);0.1,20.1,6.9 (加速度参量);0.0,21.2,8.3 (角速度参量);2.1,27.8,12.1 (角加速度参量).从整体来看,平动参量(速度、角速度)估计误差低于转动参量(角速度、角加速度),估计精度更高;一阶参量(速度、角速度参量)的X、Y、Z三方向分量估计精度相比于相应的二阶参量具有更高的精度.运动参量在X、Y轴方向分量的估计精度相比于Z轴相应参量分量的精度更高,估计误差的标准差也更小,所有参量中,速度参量的X、Y轴分量的估计精度最高,误差在5%以下;角加速度参量的Z轴分量误差最大,约为20%.

表5 图7 中参数对照表Table 5 Illustrations of parameters in Fig.7

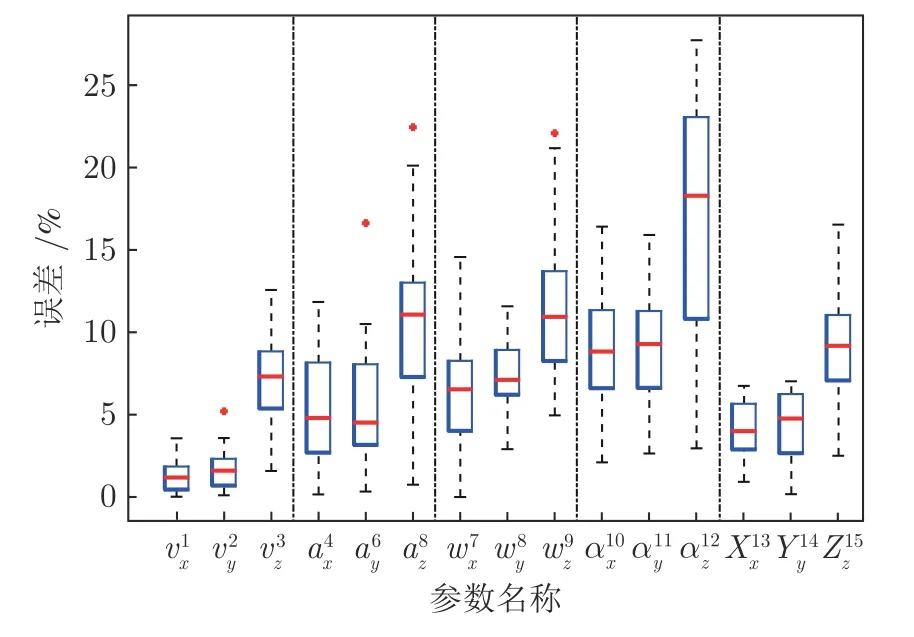
图7 运动参量估计误差箱图Fig.7 Boxplot for motion parameter error estimation

由于平动为无人机运动的主要方式,反映在图像中,目标的特征点在帧间产生明显的位移,定位的偏差相对于目标的位移相对较小,所以估计误差相对较小.而因转动产生的特征点位移较小,对特征点定位精度敏感,定位误差产生的转动参量估计的偏差会更大.

另外,二阶参量估计是在一阶参量基础上完成的,所以一阶参量的估计误差会累积到二阶参量的估计中,导致二阶参量的估计误差更高.

2.5 基于运动参量的无人机识别方法结果与分析

2.5.1 基于运动参量的梯度提升树模型的识别结果

本文采用决策树模型,利用运动学参数进行目标识别.根据文献中常用参数搭配[48]通过网格搜索法(Grid search)选择较优的参数组合,设置不同的决策树深度D、决策树数量M(弱学习器最大数量)、叶子结点数量J,获得训练集上识别精度最高的参数组合.在不同参数取值下得到无人机分类器判决接收者操作特征曲线 (Receiver operating characteristic curve,ROC) 如下.其横坐标为假阳率(False positive rate),纵坐标为真阳率 (True positive rate),用于评价模型的判决能力.ROC 曲线下面积 (Area under curve,AUC)值在 0～1 之间.越大其分类正确率越高.

如图8(a)、(b) 为设置不同的D、M、J参数时,梯度提升树训练后的ROC 曲线.图8(a)中为按训练后分类器的性能得到若干典型参数组合;图8(b)中为获得固定D、M、J参数中的两个时,另外一个单一变量对ROC 曲线的影响,用以筛选出最优参数.在图8(b)中,当固定M、J参数时,随D(决策树深度)的增大,ROC 曲线上移,说明分类器的准确率上升,但当增加到D=20后,再增大D,ROC 曲线不再上移,说明该分类器接近性能上限;当固定D、J参数时,随M(决策树数量)的增大,ROC 曲线持续上移,曲线下面积(Area under curve,AUC)从0.580 上升至0.825,但上升的幅度越来越小,M=80至M=100 相比于之前相邻曲线面积增加的0.134,下降至0.065,增长率从16.2%下降至6.7%;当固定M、D增加J(叶子节点数量)时,ROC 曲线仍上移,但当增至J=128 时,增长率相比于之前增长率下降至7.1%.总结图8(a)、(b)中各参数组合的ROC 曲线,为尽量保证训练时分类器具备较高精度,并防止过拟合现象,最终梯度提升树的参数值为D=20,M=80,J=64 (其曲线下面积AUC 值为0.812).学习率设置为0.6,子采样系数设置为0.8,损失函数为对数损失.以下是在该参数组合下,不同场景目标的识别结果.

图8 不同参数组合的ROC 曲线单参数变化时的ROC 曲线(左中右分别为 D、M、J 单独变化)Fig.8 ROC curves of different GBDT parameter combinations (The subplots from left to right are corresponding to D、M、J respectivly)

图9 为室内、对空、以及低空野外3 个不同场景下的识别结果示意.场景中除目标外,同时还包括本文所涉及的主要干扰目标,包括鸟类、行人、车辆和其他干扰目标.不同目标以不同颜色予以标识,并给出识别结果以及类别概率.从后两段识别结果来看,即使外观特征不显著的情况下,本方法也能够在运动过程中动态辨识目标,类别概率会随着目标的运动而变化.当出现典型的运动方式时,符合该运动方式的目标类别概率会明显上升,错误的类别概率就会逐渐下降,当类别概率超过50%时,则框出该目标为此类别.为消除系统累积误差,本方法将在每20 秒初始化1 次.

图9 基于运动参量决策树的无人机识别结果Fig.9 Results of MoKiP by using GBDT

训练得到的包括无人机、鸟类、行人、车辆以及其他类别的多分类器,其混淆矩阵如表6 所示.其中数字表示预测正确的样本所占该类样本总数的比例.从表中可以看出,无人机、行人、车辆的识别精度较高;鸟类的识别精度最低,混淆率较高,更容易与无人机以及其他物体飞行物体所混淆.相比于鸟类,无人机的识别精度更高,不易被其他飞行物体所干扰,但其主要干扰目标仍为鸟类.行人和车辆识别精度最高,主要由于其运动复杂度低、运动变化少,运动特性明确.总的来说,根据运动参量决策树对本文涉及的类别识别正确率(对角线数值)均能达到0.55 以上.

表6 运动参量的决策树模型识别结果混淆矩阵Table 6 Confusion matrix of MokiP by using GDBT

2.5.2 与以往方法对比分析

为对比本方法与以往不同方法的识别性能,本节以PR 曲线 (Precision-recall curve)和识别精度AP (Average precision)值为指标[11-17],给出本方法与目前几种主要 “低慢小”运动目标识别方法的性能对比,如图10 所示.

在图10 绘出了包括本文方法在内的多种目前具备较优性能的 “低慢小”识别方法在所述MUD数据集上的识别PR 曲线,所涉及方法为:基于深度光流特征的FlowNet 2.0[34]运动特征方法、Xiao等[42]采用ConvGRU(RNN)结构融合时空特征的混合方法、Schumann 等[17-18]基于Faster RCNN[12]并根据四旋翼无人机训练的改进表观特征方法、Luo等[41]引入语义信息关联相邻帧目标框的时空特征混合方法(ImageNet VID 数据集中目标的最优方法SOTA)、Rozantsev 等[15]引入相机补偿的改进Faster RCNN 方法(四旋翼无人机目标识别的最优方法SOTA)以及本文MoKiP 方法采用GBDT、GRU 神经网络的两种实现和融合方法.图中每条PR 曲线绘出随某算法召回率上升时,准确率的变化情况.每条曲线头部保持平直,准确率基本保持不变,保持在高准确率;当到达转折点时开始下降,尾部为下降过程.

图10 中曲线头部为识别方法能够达到的最高准确率.对于本文所研究的目标和数据集,以往基于运动特征的最优方法FlowNet2.0[34]的最高准确率为0.68,基于表观特征的最优方法Luo[41]的最高准确率为0.83,混合方法中的最优方法,即目前最优方法Rozantsev[15]的最高准确率为0.88.本文基于运动特征的方法(非零阶运动参量)最高准确率为0.76,混合方法最高为0.92.通过对运动特征的充分提取和细化,相比与以往基于运动和混合方法,本文方法在最高准确率(曲线头部部分)分别有0.06和0.04 的提升.但是基于非零阶运动参量的方法相对于以往表观识别方法[18,41],曲线头部准确率有0.06 左右的下降.这是由于,在低召回率的情况下,最先被召回的目标主要是像素量高、细节丰富的目标,直接利用深度网络的表观识别方法精度更高,

图10 不同识别方法的性能对比图Fig.10 Comparison of performance for different detection methods

图10 表示出本文多阶运动参量融合识别方法PR 曲线在准确率下降到95%时的转折点位置.结合表7,根据95%转折点位置可以看出,以往方法最大值位置为Recall=0.57 (方法[42]),本文基于非零阶和多阶运动参量的95%转折点分别为Recall=0.73和Recall=0.82.以往方法的PR 曲线(方法[15,18,34,41-42])都位于本文方法PR 曲线的左侧,说明本文方法随召回率升高仍能保持较高的准确率,鲁棒性强.在高召回率时主要为以往方法难以识别的困难目标,其主要表现为微像素量(目标总像素量少于150)、外观呈现形式多样、遮挡部分多,往往出现在多目标干扰的复杂背景中.但这些在表观特征中的识别困难,在本文通过运动参量形成的运动特征空间中,不同目标的运动模式差距较大,而同类目标即使外观的千差万别,却具备相似的特征运动模式.

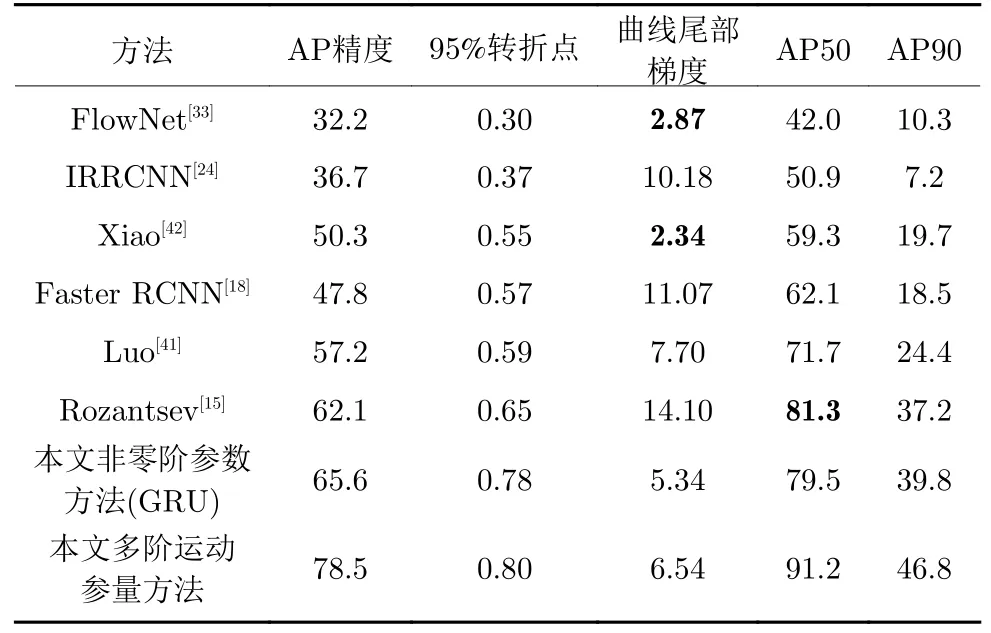
表7 不同识别方法性能指标对比表Table 7 Comparison of performance indexes for different detection method

PR 曲线95%转折点后下降部分为其尾部.本文采用尾部下降梯度参数衡量识别方法退化速度,即由95%转折点下降至准确率为0.1 位置连线的斜率,见表7.以往工作中具备较高精度的神经网络方法,包括文献[15,18,24],尾部下降梯度大于10,当在网络中加入语义以及时空约束后,方法[41]尾部梯度为7.70,相比于直接采用神经网络方法梯度下降较小.以运动特征为基础的方法[34]以及以RNN 为基础框架的方法[42],尾部梯度分别为2.87和2.34,具备最缓的下降速度,鲁棒性强.本文基于非零阶运动参量的方法和多阶运动参量方法尾部梯度分别为5.34 和6.54,为文献中最优方法[15](尾部梯度为14.10)的40%左右,下降速度更慢.这说明随着目标识别困难的增加,本文识别方法退化速度慢,鲁棒性强.

以下,本文从具体指标上,对比了不同 “低慢小”识别方法,如表7 所示.

表7 比较了本文与以往文献方法在AP 精度(AP50、AP90)、95%转折点、尾部梯度等参数上的性能差异,AP 精度数值皆为百分数.其中,文献[34]为基于运动特征的识别方法;方法[18,24,41]是以深度卷积网络为框架的基于表观特征的识别方法,文献[42]为以RNN 为框架的混合识别方法;文献[15]为融合运动与表观特征混合的最高精度方法.从表中可以看出,本文根据四旋翼无人机非零阶运动参量(运动特征)的识别方法相比于当前最优运动特征方法[34]、最优表观特征方法[41]和最优混合方法[15]分别提升33.4 (103%)、8.4 (14%)和3.5 (5%).本文融合表观特征和运动特征的多阶运动参量方法在AP 识别精度上达到78.5,相比于当前具备最高精度的混合方法[15],提升了16.4 (26%).进一步从AP50、AP90 精度来看,即当IoU 阈值分别设为50%和90%得到的识别AP 精度值,当前最优方法[15]仅在AP50 指标上具备较高精度,其余指标皆为本文方法更优.总的来说,从各项精度指标来看,本文提出的多阶运动参量识别方法(MoKiP)对于四旋翼无人机目标相比于以往方法具备更高识别精度.

2.6 一阶、二阶以及多阶运动参量的识别显著性

为进一步分析不同运动参量对识别精度的影响,本节对上文所获得决策树中的不同运动参量进行统计,并分别使用不同的参量组合对目标进行识别,最终得到不同运动参量对识别的敏感度分析.

图11 是根据第1.3.3 节所述过程以及第2.5.1节参数训练得到的一棵决策树,红色和蓝色分别是根据一阶和二阶运动参量的预测分支.

图11 训练得到的梯度提升树示意图Fig.11 A single tree from the trained GDBT

每个节点包括本分支的样本总量、各类别样本数量、基尼系数以及判别条件.

对训练得到的所有决策树,按照运动参量的阶数以及性质进行统计,通过基尼系数衡量每一类运动参数对识别的重要程度,则参量贡献度D被定义为:

Giniρ为在所有训练得到的决策树中采用某类参量ρ为切分变量的节点的基尼系数.按参量不同性质,得到参量贡献度占比表,见表8、表9 所示.

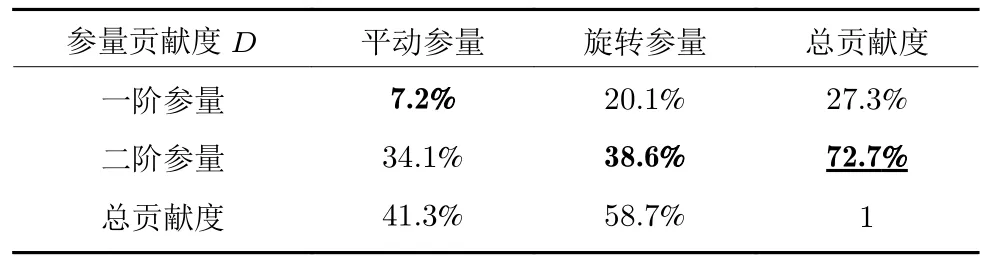
表8 运动参量的性质对无人机识别的影响表Table 8 Impact of the parameter properties on UAV detection

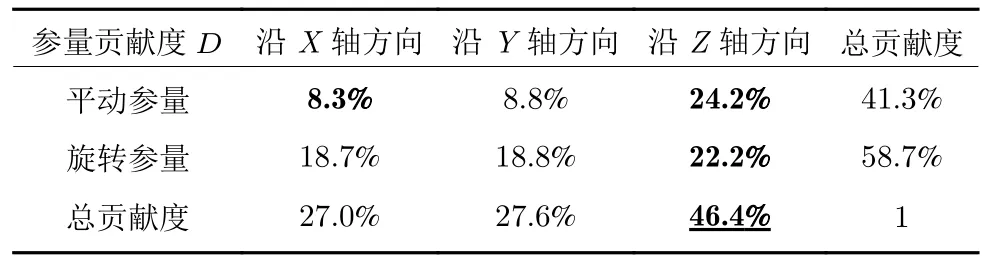
表9 运动参量的方向对无人机识别的影响表Table 9 Impact of the parameter direction on UAV detection

表8 中所涉及的一阶参量包括速度、角速度,二阶参量包括加速度、角加速度;平动参量包括速度和加速度,旋转参量包括角速度和角加速度.其中一阶平动参量和旋转参量分别占7.2%和20.1%的贡献度;二阶平动参参量和旋转参量分别占34.1%和38.6%的贡献度.在表中所涉及的参量中,一阶平动参量贡献度最低,二阶旋转参量贡献度最高,相同阶数的旋转参量比平动参量贡献度更高.从总和来说,二阶运动参量对本文提出模型的贡献度最大,达到72.7%;一阶参数贡献度为27.3%,仅为二阶参量的38%,说明在识别过程中二阶运动参量起了更重要的作用.从运动方式来说,旋转参量相对于平移参量,能更大程度上反映出目标的特征.综上,二阶参量是无人机识别过程中的重要参量,精确估计二阶旋转参量是本文识别方法的基础.

表9 显示了运动参量的方向性对识别的影响,其中所述沿X、Y、Z轴方向参量与第1.3.2 节保持一致.表中沿X轴方向平动参量贡献度最小为8.3%,沿Z轴(即重力方向)方向的平移参量贡献度最大为24.2%.沿X轴和Y轴的运动参量在各贡献度数据上都相近,并均低于相应Z轴方向运动参量,其中平移参量在数值上低15.4%,旋转参量低3.4%.从总贡献度来看,Z轴方向参量总贡献度比Y轴总贡献度高68.1%.这说明Z轴方向运动参量为识别过程中的主要参量,沿Z轴方向的运动是无人机区别于其他目标的主要运动方式.

进一步,本节通过剥离实验,采用不同的运动参量组合对四旋翼无人机进行识别,获得以下识别结果.

图12 中,图12(a)、(b)为采用本文所涉及的一、二阶运动参量组合进行识别的结果;图12(c)、(d)为采用二阶以上高阶运动参量识别结果.图中X、Y、Z轴方向与第1.3.2 节中保持一致.图12(a)为单独采用单一运动参量(分量)进行识别的结果,其中蓝绿黄色分别代表沿运动参量X、Y、Z轴分量结果.其中单独使用速度参量Y轴分量识别的精度最低,为0.07;单独使用加速度Z轴分量识别的精度最高,为0.22.单独使用二阶参量均高于单独使用一阶参量的识别精度;单独使用Z轴方向分量的识别精度高于相应参量在X、Y轴分量的精度.这也从另一侧面印证了表7、8 的结论,即二阶运动参量以及运动参量的Z轴分量是无人机识别过程中的重要参量.

图12 不同参量组合的识别结果图Fig.12 Detection results of different parameter combinations

图12(b)为采用本文所涉及的运动参量不同组合进行识别的精度对比.其中,基础运动参量为一阶、二阶、平动、旋转等参量组合,再将不同的其他参量加入到基础运动参量中后,得到不同参量组合的识别结果.两参量组合的基础运动参量结果体现出与表7 一致的结论,使用二阶参量(0.48)相比于一阶参量(0.31)识别精度更高,在识别中的贡献度更大,为更重要的运动参量;旋转参量(0.47)稍高于平动参量(0.41)的识别精度.在三参量组合中,组合识别精度最高为0.60,高单精度最低为0.51.在基本参量中,相比于加入速度和角速度参量的最大提升0.10 (24.3%),加入加速度、角加速度参量的提升更大,最小提升为0.13 (27.6%).进一步说明二阶参量在识别过程中为更重要的参量、更显著地影响识别效果.

图12(c)、(d)绘出了使用不同阶运动参量识别的结果.图12(c)为单独使用某一阶运动参量识别的精度结果;图12(d)为使用前若干阶运动参量识别的精度结果.由于在运动学中描述物体运动均采用一阶和二阶运动参量,所以本文也主要使用二阶及以下运动参量进行识别.但从参数辨识和运动特征提取的角度来说,由于采集得到的均是离散的数据,想要尽可能精确地估计得到运动参量或者恢复目标整个运动过程,只能基于近似的方法.根据泰勒展开,任意运动轨迹上的一点的位置均可由其在选定点多阶导数形成的多项式进行逼近,而所涉及的多阶导数,即为本文所涉及的一阶、二阶以及高阶运动参量.同样,对于整个转动过程也需要利用多阶旋转参量进行逼近.另一方面,越高阶的运动参量越能够反映目标在更长一段时间内运动的整体特征.所以,在识别过程中使用高阶运动参量是有必要的.

从图12(c)中看出,单独使用一阶运动参量精度为0.311,单独使用二阶运动参量精度为0.480,单独使用三阶参量精度下降至0.059,四阶参量精度下降69.5% 至0.018,到六阶的识别精度仅为0.003,说明三阶以上运动参量识别贡献度显著降低.再结合图12(d)前若干阶参量总识别精度来看,使用一、二阶参量识别精度为0.656,三阶参量引入后识别精度上升至0.681,增幅3.8%;四阶参量引入后,增幅仅为1.3%;至六阶参量引入,总识别精度为0.697,增长为0.2%.总的来说,三阶以上总识别精度未有显著增长,一、二阶运动参量能较完整的包含目标的全部运动特征.

3 结论

本文提出了一种基于运动参量建模的 “低慢小”目标识别方法.相比于以往方法,本方法进一步完善了运动特征的描述,并在所涉及的数据集上,相比于以往文献中的方法,显著地提升了四旋翼无人机的识别精度.在实验中本文也发现,二阶参量、旋转参量、以及重力方向的运动参量是四旋翼无人机识别过程中的重要参量,反映出目标在运动模式上的差异.