污水处理过程出水水质稀疏鲁棒建模
闻超垚 周 平
随着工业化的发展和生态污染的加剧,我国水资源短缺问题日益严重,已经成为制约经济社会发展的瓶颈问题.污水处理可有效缓解水资源匮乏问题并且减少环境污染[1-2].活性污泥法是目前最为常用的污水处理方法[3],其利用微生物菌群的生物特性,通过硝化、反硝化等生物化学反应,对污水中的可溶性有机物进行分解和氧化,从而使得污水得到净化,达到排放标准.活性污泥法污水处理过程工艺示意图如图1 所示,污水首先经过格栅间去除较大体积的固体污染物,然后通过进水泵的作用进入初沉池,去除大部分固体悬浮物.经过初沉池的出水进入生化反应池,生化反应池是活性污泥法的核心环节,分为厌氧区和好氧区两个部分.在厌氧区,利用厌氧菌的无氧呼吸完成反硝化反应,可以将污水中的硝态氮还原成氮气释放出来;在好氧区,通过硝化反应将氨氮转化成硝酸盐,回流到厌氧区进行反硝化反应使有机物被降解.最后,经过生化池处理的出水流入二沉池进行固液分离,上层清水从出水口排出进行消毒处理,以使水质达到排放标准.而下层沉淀后的污泥一部分继续回流到生化池中,另一部分污泥与初沉池的污泥混合经过浓缩、消化、脱水等处理后回收利用.

图1 污水处理过程工艺流程图Fig.1 Wastewater treatment process flow diagram
污水处理是一个具有复杂生化反应的非线性、大滞后、强耦合典型流程工业系统,包含诸多重要的生产数据,现场操作人员会利用工业数据对某些特别关注的关键指标进行监测,从而调控整个生产过程,最终实现稳定生产的目标[4-6].目前,在污水处理过程中被广泛关注的指标为出水的水质指标,主要包括生化需氧量(Biochemical oxygen demand,BOD)、化学需氧量(Chemistry oxygen demand,COD)和总悬浮物(Total suspended solid,TSS).污水水质指标不仅是用来衡量污水处理过程正常与否的重要标志,还可以反映过程内部的具体状态变化.因此,对水质指标进行实时准确地测量可以为污水处理厂的工作人员提供操作参考.然而,污水处理过程受进水流量、微生物种群、溶解氧浓度、PH 值等的影响,使得整体过程反应机理极其复杂,内部环境恶劣,难以进行水质指标的实时在线直接检测,通常需要进行离线检验.然而离线检验的时滞会严重影响污水处理操作的实效,并且容易造成二次污染[6].所以建立准确的水质指标估计模型来反映当前水质情况和预期的水质指标变化,进而为污水处理过程的操作与优化提供重要指导.
目前常见的水质指标建模方法包括机理建模和数据驱动建模两种.机理建模需要对整体工艺机理有着深入了解,并在满足一定假设条件的基础上,依据大量的专家知识才能够建立.正是因为这些假设条件和人为经验的限制,使得机理模型的实际应用精度极低,实用性差.与机理建模方法不同,数据驱动建模不需要先验知识和各种假设条件,只需借助于机器学习、统计学习等智能算法主动学习输入输出样本数据之间的映射关系,就能够获得比较好的建模精度.随着工业过程各种数据可用性的提高以及数据处理能力的增强,数据驱动水质指标智能建模方法越来越受到研究者的重视,相关文献先后提出了偏最小二乘(Partial least squares,PLS)建模方法[7-8]、支持向量机回归(Support vector regression,SVR)建模方法[9-10]和人工神经网络(Artificial neural networks,ANNs)等水质指标建模方法[2,6,11-12].尤其以ANNs 为代表的数据驱动建模技术已经成为了水质建模的主要方法.文献[2]使用前馈神经网络建立出水氨氮和总氮浓度的预测模型,实验表明该方法具有较好的模型精度.文献[6]提出了一种基于类脑模块化神经网络的关键出水参数软测量方法,通过模拟大脑皮层模块化分区结构,构建软测量子模型对各水质指标进行同步测量.虽然利用ANNs 建立水质指标模型取得了很大的进展,但是常规ANNs 建模算法普遍存在过拟合、易陷入局部极小的问题,并且基于批学习的网络权值和偏差迭代算法容易造成模型训练时间长、收敛速度慢的系列问题[13].
近十年来,随机权神经网络[14](Random vector functional-link networks,RVFLNs)利用简单易实现的网络结构,改善了现有ANNs 建模普遍存在的收敛速度慢、泛化能力不强、实用性差的问题,大大提高了模型的计算精度和计算效率.RVFLNs的建模原理是在给定训练范围内随机选取输入权值和隐含层偏置,通过最小二乘(Least squares,LS)估计求得隐含层和输出层之间的权值.与传统ANNs 相比,RVFLNs 可以获得更快的训练速度和可接受的精度.此外,RVFLNs 的万能逼近能力在理论上也得到了证明[15-18].因此,基于RVFLNs 的数据驱动质量建模已经被广泛应用到污水处理过程中.文献[19]采用基于智能算法优化网络参数的RVFLNs 实现了BOD 的在线软测量.文献[20]提出了一种选择性集成RVFLNs 水质指标建模方法,并应用到某工业污水处理厂的水质测量,有效解决了传统ANNs 水质模型测量精度低、性能不稳定的问题.但是,实际污水处理过程中,受检测仪表等装置的故障等不可避免的影响,测量数据中经常存在各种各样的离群点,即由于人为或设备故障而产生的远离其他大部分样本的极大值或极小值[13,21].同时,RVFLNs 在实际应用中,隐含层矩阵会因为隐含层参数的选取不当造成多重共线性问题,即隐含层矩阵的列向量之间存在相关关系,使得LS 估计失效[22].为此,有学者提出用PLS 代替LS 估计求解输出权值,并将这种网络结构称为偏最小二乘随机权神经网络(PLS-RVFLNs)[22].虽然PLS-RVFLNs可以不受多重共线性的影响,但是PLS 在计算时用到了隐含层矩阵的所有列,并且没有考虑离群点的影响,导致利用PLS-RVFLNs 进行建模的水质模型精度不高且计算效率较低.综上,由于实际污水处理过程的复杂动态特性和RVFLNs的结构特点,多重共线性和离群点问题必然存在,基本的RVFLNs和PLS-RVFLNs 模型不能为现场操作人员提供准确可靠的指导.
针对上述问题,本文提出一种基于稀疏偏最小二乘(Sparse partial least squares,SPLS) 和Schweppe 型广义M 估计(Generalized M-estimation,GM-estimation)的RVFLNs 稀疏鲁棒建模方法(GM-SPLS-RVFLNs),并用于污水处理过程的出水水质指标的在线鲁棒估计.与现有鲁棒估计方法相比,本文方法具有良好的稀疏性,可以自主地选择与输出变量相关的隐含层变量,有效地提高模型的计算效率.同时,所提模型不仅考虑输入输出样本均含有离群点的情况,而且还考虑了输入输出样本离群点之间的相互影响,可以增强模型在遇到离群数据时的泛化能力.最后,进行建模仿真实验,并和其他几种建模算法进行对比.结果表明,当输入输出数据均含有离群点时,本文方法不仅具有更高的模型精度,而且可以解决常规RVFLNs 水质指标模型存在的多重共线性问题.
1 稀疏鲁棒建模策略
为保证污水处理厂持续、稳定、高效运行,对污水处理的出水水质指标进行实时检测及评估至关重要[6].常用的水质指标有化学性指标BOD、COD 和物理性指标TSS 等.BOD 是指水中能够分解的有机物完全氧化分解所需要的溶解氧量.COD是指在一定的条件下,水中的有机物在强氧化剂的作用下发生氧化还原所需要的氧气量.BOD 和COD这两个水质指标都需要进行水质化验才可以获取,通常化验的过程会花费较长的时间,导致后续操作得不到保障.物理性指标TSS 是指水中不可过滤的悬浮物,是用来检验在污水处理过程中过滤效果好坏的指标,由于污水处理过程的环境特性,TSS 的含量不易直接测量[23].
为了实现对关键水质指标BOD、COD 和TSS进行在线估计或预测,基于随机权神经网络(RVFLNs)的智能建模与稳健估计等技术,建立多元水质指标非线性自回归(Nonlinear autoregressive exogenous,NARX)模型.基本RVFLNs 建模时,输入层通过激活函数的作用映射到隐含层特征空间,而其训练过程可以看成隐含层与输出层之间的线性回归问题,回归系数就是输出权值.基本RVFLNs 在求解输出权值时,采用的是最小二乘(LS)估计.众所周知,当数据满足高斯-马尔柯夫定理的假设条件时,LS 估计是最佳的线性无偏估计.然而,污水处理等众多实际工业过程的运行数据往往不满足高斯-马尔科夫定理的基本假设,使得LS 估计出现多重共线性和鲁棒性差的问题.为此,本文提出一种稀疏鲁棒建模方法,建模思路及要点如下:
1)多重共线性的存在经常会导致利用LS 估计求解的回归系数产生病态解,致使模型的输出权值不稳定,不利于水质指标模型的建立.为了解决多重共线性的影响,本文提出采用稀疏偏最小二乘(SPLS)求解模型的输出权值.SPLS 是偏最小二乘(PLS)的稀疏版本,继承了PLS 可以解决多重共线性问题和可以实现高维数据降维的优点,同时在求解过程中可以进行变量选择与约简,直接将影响较小的变量所对应的回归系数压缩为0,进而增强了模型的可解释性和计算精度.
2)为了提高模型在遇到同时含输入输出离群点数据时的泛化能力,本文进一步采用Schweppe型广义M 估计对模型的鲁棒性能进行改进.Schweppe 型广义M 估计是稳健估计理论中较为常用的统计方法,这种方法不仅考虑离群点与大多数样本点之间的关系,而且还充分考虑模型输入输出样本离群点之间的关系,可以对离群点进行合理处理,降低离群点在建模过程的建模权重,有效减小离群点对建模过程的干扰,进而提高水质指标模型的泛化能力.
2 稀疏鲁棒建模算法
2.1 基本RVFLNs
Pao 和Takefuji 于1992 年首次提出随机权神经网络(RVFLNs)[14-18],其最大特点是输入层权值和隐含层偏置在特定范围内随机选取,输出权值由Moore-Penrose 广义逆矩阵和最小二乘(LS)估计计算得出.因此,RVFLNs 与基于梯度的学习算法不同,不需要事先设定过多参数,也不需要花费大量的时间才能使算法收敛.RVFLNs 凭借训练速度快、泛化能力强、较少的人为干预、便于实现在线学习的优点使其在实际系统回归、分类等建模问题中得到广泛应用[13,19-22].
给定N组任意不同观测样本训练数据集Z={(xi,yi)|xi ∈Rn,yi ∈Rm,i=1,2,···,N}, 其中xi,yi分别为n维输入向量和m维输出向量,则具有L个隐含层节点,且激活函数为g(x) 的RVFLNs 可以表示为:

式中,fL,i(xi) 是第i个样本的模型输出值,βj=[βj1,βj2,···,βjm]T是第j个隐含层节点与输出层之间的输出权值向量,wj,bj分别是第j个隐含层节点在给定范围内随机生成的输入权值向量和隐含层偏置向量的第j个元素,wj·xi表示wj与xi的内积.
RVFLNs 学习目标是使模型输出fL,i(xi) 和实际样本输出yi之间的误差最小,即该问题等价于存在βj,wj和bj,满足以下条件:
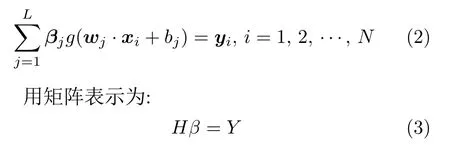
式中,H为隐含层输出矩阵,β为输出权值矩阵,Y为观测样本的真实输出矩阵,分别表示如下:

一般来说,训练集的样本数会远大于隐含层节点数,此时H不是方阵,那么输出权值β就需要使用LS 估计对输出权值矩阵进行求解:

式中,H†为隐含层输出矩阵H的摩尔-彭若斯广义逆矩阵,此时唯一且其范数最小.
2.2 稳健估计
实际工业数据中会包含大量的离群点,这些离群点既包含输入样本的离群点,又包含输出样本的离群点,直接导致水质指标估计模型的失效.当样本数据含有离群点时,可通过选择合适的稳健估计方法来避免离群点的影响,得出正常数据情况下的最佳估计值.因此,借助稳健估计方法来提高模型的鲁棒性,最常用稳健估计方法为M 估计[24].对于给定数据集则线性回归方程表示如下:

式中,β为回归系数向量,r为残差向量.
利用LS 估计求解回归系数β的优化目标函数为:
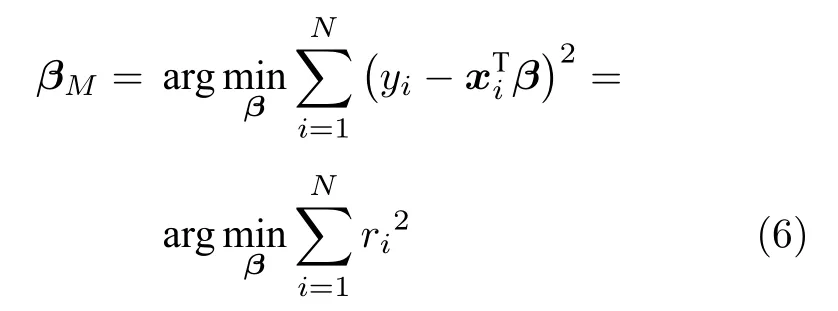
若r符合高斯分布,则LS 估计的回归系数βLS为最优估计量.然而,实际残差向量r会受离群点的干扰而非高斯.在这样的情况下,LS 估计就会失去最优性.M 估计对LS 估计的目标函数进行了改进,使其更适合数据中包含离群点的情况,改进之后的优化目标函数定义如下:
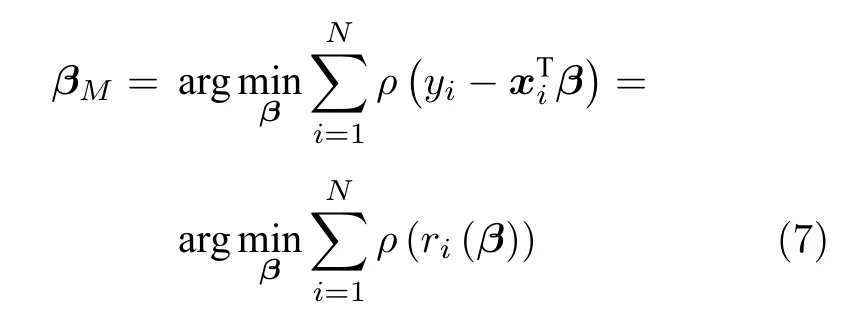
式中,ρ是M 估计的影响函数,而且通常有界非递减.

式中,wi可以看成是残差项ri的建模权重.如果ri过大,说明其所对应的样本点yi是离群点,相应地建模权重wi可以比较小,进而减小该离群点对建模过程的影响.通过推导,不难看出M 估计仅仅对输出样本的离群点进行了权值处理,但没有考虑输入样本含有离群点的情况.因此,为了改善M 估计对输入样本的异常数据相对敏感的问题,广义M 估计算法相应而出[24].广义M 估计考虑了输入输出样本都存在离群点的情况,通过减小输入输出样本中的异常点在建模时的权重,降低离群点对建模过程的不良影响.
为了能够计算输入样本的建模权重,需要将M估计方程(9)改写成如下形式:
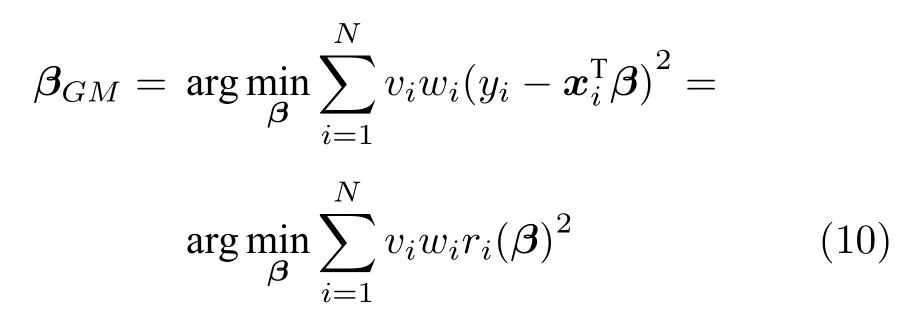
式中,vi为输入样本点xi的建模权重.若xi偏离大部分数据,则vi较小,这样就达到了减小输入样本离群点建模权重的目的.
2.3 GM-SPLS-RVFLNs 稀疏鲁棒建模算法
2.3.1 SPLS-RVFLNs
RVFLNs 的输入权值和隐含层偏置在一定范围内任意选取之后,其训练过程就可以转化为隐含层矩阵H与输出样本矩阵Y之间的线性回归模型.然而,隐含层矩阵H会存在多重共线性,使得LS估计求解的输出权值不稳定.为了解决多重共线性问题,文献[25]在偏最小二乘(PLS)的基础上,提出了一种稀疏偏最小二乘回归(SPLS)的计算方法,通过对标准化的输入输出数据进行潜变量的提取,利用提取的潜变量进行回归求解.SPLS 在PLS 的求解过程中加入Lasso 罚约束进行变量选择,使得模型的回归系数具有稀疏性,只保留对输出变量有主要影响变量的回归系数,能够提高模型的预测精度.本文利用SPLS 代替LS 估计求解,得到稀疏偏最小二乘随机权神经网络(SPLS-RVFLNs).SPLSRVFLNs 不仅可以解决隐含层矩阵H的多重共线性问题,还可以增强模型的可解释性和计算精度.
对于N个样本数据集Rm,i=1,2,···,N},具有L个隐含层节点,激活函数为g(x)的RVFLNs 隐含层矩阵H∈RN×L和输出矩阵Y∈RN×m分解如下:
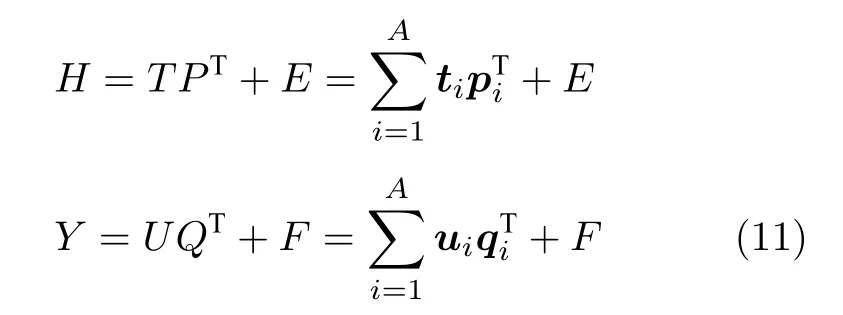
式中,T=[t1,t2,···,tA]∈RN×A,U=[u1,u2,···,uA]∈RN×A分别是隐含层矩阵和输出矩阵的全部潜变量矩阵,A是潜变量个数;P=[p1,p2,···,pA]∈RL×A,Q=[q1,q2,···,qA]∈Rm×A分别是隐含层矩阵和输出矩阵的负载矩阵;E ∈RN×L,F ∈RN×m分别是隐含层矩阵和输出矩阵的残差矩阵.隐含层矩阵和输出矩阵的潜变量ti和ui的提取原则是在满足单位正交约束和Lasso 罚约束条件下,按照ti和ui的相关性最大的原则依次提取,即:

式中,λ1,λ2分别是隐含层矩阵和输出矩阵权重向量wi和ci的Lasso 罚参数,决定了wi和ci的稀疏程度.λ1,λ2的选取与权重向量的具体数值有关,在确定某个数值之后,可以使得权重向量中小于这一数值的分量为0.因此,为了使得权重向量wi和ci的稀疏性达到最大,可以使λ1,λ2分别为权重向量wi和ci每个分量的最大值.此外,权重向量wi和ci的计算公式分别为,wi=式中gλ1(x)=sign(x)(|x|-λ1) 和gλ2(x)=sign(x)(|x|-λ2)是软阈值函数.
最后,推出最终隐含层矩阵和输出矩阵之间的SPLS 回归模型如下:

式中,βSPLS为SPLS-RVFLNs 的输出权值,F为残差,W=[w1,w2,···,wA]∈RL×A是隐含层矩阵的权重矩阵,B=[b1,b2,···,bA]∈RA×A是隐含层矩阵潜变量和输出矩阵潜变量之间的回归系数矩阵,其中
注 1.SPLS 能够从输入变量集与输出变量集中分别提取出方差变化最大的潜变量,同时在满足一定正交性和归一化约束的条件下保证输入输出变量集潜变量之间协方差最大,之后利用提取出来的潜变量进行回归求解,具体的SPLS 求解公式如式(12)所示.由于提取的潜变量不存在多重共线性问题,并可最大程度地保留原输入输出数据所蕴含的信息,因此可以有效解决多重共线性问题对数据建模的不利影响.
2.3.2 GM-SPLS-RVFLNs
SPLS-RVFLNs 的输出权值由SPLS 进行求解,当输入输出数据中存在离群点时,SPLS 的计算效果会受到影响,使SPLS-RVFLNs 模型的建模精度变差.作为稳健估计技术的一种,广义M 估计可以有效提高模型的建模精度,其通过对输入输出数据包含的离群点进行降权处理,使模型的估计值接近正常模式下的最佳估计值.但是,如果不考虑与输入样本异常值相应的输出样本对大部分数据的拟合情况,任何对输入样本数据的降权处理都不会有效[26].为此,Schweppe 型广义M 估计考虑了输入输出样本异常值与大部分数据之间的拟合关系,只有当残差较大并且输入样本是离群点的时候,才会进行降权处理,因此可更准确地识别并处理离群点.综上,为了减小离群点对SPLS-RVFLNs 模型造成的不良影响,利用Schweppe 型广义M 估计(GMestimation)对SPLS-RVFLNs 进行鲁棒性改进,提出一种新型的RVFLNs 稀疏鲁棒建模算法(GMSPLS-RVFLNs).
首先,利用SPLS 对SPLS-RVFLNs 的输出权值βSPLS进行求解,如下所示:
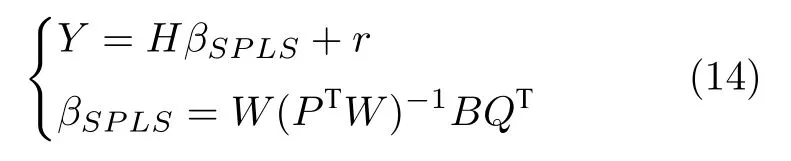
式中,r为残差.
其次,为了能够降低离群点对SPLS-RVFLNs的影响,利用下式计算输入样本的建模权重:

式中,f为稳健估计的权函数,‖·‖是欧几里德范数,c为调谐参数,medL1(T) 是利用隐含层矩阵的潜变量{t1,···,tn}计算的L1中值.L1中值是一种具有良好统计特性的多元位置稳健估计量,它的基本原理是对于数据集X={x1,···,xn},xi ∈Rp,寻找满足以下条件的μ,即:
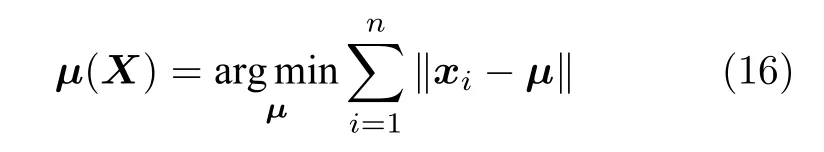
简单来讲,L1中值是此点到n个给定样本点欧氏距离之和最小的点.L1中值最大可以容忍50%样本数量的离群点,并且满足尺度同变性和位置不变性[27].
为了同时考虑每个样本点在输入输出方向都异常的情况,采用Schweppe 型广义M 估计,其输出样本建模权重不仅用到了残差,还用到了输入样本的建模权重,计算公式如下:
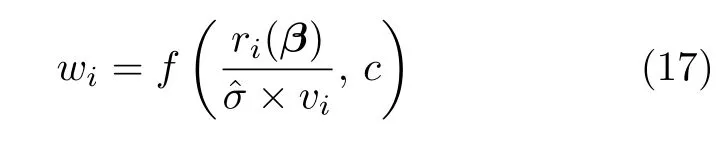

式中,median(·)是中位数函数.
稳健估计的权函数有多种选择,如Hampel 权函数、Tukey 双权法权函数、Andrew 正弦法权函数等[24].一个好的权函数不但会影响模型的鲁棒性能,而且还会影响模型的计算效率.一般来说,理想的权函数通常需要满足这样的性质:当样本数据在分布中心时,每个样本被给予相同的权重;当样本数据越靠近分布两端时,其权重越小.
本文首先利用Fair 权函数计算输入样本的建模权重.Fair 权函数通过选取适当的调谐参数c来满足模型的鲁棒性能和计算效率.一般来说,Fair权函数的调谐参数c=4,计算公式为:

建模权重利用标准化残差进行计算,如果标准化残差较小,说明此时的样本点不是离群点.Fair权函数计算得到的权重则接近1,保留了其在建模过程中的权重.如果标准化残差较大则说明此时的输出样本点是离群点,通过Fair 权函数的作用会使得其权重接近零,达到了降低离群点建模权重的目的.
然后,利用Huber 权函数计算输出样本的建模权重.Huber 权函数设置了参数范围,超过这一范围的样本点被给予较小的权重,超过越多,其权重越小;在这个范围之内的样本点,代表是正常数据,直接让建模权重为1.Huber 权函数的表达式如下:

式中,c为Huber 权函数的调谐参数,一般取值为c=1.345,这样不仅可以保证模型能够较好地减小离群点的影响,而且还能够获得类似正常情况下LS 估计结果.
最后,输入输出建模权重都确定之后,可以对隐含层矩阵H和输出样本矩阵Y进行加权处理:

利用加权后的隐含层矩阵和输出样本矩阵进行SPLS 计算,得到最终的输出权值.
2.4 算法实现步骤
所提GM-SPLS-RVFLNs 算法的主要建模过程及实现步骤总结如下:
1)给定数据集Z={(xi,yi)|xi ∈Rn,yi ∈Rn,i=1,2,···,N}, 初始化网络的隐含层节点个数L和激活函数g(x),在一定范围内随机选取输入权值wj和偏置bj,并计算隐含层矩阵H;
3)根据式(15)和式(19)计算隐含层矩阵潜变量T的权重vi;
4)根据式(18)计算残差r的稳健尺度估计,代入式(17)和式(20)计算输出样本Y的权重wi;
5)根据式(21)计算加权后的隐层矩阵和输出矩阵并进行SPLS 回归计算,得到输出权值并返回步骤3)重复迭代计算得到直到每个参数估计值1,···,L,h=1,···,m都小于设定的迭代停止条件,则停止迭代,并且令最后一次计算的输出权值为模型的最终输出权值.
3 数据实验
3.1 模型建立
本文利用BSM1 (Benchmark simulation model NO.1)[3]污水处理基准仿真平台进行数据仿真实验.BSM1 基准仿真平台是由国际水质协会和欧盟科学技术合作组织合作开发,能够方便调整各种控制策略以得到较优的实施方案.并且对于不同的控制方法,还能利用相同的性能评价指标进行比较分析.BSM1 模型的结构和污水处理工艺流程相近,由生化池和二沉池两大部分组成.此外,本文鲁棒建模为了能够更加充分地模拟不同比例离群点存在的真实工业数据情况,在BSM1 数据中人为加入了不同比例输入输出样本离群点.通过分析污水处理的工艺流程可以得到出水质量与固体悬浮物的数量以及各种有机物的含量直接相关.因此,利用BOD、COD 和TSS 这3 个常用的水质指标作为建模输出变量Y.在充分考虑污水处理过程工艺机理和基准仿真平台特性的基础上,确定影响出水水质指标的6 个关键变量作为建模输入变量X.同时,考虑到污水处理过程具有大时滞性,为了更好地反映输入输出变量之间的时序关系,我们将当前时刻的输入变量X(t)、上一时刻的输入变量X(t-1) 和上一时刻的模型输出变量Y(t-1) 一起作为模型的输入量,建立污水处理出水水质指标的多元非线性自回归(NAXR)模型.
确定模型的输入量和输出量之后,接下来需要确定模型的参数.基本RVFLNs 需要确定的参数有输入权值wj、隐含层偏置bj和隐含层节点数L,其中wj和bj一定范围内随机选取,所以只需要确定wj和bj的选取范围.Schmidt 等通过实验确定了wj和bj的选取区间[-1,1][29],此区间已经成为了RVFLNs 的理论研究和实际应用的指导方针.因此,所提GM-SPLS-RVFLNs 算法也在[-1,1]区间内随机选取输入权值wj和隐含层偏置bj.此外,隐含层节点数L和潜变量个数A也是重要的模型参数,本文利用实验方法确定隐含层节点数L和潜变量数A.首先,将隐含层节点数L从10 到200 依次5 个增加,潜变量个数A从1 到20 依次逐个增加,代入到模型中进行计算.其次,由于wj和bj具有随机性,会造成每次实验结果不唯一,因此利用每次选取的隐含层节点个数L和潜变量个数A进行30次重复计算,并计算30 次试验建模误差的均方根误差(Root mean squared error,RMSE)均值,最后得到实验结果如图2 和表1 所示.图2 为隐含层节点数L和潜变量数A与模型误差的关系图,可以看出当潜变量个数A为10 时,模型误差开始逐渐减小.表1 为潜变量数A为10 时,不同隐含层节点数的RMSE 值,可以看出当隐含层节点数L为35 时,模型的误差变化趋于平缓.因此,选取神经网络隐含层节点数L为35,潜变量A的个数为10.

表1 10 个潜变量时,建模误差与隐含层节点个数之间的关系表Table 1 The relationship between the RMSE and the number of hidden layer nodes when 10 latent variables

图2 建模误差与潜变量和隐含层节点数的关系图Fig.2 The relationship between the RMSE and the number of latent variables and hidden layer nodes
3.2 数据实验结果与分析
为了能够全面地验证所提算法的鲁棒性能,在BSM1 建模数据基础上增加两类不同的离群数据集.第一类数据集用来测试所提算法对只有输出样本离群点时的建模效果;第二类数据集用来测试所提算法对输入输出样本均含离群点时的数据建模适用性.
首先,第一类数据集是在限定离群点最大幅值的情况下,比较所提算法对输出样本包含不同比例离群点时的预测精度.从建模数据中随机挑选间隔为5%、比例依次为0%,5%,10%,···,50%的样本点yi,Outlier,并对挑选的样本点进行如下离群处理:
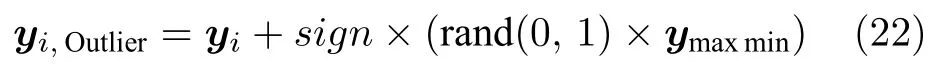
式中,ymaxmin是正常状态下各个水质指标最大值与最小值之差.为了使得样本数据中的离群点更加不均衡,对挑选的样本点设定比例为2:1 的正向离群点和负向离群点,当离群点为正向时令sign=1,当离群点为负向时令sign=-1.
其次,第二类数据集是在限定离群点最大幅值的情况下,比较所提算法针对输入输出样本均包含不同比例离群点时的预测精度.输出样本的离群点设计方法与第一组数据集的设计方法一致,输入样本从建模数据中随机挑选间隔为10%、比例依次为5%,15%,25%,35%的样本点xi,Outlier,并对挑选的样本点进行如下离群处理:
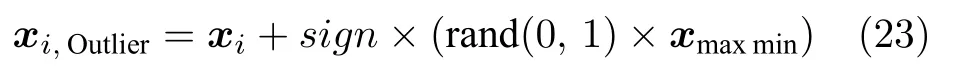
式中,xmaxmin是输入变量的最大值与最小值之差,并且对挑选的样本点设定比例为2:1 的正向离群点和负向离群点.
为了验证所提GM-SPLS-RVFLNs 方法对水质指标的建模效果,将其与基本RVFLNs、基于M估计的鲁棒随机权神经网络(Robust RVFLNs)[13]和采用鲁棒偏最小二乘回归(Partial robust M-regression,PRM)[30]进行输出权值求解的随机权神经网络(PRM RVFLNs)进行比较,如图3~7 所示.四种方法都使用相同网络参数设置:激活函数均为Sigmoid 函数,隐层节点数L为35 个,输入权值wj和偏置bj的取值范围均为[-1,1].此外,为了避免每次计算选取输入权值wj和偏置bj的随机性,对每一组数据集分别进行30 次的重复实验,利用30 次仿真实验的RMSE 对不同方法的鲁棒性能进行比较.
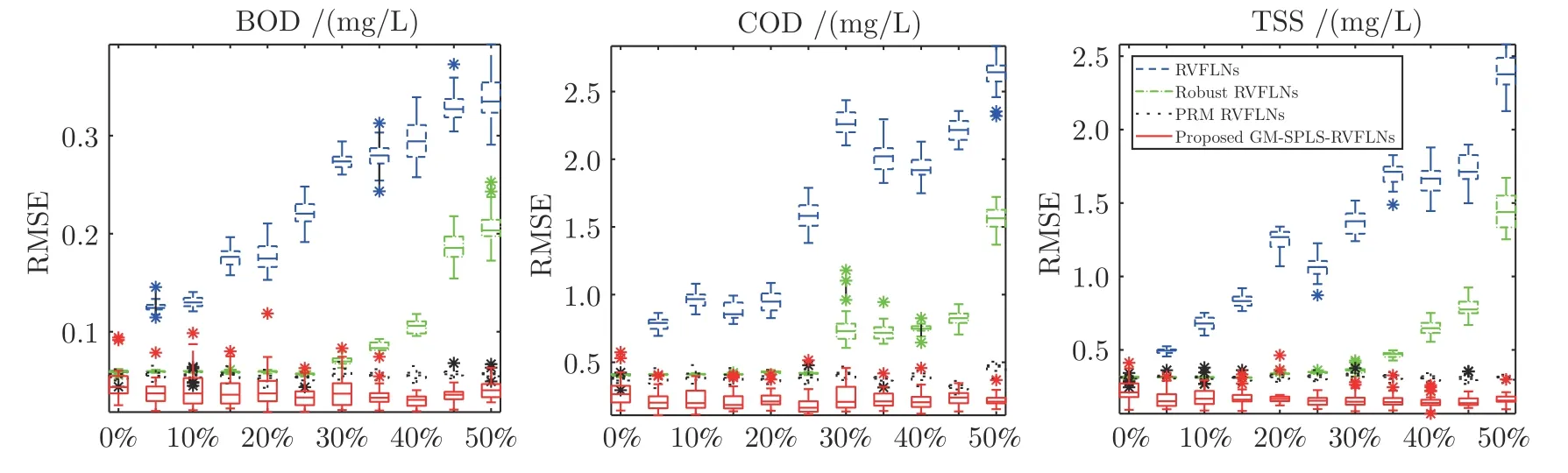
图3 输入样本无离群点输出样本不同比例离群点时的出水水质指标估计RMSE 箱形图Fig.3 The box diagram of the estimation RMSE of effluent quality indices for input sample without outliers and output sample with outliers of different rates
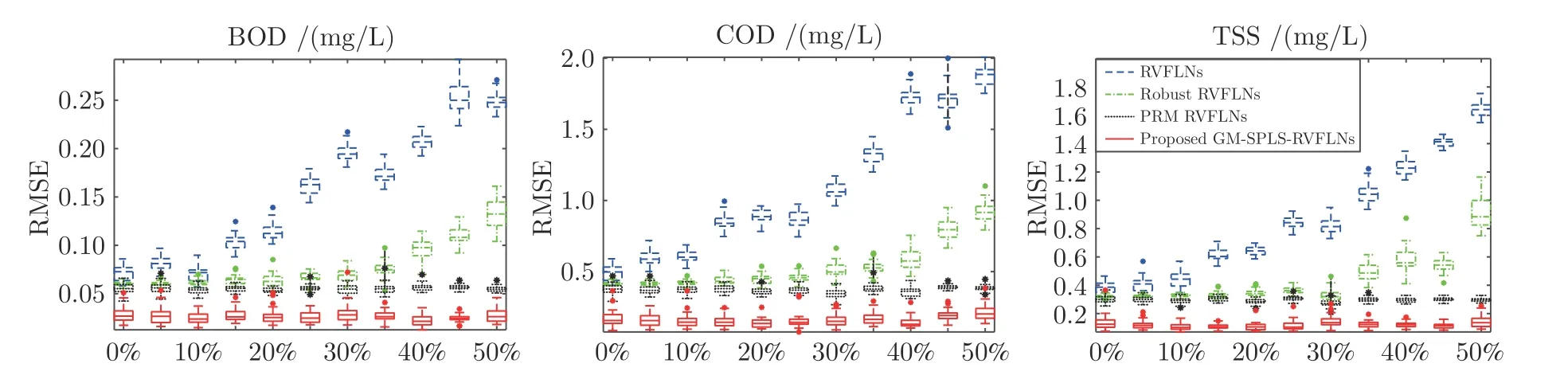
图4 输入样本含5%离群点输出样本不同比例离群点时的出水水质指标估计RMSE 箱形图Fig.4 The box diagram of the estimation RMSE of effluent quality indices for input sample with 5% outliers and output sample with outliers of different rates
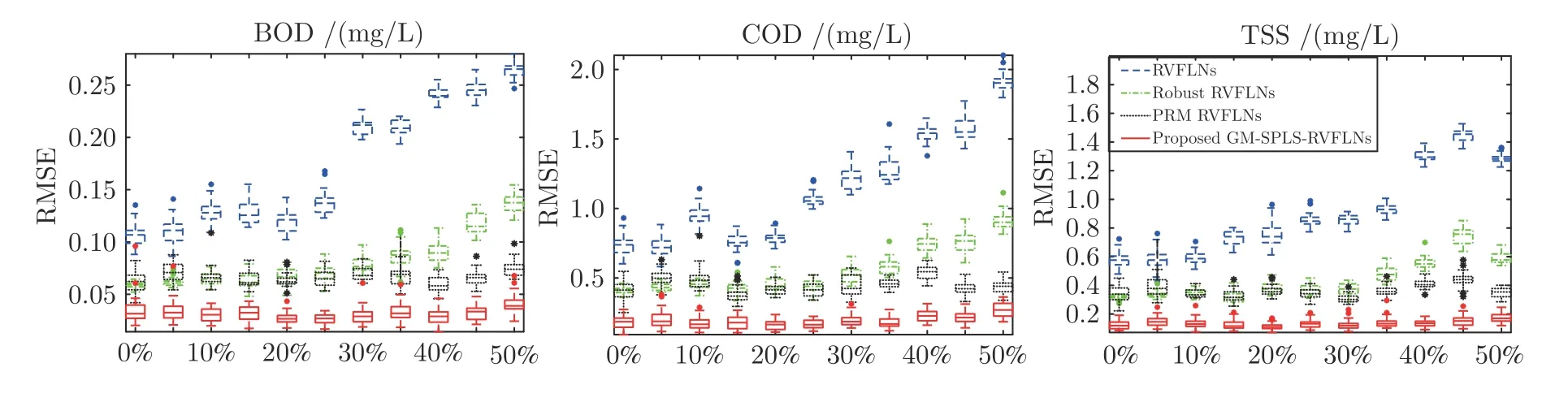
图5 输入样本含15%离群点输出样本不同比例离群点时的出水水质指标估计RMSE 箱形图Fig.5 The box diagram of the estimation RMSE of effluent quality indices for input sample with 15% outliers and output sample with outliers of different rates
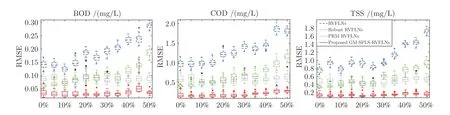
图6 输入样本含25%离群点输出样本不同比例离群点时的出水水质指标估计RMSE 箱形图Fig.6 The box diagram of the estimation RMSE of effluent quality indices for input sample with 25% outliers and output sample with outliers of different rates

图7 输入样本含35%离群点输出样本不同比例离群点时的出水水质指标估计RMSE 箱形图Fig.7 The box diagram of the estimation RMSE of effluent quality indices for input sample with 35% outliers and output sample with outliers of different rates
从图3~7 的箱形图可以看出,当输入输出样本均无离群点或离群点比例较小时,RVFLNs 和Robust RVFLNs 的水质指标估计效果相当,但是两种方法都没有PRM RVFLNs 和所提GM-SPLSRVFLNs 方法的估计精度高,原因在于这两种方法都没有考虑隐含层矩阵的多重共线性问题,导致模型的输出权值产生病态解,进而造成模型的预测误差较大.PRM RVFLNs 虽然利用PLS 减小了多重共线性的干扰,但是其精度也没有所提方法高,因为所提方法利用稀疏偏最小二乘筛选了对模型有用的变量,提高了模型的精度.同时,随着离群点比例的增加,基本RVFLNs 的水质指标模型因缺乏鲁棒性,预测精度明显下降.而Robust RVFLNs 模型利用M 估计增强了模型的鲁棒性,精度好于RVFLNs模型.但是M 估计只是针对输出样本的离群点进行降权处理,不能同时抵挡来自输入端和输出端的离群点,所以当输入样本含有离群点时,模型崩溃,预测精度比较低.PRM RVFLNs 对输入和输出样本都利用了M 估计确定建模权重,因此预测效果比Robust RVFLNs 略好一些,但是效果没有GMSPLS-RVFLNs 明显.只有所提GM-SPLS-RVFLNs水质指标模型利用广义M 估计充分考虑了输入输出样本之间的关系,并且根据隐含层向量在空间的位置和标准化残差大小分别确定输入输出样本的建模权重,使得模型具有更高的鲁棒性,更低的建模误差.
一个好的鲁棒模型要求在实际模型与理想分布模型差别微小时,受离群点的影响较小,接近正确估值,更重要的是要求实际模型与理想分布模型差别较大时,估计值也不会受大量离群点的破坏性影响,依然能够得到接近正常模式下的正确估计[13].因此观察输入输出样本离群点比例均为25%的多元水质指标建模与估计效果.图8 为输入输出样本均含25%离群点时的曲线拟合情况,可以看出本文所提方法的建模效果最好,能够对水质指标进行准确估计,并且估计趋势与实际数据基本一致.图9为输入输出样本均含25%离群点时的实际值与估计值的散点图,可见GM-SPLS-RVFLNs 的估计值比其他方法更接近实际值.图10 为输入输出样本均含25%离群点时的不同方法水质指标测试误差概率密度函数(Probability density function,PDF)分布曲线,可以看出所提GM-SPLS-RVFLNs 的误差PDF 分布曲线呈现出又瘦又高的高斯分布形状,并且整体与 “0” 纵轴基本重合,表明所提方法的估计误差在概率意义上的均值为0,即利用所提方法建立的水质指标模型估计值与实际值之间的误差比较小.
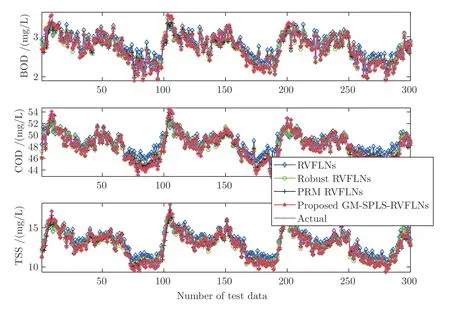
图8 输入输出样本均含25%离群点时,不同方法出水水质指标建模效果Fig.8 Modeling results of effluent quality indices with different methods for input and output samples with 25% outliers

图9 输入输出样本均含25%离群点时,不同方法水质指标散点图Fig.9 The scatter plot of effluent quality indices with different methods for input and output samples with 25% outliers
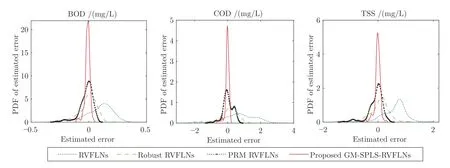
图10 输入输出样本均含25%离群点时,不同方法水质指标估计误差PDF 曲线Fig.10 The PDF curve of effluent quality indices estimation error with different methods for input and output samples with 25% outliers
由于在离群数据建模时,模型鲁棒性好,建模精度就高,反之会存在较大的建模误差.为此,进一步采用常见的建模误差性能指标对几种水质指标建模方法的估计误差进行直观比较,如表2 所示.对于均方根误差(RMSE)指标和平均绝对百分比误差(Mean absolute percentage error,MAPE)指标而言,其数值越小,说明模型的数据拟合能力越好,因而模型估计性能越优良,且对于离群数据的鲁棒性能越高.而对于R 平方指标而言,其数值越接近1,说明模型拟合数据的能力越强,可以对水质指标进行准确估计,且对于离群数据的鲁棒性越好.通过表2 各项性能指标数据的综合对比分析可以看出,本文所提GM-SPLS-RVFLNs 水质指标建模方法的鲁棒性和预测精度最高.

表2 输入输出样本均含25%离群点时,不同水质指标建模方法性能指标对比Table 2 The comparison of performance indexes of effluent quality indices with different methods for input and output samples with 25% outliers
最后,为了验证所提算法的水质参数模型的稀疏性,利用输出权值中所含 “0” 的个数进行比较.由于PRM RVFLNs 模型是在RVFLNs 的基础上改进的,并没有进行稀疏化处理,所以PRM RVFLNs模型与RVFLNs 模型的稀疏性一样,因此本文只比较PRM RVFLNs、Robust RVFLNs 和GM-SPLSRVFLNs 模型的稀疏性,结果如图11 所示.可以看出,所提GM-SPLS-RVFLNs 模型的输出权值中含 “0” 的个数最多,模型的稀疏性最好.PRM RVFLNs 模型的稀疏性最差,而Robust RVFLNs模型由于弹性网罚的作用有着较好的稀疏性,但是没有所提方法的稀疏性稳定,并且输出权值中含 “0”的个数也没有本文方法多.这说明,本文所提方法利用SPLS 算法,可以有效地增强模型的稀疏性,使得与输出变量无关的隐含层变量不参与计算,从而提高了模型的计算效率和泛化能力.

图11 输入输出含不同比例离群点时,不同建模方法的输出权值中所含 “0”的数量曲线Fig.11 The curve of the number of output weights with ‘0’ value with different methods for input and output samples with outliers of different rates
4 结论
本文针对污水处理过程多元水质指标难以在线检测的难题,基于稀疏偏最小二乘回归(SPLS)和Schweppe 型广义M 估计技术,提出一种新型的RVFLNs 稀疏鲁棒建模方法,并应用到污水处理过程的水质指标在线预测中.数据实验表明:当输入输出样本数据的离群点比例较小时,所提GMSPLS-RVFLNs 水质模型因考虑了隐含层矩阵的多重共线性问题,因而比基本的RVFLNs 模型和利用弹性网罚的Robust RVFLNs 模型有着更低的建模误差.随着输入输出样本的离群点比例增加,GMSPLS-RVFLNs 模型利用Schweppe 型广义M 估计充分考虑了输入输出样本之间的关系,对离群点进行合理处理,与RVFLNs、Robust RVFLNs 和PRM RVFLNs 方法相比有更低的预测误差.综上,所提GM-SPLS-RVFLNs 模型利用SPLS 和Schweppe 型广义M 估计不仅有效解决了多重共线性和鲁棒性差的问题,同时还提高了模型的计算效率和建模精度,并且为其他类似的复杂工业难建模问题提供了参考方案.

