一种基于邻域粒度熵的离群点检测算法

段 珣，杨志勇，江 峰

(青岛科技大学信息科学与技术学院，山东 青岛 266061)

0 引 言

离群点是数据集中显著区别于其他数据对象的一小部分数据对象，这部分对象不符合数据集的一般模型。在信用卡欺诈检测、网络入侵检测、故障诊断、医疗诊断等诸多领域中，离群点检测技术都可以发挥重要作用。离群数据并不等同于错误数据，其出现往往隐含或预示着某种具有特殊意义的事件或现象。与分类、聚类等数据挖掘技术相比，离群点检测可能更加有用，因为1万条正常的记录可能只覆盖一条分类规则，而10个离群点可能就蕴含着10条有用的规则。例如，如果将离群点检测应用于入侵检测，那么10个离群点可能就代表10个入侵，而将其应用于信用卡欺诈检测，那么10个离群点可能就代表10起信用卡盗用事件。

离群点检测最早出现在统计学领域，现有的离群点检测方法主要分为：基于统计的检测方法[1]、基于距离的方法[2]、基于密度的方法[3]、基于聚类的方法[4]、基于粗糙集的方法[5]。

已有的离群点检测方法大多假设所处理的数据是确定和完备的，而现实生活中又存在着很多的不确定与不完备数据。为了处理这类数据，研究者提出了一系列基于粗糙集的离群点检测方法[2,5-7]。自1982年Pawlak[8]提出粗糙集理论以来，粗糙集已经成为处理不确定性、不完备性的重要工具。基于粗糙集的离群点检测方法获得了广泛关注。然而经典的粗糙集模型不适合于直接处理数值型数据。为了从数值型数据中检测离群点，已有的基于粗糙集的离群点检测方法通常需要对数值型数据进行离散化处理。离散化过程很容易导致信息的丢失，从而影响到后续的离群点检测的整体性能。

针对经典的粗糙集模型在处理数值型数据上所存在的困难，有必要考虑采用扩展的粗糙集模型来进行离群点检测，例如，采用邻域粗糙集模型来检测离群点。邻域粗糙集模型最早由Hu等[9-11]所提出。作为经典粗糙集模型的一种有效扩展，邻域粗糙集能够直接处理数值型数据，从而避免了离散化过程所带来的信息丢失问题。

基于上述考虑，本文利用邻域粗糙集模型来检测离群点。具体而言，在邻域粗糙集中引入一种新的信息熵模型——邻域粒度熵。通过使用邻域粒度熵，可以有效度量论域U中各个对象之间的差别，从而检测出其中所存在的离群点。

为了解决信息的量化度量问题，Shannon[12]在1948年首次提出信息熵的概念。近年来，信息熵已被扩展到邻域粗糙集中，并由此出现了一些新的信息熵模型。Hu等人[13]将信息熵概念拓展到邻域粗糙集中，提出了邻域信息熵的概念。在文献[14]中，Chen等人进一步发展了邻域信息熵理论，提出了一种基于邻域信息熵的不确定性度量方法。目前，邻域信息熵已被用于解决属性约简、规则获取等实际问题[15]。但是，利用邻域信息熵来进行离群点检测的研究尚不多见。因此，开展基于邻域信息熵的离群点检测研究是非常有必要的，不仅可以解决经典的粗糙集模型在处理数值型数据上所存在的困难，而且还可以进一步拓展邻域信息熵的应用范围。

基于邻域粒度熵，本文提出一种新的离群点检测算法OD_NGE。通过在多个公共数据集上的实验表明，OD_NGE算法的性能要优于已有的离群点检测方法。

1 基本理论

邻域粗糙集中NS=(U,A,V,f,δ)为一个邻域信息系统，其中，U={x1,x2,…,xn}是论域，表示对象的集合；A是属性集；V=∪a∈AVa是值域，Va是单个属性a的值域；δ表示邻域半径参数；f:U×A→V表示映射函数，即对任意x∈U以及a∈A，有f(x,a)∈Va。对任意x∈U和属性子集B⊆A，对象x在属性子集B上的邻域类为[9-11]：

B在论域上的邻域关系被定义为[9-11]：

对任意x,y∈U和属性子集B⊆A，对象x、y在属性子集B下的距离度量及邻域半径的确定采用文献[16-17]的方法。

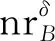
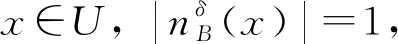
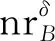
2 邻域粒度熵与邻域粒度熵离群因子

从定义3可以看出，邻域粒度熵提供了一种更加全面的不确定性度量机制，它将邻域信息熵和邻域知识粒度这2个概念融合在一起，其中前者可以刻画邻域知识的完备性，而后者则可以刻画邻域知识的粒度大小。

接下来，利用邻域粒度熵来计算论域U中每个对象的相对重要性，对象的相对重要性将被用于后续的离群点检测任务。

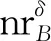
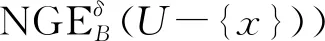
除了对象的相对重要性，本文在检测离群点时还考虑到“相对比重”和“基于相对势的异常度”这2个因素。

其中，min和max分别表示|N1|、|N2|、…、|Nq|中的最小值和最大值。

相对比重刻画了对象x所在的邻域类(即群体)的规模。由于离群点属于数据集中的一小部分对象，因此，对象所在的邻域类的规模在一定程度上可以反映其离群的程度，即x所在的邻域类的规模越大，则表明数据相对集中，x成为离群点的可能性就越低。

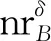
通过引入基于相对势的异常度，进一步放大了不同邻域类的规模对离群点检测结果的影响。

定义8 邻域粒度熵离群因子。给定邻域信息系统NS=(U,A,V,f,δ)，其中，A={a1,a2,…,ap}，对任意对象x∈U，对象x的邻域粒度熵离群因子NGEOF(x)被定义为：

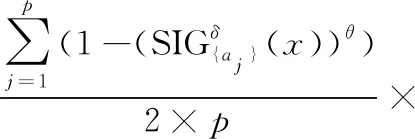
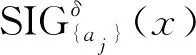
定义9 基于邻域粒度熵的离群点。给定邻域信息系统NS=(U,A,V,f,δ)，令μ为一个给定的阈值，对任意x∈U，如果NGEOF(x)>μ，则对象x被称为NS中的一个基于邻域粒度熵的离群点，其中NGEOF(x)为对象x的邻域粒度熵离群因子。

3 基于邻域粒度熵的离群点检测算法OD_NGE

OD_NGE算法的流程如图1所示。

如图1所示，OD_NGE算法首先读取数据集并将离群点集合置为空集；其次，针对数据集中每个属性计算邻域覆盖；第3，针对每个属性，计算其邻域粒度熵；第4，计算论域U中每个对象x的重要性、相对比重、相对势及异常度；第5，将第4步所得数值进行集成计算，得到对象x的离群因子；第6，如果对象x的离群因子大于给定阈值，则将x放入离群点集合；最后，将离群点集合输出。

OD_NGE算法的伪代码如下：

输入：NS=(U,A,V,f,δ)，其中U={x1,x2,…,xn},A={a1,a2,…,ap}；参数θ，阈值μ。

输出：U中的离群点集合O。

Step1将离群点集合O初始置为空集。

Step2对任意属性aj∈A, 1≤j≤p，循环执行下列语句：

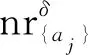
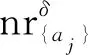
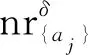
Step3对任意对象xi∈U, 1≤i≤n，循环执行下列语句：

Step3.1对任意属性aj∈A, 1≤j≤p，循环执行下列语句：

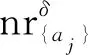
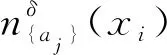
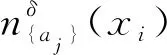
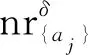
Step3.2根据定义8与Step3.1所得数据计算对象xi的邻域粒度熵离群因子NGEOF(xi)。

Step3.3如果NGEOF(xi)>μ，则将对象xi加入离群点集合O中。

Step4返回离群点集合O，算法结束。

4 实验结果与分析

下面，通过实验来验证OD_NGE算法的离群点检测性能。对比算法包括：KNN (K-Nearest Neighbor)[19]、NED (Neighborhood Outlier Detection)[20]、NVDMOD (Neighborhood Value Difference Metric-based Outlier Detection)[6]和SMAOD (Sequence-based Mixed Attribute Outlier Detection)[7]算法。在上述4个对比算法中，KNN属于传统的基于距离的离群点检测方法；NED是一种邻域半径直接给定的邻域离群点检测方法；NVDMOD是一种基于邻域值差异度量的离群点检测方法；SMAOD是一种基于序列的离群点检测方法。

不同算法的参数设置情况如下：首先，关于OD_NGE算法的参数设置，通过多次实验来逐步调节参数θ的值，并选择能够获得最优实验结果的参数值，最终，将参数θ的值设置为0.55。其次，对于4个对比算法，它们也包括一些需要提前设置的参数。这4个对比算法的每个参数均根据相关文献中所提供的参数值来进行设置[6-7,19-20]。

为了对比不同算法的离群点检测性能，本文使用目前最常用的一类评价标准。该评价标准的主要思路如下：为了判断一个离群点检测算法的性能好坏，在多个数据集上运行该算法，并计算该算法找到的离群点中属于真正离群点的比例。这个比例越高，则说明该算法的离群点检测性能越好。

实验数据集包括：Breast Cancer和Lymphography，其中，Breast Cancer是一个数值型数据集，而Lymphography则是一个符号型数据集[21]。

首先在Breast Cancer数据集上进行实验。该数据集包括699个样本和9个数值型属性。所有样本被分为2大类：begin(占比65.5%)和malignant(占比34.5%)。为了便于实验，本文随机选择一部分malignant类别的样本，并将其删除。最终的Breast Cancer数据集包含483个样本，其中，有39个样本属于malignant类，另外444个样本则属于begin类[22]。

不同算法在Breast Cancer数据集上的离群点检测结果如表1所示。

实验中，对于每个离群点检测算法，根据由该算法所求出的所有样本的离群程度值，将所有样本进行降序排序。所以，在表1中，“离群程度值前k%的样本(样本个数)”是指在采用某个算法求出所有样本的离群程度值之后，离群程度值排在前k%的样本以及这些样本的个数。另外，“属于离群点的样本个数”是指离群程度值排在前k%的样本中，真正属于离群点的样本个数，“覆盖率”是指真正属于离群点的样本个数占离群点总数的比例[23]。

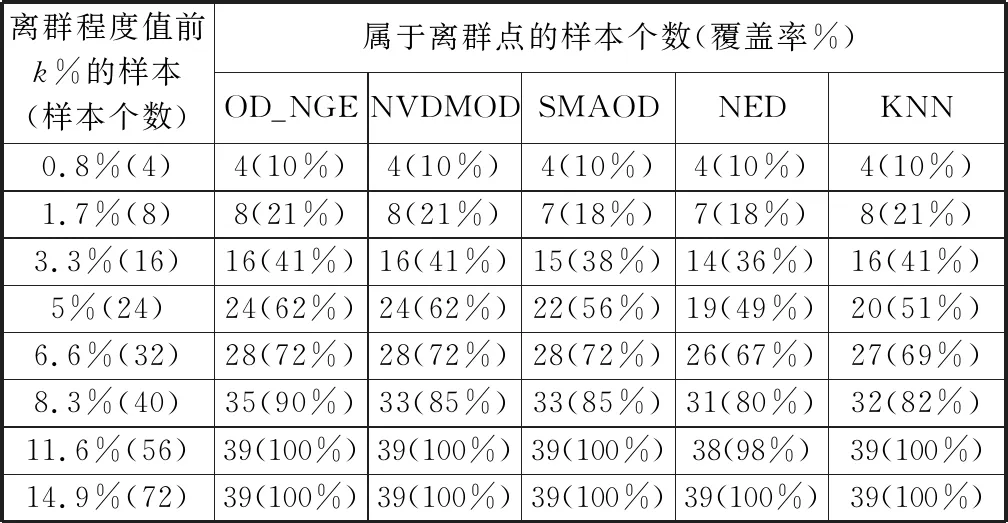
表1 Breast Cancer上离群点检测结果

从表1可以看出，在Breast Cancer数据集上，OD_NGE与NVDMOD这2个算法的离群点检测性能比较接近，它们的性能要显著优于另外3个算法(即SMAOD、NED和KNN)，此外，OD_NGE算法的性能要略优于NVDMOD算法。当分析离群程度值前k%的样本时，OD_NGE算法所检测出的真正的离群点个数以及覆盖率总是最高的。例如，分析离群程度值前5%的样本时(合计有24个样本)，OD_NGE算法和NVDMOD算法所检测出的真正的离群点有24个，即由OD_NGE和NVDMOD所找出的24个离群点都是真正的离群点，没有出现任何误判，而SMAOD、NED和KNN算法分别只找到了22、19和20个真正的离群点，即这些算法分别出现了2、5和4次误判。另外，分析离群程度值前8.3%的样本时(合计有40个样本)，OD_NGE算法所检测出的真正的离群点有35个，即由OD_NGE算法所找出的40个离群点中有35个是真正的离群点，即只出现了5次误判，而NVDMOD、SMAOD、NED和KNN算法分别只找到了33、33、31和32个真正的离群点，即这些算法分别出现了7、7、9和8次误判。

接下来，本文在Lymphography数据集上进行实验。该数据集包括148个样本，这些样本由18个条件属性和1个决策属性来描述。所有样本被分为4类：normal find (占比1.35%)、metastases (占比54.73%)、malign lymph (占比41.22%)、fibrosis (占比2.7%)。将Lymphography数据集中属于normal find和fibrosis类的样本看作是离群点，因此，该数据集中总共有6个离群点。

不同算法在Lymphography数据集上的离群点检测结果如表2所示。

需要指出的是，Lymphography数据集所包含的离群点数量较少，而且大部分算法都能在离群点比例较低时就能够检测出所有的离群点。例如，当离群点比例在10.1%时，大部分算法都已经检测出所有的离群点。为了展示出不同算法在检测出每一个新的离群点时所对应的离群点比例，因此，在表2中，离群点比例的等级划分设置较密。

表2 Lymphography上的离群点检测结果

从表2可以看出，在Lymphography数据集上，OD_NGE与SMAOD这2个算法的离群点检测性能相同，它们的性能要显著优于另外3个算法(即NVDMOD、NED和KNN)。分析离群程度值前k%的样本时，OD_NGE算法所检测出的真正的离群点个数以及覆盖率总是最高的。例如，分析离群程度值前4.7%的样本时(合计有7个样本)，OD_NGE算法和SMAOD算法所检测出的真正的离群点有5个，即由OD_NGE和SMAOD所找出的7个离群点中有5个是真正的离群点，只出现了2次误判，而NVDMOD、NED和KNN算法都只找到了4个真正的离群点，这些算法都出现了3次误判。

综合Breast Cancer和Lymphography这2个数据集上的实验结果来看，OD_NGE算法的离群点检测性能要优于NVDMOD、SMAOD、NED和KNN这4个现有的算法。

5 结束语

近年来，基于粗糙集的离群点检测方法得到了广泛应用，很多基于粗糙集的离群点检测方法被提出[24-26]，且在入侵检测[27]、信用卡欺诈检测等方面有着实际的应用，被很多商业公司提上了议事日程[28]。但是，由于经典的粗糙集模型不适合于直接处理数值型数据，因此需要对数值型数据进行离散化处理，而离散化过程又会导致信息的丢失。因此，如何利用粗糙集的方法从数值型数据中检测离群点就成为该领域的一个关键问题。针对上述问题，本文基于邻域粗糙集来检测离群点，在邻域粗糙集中提出了一种新的信息熵模型——邻域粒度熵，并基于该模型设计了一种新的离群点检测算法OD_NGE。实验结果表明，OD_NGE算法能够从数值型数据中有效地检测出离群点。

在下一步的工作中，计划将本文所提出的离群点检测算法应用于网络入侵检测中，即通过将入侵行为看作是偏离于正常行为的离群点，从而把离群点检测作为一种无监督的入侵检测方法而应用于入侵检测。