基于高性能计算的离散介质冲击过程
吴志平,刘波平,王 康,李石滨,胡毕炜,胡必伟,游 杰
(江西省科技基础条件平台中心,江西 南昌 330003)
0 引 言
散体介质广泛分布于沙漠、海洋、矿山等自然界[1-3],也被应用于化学和生物领域[4-6]或工业装备的减震隔振[7-9]等领域。其分布甚至不局限于地球。在行星探测领域,月球表层土壤、火星土壤等均为散体介质。随着我国对月球及火星探索工作的开展,在探测器降落月球或者火星表面的过程中,无论是发动机吹起的表面土壤的过程,还是探测器支撑脚与火星或月球土壤之间的冲击行为,都存在与散体介质的相互作用,也涉及各种离散介质间的冲击过程,因此对离散介质冲击问题的研究具有重要意义[10-11]。对于大规模颗粒介质的模拟,例如:对流化床[12-14]、风沙流[15]的模拟最常用的方法是基于高性能计算平台的离散元模拟,在上述模拟过程中,颗粒的恢复系数是一个重要的参数。
为了对离散介质冲击过程进行精确描述,本文对离散介质冲击过程的速度变化过程进行模拟,研究离散介质冲击过程恢复系数的变化规律。关于这个课题已有相当多的研究,对离散介质冲击过程中动力学行为给出了较为细致的分析,如模型选取[16-17]和链长度对结果的影响[18-19]等。Liu等[18]在定义了接触模型的基础上,将对时间的积分转换为对冲量的积分,解决了因时间步长的选取造成的计算量过大以及精度问题。此外,Gharib等[19]发现,一组不同粒径的链在不同排布下,其冲击过程会产生显著差别。但在上述研究中,很少关注不同直径的离散介质冲击过程的宏观统计规律,如恢复系数的统计规律对离散介质冲击过程的影响。
基于高性能计算平台的仿真模拟是科学研究的重要方向,特别是对离散介质这类数量十分庞大的物质,其模拟研究必须借助超级计算机等高性能计算平台进行。李勇俊[20]使用高性能计算平台对离散介质堆积生成进行研究,Gan等人[21]对工业生产中的大颗粒搬运、Herman等人[22]对离散介质搅拌等领域使用高性能计算平台进行了模拟。Yue等人[23]使用高性能计算平台对颗粒填充过程进行了模拟。刘丽芝等人[24]使用高性能计算平台对离散介质的冲击过程进行模拟。此外,流体与离散介质的耦合过程也是研究的重点,高性能计算平台在该领域也得到了重要的应用[25]。
但是,使用高性能计算平台对颗粒链冲击过程进行模拟较为少见,特别是对多分散颗粒链的统计研究更为罕见。因此,本文通过使用高性能计算平台进行并行计算,研究单分散链、多分散链与入射介质末速度、恢复系数与压缩阶段冲量的变化规律,以及与传统恢复系数的对比。
1 接触模型和计算模拟方法
1.1 冲击过程的动力学模型
图1所示为一维离散颗粒链,由n个相同材料的均质颗粒紧密排列构成,由左至右依次编号为1~n,所有颗粒的质心在一条直线上。初始状态下,颗粒之间恰好相互接触但无相互作用力。编号为1的颗粒为碰撞颗粒,即入射颗粒,编号为2~n的颗粒组成颗粒链的其余部分。这里颗粒链的半径考虑为单分散和高斯分布多分散2种情况,当考虑颗粒链为单分散分布时,入射颗粒的半径与颗粒链其余颗粒的半径相同。入射颗粒的初始速度为v1=v0,其余颗粒初始状态下都静止。
参照离散单元法(DEM),颗粒只与其两侧与之接触的颗粒产生相互作用。设任一个颗粒i的质量、粒径、速度和位置分别为mi、Ri、vi以及xi,相邻颗粒对颗粒i的接触力为Fi-1,i和Fi,i+1,其中入射颗粒只受到颗粒链中颗粒2向左的作用力,而颗粒链最右端的颗粒n只受到它左侧颗粒n-1向右的作用力。因此颗粒链中每一个颗粒的离散牛顿动力学方程组为:
(1)
(2)
(3)
对于颗粒与颗粒之间的接触力,存在多种通过压缩量、相对速度等参数定义的接触力模型[26],这里采用Thornton模型[27]计算:
(4)
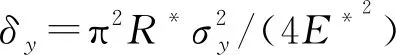
δp,q=Rp+Rq-|xp-xq|
(5)
vp,q=vq-vp
(6)
以颗粒链左端为坐标原点建立坐标系,因此各颗粒的初始条件为:
(7)
(8)
当颗粒链中的每一个颗粒均与其余颗粒不发生接触,并且所有颗粒之间相互远离:
δi,i+1<0,vi (9) 即所有颗粒都在相互远离,便可认为颗粒链的冲击过程结束。通过上述方程和条件,就可以模拟颗粒与一维颗粒链的碰撞过程。 对于恢复系数,有2种常用的定义,一种是基于碰撞前后的相对速度之比,其定义如下: (10) (11) 其中,pc、pf分别为碰撞过程中,2个颗粒压缩阶段和恢复阶段的冲量。对于2个颗粒对心正碰,eN和eP完全等价。 以聚四氟乙烯(PTFE)为例,采用数值模拟研究不同入射颗粒的初速度、入射颗粒与颗粒链颗粒半径的粒径比、颗粒链长度等情况下,入射颗粒的回弹速度、颗粒链颗粒的末速度、颗粒之间的碰撞恢复系数、能量耗散率等结果的变化规律。该材料的参数如表1所示。 表1 PTFE的部分力学参数 这里假设聚四氟乙烯PTFE是一种完全的粘弹性材料,遵循完全的弹塑性压缩和恢复过程。为确保足够的精度,本文所有模拟中的时间步长均为1.0×10-9s。 在确定了时间步长、材料参数和颗粒的粒径分布形式,接触模型以及其他必须变量之后,便可以对整个碰撞过程进行模拟。图2给出了本文模拟过程的流程图。 碰撞颗粒的半径是影响入射颗粒碰撞后速度的关键因素。实际颗粒系统中,即便颗粒链中颗粒个数和大小不变,但是因为不同大小颗粒的排列不同,导致与入射颗粒碰撞的颗粒的半径不同,因此入射颗粒碰撞后的速度有所不同。为了描述这种情况导致的入射颗粒碰撞速度的变化,下面模拟不同种颗粒排列下入射颗粒碰撞速度分布和对不同粒径分布下的冲击过程。由于计算量较大,基于现有超算平台的多个高性能计算节点以及MPI并行算法库,对颗粒链冲击过程的算法进行并行化处理,将计算任务分配到各个从节点上,并通过MPI算法库将所有从节点进程的计算结果汇总到主节点上,最后对数据结果进行统计。本文所使用模拟程序的伪代码段如算法1所示。 算法1 模拟过程的伪代码。 Algorithm: Discrete Material Chain Impact Require: equation (7), equation (8) and necessary parameters // Initialization of MPI MPI_Init() MPI_Comm_size() MPI_Comm_rank() do i=myid,n,numprocs // n is the times of simulation initialization of the chain sp←true// the sign of the end of the impact while sp is true //the main procedure of the impact in different process use the equation (5) and equation (6) to get the compressions and relative velocities get the contact force by equation (4) use equation (1)-equation (3) to update the locations and the velocities use the equation (9) to determine whether the sign sp is true end while aggregate the data to the main process (process0) using MPI_Gather() MPI_Barrier() //interprocess synchronization end do If myid=0 // all of statistics were on main process count the data and output results in process0 end if MPI_Finalize( ) 基于高性能计算平台,本文采用独立开发的离散介质冲击过程模拟程序,对整个冲击过程进行模拟。 下面,研究给定不同入射初速度、颗粒链粒径分布、颗粒链长度等情况下,由PTFE组成的颗粒与一维颗粒链碰撞后颗粒链中颗粒的速度,研究入射颗粒碰撞恢复系数、颗粒链能量留存率。颗粒的质量根据材料密度和颗粒的半径计算。 首先为了验证使用的程序的准确性,本文对比了不同入射速度下,2个颗粒对心碰撞恢复系数的模拟结果与理论结果。如图3(a)的对比结果可知,本文所使用的模拟程序有着较高的精确性,其误差在1%以下,能准确模拟整个弹塑性Thornton接触过程。之后,本文模拟了颗粒与颗粒链碰撞后,各颗粒碰撞速度随时间变化,如图3(b)所示。颗粒链的长度为10,单分散颗粒链颗粒的半径为150 μm;多分散颗粒链颗粒的半径服从正态分布,均值为150 μm,标准差为30 μm。如图3所示,碰撞结束后,颗粒链中每一个颗粒的速度最终都会达到稳定,并且颗粒的速度在达到稳定后都呈现依序号递增的状态,该结果与Liu等人[18]的模拟结果相似,验证了本文算法的准确性。 (12) 图3显示,颗粒与颗粒链碰撞后速度最终达到稳定,但由于碰撞过程中能量损失,颗粒链长度对入射颗粒末速度有一定影响。同时,将入射颗粒的泊松恢复系数随颗粒链长度变化绘制于图4(a),显示入射颗粒的碰撞恢复系数随着颗粒链长度增加而增大。当颗粒链长度大于7时,入射颗粒的泊松恢复系数不再改变,保持稳定,并且入射颗粒在压缩阶段的冲量pc不随颗粒链长度的变化而变化,见图4(b),其中Δv=pc/m1为压缩阶段的速度变化量。 对于不同粒径分布下的情况,分别将统计结果绘制于图5。从图5(a)可以看出,入射颗粒与多分散颗粒链碰撞后的速度应该与颗粒链不同大小的颗粒排列相关,因为不同大小颗粒随机排列,导致入射颗粒碰撞后速度的方向可能与原来速度相同,也可能相反。其次,入射颗粒碰撞后的速度分布较宽,类似于正态分布,随着模拟次数的提高,这个分布已经稳定,因此后续关于多分散颗粒链碰撞恢复系数等研究,都要通过多次碰撞模拟,计算入射颗粒的平均碰撞速度和标准差。图5(b)~图5(c)分别是多分散颗粒链中入射颗粒碰撞速度分布受初始速度的影响以及受入射颗粒与被碰撞颗粒半径比的影响。由图5(b)可知,初始速度越大,入射颗粒碰撞后速度分布越宽且平均速度越大。给定入射颗粒初始速度以及粒径比R2/R1,碰撞结束时入射颗粒的末速度分布近似于正态分布。从图5(c)可以很明显地看出,当粒径比大于1.4时,碰撞后的入射颗粒末速度分布集中于很小的一个范围内。由此可推测,当颗粒链颗粒总被碰撞颗粒尺寸远大于入射颗粒尺寸时,即R2/R1≫1.0,入射颗粒的末速度将近似于2个颗粒碰撞的情形。 图5(d)比较了2个颗粒碰撞与颗粒链碰撞的eP随半径比变化情况。从图5(d)可以看出,R2/R1≤1.2时,2个颗粒碰撞情形与一维颗粒链碰撞情形下的eP差异较大,而当R2/R1>1.4时,2种情形下eP趋于一致。这表明,当粒径比R2/R1>1.4时,入射颗粒与颗粒链碰撞可近似为2个颗粒碰撞。 接下来,给定相同的初始速度,对比单分散和多分散链的冲击过程。入射颗粒eP随初始速度的变化规律,如图6所示。同时与无限大半空间的碰撞结果也绘制于图6。由图6(a)可以看出,相较于传统恢复系数即颗粒与无限大半空间的冲击后的速度比,单分散链与多分散链的泊松恢复系数eP差别不大,特别是在入射速度增加时,差别可以忽略,且大于传统冲击过程的恢复系数。如图6(b)所示,入射颗粒的末速度远小于与无限大半空间冲击的情况。这说明链对入射颗粒的能量耗散要显著强于与无限大半空间碰撞。其原因是入射颗粒与链的冲击过程中,所受到的冲量大于与无限大球的碰撞过程,因而能量耗散更高。这从理论上验证了离散介质在抗振减振方面的显著效果。 基于高性能计算平台,本文研究算法1所给出的并行算法的效率。图7对比了不同颗粒链长度下,模拟1000次在不同核数下的加速比和并行效率。图7(a)展示了上述条件下的加速比,随着核数的增加,本文所使用的并行算法的加速比基本上呈线性变化。在核数增加到20核情况下,如图7(b)所示,本文并行算法的并行效率保持在88%左右,显示了较好的并行效率。 基于高性能计算平台,本文模拟了牛顿摆,即单个颗粒冲击无边界颗粒链的过程,对不同入射速度、颗粒链尺度分布条件下,颗粒链中颗粒的速度变化规律特别是入射颗粒的碰撞后速度进行了详细分析。发现入射颗粒与颗粒链碰撞后,颗粒链中各个颗粒的速度最终将保持不变;泊松恢复系数在颗粒链长度较小时,随颗粒链长度增长而增大,最后趋于稳定。而入射颗粒压缩阶段的冲量不随颗粒链长度的增长而变化,只与入射速度线性相关。对于多分散颗粒链,当被碰撞颗粒与入射颗粒的半径比大于某一个值时,入射颗粒冲击颗粒链的泊松恢复系数与2个颗粒的碰撞基本相等,可以忽略颗粒链后续颗粒对入射颗粒碰撞速度的影响,这个值与冲击速度和材料参数相关,比如冲击速度3 m/s的PTFE颗粒,这个值是1.4。对于颗粒与多分散颗粒链的冲击过程,入射颗粒的末速度分布与初速度和粒径比相关,且分布呈现正态分布形式。本文使用高性能计算平台对颗粒链的冲击过程进行模拟和统计分析,并给出了不同核数下并行效率和加速比的变化关系,结果显示,本文并行算法具有较好的并行效率。 本文验证了对离散介质的冲击过程,其厚度只需要7~8层,之后的颗粒不会对冲击过程产生显著影响,可以大幅减少诸如流化床在内的各种离散介质的计算量。并且,根据本文的计算结果,对于多分散一维离散介质的冲击过程,可以基于高斯分布的概率分布,而非通过传统的数值模拟描述其冲击过程,极大地简化了模拟离散介质冲击过程所需要的计算量。1.2 计算模拟方法

2 结果与讨论
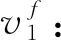

3 结束语

