一种太阳能集热系统集热量实时预测的混合建模方法

刘 慧，丁绪东，杨东润，张 迎，刘忠晨，孙 梅

(山东建筑大学信息与电气工程学院山东省智能建筑技术重点实验室，山东 济南 250101)

0 引 言

现代工业的迅猛发展，大量消耗着地球有限的资源，人类面临着日益严重的能源危机，因此，保护能源、节约能源，成为关系到人类生存和发展的首要问题。在化石燃料日趋减少的情况下，太阳能已成为人类使用能源的重要组成部分，并不断得到发展。太阳能集热器是太阳能利用设备中的重要组成部件，建立简单而又精确的太阳能集热系统模型对太阳能设备利用的优化运行调度至关重要，不仅有利于太阳能的充分利用，还可以提高整个系统的运行效率。为此，大量的研究人员对太阳能集热系统的建模进行了广泛研究。目前，太阳能集热系统的建模方法主要包含机理建模、经验建模和混合建模几种形式。

机理建模方法是从能量守恒的角度出发，根据太阳能集热系统基本的传热机制建立模型的方法，可以实现集热系统采热、传热和换热过程的全局描述。何梓年等[1]通过对热管式真空管太阳能集热器的热性能研究，对热损失、传热系数、传导热阻等作了假设，得到了真空管太阳能集热器的总热损系数、效率因子、热转移因子的计算方法。张小粉等[2]对热超导管作传热管的全玻璃真空管太阳能集热器的传热机理进行了分析，给出了其总热损失系数、效率因子、热迁移因子和瞬时效率的表达式。闫素英等[3]针对玻璃真空管内插热管式太阳能集热器的结构特点、非稳态效率进行了研究，通过能量平衡分析和实验对比，得出较为理想的非稳态效率方程。安玉娇等[4-6]提出U型真空集热管内增加波浪式铝翼以强化传热，建立了U型真空集热管的传热模型和能量平衡方程。葛众等[7]通过对直通式太阳能真空管传热模型的分析，对对流传热损失、真空管厚度及沿厚度方向上的温度差异、集热管状态等做了假设，在导出单根带翅片与不带翅片的直通式太阳能真空管的总热损失系数、效率因子、热迁移因子和瞬时效率的基础上，建立了直通式太阳能真空管的性能预测模型。刘艳峰等[8]建立相变蓄热U型真空管太阳能集热器三维传热数值计算模型，研究工质流动时相变材料对U型真空管集热器热性能的影响。Li等[9]对热损失系数、集热器上的灰尘、集热器背面吸收的辐射等做了假设，建立了强制循环太阳能热水系统中全玻璃真空管集热器的传热模型。Badar等[10]对流体冷却速度、温度传感器和导线质量和热效应等做了假设，对太阳能玻璃真空管集热器的热损失进行了理论的研究。Badar等[11]还对集热器辐射特性、热流条件、入射角对太阳辐射的影响等做了假设，建立了一种分析稳态模型，以研究单相流和两相流同轴管式真空管太阳能集热器的热性能且建立了描述不同传热机制和流动条件的方程组，并对其进行离散化和迭代求解。Paradis等[12]建立了两端开口的太阳能真空管在瞬态条件下的一维热模型。考虑了流体质量流量、环境温度、太阳辐射和风速的变化，以上机理建模方法所得的模型在特定条件下精度较高。但是为了简化复杂的建模过程，大量假设条件的引入导致模型在实际应用过程中偏差较大，同时模型中使用的大量经验参数很难适用于各种不同的工况条件，对模型的精度也会产生一定的影响。

此外，很多人对经验建模方法做了大量研究。经验建模方法不需要对研究对象内部机理的深入理解，是利用研究对象输入输出变量的关系建立模型的方法，在复杂的工业过程中应用比较广泛。张义林等[13]基于BP神经网络建立了热管式真空管集热器热性能的预测校正模型。Roberto等[14]利用灰盒辨识模型和动态自适应线性神经网络(ALNN)模型，考虑了系统在动态条件下的辨识方法。利用能量平衡方程，建立了太阳能集热器在瞬态条件下工作的模型。以上采用经验建模方法所获得的模型对训练数据的依赖性较高，当实验数据在训练数据范围内时模型精度较高，神经网络模型的预测性能与其训练的充分性有关，当训练不充分时，其泛化性会变差。

混合建模方法是经验建模和机理建模2种建模方法的有机结合，利用机理建模方法来构造模型的结构，利用训练数据来辨识模型的参数，既充分利用了2种建模方法的优点，又弥补了两者之间的缺陷。李满峰等[15]采用混合建模提出神经网络和数学模型相结合的方法建立了太阳能集热器神经网络模型，并采用遗传算法对太阳能集热器神经网络模型进行优化，提高了仿真模型的预测精度。本文从能量守恒出发，在充分分析太阳能集热系统采热、传热和换热机理的基础上建立其模型结构；利用TRNSYS仿真软件搭建太阳能集热系统的仿真程序，通过修改仿真系统环境参数获取辨识模型所需要的各种工况下的训练数据；最后借用粒子群优化算法作为模型参数辨识的求解方法，利用训练数据获得模型的未知参数。

1 太阳能集热器工作原理与建模

1.1 工作原理分析

太阳能集热系统通常由采热子系统、储热子系统、用热子系统和控制系统4部分构成，如图1所示。为了防止系统低温结冰，整个系统中传热介质采用去离子水。采热子系统由太阳能集热器、采热循环泵、板换和传热介质缓冲箱4部分构成。太阳能集热器负责接收太阳辐射，将收集的太阳辐射能转化为热能，并把热能传递给集热器内的去离子水；采热循环泵P1负责驱动集热子系统内传热介质的循环；板换负责2个子系统的能量交换；传热介质缓冲箱对水压的变化有一定缓冲作用，能保证系统的水压稳定，水泵不会因压力的改变而频繁地开启。储热子系统由储热水箱、板换、储热循环泵P2这3部分构成。储热水箱利用传热介质存储集热子系统传递过来的热能；储热循环泵负责驱动储热子系统内传热介质的循环。用热子系统由储热水箱、用热循环泵P3和用热设备换热器3部分构成。储热水箱内的传热介质在用热循环泵的驱动下进入用热设备换热器内与用热设备的导热介质进行热交换，实现集热系统对用热设备的能量供给。控制系统由控制器和温度传感器构成。在储热水箱内、集热器出口和板换出口等处安装温度传感器，传感器测量的数据传递给控制器，控制器根据不同的温度设定值控制3个循环泵的启停工作，实现能量存储、管道防冻和能量供给的功能。当集热器出口温度大于储热水箱内温度一定数值时，启动P1和P2这2个循环泵，实现热能的存储；当板换出口温度小于设定值时，启动所有的循环泵，实现管道防冻的功能；当水箱内温度大于用热设备需求温度一定数值时，启动循环泵P3，实现集热系统对用热设备的能量供给。

太阳能集热器是太阳能集热系统的核心部件，集热器种类很多，本文选用应用广泛的热管式太阳能集热器[16]进行介绍，其内部结构如图2所示。集热器采用热压封接技术将带有平板翼片的、具有抗冻性能的铜—水热管封装在单层真空管内，由玻璃外管、吸热板、热管、导热块、保温盒和隔热材料组成，其工作原理是：辐射到集热器玻璃管上的太阳能透过玻璃管，传递到内部的金属吸热板上，吸热板负责将太阳辐射能转化成热能传递给热管，热管内的工质受热蒸发汽化，汽化后的工质蒸气上升到热管冷凝段，在较冷的内表面上凝结，释放出蒸发潜热，冷凝后的液态工质依靠自身重力回流到热管蒸发段，继而再重复上述过程。导热块将冷凝段释放的热量传给集管中的去离子水，去离子水在循环泵的驱动下进入去离子水循环子系统，实现能量的循环。隔热材料和保温盒起到保温的作用，减少热量的损失。

1.2 模型推导与简化

在集热器的集热过程中，被加热的热管、真空玻璃管不可避免地经由各种途径向周围散失一些热量。如果各种热量损失都考虑的话，过程比较复杂。为了更方便地研究热管式真空管集热器的热性能并简化计算，作如下假设：

l)忽略真空管内空气对流和传导热损失。

2)真空管总热损系数UL在一定温度范围内为常数。

3)忽略热管管壁、导热块和集管管壁的传导热阻。

4)忽略吸热板与热管蒸发段之间以及导热块与热管冷凝段、集管之间的接触热阻。

5)忽略玻璃管对太阳辐射的吸收。

6)热管内传热介质的蒸汽温度均匀一致。

基于以上假设，根据能量守恒基本定律，图1所示的太阳能集热系统中的采热子系统获得的太阳能Qall，一部分以热传导的形式散失到外部环境Qloss，一部分供给用热设备Qpre，剩余部分以热能的形式存储在储热水箱内Qw。可以描述为以下公式：

Qall=Qloss+Qw+Qpre

(1)

根据太阳能集热器的辐射传热机制，其辐射能表示为：

(2)

式中，AC为集热装置的采光面积，单位为m2；I为太阳辐照度，单位为W/m2；(τα)e为集热装置的有效透射率与吸热表面吸收率的乘积；FC[3]为太阳能集热系统的热转移因子，它是工质的有效热容与总热容之比，显示了系统把实际的热量转换成有效的热量的能力，其表达式为：

(3)

式中，Cw为系统有效工质的热容，Cm为系统无效工质和有直接热转移材料的等效热容，单位为J/(kg·K)。

系统的热量损失Qloss主要包含集热器的能量损失Qjrq和储热水箱的能量损失Qsx这2部分：

Qloss=Qjrq+Qsx

(4)

根据牛顿冷却公式，利用散热系数来计算散热量，集热器能量损失Qjrq和储热水箱的能量损失Qsx分别如公式(5)与公式(6)所示。

Qjrq=wAGULG(tmG1-tmG2)/FC

(5)

式中，tmG1为集热管内管外壁的平均温度，tmG2为集热管外管内壁的平均温度，单位为℃；ULG为集热管的散热系数；AG为全部真空集热管内管的面积和；w为真空集热管的有效散热面积系数。

Qsx=AXULX(tmX-ta)/FC

(6)

式中，AX为水箱的散热面积，ULX为水箱的散热系数，tmX为水箱壁面的平均温度，ta为环境温度。

将公式(5)和公式(6)代入公式(4)，系统总的热量损失可描述为：

Qloss=(wAGULG(tmG1-tmG2)+AXULX(tmX-ta))/FC

(7)

通过分析计算和测量验证，集热管内管外壁的平均温度tmG1、水箱壁面的平均温度tmX、集热管中工质的平均温度tmG和储热水箱工质的平均温度tm近似相等，集热管外管内壁的平均温度tmG2和环境温度ta近似相等。公式(7)可整理为：

(8)

水箱内存储的能量Qw可以表示为：

Qw=mCpΔtm

(9)

式中，m为水箱内水的质量，Cp为水的比热容，Δtm为单位时间内水箱内的水的温度变化。

将公式(2)、公式(8)和公式(9)代入公式(1)整理得：

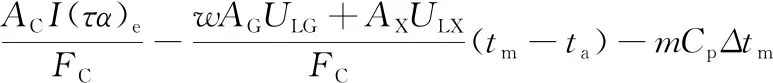
(10)

公式(10)中I、tm、ta、Δtm是变量，可以通过传感器实时测量获得；AC、AG、AX、(τα)e、FC、w、ULG、ULX、m、Cp是常量。令：

公式(10)经以上简化处理便可获得太阳能集热系统集热量混合模型的最终表达形式：

Qpre=aI-b(tm-ta)-cΔtm

(11)

式中，未知参数a、b、c为模型的待辨识参数。

2 模型的辨识方法

其中，n是测得数据的组数。

基于粒子群优化算法[17-19]具有鲁棒性好、易收敛等优点，本文选用通用的粒子群算法求解此优化问题。粒子群优化算法是一种模拟鸟群觅食过程的优化计算方法，通过群体速度、位置信息的共享和更新不断向优化目标靠近，在寻优过程中，粒子跟踪个体和群体的历史最优位置，达到最大设定的迭代次数T或者满足预定最小适应度阈值γ，就停止迭代，输出找到的最优结果。

典型PSO的演化方程可以描述为：

(13)

(14)

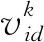
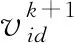
图3描述了典型PSO优化算法的求解过程，其详细的计算步骤如下：

Step1初始化种群的各类参数：c1、c2、每个粒子搜索空间的上限ud和下限ld、T、γ、粒子速度的最小值vmin和最大值vmax，随机初始化种群中每个粒子的位置和速度。

Step2根据适应度函数计算每个粒子的适应度值fitness，并把gbest、pbest和种群中所有粒子的最佳适应度值更新。

Step3根据公式(13)和公式(14)更新粒子的速度和位置。

Step4计算每个粒子的适应度值，将每个粒子的适应度值与其pbest比较，如果较好，则将其当前的位置作为该粒子的pbest；将每个粒子的pbest与gbest进行比较，如果更优，则更新gbest和最佳适应度值。

Step5判断搜索到的结果是否满足迭代停止条件，若满足停止条件则输出最优位置和最佳适应度值，否则转到Step3继续运行直到满足条件为止。

本文利用上述的PSO优化算法辨识公式(11)所描述的模型参数。将公式(11)代入公式(12)，该优化问题的目标函数可进一步描述为：

(15)

该目标函数中有a、b、c这3个未知参数，因此该优化问题的解空间维数为3。令Xi=(ai,bi,ci)表示第i个粒子的空间位置，Vi=(vi1,vi2,vi3)表示第i个粒子的速度。优化问题初始化参数[20-21]为：初始化M为150,ud为8,ld为-8,vmin为-1.2,vmax为1.2，惯性因子初始值ω=0.9，加速系数c1和c2都取为2。迭代中止条件选为最大迭代次数100和最小适应阈值取为0.005 kW。把辨识模型参数的仿真数据应用于图3所描述的PSO优化算法中，求解此优化问题所获得的最优解即为模型的最优参数。

3 仿真数据的获取与模型验证

3.1 仿真系统的搭建与仿真数据的获取

为了验证模型的有效性，本文采用TRNSYS仿真软件搭建太阳能集热系统仿真模型，通过仿真实验获取辨识模型的仿真数据。TRNSYS仿真软件是基于模块化的动态仿真程序，每个模块都可实现自身的一种特定功能，通过调用与系统相关的功能模块，根据各功能模块的输入输出关系，按照图1所示的太阳能集热系统结构图依次连接各功能模块搭建仿真系统[22-24]，如图4所示。该仿真系统采用的功能模块包括气象数据模块(Type 15-YMY)、热管式太阳能集热器(Type71)、储热罐模块(Type4b)、集热泵模块(Type3b)、温差控制器(Type2b)和在线绘图仪(Type65c)等。气象数据模块为太阳能集热器提供太阳辐照度、环境温度等气象参数。温差控制器根据集热器与水箱的温差以及用热设备所需温度与水箱温度的差值分别控制集热泵和侧源泵的运行，实现集热和供热的功能。在线绘图仪负责采集太阳能辐照度、环境温度、水箱温度等模型辨识所需的仿真数据，仿真数据边界条件如表1所示。至于仿真数据是否与实际结果相吻合，依赖于TRNSYS仿真软件建立这些功能模块所采用的模型。从TRNSYS仿真软件在全球的应用普及范围来看，该软件应该值得信任。仿真系统各模块的设计参数如表2所示。

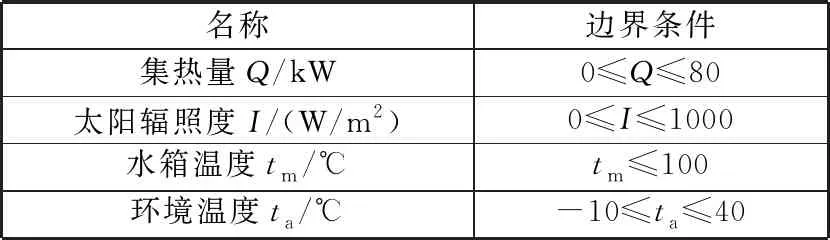
表1 输入输出变量的边界条件

表2 太阳能集热系统设计参数

为了使仿真系统获得的仿真数据更具有代表性，在气象数据模块中选择济南市2021年7月1日—7月31日的气象数据(如图5和图6所示)作为环境条件进行仿真实验。因夜间太阳能辐照度为0，采集不到太阳能，故选择每天的10:00—16:00对仿真数据进行采集。另外，为了确保采集的仿真数据覆盖各种工况条件，太阳辐照度、水箱温度以及环境温度等变量按表1给出的边界条件进行设定，让变量在边界条件范围内连续变化，每隔0.5 h对仿真数据进行一次采集，故7月份共获取仿真数据403组。最终随机选取100组数据作为训练样本，从剩余数据中再随机选取50组数据作为测试样本。

3.2 模型仿真验证与比较

使用仿真实验获取100组训练样本数据，利用前面所述的模型辨识方法，获得的模型参数值为：a=0.049,b=0.470,c=-6.392。

为了验证模型的有效性，采用公式(16)所描述的相对误差Re[25-26]对模型的预测精度进行评估。

(16)

为了验证模型在集热量预测方面的性能，分别使用训练数据和测试数据对模型的预测值与实际值进行比较，实际值是仿真数据中模型输出变量值。结果如图7和图8所示。比较结果表明，不管是使用训练数据还是使用测试数据，模型的预测结果都能与实际测量结果很好地吻合，其预测相对误差均在4%以内。为了进一步分析模型的预测精度， 图9和图10分别画出了使用训练数据和测试数据时模型的相对误差，从图中的数据可以看出相对误差均较小，模型的精度较高。经计算，使用训练数据和测试数据时模型的平均相对误差[27]分别为1.8%和2.02%，由此可以看出，使用训练数据辨识出模型参数，再用测试数据预测模型结果时，预测精度会有所下降，但下降幅度不大，在可接受的范围内。

为了进一步说明模型的有效性，选择已有文献中实用效果较好的经验模型和机理模型进行比较，模型误差对比如表3所示。

表3中的比较结果表明，纯机理建模方法所获得的机理模型对经验参数的依赖性较强，而经验参数很难适应各种环境条件，所以理论模型的误差较大；经验建模充分利用实验数据辨识模型参数，实验数据中包含了环境条件对模型参数的影响，故而模型误差较小；混合建模方法的模型结构来源于理论推导，其模型参数利用实验数据辨识获得，充分利用了2种建模方法的优点，因此其模型精度更高。文献[15]用神经网络和数学模型相结合的方法建立太阳能集热器神经网络模型，该方法适用于集热系统的优化设计，本文提出的建模方法主要面向系统的实时优化控制。文献[15]的模型用于预测集热系统的效率与集热器出口温度，其平均相对误差较小，可以达到1.2%；而本文建立的模型面向优化控制，用于预测集热系统的集热量，因集热量除了与集热器出口温度有关外，还与流量等因素有关，故其误差偏大，约为2.02%。虽然误差略微偏大，但仍能满足系统优化控制的需求。

4 结束语

本文充分利用机理建模与经验建模方法的优点，提出了热管式太阳能集热系统根据环境条件预测集热量的混合模型。通过简化，把理论模型中的经验参数和几何参数集总为待辨识的未知参数。利用TRNSYS仿真软件搭建太阳能集热系统模型，通过仿真获取模型辨识数据，借用粒子群优化算法代替模型辨识算法，对模型参数进行辨识。训练结果和测试结果表明，该模型能准确预测太阳能集热系统在各种工况下的集热量，平均相对误差在2%左右。与现有的模型比较的结果表明，该模型的预测精度得到了进一步的提升。本文提出的模型将在太阳能空调、太阳能热泵、太阳能采暖等系统的优化运行调度中得到广泛应用，而且在太阳能集热系统性能评估和故障检测诊断中也具有广泛的应用前景。