基于局部投影的视差图像拼接平滑优化
刘 杰,游品鸿,田 明,刘金凤
(1. 哈尔滨理工大学测控技术与通信工程学院,黑龙江哈尔滨 150080;2. 中国电信黑龙江省分公司,黑龙江哈尔滨 150080)
1 引言
图像拼接是将多幅图像的重合部分合并成具有较宽视野的大场景图像的过程. 它被广泛地应用在无人机[1,2]、图像遥感[3]、3D 重建[4]和VR[5]图像等重要的领域,因此以高效的方式生成高质量的拼接图像是至关重要的.
传统的拼接算法是基于尺度不变特征(Scale In⁃variable Feature Transform,SIFT)[6]对图像进行全局变换的. Brown 等人[7]提出的AutoStitch 基于SIFT 算法进行图像的特征点提取,通过两幅图像之间的单应性矩阵对图像进行对齐,但该方法对具有视差的图像会出现伪影的情况. 为了获得更高的拼接质量,全局变换已不能满足环境比较复杂的场合的需求. 徐弘祯等人[8]通过RANSAC(RANdom SAmple Consensus)与LM(Levenberg-Marquardt)算法相结合的方式进行误匹配点的剔除,提高了图像拼接的质量,缺点是不能多角度地获取图像数据和局部误匹配异常值的去除,因此该算法受到的约束较多.Zaragoza 等人[9]提出的逼近投影变换(As-Projective-As-Possible warp,APAP)在重合区域使用局部投影变形的同时,引入了局部线性变换方法消除图像之间的不正确数据匹配,提高重合部分匹配的准确率,但是APAP 算法采用局部投影结合全局投影进行对齐,这样的结果会导致非重合区域的变形,即拼接图像的一部分会出现不均匀的拉伸. 赵春晖等人[10]采用归一化互相关函数在网格的框架下对匹配点位置进行约束求解,其结果提高了匹配的准确率,但没有考虑非重合区域可能出现的失真或扭曲的情况.
针对上述问题导致图像拼接出现局部的图像扭曲的现象,本文提出了一种基于局部投影的视差图像拼接的平滑优化算法. 该算法通过局部保留结构对提取的特征点进行匹配,将匹配的特征点进行投影矩阵计算和图像拼接,对重合区域计算最优投影矩阵,利用符合要求的投影矩阵进行图像拼接,在对齐拼接完成后,通过变形函数计算非重合区域的变形程度,对失真图像进行平滑过渡,从而提高图像的质量.
2 算法说明
2.1 算法结构框图
本文算法的框架如图1 所示. 图像拼接的第一步是将获取的图像分为参考图像和待拼接的图像,通过SIFT 算法对获取的图像进行特征点检测;第二步是将获取的特征点通过图像配准进行特征点匹配,利用配准之后的匹配点进行投影矩阵的计算;第三步是根据第二步的投影矩阵进行最优投影矩阵的计算,通过归一化距离的计算结果与设定的阈值进行大小判定,当计算结果小于设定的阈值时,投影矩阵保留并进行图像拼接,否则,选取其他投影矩阵重新进行阈值的判定;第四步是在拼接完成后,通过变形函数计算非重合区域的扭曲程度,采用平滑的方式对局部的图像扭曲进行平滑过渡.

图1 算法流程图
2.2 图像配准
本文基于局部保留结构方法对图像进行特征点匹配,通过成本函数对特征点的距离进行成本计算,对给定的两幅图像的特征点,取S={(xi,yi)},i∊{1,2,…,n}为一组作为n个特征对应关系集合[11]. 其误匹配点滤除的点集解为
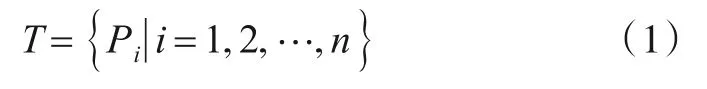
其中,设定Pi∊{0,1},匹配对是否匹配正确由Pi表示,当Pi=1时表示第i个对应项为匹配正确项,当Pi=0时表示第i个对应项为匹配错误项. 对成本函数进行计算,其具体满足如下条件:


其中,d是距离度量;Nx表示对应的特征点x在欧几里得距离下的领域,在相应的领域中,每个特征点搜索4个领点;将p定义为集合S与n×1 个二元向量关联;ci是成本函数中衡量第i个匹配项(xi,yi)是否满足局部保留结构的几何约束成本,正确的匹配会带来零约束成本或少量约束成本,而错误的匹配会增加约束成本.Pi的取值与ci和λ之间的比值有关,而λ是用来衡量图像变形的加权参数,本文将入设为0.9,即

2.3 图像投影
通过2.1节的方法对图像进行配准和图像拼接,其结果不管是在主观感受还是客观的质量评价上都不理想. 因此,为了进一步提高图像拼接的匹配精度,本文在第一次投影拼接的基础上,对拼接之后的图像进行再次投影矩阵计算,选取最优投影矩阵进行二次投影.首先,将局部保留算法得到的匹配点进行投影矩阵的计算并投影拼接;然后图像拼接完成后,通过重合区域边界点与投影矩阵之间的关系进行最优矩阵的寻找.具体公式如下:


图2 所示为RANSAC 算法与本文算法进行匹配点剔除比较. 图2(a)为RANSAC 算法剔除的结果,由图可知红色的线条为局部异常值没有剔除掉的结果;图2(b)为本文算进行匹配点剔除的结果,由图可知没有出现局部异常值;图2(c)为采用RANSAC 进行误匹配点剔除后拼接的结果,其结果出现明显的重影;图2(d)为本文算法进行图像拼接的结果,其结果无明显的重影.

图2 图像拼接对比
2.4 局部投影的平滑过渡
采用全局变换对视差图像进行拼接,优点是图像在非重合区域不会出现局部扭曲的问题,其缺点是拼接结果在重合区域会出现对齐不准的现象;采用弹性翘曲模型对图像进行拼接,其结果在重合区域能有效提高对齐精度,但不足是在非重合区域拼接结果会出现局部的图像扭曲. 因此,为了提高图像拼接的质量,利用全局投影和局部投影的点坐标进行偏差计算,将结果进行平滑优化. 本文采用径向基函数(Radial Ba⁃sis Function,RBF)[12,13]的薄板样条(Thin-Plate Spline,TPS)[14~16]计算图像的变形函数,变形函数的扭曲模型如图3 所示,其中g(x,y)与h(x,y)分别为x和y方向上发生的变形.

图3 变形函数

由于全局投影矩阵对目标图像的非重合区域具有良好的保留效果,不会导致局部的投影扭曲,因此为了消除局部投影带来的负面影响,计算wi的权重将局部投影平滑过渡到全局图像. 假设在x与y的方向上重合部分的边界为[xl,xh]与[yl,yh],在非重合部分出现的局部变形时,权重wi的具体表达形式如下:

在这里K是一个比例参数. 将上述各个函数代入得到的结果进行图像的平滑优化,成像结果能够很好地保留非重合区域的整体投影.
3 实验与结果分析
本文对多个场景进行图像拼接算法验证,实验平台采用的CPU 型号为Inter i7 处理器,内存为8G,操作系统为Windows7.
3.1 主观评价
在主观评价中,本文通过视差图像进行实验结果说明. 如图4所示,图中标号1的白色灯杆为重合区域,图中标号2 的摄像头栏杆为非重合区域. 图4(a)采用全局投影进行图像的拼接,其优点是能够较好地保留拼接之后图像的整体性,使得拼接图像看起来更加自然;但缺点是如果图像拍摄的角度不在同一平面,采用全局投影就不能准确地对齐重合部分,如图4(a)中的标号1 所示,白色灯杆由于视差原因造成图像出现重影. 图4(b)采用APAP 算法进行局部投影,可以看到白色灯杆的重影与全局投影相比,其结果有所改善,但还是有一小部分重影,同时摄像头的栏杆出现局部的扭曲,如图4(b)中的标号2 所示. 图4(c)采用本文算法进行局部投影,在重合部分,两幅图像匹配点基本对齐,没有出现重影的问题;在非重合部分,摄像头栏杆部分的扭曲有着明显的优化,使得整体看起来更加自然.

图4 算法比对结果图
采用文献[7]算法、APAP 算法和AANAP 算法[17]与本文算法对输入的图像数据进行拼接实验,通过以下几组数据对这些算法进行实验对比,其结果如图5所示.
在图5(a)中,输入图像是以上下倾斜的视差角度进行拍摄. 采用文献[7]算法对图像进行拼接:由于使用全局投影进行图像拼接,非重合区域图像的整体性有良好的表现,其结果如文献[7]算法中的标号2所示;但是在重合区域,树木和路面地砖的纹路均出现了不同程度的重影,其结果如文献[7]算法中的标号1 和3所示. 采用APAP 对图像进行拼接:在重合区域,由于使用了局部投影进行图像的对齐,拼接之后没有出现重影,其结果如APAP 算法中的标号1和3所示;但是由于采用了局部投影,像素点的对齐导致非重合区域的图形发生扭曲,其结果如APAP 中的标号2 所示. 采用AANAP 算法对图像进行拼接:重合部分的拼接结果表现良好,无重影现象;在非重合区域,如AANAP 中的标号2 所示,路面出现扭曲的现象. 采用本文算法对图像进行拼接:在重合区域,图像拼接结果无重影现象,实验结果如本文算法中的标号1 和3 所示;在非重合区域,通过变形函数将图像扭曲的部分平滑过渡到全局变换,其结果如本文算法中的标号2 所示,拼接的图像整体性更好.
在图5(b)中,输入图像是以同一水平面不同视差角度进行拍摄,该图像数据的重合部分占90%以上. 采用文献[7]算法:如标号1 和2 所示,由于采用了全局投影变换对齐图像,重合部分的图像出现局部的重影和错位的问题. 采用APAP 算法:如像标号1所示,在重合部分,虽然优化了图像的重影,但是出现了和标号2 一样的错位结果. 采用AANAP 算法:由于采用了局部的自适应变换,该算法提高了图像的对齐精度,其结果如标号2 所示,但还是会出现如标号1 的错位问题. 采用本文算法:通过本文算法进行图像的拼接,提高了图像对齐的精度,解决了两幅图像拼接错位的问题,其结果如标号1和2所示.
实验结果表明,对于重合部分大于90%以上的源图像,拼接算法造成非重合区域的扭曲现象不是很明显,其结果如图5(b)中各个算法的标号3所示.

图5 图像结果比对
3.2 客观评价
为了更加客观地对拼接之后的图像质量进行评估,本文采用结构相似性(Structural Similarity Index,SSIM)[18]对多组图像结果进行客观评价,其评价指标SSIM 的值越大,说明图像拼接之后的结果与目标图像越相似. 其中图像数据库包括文献[9]以及本文自行拍摄采集的数据,表1 为对图像数据进行SSIM 的客观评价结果. 关于SSIM 目标源的选取,本文通过相机拍摄目标物体的重合部分,将拍摄的重合图像与拼接结果的重合部分进行SSIM的算法比较.
本文对客观的SSIM图像数据评价结果和上述的主观评价结果进行了分析. 从表1 可以看出,有6 组的数据在4种图像拼接算法的得分呈逐级递增,其中第五组数据中,由于图像重合部分超过90%及拍摄的视差角度相对较小,因此AANAP 算法与本文算法得分相近.综上所述,本文算法的总得分要高于其他算法. 因此,本文算法的拼接结果要优于其他算法,本文算法能够有效地将图像进行对齐以及优化图像的局部扭曲,提高图像拼接的质量,有效地满足实际工程实践的应用需求.
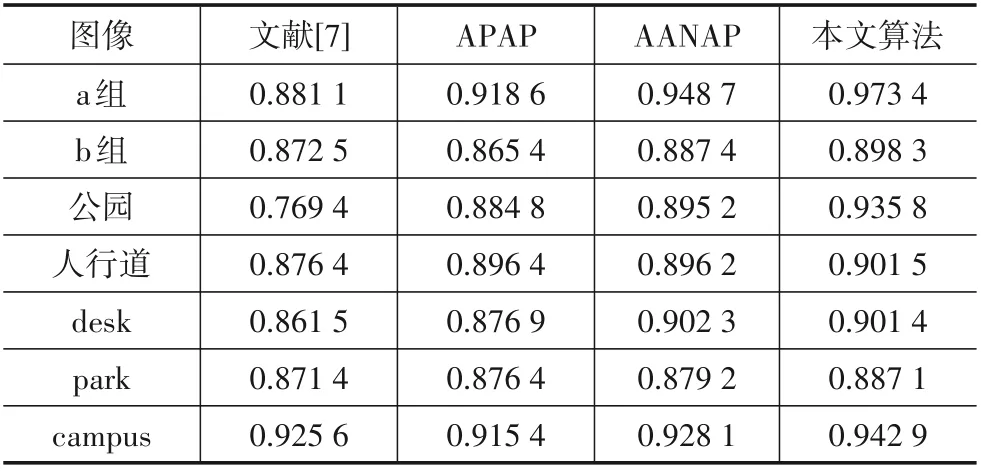
表1 SSIM的图像数据评价
4 结论
针对图像拼接的局部投影存在对齐不准及非重合区域存在失真和扭曲的问题,本文提出了一种基于局部投影的视差图像拼接的平滑优化算法,并从主观评价和客观评价2 个方面验证该算法. 在主观评价中:本文算法通过SIFT 进行特征提取,由局部保留结构对图像进行特征点匹配,通过投影矩阵进行阈值判定,将符合条件的矩阵进行图像拼接;在非重合部分,结合TPS对图像进行变形函数模型的建立,通过平滑优化非重合区域,逐渐将局部投影造成的图像变形进行平滑过渡,所得结果不仅提高了图像的对齐率,还避免了图像的局部失真和扭曲问题. 在客观评价中:通过SSIM 评价指标对文献[7]算法、APAP 算法、AANAP 算法和本文算法进行评价对比,结果显示本文算法的评价结果要优于其他3种算法.

