基于特征区域划分的文物碎片自动匹配算法
赵夫群,耿国华
(1. 西安财经大学信息学院,陕西西安 710100;2. 西北大学信息科学与技术学院,陕西西安 710127)
1 引言
随着3D 扫描技术的日趋成熟,得到文物的精确的三维模型坐标已经非常容易,而如何将破损文物进行修复和展示则逐渐成为3D 建模的关键. 传统的文物修复主要采用手工方式实现,不仅修复速度慢、准确率低、可逆性差,而且容易造成二次破坏、数字化展示困难等问题[1,2]. 因此,利用计算机技术可以高速、便捷、无破坏地实现文物虚拟复原,提高文物修复的效率和准确率,并以虚拟复原指导文物实体复原,对文物数字化保护和展示有着至关重要的意义.
碎片匹配是文物虚拟复原的重要研究内容之一,通过碎片匹配可以将文物碎片进行对齐拼接,为后续的碎片融合和虚拟展示提供技术支持. 碎片匹配算法主要分为两大类:一类是无特征的碎片匹配,另一类是基于特征的碎片匹配. 其中,基于特征的碎片匹配算法的应用更为广泛,如点特征、线特征、法线和曲率特征等. Ouyang 等[3]利用特征点实现碎片匹配,但效率较低、稳定性较差;Patel[4]提出基于改进SURF 的匹配算法,可以提高匹配速度,但对低重叠点云的匹配误差较大;周光兵等[5]提利用图像灰度值实现3D 刚性匹配,可以获得较高的匹配精度;廖梦怡等[6]利用投影角点检测算法实现点云匹配,可以有效提高匹配精度;陈宝华等[7]提出一种稠密三维点云与图像的匹配算法,实现了不同视场图形的匹配问题;任明荣等[8]提出一种三维模型匹配的条件随机场算法,有效提高了匹配精度;Xu 等[9]提出基于几何特征向量的点云匹配算法,可以降低耗时,提高鲁棒性和可靠性;Shi 等[10]提出一种基于轮廓特征的点云匹配算法,但是该算法对轮廓特征破损严重碎片模型的匹配效果不佳;Wu等[11]提出一种基于距离误差评价高密度点云匹配算法,但是对低重叠率点云的匹配精度不高;Yan等[12]提出一种基于遗传算法(Genetic Algorithm,GA)的点云匹配算法,可以避免陷入局部最优解,但同样不适用于低重叠点云匹配.
以上基于特征的匹配算法均存在一定的问题,如:匹配精度低,收敛速度慢;约束条件过于严格,容易造成局部最佳匹配;花费大量时间在无用的匹配上;重叠比例较低点云的匹配效果不佳. 鉴于此,针对文物的点云模型,本文提出一种基于特征区域划分的匹配算法,通过获取点云特征点并对特征点集进行区域划分以降低匹配规模,同时提高点云区域的重叠率,从而达到点云快速精确匹配的目的,提高低重叠断裂面文物的匹配精度.
2 特征点提取
对于待匹配的文物碎片,首先采用基于法矢的断裂面分割算法[13]提取其断裂面,然后提取断裂面上的特征点并对其进行区域划分,由此提高低重叠断裂面的匹配精度和速度.
假设某一断裂面φ1对应的点云模型为P,对于其上任意一点p,以圆心为p、半径为r的球型区域内的点来构建协方差矩阵C,并求解该协方差矩阵C的特征向量和特征值,其中最小特征值对应的特征向量就是点p的法向量.
构建点p及其邻域内点的协方差矩阵C为
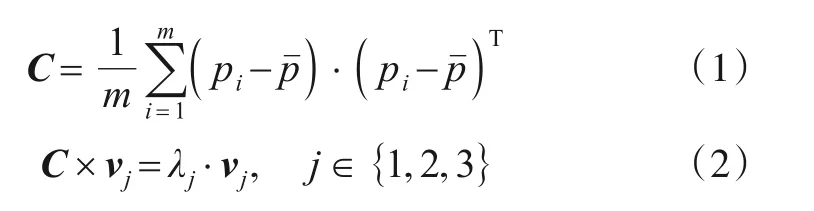
式(1)、式(2)中,m表示以p为圆心、r为半径的邻域内点的数量;pˉ表示该邻域的质心;pi是p邻域内的点;λj表示协方差矩阵C的特征值;vj表示特征值λj对应的特征向量. 当特征值最小时,将其所对应的特征向量作为点p在该邻域下的法向量n.
假设点p在半径r1和r2(r1≠r2)邻域下的法向量分别为n1和n2. 由于在不同的半径下邻域曲面的变化程度不同,因此两个方向量n1和n2之间必然存在角度偏差,且角度偏差越大,表示曲面变化越剧烈. 通过计算两个法向量n1和n2间夹角余弦来设定阈值ε1,以提取特征点,即

式(3)中,阈值ε1的值要根据具体实验情况来确定.对于点云P如果其外表面法向量变化较大,则需要提取的特征点较多,那么ε1的值要设置得大一些,否则设置得小一些,但ε1的值不能大于符合式(3)的最大值.
对于两个待匹配的断裂面φ1和φ2,假设其对应的点云模型分别为P和Q,利用上述特征点提取方法对其进行特征点提取,得到的特征点集分别为P'和Q'. 接下来对特征点集P'和Q'进行区域划分,为后续区域匹配提供数据基础.
3 基于区域划分的初始匹配
3.1 特征点区域划分

3.2 区域匹配


式(4)中,L=MN;ωi表示线性组合系数,i=1,2,…,L.
在理想情况下,ωi的非零元素集合所对应的区域匹配程度会比较高,所对应的刚体变换与真实刚体变换是最接近的. 线性组合系数ωi通过最大化能量函数E(ω)来计算,计算式为

式(6)中,参数σ是一个大于0 的实数,用来控制可信性和一致性信息的相对重要程度.
参数σ的值越大,一致性信息所起的作用就越大.当两个待匹配断裂面的重叠区域较小并且重叠区域内的特征比较明显时,需要依靠该特征区域来恢复全局变换,σ的取值应该较小;反之,σ的取值应该较大. 在实际实验中,配准结果对σ的取值默认设置为1.0 即可.d(Ti,Tj)表示刚体变换Ti和Tj的距离,采用标准化的欧氏距离计算,即

由于矩阵A是对称的,因此它的最大特征值所对应的特征向量是ω,最大化能量函数为E(ω). 根据Perron-Frobenius 定理[16],ω的所有分量具有相同的符号,因此可以选择合适的ω使得它的各个分量都是正数,那么该ω就是需要求解的最优组合系数.
刚体变换T可分解为一个3×3 旋转矩阵R和一个3×1 平移向量t. 对于平移向量t,直接平移计算即可.而对于旋转矩阵R,采用四元数法[17]来计算,即
通过计算旋转矩阵R和平移向量t即可求得刚体变换T,实现特征点集P'和Q'的初始配准. 最后,采用一种基于阈值约束的改进ICP算法实现点云精确配准.
4 基于阈值约束ICP的精确匹配
ICP 算法通过不断迭代来求解两组点云之间的刚体变换,每次迭代都会求解点云变换矩阵,使得通过该矩阵变换得到的点云与目标点云对之间空间距离最小[18]. 该算法具有较高的匹配精度,但耗时较长,且要求待匹配点云存在包含关系. 鉴于此,在碎片断裂面精匹配阶段,本文采用一种基于阈值约束的ICP算法[19]将特征点集P'和Q'进行进一步匹配.
采用该基于阈值约束的ICP 算法对P'和Q'精确匹配的具体步骤如下.
(1)设置初值:旋转矩阵R'0,平移矢量t'0,迭代次数k=1.
(2)计算目标函数Fk,计算式为

通过以上对特征点集P'和Q'的精确匹配,即可达到文物碎片断裂面最终精确匹配拼接的目的.
5 匹配算法步骤描述
基于以上断裂面初始匹配和精确匹配方法,该基于特征区域划分的文物碎片匹配算法的具体步骤描述如下.
(1)假设两个待匹配的文物碎片为B1和B2,提取的其断裂面集合分别为F1={S11,S12,…,S1n}和F2={S21,S22,…,S2m},n和m分别表示碎片B1和B2所含断裂面的数目.
(2)在断裂面集合F1和F2中,任取两个未匹配过的断裂面S1i和S2j,i=1,2,…,n,j=1,2,…,m,提取断裂面S1i和S2j上的特征点,得到特征点集特征点集P'和Q'.
(3)对特征点集P'和Q'进行区域划分和区域匹配,从而将断裂面S1i和S2j初步对齐.
(4)采用该基于阈值约束的ICP 算法对特征点集P'和Q'进行进一步精确匹配,从而实现断裂面S1i和S2j的进一步对齐.
(5)判断断裂面S1i和S2j的匹配误差,若小于给定阈值,S1i和S2j匹配成功,否则从断裂面集合F1和F2中取下一对未匹配过的断裂面S1i和S2j,重复步骤(2)到步骤(5),直到找到可以成功匹配的两个断裂面或所有断裂面匹配完为止.
6 实验结果与分析
算法在Visual studio 2010 环境下,Intel Core i7 3.33GHz 的CPU、16GB 内存的Windows 7 64 位PC 机上进行实现. 实验数据是采用加拿大手持式Handyscan3 D激光扫描仪获取的兵马俑碎片的obj格式的点云数据模型.
6.1 两个碎片的匹配
四组待匹配的兵马俑碎片如图1 所示. 首先,提取碎片断裂面上的特征点,并对其进行区域划分;然后采用4PCS 算法进行区域匹配,从而实现两个碎片断裂面的初始匹配;最后采用基于阈值约束的ICP算法将特征点集进行精确匹配,从而将断裂面进行最终匹配. 碎片初始匹配和精确匹配结果分别如图2和图3所示.

图1 待匹配的兵马俑碎片
从图2 和图3 匹配结果可见,该基于特征区域划分的碎片匹配算法通过提取特征点并将特征点集进行区域划分和匹配,实现文物碎片的初始对齐,再利用基于阈值约束的ICP算法实现碎片断裂面的最终精确匹配.为了进一步验证该基于特征区域划分的碎片匹配算法的性能,对于图1 的四组文物碎片,再分别采用ICP 算法[15]、文献[10]算法、文献[11]算法和文献[12]算法对其断裂面进行匹配,匹配结果如表1所示.

图2 兵马俑碎片的初始匹配结果

图3 兵马俑碎片的最终匹配结果
从表1可见,该基于特征区域划分的匹配算法具有最高的匹配精度、最快的匹配速度. 与ICP 算法、文献[10]算法、文献[11]算法和文献[12]算法相比,该基于特征区域划分的匹配算法的匹配精度分别提高了约45%,35%,33%,22%,耗时分别降低了约26%,20%,16%,12%.

表1 五种算法的匹配结果
这是由于:ICP 算法对碎片的相对初始位置要求较高,且要求两个待匹配的碎片断裂面间存在包含关系,因此匹配精度和速度较差,其时间复杂度为O(MN),M和N分别表示两个待匹配点集的点数;文献[10]算法是一种基于X 射线层析成像数据的点云匹配算法,并将其用于跟踪原始沙粒中破碎碎片,但是该算法利用轮廓特征进行匹配,对轮廓特征破损严重碎片模型的匹配效果不佳,其时间复杂度为O(NlogM);文献[11]是一种基于距离误差评价的ICP 算法,可以实现高密度点云的有效匹配,但是对低重叠率断裂面的点云模型的匹配并无明显优势,其时间复杂度为O(NlogM);文献[12]算法是一种结合GA 和ICP 的点云匹配算法,利用最大归一化匹配分数配准模型实现匹配,可以克服ICP 算法依赖初始解和GA 容易陷入局部最优解的缺点,但是该算法不能提高低重叠断裂面的局部重叠率,因此对重叠率较低碎片断裂面的匹配效果不佳,其时间复杂度为O(max(M,N));而本文提出的基于特征区域划分的匹配算法不仅通过提取特征点大大降低了匹配的规模,而且通过区域划分大大提高了区域点云的重叠率,并通过在ICP算法中加入阈值约束提高了低重叠点云的匹配精度和速度,其时间复杂度为O(log(max(M,N))). 由此可见,该基于特征区域划分的匹配算法是一种快速精确的文物碎片匹配算法,尤其对低重叠断裂面的碎片具有良好的匹配结果.
6.2 多个碎片的整体拼合
基于本文提出的两个碎片断裂面的匹配算法,接下来采用子图融合法[10]实现多个兵马俑碎片的整体拼合. 首先采用基于特征区域划分的碎片匹配算法将碎片进行两两匹配,确定碎片间的匹配关系,并根据该匹配关系确定所有碎片的匹配关系图;然后将满足匹配条件的碎片进行融合,直至所有的碎片融合为一个整体为止. 在融合的过程中允许回溯,即对于碎片融合过程中出现的无法融合的碎片可以进行重新融合.
以G10-52 号兵马俑的拼合为例,该兵马俑含碎片68个,部分碎片如图4所示. 该68个碎片可拼合成一个俑,不存在孤立的碎片. 通常一个碎片的断裂面不止一个,因此一个碎片可能对应多个不同的匹配碎片,从而使得碎片间存在一对多的匹配关系.G10-50 号俑的所有碎片的整体拼合结果如图5 所示. 由图5 可见,本文提出的碎片匹配算法可以实现兵马俑碎片断裂面的有效匹配.

图4 部分待拼合兵马俑碎片

图5 碎片整体拼合结果
7 结论
在文物碎片自动匹配拼接过程中,针对传统基于几何特征匹配算法不能有效解决断裂面重叠比例较碎片的匹配问题,本文提出了一种基于特征区域划分的碎片断裂面匹配算法. 首先,通过构造特征点局部区域的法线向量特征,获得断裂面的特征点及特征点集;然后,将提取的特征点集划分为多个区域,并进行区域匹配以实现碎片初步匹配;最后,采用基于阈值约束的ICP 算法实现断裂面的进一步的精确匹配,从而达到文物碎片匹配拼接的目的. 该算法不仅可以大大减少匹配的数据规模,而且可以有效改善特征区域的重叠范围,其匹配的时间效率和匹配精度比许多传统算法至少可以分别提高10%和20%. 但是,算法中没有考虑大量噪声对碎片匹配结果的影响,使用的数据模型都是低噪声的文物碎片点云数据模型. 因此,在今后要继续研究更加通用的文物碎片匹配算法,着重加强噪声和点密度对匹配结果的影响,提高文物虚拟复原的正确率.

