利用改进的f-k滤波方法压制探地雷达中的线性干扰
张力文,聂俊丽
(贵州大学国土资源部喀斯特环境与地质灾害重点实验室,贵州贵阳 550025)
1 引言
探地雷达(Ground Penetrating Radar,GPR)以其快速无损、探测精度高等特点,被广泛用于工程检测[1,2]、环境保护[3,4]、文物考古[5~7]、地质灾害[8,9]、反恐安检[10,11]、水文水利[12]等领域,是浅表地球物理探测技术中重要的手段. 在探测过程中,探地雷达会不断接收到周围物体界面反射的电磁波信号,这些信号不仅包括天线下方的反射信号,还包括天线四周的反射信号,四周的反射信号会对雷达解释造成一定的干扰,尤其是由墙体、倾斜地层等面状界面产生的空间干扰,这些干扰在雷达剖面表现为具有一定倾向的线性干扰,其能量强、范围广. 因此,压制这种线性干扰对探地雷达数据的解释至关重要.
针对数据中的线性信号,地震数据处理中常采用f-k变换进行处理.f-k变换实质上是一种二维傅里叶变换,主要是利用时间-空间域和频率-波数域2 个域之间的关系[13]. 如提取频散曲线等面波分析方法依据面波在f-k域上振幅能量最大的特点,在对应的f-v域中提取与频率对应的相速度值,从而得到面波记录中的频散曲线[14,15];波场分离方法依据有效波与干扰波的视速度差异,利用f-k变换分离不同波组[16,17]. VSP 数据处理中,Treitel 等采用f-k扇形滤波器,保留滤波范围内的信号,区分上行信号和下行信号[18],但存在混波、振幅畸变等缺陷[19~21]. 对此,朱海龙等人[22]提出了一种高保真的VSP波场分离方法以降低混波、振幅畸变,但需要对实际采集的数据进行偏移、坐标旋转等偏振滤波处理得到虚拟的上行波射线坐标,将复杂波场转换成简单波场. 此外,由于f-k变换方法属于多道处理的范畴,其处理结果受空间采样点的分布、深度采样间隔等采集参数的影响,使得f-k变换方法在使用中有着很大的限制[23].
鉴于探地雷达的原理和地震勘探相似,且电磁波类似于弹性波,因此一些学者尝试将f-k滤波方法应用于探地雷达数据处理中.Hayashi等人[24]利用f-k滤波压制数据中的直达波;余海忠等人[25]利用f-k滤波压制地面干扰波;翟波等人[26]介绍了f-k滤波的方法原理与常用的f-k滤波器. 在实际探测中,探地雷达仍有别于地震勘探,如地震勘探采集方式一般为一发多收的多偏移距方式,探地雷达则采用自发自收的共偏移距方式.采集方式的不同使得探地雷达剖面与地震剖面存在差异,且不具有时-空变特性,因而f-k变换方法在探地雷达中的使用限制小. 但采用常规f-k滤波方法压制线性干扰时,仍会存在滤波效果不理想的问题.
为此,本文提出了一种改进的f-k滤波方法压制探地雷达中的线性干扰. 本文将通过对模拟数据与实测数据中不同类型的线性干扰在f-k域的分布及频谱特征进行分析,针对不同区域内线性干扰的频谱特征分别设计特定的滤波范围进行滤波,达到压制数据中线性干扰的目的,并与常规f-k滤波方法进行比较,为工程应用提供一定的参考.
2 基本方法原理
2.1 常规的f-k滤波方法
仪器采集的数据是时间和空间的二维函数d(t,x),通过二维正、反傅里叶变换可得到其频率-波数(f-k)域频谱信息和时-空(t-x)域记录为

其中,f表示频率;k表示波数;D(f,k)为d(t,x)的频率-波数谱. 式(1)表明d(t,x)是由不同频率和波数的平面简谐波组成,频率和波数的关系为

其中,由于仪器总是沿测线进行探测的,故v为波的视速度. 而在f-k域图像中,纵坐标代表频率f,横坐标代表波数k,斜率代表视速度v,故具有一定视速度的波组在f-k域频谱特征的表现呈一条谱值射线,并且视速度越大的波组其谱斜率越大. 因此根据波组的视速度设计的合适滤波器进行处理可达到压制干扰波的目的.
f-k滤波器的性质由时间-空间特性h(t,x)或频率-波数特性H(f,k)所确定. 设y(t,x)为d(t,x)的f-k滤波输出结果,时间域中f-k滤波结果由输入信号d(t,x)与滤波因子h(t,x)的二维褶积运算实现;频率域中则由输入信号的频率-波数谱D(f,k)与滤波器的频率-波数特性H(f,k)相乘完成,即

其中,Y(f,k)和H(f,k)是y(t,x)和h(t,x)的傅里叶变换结果.
由于仪器采集的数据是时间序列长度有限的N道离散记录,故离散化后的f-k滤波公式为

其中,n为原始道号;m为结果道号. 由式(4)可知,测线上任一点处,f-k滤波的结果可由N道探地雷达数据道通过一维滤波结果相加而得. 可见,f-k滤波本身也是一种空间域的二维滤波.
在地震勘探数据处理中,利用实信号傅里叶变换结果具有对称性的性质,即负波数信号是正波数信号的复共轭,f-k滤波方法只对采集数据的f-k域正波数信号进行处理后,再通过对称性即可得到处理后的全频域信号.
2.2 改进的f-k滤波方法
实际探测中,探地雷达常用采集方式为自发自收的共偏移距方式,其偏移距可视为零,则反射时距曲线关系式为

其中,V为波速;H是天线到面状界面的垂直距离. 采集过程中,随着天线的移动,H会发生呈正或负的线性变化,其反射时间V也随之呈正或负的线性变化. 因此,探地雷达剖面中会出现倾向不同、视速度方向不同的2种线性干扰(见图1),其中向下倾的线性干扰(下行干扰)具有正视速度,向上倾的线性干扰(上行干扰)具有负视速度,其视速度v为
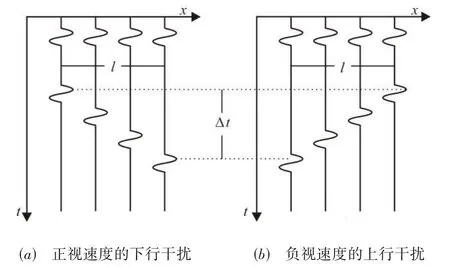
图1 探地雷达剖面中的倾斜线性干扰

其中,l为天线移动距离;Δt为相同波组的反射时间变量. 联合式(2)可知,探地雷达剖面中具有正、负视速度方向的线性干扰经f-k变换后,会位于f-k域的不同区域中,且根据其视速度的不同,所代表的f-k域频谱特征也不同.
常规的f-k滤波方法在处理过程中未考虑到探地雷达实际数据中线性干扰具有正、负视速度,且视速度值不同,导致其在f-k域分布及频谱上具有差异,在滤波时仅限于处理正波数域内的信号,因而对线性干扰的压制效果不理想.
为此,本文对f-k滤波方法进行改进,在滤波过程中对f-k域进行全域分析,对实际数据在f-k域中正、负波数域内的信号均进行处理,而不仅限于分析处理正波数信号. 具体方法步骤如下:
(1)采集探地雷达数据经过傅里叶变换后,得到其f-k域频谱;
(2)对f-k域全频域内的频谱特征进行分析,根据正、负速度线性干扰的f-k频谱特征及分布的差异,在正、负波数域内分别设计不同滤波区域,框选正、负波数域内线性干扰所在的区域;
(3)将选定的滤波区域内谱值置零,得到处理后的f-k谱;
(4)将处理后的f-k谱通过二维傅里叶反变换转换到时空域输出显示.
3 数值模拟及f-k滤波结果对比
本研究建立了如图2所示的数值模型,模型大小为1.4 m×1.1 m,网格大小为0.002 m×0.002 m×0.002 m. 模型分为两层介质:上面是1.4 m×0.1 m的空气层,相对介电常数为1;下面是粘土层,范围1.4 m×1.0 m,相对介电常数为9. 在粘土层中部有一埋深为0.66 m、半径为0.04 m 的圆形空洞,其中心位置为(0.7 m,0.3 m). 模型两端对称放置了两块0.2 m×1.0 m三角金属物体,倾斜面角度约为78.7°. 雷达天线的激励源采用点电偶极子源,激励波形为Ricker子波,频率为800 MHz,收发天线相距0.1 m,天线的移动步长为0.002 m. 为反映侧面物体在探地雷达剖面中产生的干扰情况,将测线的起点布置于左侧金属物体右侧(如图2所示),与左侧金属物底端相距0.02 m,测线终点布置于右侧金属物体左侧,如图2所示,与右侧金属物底端同样相距0.02 m,共采集430道数据. 模型中雷达测线的正下方只存在圆形空洞这一异常体.
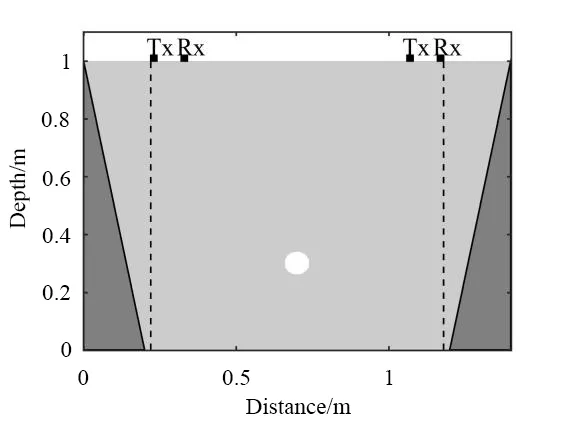
图2 数值模型
将模型的各参数编写入“.in”文件中,采用GprMax3.0软件进行数值模拟计算,得到如图3(a)所示的探地雷达剖面图. 在图3(a)中,双曲线信号为圆形空洞在雷达剖面产生的有效信号,与之相交的上、下行干扰则是由两侧金属物体产生的空间干扰波. 其中,下行干扰由左侧金属物体产生,上行干扰由右侧金属物体产生,且两者视速度值大小相等,约为0.05 m/ns;双曲线信号则不具有固定的视速度,其视速度随曲线切线改变而改变,但总体上视速度值均大于上、下行干扰的视速度值.
图3(b)是对数值模拟数据进行f-k变换后得到的f-k域频谱特征图,明显可见正、负波数域内频谱特征一致. 在图3(b)中,上、下行干扰在f-k域中均表现为以坐标原点为起点的谱值射线,其中下行干扰的f-k频谱特征位于正波数域内,上位行干扰的f-k频谱特征则于负波数域内,两者关于f轴对称. 同时,根据上、下行干扰的频谱射线得到两者的视速度值均在0.05 m/ns 左右,这与雷达剖面的视速度值基本一致. 而双曲线信号由于视速度不定,且视速度值均大于上、下行干扰,因而f-k域中正、负波数域内均有分布,且谱值特征更靠近f轴并关于f轴对称.
图3(c)是利用常规f-k滤波方法进行处理后得到的雷达剖面,f-k滤波器采用扇形滤波器,选取的滤波参数为2 000 MHz的频率上限和0.06 m/ns的视速度下限,主要保留f-k域内视速度大于0.06 m/ns 的信号. 经滤波处理后得到图3(c)所示的雷达剖面图,如图所示,雷达剖面中的上、下行干扰均得到了有效压制,双曲线反射虽得到保留,但曲线两侧形态发生改变且能量有所衰减.
根据模拟数据f-k域频谱特征的分析,将f-k域内双曲线信号频谱特征外的上、下行干扰的频谱特征进行框选,得到了如图3(b)虚线区域所示的滤波区域.由于正、负波数域内的线性干扰频谱特征相同,因而该滤波区域关于f轴对称,该滤波区域内视速度上限为0.65 m/ns.
图3(d)是利用改进的f-k滤波方法,采用图3(b)所示的滤波区域,对线性干扰的f-k频谱特征进行处理后得到的雷达剖面图. 如图3(d)所示,两侧金属物体产生的线性干扰得到了有效压制,圆形空洞产生的双曲线仍有清晰的反映. 将图3(c)与图3(d)进行对比,发现常规的f-k滤波方法和改进的f-k滤波方法均能有效压制模拟数据中的倾斜线性干扰,但改进的f-k滤波方法保留有效信号的效果更好.

图3 数值模拟结果及f-k滤波对比
4 数值模拟及f-k滤波结果对比
测区为贵州某小型封闭岩溶洼地(见图4),洼地形如“碗”状,底部呈不规则的圆形,直径约46 m,洼地四周侧壁较陡且倾斜角度不一致,目测均大于30°. 洼地内表层为粘土层,其下为灰岩层. 采用SIR-20探地雷达及100 MHz 天线在洼地内部进行岩溶探测,在所采集到的东西向与南北向雷达剖面中均出现了由洼地四周侧壁产生的强烈空间干扰. 本文选取了其中沿洼地南北向长测线得到的雷达剖面(见图5)进行研究.

图4 岩溶洼地示意图
如图5(a)所示,洼地四周侧壁产生的空间干扰在雷达剖面表现均为具有不同反射强度、不同倾向、不同视速度的倾斜线性干扰. 在该剖面中,明显可见一条能量强的下行干扰,大致由雷达剖面(4 m,45 ns)处起始,到剖面中部(26 m,174 ns)处截止,视速度约为0.17 m/ns,推测该干扰是由测线起始处、洼地南面的侧壁产生. 此外,在图5(a)明显可见多条不同的上行干扰,其中,剖面底部(17 m,250 ns)和(23 m,210 ns)处有两条长度短、能量较强的干扰,其视速度相近,约为0.15 m/ns,推测可能是测线17 m、23 m 附近两侧洼地侧壁产生的;剖面(30 m,160 ns)至(41 m,57 ns)处有一能量强的上行干扰,其视速约为0.11 m/ns,推测可能是由测线终止处、洼地北部侧壁产生;剖面右下部可见能量弱的多条上行干扰,其视速度大体近似,在0.16 m/ns 左右,推测可能是由位于洼地南面的测线两侧边坡侧壁产生的.
图5(b)是对实测数据进行f-k变换后得到的f-k域频谱特征图,明显可见正、负波数域内频谱特征存在差异. 在图5(b)中,明显可见两条以原点为起点、谱值较大的谱值射线,其中f-k域中正波数域内为下行干扰的反映,负波数域内则为能量强的上行干扰在f-k域的反映. 同时,由于下行干扰视速度值大于上行干扰的视速度值,因而下行干扰的谱值射线斜率更大,相对上行干扰的谱值射线斜率更靠近f轴. 图5(b)中还可见正、负波数域内还存在一些不以坐标原点为起点、谱值较小的谱值射线,为实测数据中其他能量较弱的上、下行干扰在f-k域中的反映. 此外,实测数据中地下异常体反射的有效信号受各种噪声的干扰,在f-k域中的表现并不明显,而线性干扰的频谱特征相对更突出. 在岩溶洼地中,溶洞、破碎带等异常体的反射信号的视速度值通常大于线性干扰的视速度值,因此在f-k域中的频谱特征相对线性干扰的频谱特征会更靠近f轴.
图5(c)是利用常规f-k滤波进行处理后的雷达剖面,f-k滤波器采用扇形滤波器,滤波参数中频率上限为200 MHz,视速度下限为0.4 m/ns,主要保留f-k域内视速度大于0.4 m/ns的信号. 经滤波处理后,剖面中线性干扰的能量得到了衰减,可见剖面中部出现溶洞反映,但剖面中的线性干扰仍清晰可见,且在剖面(15 m,110 ns)和(37 m,100 ns)范围产生了新的干扰.
根据实测数据f-k域频谱特征的分析,在保留f-k域中f轴附近频谱信号的情况下,对f-k域中上、下行干扰代表的频谱特征进行框选,选择了如图5(b)所示的滤波区域. 由于f-k域中正、负波数域内频谱特征不同,故正、负波数域内的滤波区域也有所不同,其中正波数域内滤波区域视速度上限为0.42 m/ns,负波数域内滤波区域视速度上限为0.32 m/ns.
图5(d)是利用改进的f-k滤波方法,采用图5(b)所示的滤波区域,对线性干扰的f-k频谱特征进行处理后得到的雷达剖面. 如图5(d)所示,经滤波处理后,雷达剖面中的线性干扰得到了有效压制,且未产生其他强烈的干扰,中部的溶洞反映也清晰可见. 将图5(c)与图5(d)对比可看出,相对于常规f-k滤波方法,改进的f-k滤波方法对线性干扰的压制效果更好.
5 结论
常规的f-k滤波方法利用FFT 变换的复共轭特征,只对正波数信号进行处理即可得到全频域内的信号,忽视了实际数据中与正波数信号不同的负波数信号,因此虽能有效压制模拟数据中的线性干扰,但对实际数据中线性干扰的压制效果不理想. 对此,本文对f-k滤波方法进行改进,提出一种基于f-k域全域频谱特征的滤波方法. 在对雷达数据进行f-k变换后进行f-k全域分析发现,不同倾向线性干扰其视速度不同,因而在f-k域的频谱特征及分布区域存在差异. 基于这种差异,在f-k域正、负波数域内设计不同的滤波区域框选出线性干扰所在的频谱区域进行滤波,区别压制正、负波数域内线性干扰的频谱,达到压制雷达数据中线性干扰的目的. 通过模拟数据及实测数据的分析处理,与常规f-k滤波方法相比,改进的f-k滤波方法对线性干扰的压制效果更显著,对探地雷达剖面的处理效果更好.

