非理想观测下的多功能雷达工作状态在线切换点检测方法
鲍加迪,李云杰,朱梦韬,张 蔚
(1. 北京理工大学信息与电子学院,北京 100081;2. 中国电子科技集团公司第二十九研究所,四川成都 610097)
1 引言
多功能雷达(Multi-Function Radar,MFR)具有捷变的波束调度能力、复杂的信号调制样式、程控的工作模式编排,可以同时执行多个任务,被广泛应用于目标监视和跟踪领域. 定义实现特定雷达功能的发射脉冲序列为MFR 的工作状态,则电子侦察系统截获的MFR 脉冲序列可以包含数量未知的多个雷达工作状态,各状态对应脉冲组的脉内和脉间调制样式不同,持续时间也可能不同. 准确快速地对MFR 工作状态切换点进行在线检测对识别MFR 行为意图具有重要意义,这也已经成为现代电子战研究领域中的一个热点和难点问题.
近年来,研究者研究了多种MFR 工作状态识别和检测的方法. 文献[1]从非合作的视角将MFR 层次化描述扩展到了时间序列维度,提出的层次化序列到序列长短时记忆网络可以对包含多个雷达工作状态的输入脉冲序列,实现脉冲级的工作状态识别和状态间切换边界检测. 文献[2]提出了一种基于贝叶斯准则的MFR 切换点检测算法,通过直接对脉冲描述字(Pulse Description Word,PDW)进行处理,难以适应连续取值空间的捷变调制脉冲序列和非理想因素的情况.
序贯分析理论[3~5]自提出以来得到了长足的发展.文献[3]提出了统一的切换点检测算法框架,建立了序贯分析中切换点的数学模型,给出的虚警率和检测延迟概念成为之后切换点检测研究中评价检测器性能的指标. 切换点检测算法的成果已经在多个领域中得到广泛应用,包括电网监控[6]、传感器网络[7]、社交网络[8]、地震学[9]、视频监控[10]以及无线通信[11]等. 文献[12]首次将切换点检测应用于MFR 脉冲序列,通过检测幅度均值的切换得到模式切换检测结果,但未考虑缺失脉冲、虚假脉冲等真实电磁环境存在的非理想情况,以及雷达脉冲序列存在的复杂脉间调制类型. 为此,本文设计了一种适应非理想观测的多功能雷达工作状态在线切换点检测算法.
2 多功能雷达工作状态切换点检测问题建模
2.1 多功能雷达工作状态序列模型
MFR 系统的有效表征模型是实现状态切换点检测的基础.Visnevski 首次提出的MFR 的层次化模型[13]和后续提出的用于雷达资源管理的MFR 句法表征模型[14],被国内外MFR 行为建模与识别研究界广泛引用[15~20].
已有基于系统功能维度建立的MFR 的层次化模型中,组成最底层“符号-脉冲”层的脉冲序列对应的脉间调制都比较简单,如文献[13]中的雷达字层和文献[21]中的雷达字、雷达音节和雷达字母层. 随着先进体制MFR 及新一代认知MFR 的发展,雷达系统可以在“符号-脉冲”层次的脉冲序列实现更多类别的复杂脉冲序列调制类型,每种调制类型可以实现更灵活的参数控制. 文献[22]中将MFR模型中的“符号-脉冲”层表述为雷达的工作状态,并进行了由“多参数定义的工作状态-状态定义参数的脉间调制类型-脉间调制类型的定义参数”三要素组成的层次化表述. 文献[23]进一步从数学上将雷达工作状态由对应的调制类型空间和调制参数空间表征.
本文基于上述扩展后的层次化工作状态模型,以单PRI(Pulse Repetitive Interval)参数抖动调制定义的MFR 工作状态为对象,研究非理想观测条件下实现调制参数粒度的工作状态切换点检测算法.
2.2 多功能雷达PRI参数的抖动调制模型
本节给出2 种典型抖动PRI 调制类型的参数化模型以及PRI观测序列中典型非理想条件的表征方法.
2.2.1 典型的PRI序列抖动调制模型
(1)PRI序列的高斯抖动调制
高斯抖动分布的模型参数为均值μ和方差σ2. 输入PRI序列Y=(Y1,Y2,…,Yn)中Yt的概率密度分布为

其中,Φ(μ/σ)为正态累计分布函数. 该分布的对数似然函数为

μ和σ2的最大似然估计为
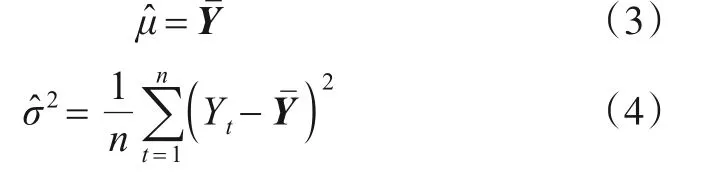
(2)PRI序列的均匀抖动调制
均匀抖动分布的模型参数为抖动上界a和抖动下界b. 输入PRI 序列Y=(Y1,Y2,…,Yn)中Yt的概率密度分布为
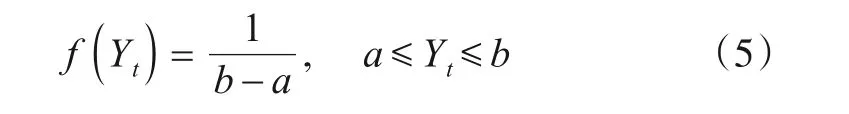
脉冲PRI在一个数据段内服从均匀分布,对数似然函数为

上下边界参数的最大似然估计为

2.2.2 PRI序列的非理想观测表征
雷达信号“发射-传播-接收”过程中的各种因素将会给使得侦察接收机截获侦收的MFR 脉冲序列出现测量误差、虚假脉冲、缺失脉冲等非理想情况,形成非理想观测样本,如图1所示.
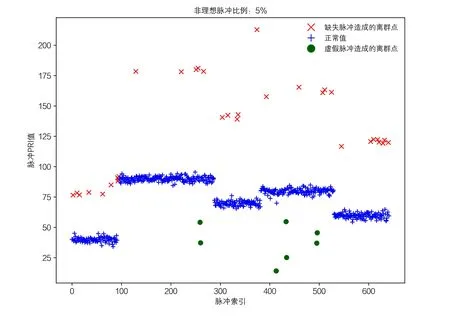
图1 虚假和缺失脉冲的影响
测量误差指的是对PRI数值的测量误差,本文使用常用的高斯分布噪声来表示PRI 的测量误差. 虚假脉冲指的是接收信号中不属于目标辐射源的干扰脉冲信号,本文定义虚假脉冲率(Spurious Pulse Rate,SPR)参数,对序列样本中的虚假脉冲占比进行控制. 缺失脉冲指的是目标辐射源脉冲信号出现丢失的现象,本文定义缺失脉冲率(Lack Pulse Rate,LPR)参数,对序列样本中的脉冲缺失占比进行控制.
这里需要注意,PRI 数值由脉冲到达时间(Time Of Arrival,TOA)参数进行一阶差分(Difference of first or⁃der Time Of Arrival,DTOA)运算得到,虚假脉冲和缺失脉冲对截获信号PRI序列的影响如图1所示. 虚假脉冲会在DTOA 计算中带来小于真值的虚假“PRI”数值,而缺失脉冲会带来大于真值的虚假“PRI”数值.
2.3 多功能雷达工作状态切换点检测问题
2.3.1 工作状态切换点定义
假定接收到的MFR 脉冲PRI 数值序列服从概率密度分布函数pθ(Yt),t为离散时间下标,θ是概率密度分布函数参数. 本文将满足下面条件的时刻t0定义为MFR 的工作状态切换点:时刻t0前后的概率分布函数pθ(Yt)相同,但是概率密度函数(Probability Density Function,PDF)参数不同,即θ≠θ1且满足:

2.3.2 多功能雷达工作状态切换点检测问题
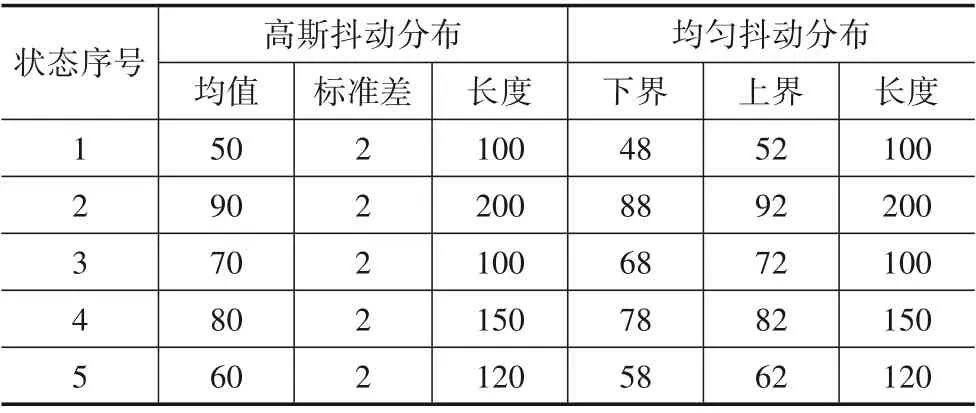
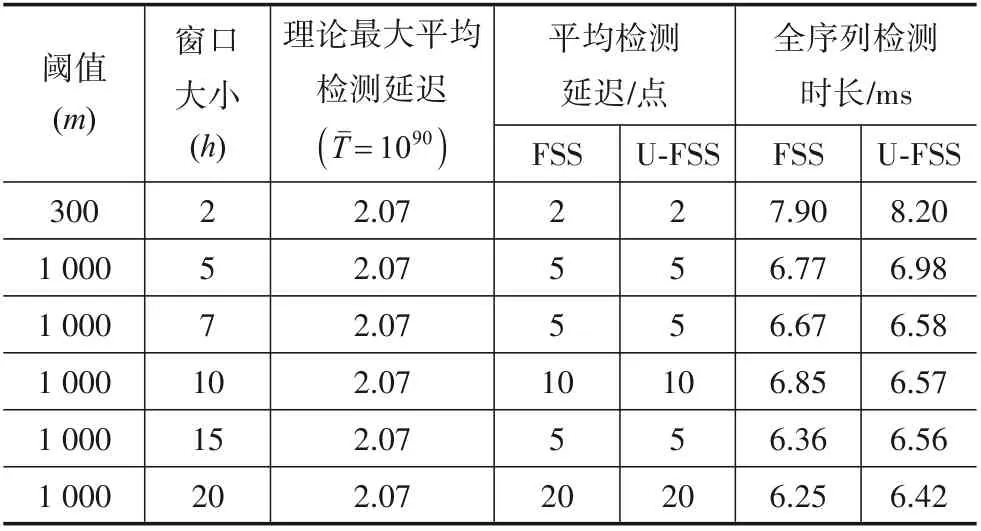
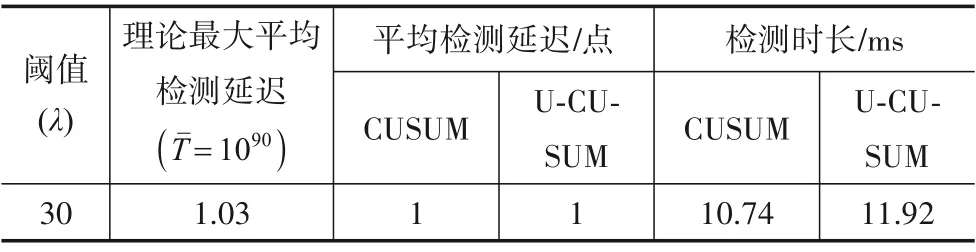
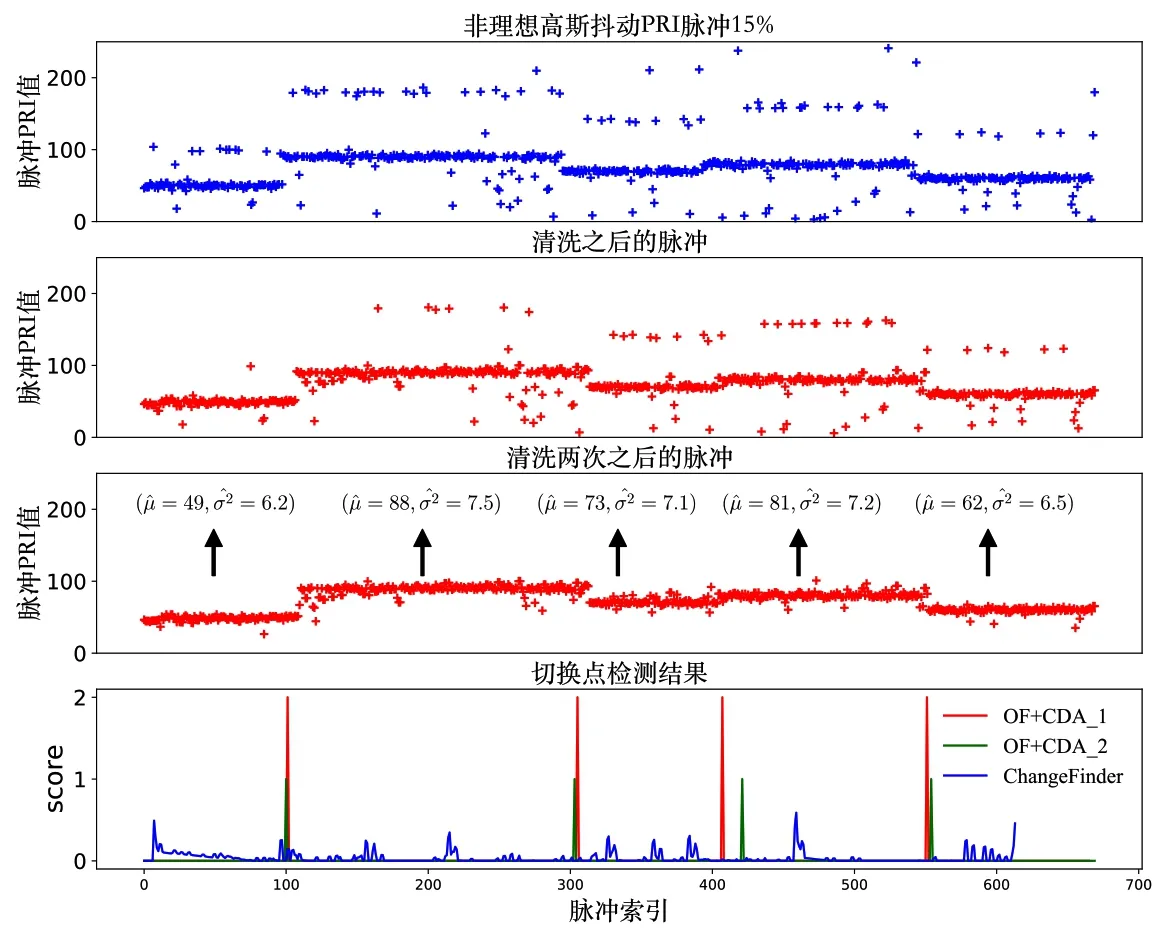
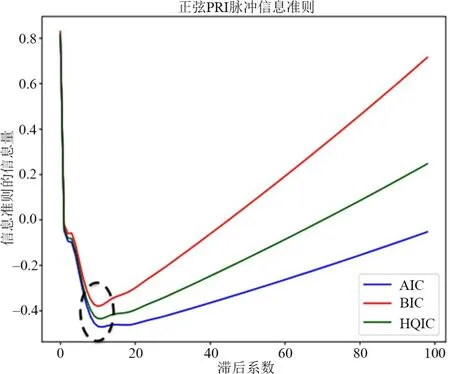
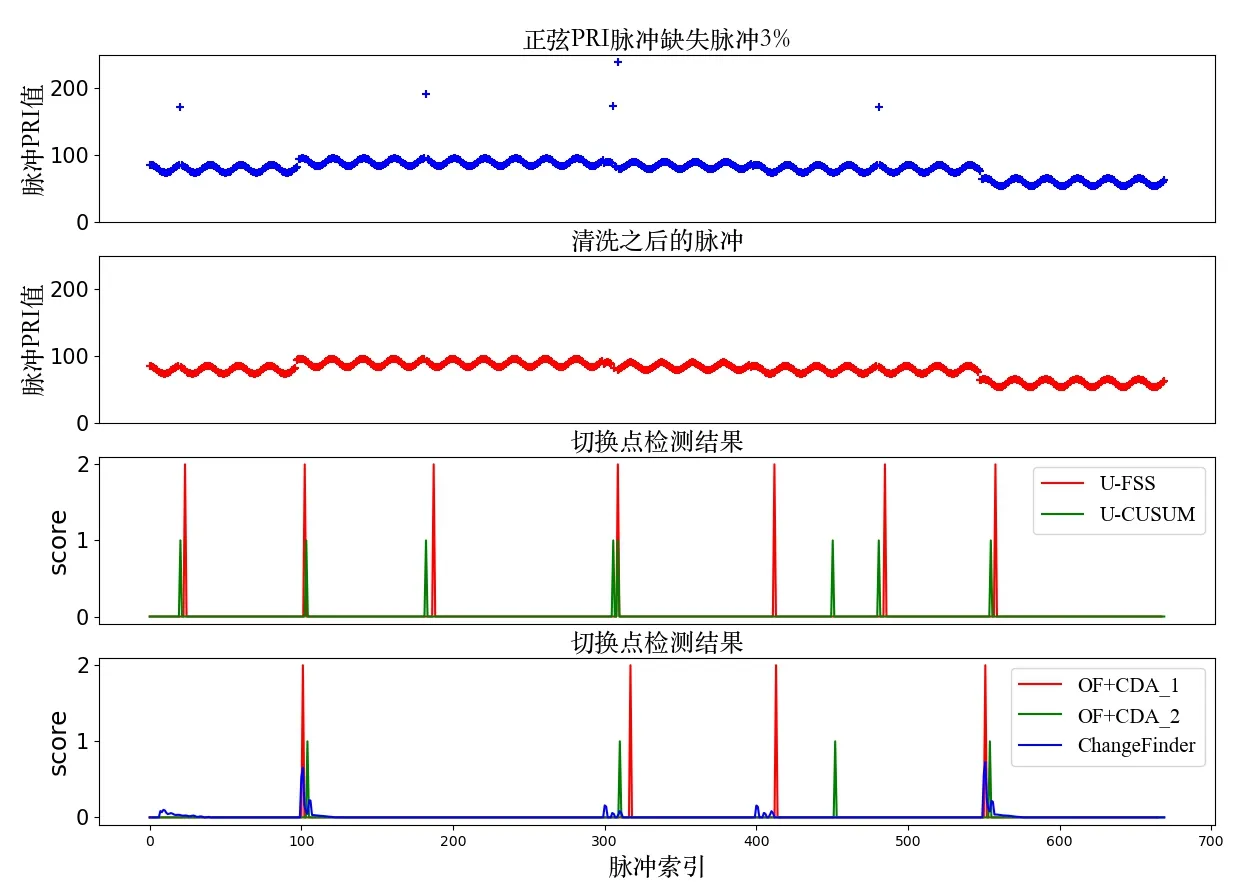
假定长度为L的脉冲序列(Yt)L≥t≥1中存在的切换点数目K未知但数目有限(1 R就表示了对(Yt)L≥t≥1的分割,K个切换点对应K+1 个片段,每个分割片段对应的概率密度分布记为pθk(Yt),1 ≤k≤K+1.MFR 切换点检测问题可以描述为:基于序贯到达的(Yt)L≥t≥1,同时估计R和pθk(Yt). 检测算法的灵敏度可以使用最坏情况平均检测延迟量(“worst case”average detection delay)τ*来表示[24]: 其中,t0为真实切换点的位置,N为算法检测到切换点的位置,esssup为本性上确界. 本文设计的非理想观测条件下的MFR 工作状态切换点检测处理流程如图2所示,主要包括模型更新和参数估计、离群点检测处理、切换点在线检测等3个步骤. 图2 适应非理想观测的MFR工作状态切换点检测框架 整个处理框架的输入信号为雷达脉冲序列,需要设置的参数包括自回归(Auto Regressive,AR)模型滞后系数K,以及参数未知的定长取样(Unknown-Fixed-Size-Sample,U-FSS)算法的参数Θ=(m,h),参数未知的累积和(Unknown-CUmulative SUM,U-CUSUM)算法的参数λ. 处理框架的输出为切换点指示矢量R. 针对虚假脉冲和缺失脉冲等非理性情况造成的离群值,本文设计了基于模型估计实现离群点检测和剔除的非理想观测中离群值剔除(OutlierFinder,OF)算法. 其中,K为AR 模型的滞后系数,每一个Ai都是一个n阶方阵,σ是多元高斯随机变量,均值为0,协方差为Σ,可以表示为N(0,Σ). 最优滞后系数通过偏自相关图来构建[25]. 对应滞后系数的好坏可以采用赤池信息准则(Akaike Information Criterion,AIC),贝叶斯信息准则(Bayesian Information Criterion,BIC)或者HQ 信息准则(Hannan-Quinn Information Criterion,HQIC)来衡量,信息准则的值越小,模型越好. 第二步是离群点检测处理. 依据式(14)所示的对数损失函数对检测点的后验概率密度函数进行负对数打分. 然后将打分与预先设置的离群点检测阈值进行比较,若打分值大于该阈值,则判定当前检测点为离群点. 为了消除离群点影响,若该时刻脉冲值大于AR 模型的预测值,判定发生脉冲缺失,选用AR 模型预测的结果对数据进行插值;若该时刻预测脉冲小于估计值,判定出现虚假脉冲,直接将虚假脉冲进行删除,完成对序列的重构. 针对重构消除了缺失脉冲和虚假脉冲后的输入脉冲序列,本节给出适应切换点前后序列分布参数未知情况下的切换点检测算法U-FSS 算法和U-CUSUM算法. 3.3.1 U-FSS算法 本文设计了改进的U-FSS 算法(记为CDA_1). UFSS采用了最大似然估计来估计未知参数,其中广义似然比可以写为 最大似然估计的方式采用第2.2.1节中阐述的式(3)、式(4)和式(7)、式(8)进行估计,将估计值与观测值的累加似然比和阈值进行比较,如式(16)所示. 累加似然比按照下式进行计算: 定义决策函数为 则N为检测到的切换点的判别,即 式(17)和式(18)采用固定窗口m对序贯输入的数据进行划分,并计算每个脉冲窗累加似然比. 当累加似然比超过阈值h,则判定当前处理窗口的窗尾时刻为切换点. 3.3.2 U-CUSUM 算法 本文将参数估计与在线切换点检测结合起来,设计了改进的U-CUSUM 算法(记为CDA_2),其中参数估计的方法与CDA_1 算法中参数估计如式(3)、式(4)和式(7)、式(8). 在线切换点检测采用累加似然比与阈值λ比较来实现. 每读取一个新的时刻t的脉冲,累积和(CUmula⁃tive SUM,CUSUM)算法采用了一个变量i,i=k,k+1,…,t进行似然比的累加. 该操作可以学习之前所有脉冲序列的特征,用于切换点判决. 累加似然比Stk按式(16)进行计算,记N为检测到的切换点,如式(19)所示. 其中,λ为累加似然比的阈值,算法的误警率与阈值的设定有关. 式(11)所给的“最坏情况”平均检测延迟量τ*可以作为算法灵敏度的评价指标,τ*越大,灵敏度越低,τ*越小,灵敏度越高. 本文所提切换点检测处理方法的灵敏度分析如下所述. 首先,采用OF 算法对非理想观测序列中的实现离群点检测剔除,算法实现参数为滞后系数k,在重构序列的时候最多会导致k位的检测延迟. 然后,采用U-FSS 算法或者U-CUSUM 算法实现切换点检测处理. 定长取样(Fixed-Size-Sample,FSS)算法的实现控制参数为窗长m和切换点报警阈值h;CUSUM算法的实现控制参数为切换点报警阈值λ. 定性分析来看,对于FSS 算法,增大处理窗长参数取值会使得检测算法灵敏度变差,m的窗长最多会导致m位的检测延迟;对于CUSUM 算法,切换点报警阈值过高,会因为需要更多的样点进行累计,使得检测算法灵敏度变差. 定量分析来看,可以通过对雷达工作状态的参数化建模表征,计算对应算法实现工作状态在线切换点检测时的理论延迟. 在理想无干扰脉冲的情况下,针对不同调制类型的切换点序列推导给出FSS算法与CUSUM 算法在进行切换点检测在渐近情况下的理论延迟结论:在最优算法参数设置的情况下,FSS算法的平均检测延迟τˉ*趋近于固定值[24],即 CUSUM算法理论最优平均检测延迟τˉ*[26]为 由式(20)和式(21)可知,由于CUSUM 算法对每个数据进行判决,其渐近最优灵敏度为FSS 算法的一半,灵敏度较高;但是这是以空间复杂度的增加为代价的. 本节以抖动调制的PRI脉冲序列为例,进行切换点前后调制参数未知且存在非理想观测条件下的MFR 工作状态切换点在线检测算法仿真实验. 实验数据集中的高斯抖动和均匀抖动工作状态序列均考虑4个切换点,对应状态序列中的分布参数设置如表1所示. 表1 抖动工作状态序列分布参数设置 切换点检测的对比算法为经典的CUSUM 和FSS算法[24],以及带有离群值处理的切换点检测算法Change⁃Finder 算法[27]. 仿真程序基于Python3 开发,仿真计算机处理器为Intel Core i5-1038 NG7 CPU@2.00 GHz,操作系统为macOS,所有检测时间对比均为绝对时间. 仿真实验的性能评价采用“平均效益-误警率”对抗图来表示,图中横坐标为误警率,纵坐标为平均效益.在不同误警率的条件下,平均效益高的检测器性能好. 误警率定义为错误报警在所有报警中的占比. 单个切换点效益值定义如下: 其中,t0为真实切换点,N为在给定的检测延迟范围内(本文设置为10)正确检测到的切换点的索引(有效报警). 4.2.1 理想观测序列的切换点检测实验 本节为无虚假缺失脉冲的理想情况下的算法性能对比实验,数据采用的是高斯抖动PRI脉冲数据集. (1)传统FSS算法和U-FSS算法对比实验 针对表1 中第一个切换点进行单切换点检测对比实验的参数设置和结果如表2 所示. 按照3.4 节结论,将足够大的Tˉ=1090代入式(20)计算得到实验数据集在渐近情况下的理论最大平均检测延迟为2.07 位. 不同m,h参数设置下,FSS算法的理论最大延迟相同. 表2 传统FSS算法和U-FSS算法的平均检测延迟 由表2 可知,相同检测阈值h和不同窗口长度m条件下,最坏情况的检测延迟为h. 当窗口设置较大时(m=20),可能会出现较为严重的延迟,实际应用中可以通过调节窗口大小优化灵敏度. 表2 第一行是算法参数调至最优情况下的检测结果,这时的最小平均检测延迟为2,小于理论最大平均检测延迟. 检测时长方面,对于相同数据集,FSS 算法的检测时长随窗口的增大而减小. 对比相同参数设置下的FSS算法与U-FSS算法检测时长,U-FSS 算法由于加入了参数估计的步骤,检测时长相较于FSS算法有一定增长. (2)传统CUSUM算法和U-CUSUM算法对比实验 U-CUSUM算法基于广义似然比检验的原理实现检测,算法的检测时间与U-FSS 算法不同,可以做到极低延迟的切换点检测. 表3 给出了CUSUM 与U-CUSUM算法的平均检测延迟实验结果. 表3 CUSUM与U-CUSUM算法的平均检测延迟 由表3 可知,U-CUSUM 算法由于增加了参数估计的步骤,在子序列参数未知情况下进行切换点检测的平均检测时长相较于处理参数已知情况的CUSUM 算法要求更长,但是检测准确率并无明显变化. 平均检测延迟是算法参数调至最优情况下的检测结果,这时的平均检测延迟为1,小于理论最大平均延迟. 对比表2所给FSS 与U-FSS 算法实验结果,CUSUM 算法和UCUSUM算法的平均检测延迟相对较小. 4.2.2 非理想观测序列的切换点检测实验 非理想观测条件下的切换点检测实验具体包括“OF+CDA_1”“OF+CDA_2”“CDA_1/CDA_2”这3 类. 为了可视化效果,不同算法在各类实验中的得分结果在画图时乘以了相应的放大系数. (1)AR模型滞后系数选择 按照文献[28]所给方法计算得到OF 算法的最优滞后系数:高斯抖动PRI 数据集的滞后系数为3,均匀抖动PRI数据集滞后系数为2. (2)非理想观测条件下切换点检测性能实验 图3展示了在虚假脉冲和缺失脉冲比例均为5%的非理想观测条件下,对于PRI高斯抖动脉冲序列的清洗和切换点检测实验结果,均匀抖动的检测结果和高斯抖动的检测结果类似. 图3 非理想脉冲比例为5%时的数据清洗和切换点检测实验结果 图3 的子图3 是直接进行切换点检测的结果,包含有大量虚警. 子图4 为本文两种算法组合和用于对比的ChangeFinder 算法[27]的实验结果. 由图可知,本文所提方法可以准确地检测出真实的雷达工作状态切换点,极大程度地降低虚假缺失脉冲可能带来的虚警影响.“OF+CDA_1”的检测结果相较于“OF+CDA_2”的结果有一定延迟. 进一步,对于检测结果中仍然存在的少量虚警,可以通过调整阈值来缓解,或者对脉冲进行两遍清洗以增强脉冲清洗效果. 本文所提方法还可在检测到切换点后对雷达工作状态片段的调制参数进行估计,如图4 所示. 虚假脉冲和缺失脉冲比例分别为15%的非理想观测条件下,两遍清洗后的模型参数估计(子图3)和切换点检测结果(子图4). 均匀抖动的检测结果和高斯抖动的检测结果类似. 图4 非理想脉冲比例为15%时的切换点检测结果 3种算法对缺失脉冲和虚假脉冲比例均为5%的高斯抖动PRI 脉冲序列的“平均效益-虚警率”对抗图,如图5 所示. 由图可知,OF+CDA_2 方法检测系统在不同虚警率条件下的平均效益最高,OF+CDA_1 方法次之,而ChangeFinder算法由于对离群点过于敏感,平均效益最差. 更多实验结果表明,虽然虚假脉冲和缺失脉冲比例的增多会导致平均效益的下降,但是3种算法的相对性能结论几乎不变. 图5 平均效益-虚警率对抗图(高斯抖动序列5%虚假脉冲+缺失脉冲) 4.2.3 未知调制类型的切换点检测实验 针对难以用解析式表达或者位置调制类型的PRI脉冲序列,本文所提处理方法采用“最优拟合”策略进行应用. 首先采用3 种信息准则为脉冲序列推荐最优的AR 模型滞后系数,滞后系数增长的过程中,全局最小值对应的滞后系数为最优,所对应的AR模型也为最优模型. 以正弦调制的PRI 脉冲序列为例,用于最优滞后系数选择的信息准则计算结果如图6所示. 图6 AR模型拟合正弦PRI信息准则 3 种信息准则均在滞后系数为9 时,达到全局最小值. 采用该滞后系数对掺杂3%的缺失脉冲的正弦PRI进行离群值剔除以及切换点检测的实验结果如图7 所示. 由图可知,上述策略对于低缺失脉冲和虚假脉冲比例的正弦PRI有较好的清洗效果,能够较为准确的检测切换点. 图7 正弦PRI调制工作状态切换点检测结果(缺失脉冲3%) 4.2.4 显著切换点混淆误判的检测实验 首先给出显著切换点的定义如下:假设t为真实切换点,对应的PRI脉冲为Yt,若Yt-1 在显著切换点情况下,可能出现切换点和离群点误判. 分析可知,这种误判影响并不大,其结果是重构序列的切换点比真实的切换点后移最多k个脉冲点,上述结论的实验验证结果如图8所示. 图8所示的两个切换点均为显著切换点,离群点检测阈值为min(Score(2Yt),Score((1/2)Yt)),图中蓝色离群值打分曲线经过阈值比较,将切换点被错误的识别为离群点. 按照相应策略进行重构后,正确检测到了切换点,但存在一定延迟. 以U-CUSUM 算法为例,在第一个切换点导致了两个点的检测延迟,在第二个切换点导致了一个点的检测延迟. 图8 显著切换点检测仿真结果 准确快速地对MFR 工作状态切换点进行在线检测对识别MFR 行为意图有重要意义. 本文在MFR 工作状态层次化扩展建模基础上,提出了一种非理想观测下的MFR 工作状态在线切换点检测方法. 其中Outlier⁃Finder 算法可实现由于虚假脉冲和缺失脉冲造成的离群点的检测和清洗;改进的U-FSS 算法和U-CUSUM 算法实现无参数先验信息情况下的切换点检测与工作状态参数估计. 仿真实验验证了所提出算法和处理框架的有效性和优越性.
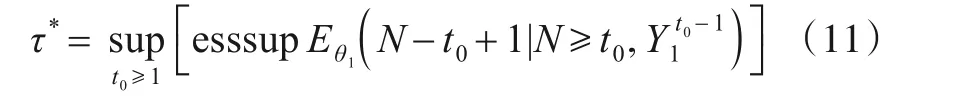
3 非理想观测下的MFR 工作状态切换点检测
3.1 工作状态切换点检测方法的总体流程

3.2 非理想观测中离群值剔除算法

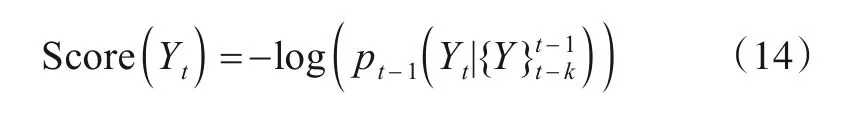
3.3 参数未知情况下在线切换点检测算法
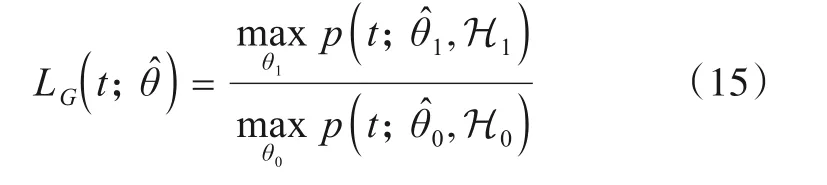
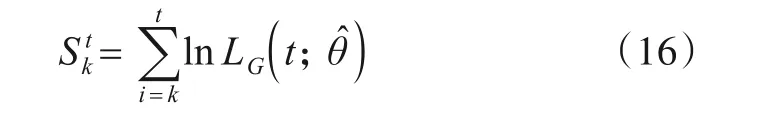
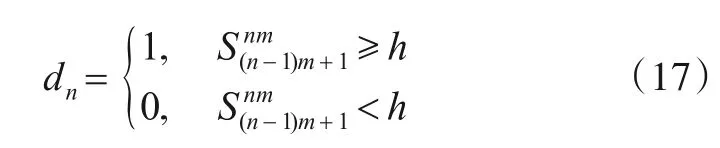

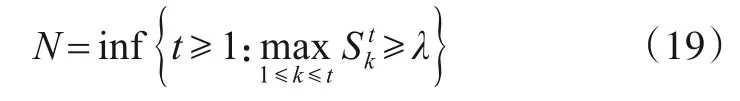
3.4 切换点检测处理流程的灵敏度分析



4 算法性能仿真分析
4.1 实验设计

4.2 实验结果分析



5 总结

