复杂系统中的气候变化和玻璃化转变

张建华,蒋哲华,童 华，徐 宁

(中国科学技术大学 物理学院 物理系，安徽 合肥 230026)

2021年诺贝尔物理学奖一半授予真锅淑郎(Syukuro Manabe)和克劳斯·哈塞尔曼(Klaus Hasselmann)，表彰他们关于“地球气候的物理建模、量化可变性和可靠地预测全球变暖”的工作；另一半授予乔治·帕里西(Giorgio Parisi)，表彰其“发现了从原子到行星尺度的物理系统中无序和涨落之间的相互影响”. 前者的工作奠定了气候模型的发展基础，并证明了温室效应是人类排放CO2的结果；后者的工作在无序的复杂系统中发现了隐藏模式，为人类理解和描述不同领域中的复杂材料和现象提供了可能方法. 本文从复杂系统的概念出发，对2021年诺奖获得者的代表性工作进行介绍.

1 复杂系统的典型特征

复杂系统无处不在，小到原子、分子系统，大到人类活动、气候变化以及行星的运动等. 到底什么样的体系可以被称为复杂系统呢？尽管复杂性科学已被用来理解蚁群行为、市场经济和气候变化等现象，但人们对复杂系统的基本定义仍未达成统一. 关于复杂系统，最著名论断来源于亚里士多德(Aristotle)，他认为复杂系统“整体大于部分之和”. 在复杂系统中，组元(部分)的集体行为将会表现出系统(整体)的某些宏观性质，而且这些宏观性质几乎无法从组元的属性中推断出来. 《Science》于1999年4月发行了关于“复杂系统”的特刊，下面将总结复杂系统的典型特征.

1.1 非线性

非线性通常被认为是复杂系统必不可少的条件之一. 如果系统是线性的，那么将系统的运动方程的任意多个解叠加或者任意解乘以1个因子可以得到其他解. 非线性意味着叠加原理将不再适用，系统的运动方程可能无法精确求解，只能得到近似解. 非线性带来的有趣结果是系统的发散，例如当位置和动量作为运动方程的输入参量时，初始条件的微小差异可能会导致最终结果的巨大偏差.

1.2 反馈机制

反馈机制是复杂系统的另一必要条件. 系统的一部分在接收反馈时如何与其邻居相互作用取决于早期该部分与其邻居之间的作用形式. 以迁徙中的候鸟为例，群体中的每只候鸟都有自己的路线，这取决于周围鸟类的方位和距离，但是如果某只候鸟调整了路线，那么其邻居都会改变飞行计划，因此，邻居的状态在一定程度上可反映该鸟的早期行为.

1.3 自发形成的序和鲁棒性

复杂系统研究的基本思想是探寻系统行为中的序，它是系统中大量基本元素之间相互作用的集中体现. 1950年，朗道(L. D. Landau)和金兹堡(V. L. Ginzburg)用序参量的概念来描述系统在相变前后的状态[1]. 在复杂系统中，由于可能涉及对称性、结构、周期性、确定性和模式等，因而系统序参量的定义并非易事. 复杂系统在外界扰动下会稳定存在，因此认为复杂系统具有鲁棒性. 地球气候变化是体现系统鲁棒性的典型例子，虽然局部的气候变化可能非常剧烈，但整体气候变化是相对稳定的，并具有规律性和周期性.

1.4 层展现象和层级结构

还原论的假设在哲学家中仍然是富有争议的话题，其基本思想是复杂的系统、现象可以通过将其化解为各部分之组合的方法，从而加以理解和描述. 人们谈论复杂性科学时常常将其与还原论的局限性联系起来. 20世纪科学的发展分为2种潮流：内涵性研究和外延性研究[2]. 内涵性研究探求基本定律，而外延性研究致力于按照已知的基本定律来解释现象. 安德森(P. W. Andeson)在批评科学界过于注重内涵性研究时指出：大量和复杂的基本粒子集合体的行为，并不能按照少数基本粒子性质的简单外推来理解. 事实上，在复杂性的每个层次，都会有崭新的性质出现，这就是层展现象. 在复杂系统中，通常有许多不同层级的结构，例如地球上的生态系统，不同层级结构包括群落、种群、个体、组织、细胞等.

1.5 多而不同

安德森强调层级结构对于理解复杂系统的重要性，指出整体不仅大于而且可能迥异于部分之和. 在每个层级上，新的定律、概念和原理都必不可少，并且其需要的想象力与创造力丝毫不亚于前一个层级，即量变产生质变. 上述讨论清楚地表明复杂性和复杂的系统并不简单，而且具有潜在的哲学意义. 下面以气候变化和玻璃化转变为例，讨论研究复杂系统的方法及重要意义.

2 气候变化

人类生活在正在发生重大变化的气候系统中，科学家们已经发现并证明了人类活动与气候变化的密切关系，例如大气中CO2浓度会导致气候变暖.

2.1 现代天气预报的建立

天气预报作为公共服务，已经渗透人们日常生活中. 最初天气预报的建立与战争有关，1853年-1856年英法等国与沙俄为争夺巴尔干半岛爆发了克里米亚战争[3]. 虽然战争以英法胜利告终，但英法联军在1854年11月的黑海战役中却损失惨重，原因是风暴突然降临黑海，海上狂风大作，巨浪滔天，英法舰队几乎全军覆没. 事后，法国军方要求巴黎天文台对这次风暴进行调查. 巴黎天文台台长勒维耶(U. Le Verrier)与世界各地的天文学家合作，收集气象报告，发现这场看似突然的风暴是有迹可循的，风暴自西向东运动，在到达黑海之前，已经影响了西班牙和法国等地. 经过思考分析后，法国建立了世界上第一个天气服务系统，现代天气预报由此诞生.

2.2 蝴蝶效应

美国气象学家洛伦兹(E. N. Lorenz)在 1961年的计算机模拟实验中发现初始条件的微小改变会导致结果的巨大差异. 洛伦兹研究大气对流的模型[4]如下：

(1)

其中，x为对流运动的强度，y为上升和下降气流的温度差，z为垂直温度曲线的线性偏差.控制参量普朗特数σ反映流体的物理性质，瑞利数Ra为与浮力驱动对流相关的无量纲数，β为表征空间几何性质的常量.

洛伦兹系统虽然简单，但为研究低维复杂系统提供了丰富的模型框架. 图1所示为该模型的数值解在相空间中的轨迹[控制参量(σ,β,Ra)=(10,8/3,33.5)]，可以看到数值解是有边界的.

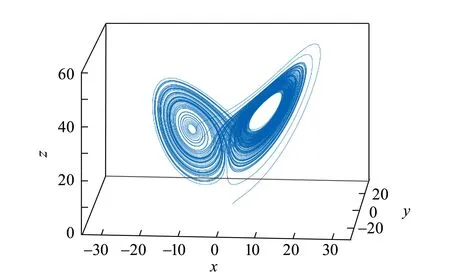
图1 洛伦兹模型的数值解的空间分布[5]

从图2可以看出该模型的解高度依赖初始条件时[控制参量(σ,β,Ra)=(10,8/3,24.9)]，初始时刻x仅相差0.1(图2中蓝线初始值为10，红线初始值为10.1)，随着时间的推移形成了巨大的偏差.

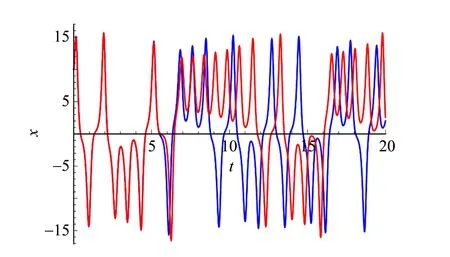
图2 洛伦兹模型的数值解x随时间的变化情况[6]

1972年，洛伦兹在科学会议上发表了题为“可预测性：巴西一只蝴蝶扇动翅膀，能否在得克萨斯州掀起一场龙卷风”的演讲[7]. 此现象被称为蝴蝶效应，即事物发展的结果对初始条件具有极为敏感的依赖性，初始条件的微小改变，可能导致完全不同的结果. 时至今日，蝴蝶效应的内涵远远超出气候变化的范畴，对社会、经济、哲学等诸多领域均产生了深远的影响. 蝴蝶效应也是复杂系统的典型示例，表明气候变化的长期不可预测性.

2.3 真锅淑郎和哈塞尔曼的工作

真锅淑郎的探究工作是大气中CO2浓度的增加是如何促使地球表面温度升高的. 1960年，真锅淑郎开展了对地球气候物理模型的开发与研究工作. 作为首个探索辐射平衡与气团的垂直输送之间相互作用的学者，该工作为气候模型的发展奠定了基础[8]. 真锅淑郎的模型 (图3)证实了大气确实是由于CO2浓度的增加而被加热.

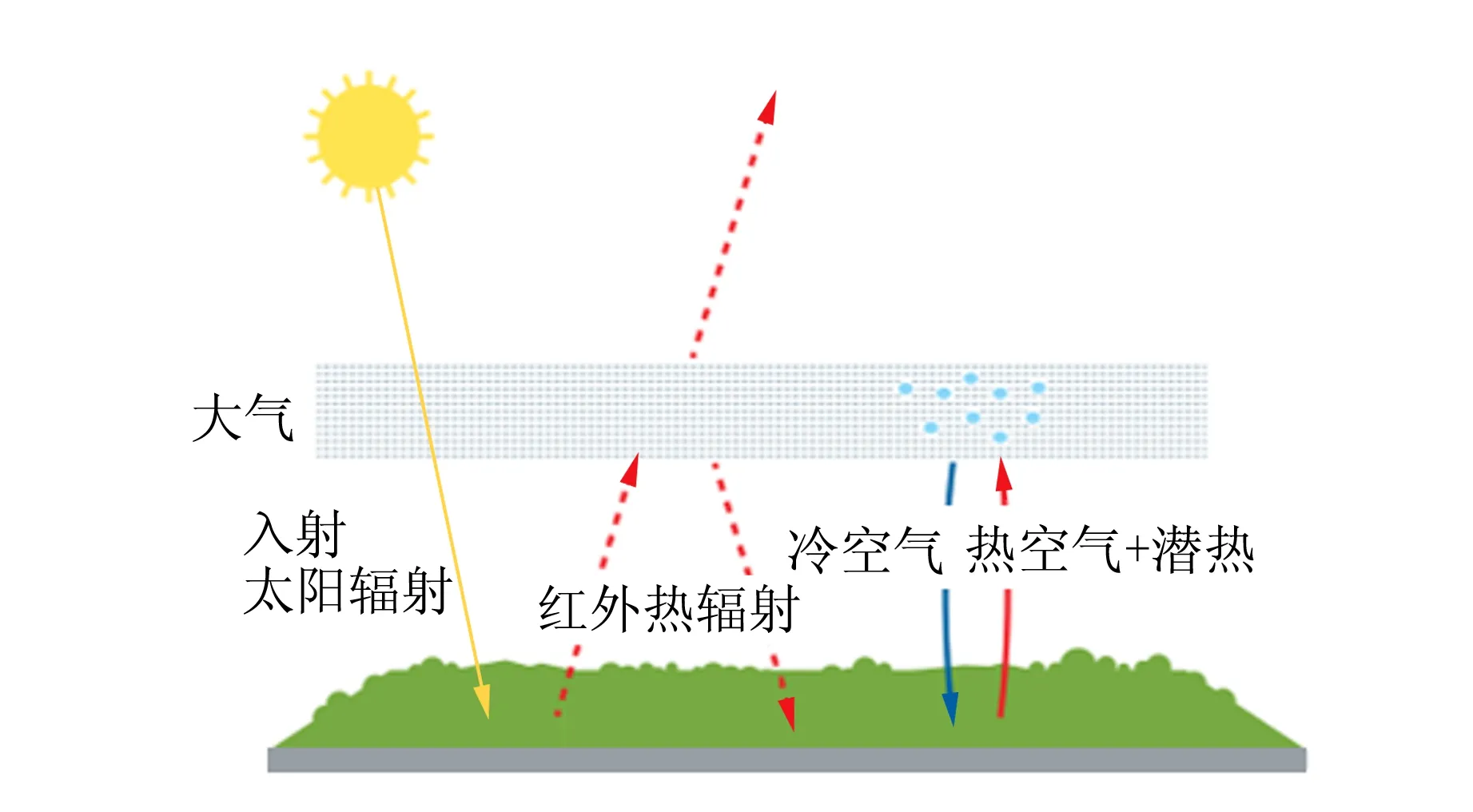
图3 真锅淑郎的气候模型[9]

地面接收到的太阳热量中，一部分以红外热辐射的形式向大气反射；经过大气层时部分热量辐射到外太空，部分反射回地面. 一方面，来自地面的红外热辐射部分被大气吸收，使空气和地面变暖; 另一方面，热空气比冷空气轻，通过对流会向上爬升. 热空气中还携带着水蒸气，水蒸气是一种强大的温室气体，空气越暖，其浓度就越高. 再往上，大气较冷的地方会形成雨滴，释放储存在水蒸气中的潜热[9]. 该模型预测出越靠近地面温度越高，越远离地面温度越低. 60年前，计算机的运行速度比现在慢几十万倍，只有相对简单的模型，才能进行计算模拟. 真锅淑郎的一维模型虽简单但却抓住了关键，从一维模型出发，真锅淑郎于 1975 年发表了三维的气候模型，成为了解气候道路上的又一里程碑[10].

大约10年后，哈塞尔曼建立了将天气和气候联系起来的模型，进而回答了为什么气候模型在天气多变且混乱的情况下仍然可靠的问题[11]. 哈塞尔曼的方法已经被用于证明人类排放的CO2确实是大气温度升高的原因.

天气是非常复杂的. 通过创建随机气候模型，哈塞尔曼成功地将天气和气候联系起来，向人们展示了如何将混乱变化的天气现象描述为快速变化的随机过程，从而为长期气候预测奠定了坚实的科学基础. 完成气候变化模型后，哈塞尔曼还开发了可以识别自然现象和人类活动在气候中留下印记特定信号和独特标记的方法[12-13]，即识别人类对气候影响的方法，使得人们可以单独观测人类对气候影响的痕迹.

3 玻璃化转变

玻璃质材料在自然和人类工艺中普遍存在[14]，已知的最早类似玻璃的釉料出现在大约公元前12 000年的埃及. 距今5 000多年前人们已经佩戴纯玻璃制作的护身符. 玻璃是人类制作使用最早的人造材料之一，人们对玻璃的认知和应用仍在不断更新. 玻璃同时具有固体和液体的特性，一方面，玻璃和固体都具有刚性；另一方面，玻璃和液体在微观粒子层面上都具有无序结构. 这种混合的特性使得玻璃的研究更加复杂.

3.1 玻璃的形成

一般通过对液体降温到玻璃化转变温度Tg以下制备得到玻璃. 需要注意的是，制备过程中的降温必须足够快从而避免液体结晶. 图4所示为恒定压强下，液体的体积和能量对温度的依赖关系. 液体降温至结晶温度Tm以下时，粒子运动开始变缓，进入过冷液体区. 继续降温，粒子重排变得非常缓慢，导致液体不能被充分取样，液体的结构在实验时间尺度上出现冻结，该过程被称为玻璃化转变，最终产生的物质就是玻璃. 降温速率越慢，液体在各个温度下的弛豫时间就越长，结果导致Tg随降温速率增加而增加. 降温速率较慢时在Tga处发生玻璃化转变，降温速率较快时在Tgb处发生玻璃化转变[14]. 因此玻璃的性质依赖于制备过程.

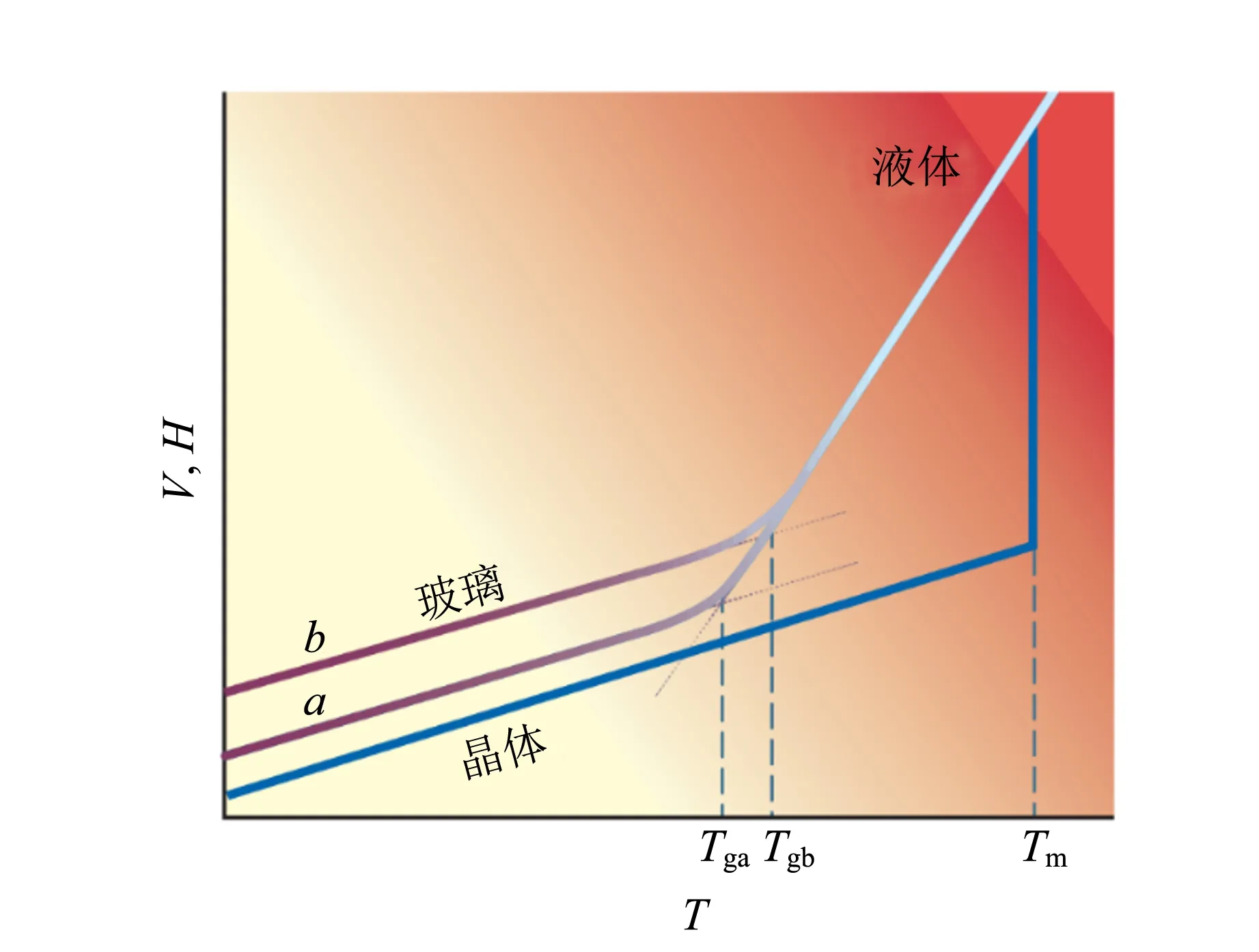
图4 液体体积和能量对温度的依赖关系[14]

研究发现，Tg对降温速率的依赖比较小(降温速率变化几个量级，Tg仅改变3～5 K)，因此，即使Tg不扮演相变温度的角色，也是重要的材料特性. 当降温至低于Tg时，物质仍会朝着平衡态缓慢演化，但在实验时间尺度上，物质永远无法达到平衡态，物质的物理性质随着时间缓慢演化，这个过程被称为老化(Aging).

黏度η是流体黏滞性的量度，是流体流动对其内部摩擦现象的一种表现. 在室温下，水的黏度较小，为10-2Pa·s量级. 实验上发现降温至Tg附近时，过冷液体的黏度快速增加，可以达到1014Pa·s甚至更高. 为了方便比较不同材料的性质，定义玻璃化转变为过冷液体黏度达到η(Tg) =1012Pa·s. 将黏度随温度变化的关系作图，横轴用Tg重新归一(Angell-画法)，如图5所示. 可以发现黏度对温度有很强的依赖关系. 在对数-线性坐标下，图5中的直线近似满足阿雷尼厄斯行为，这类体系被称为“强”过冷液体；下凹曲线满足超阿雷尼厄斯行为，称为“脆”过冷液体. 图中黏度的数值跨越了16个量级[15].

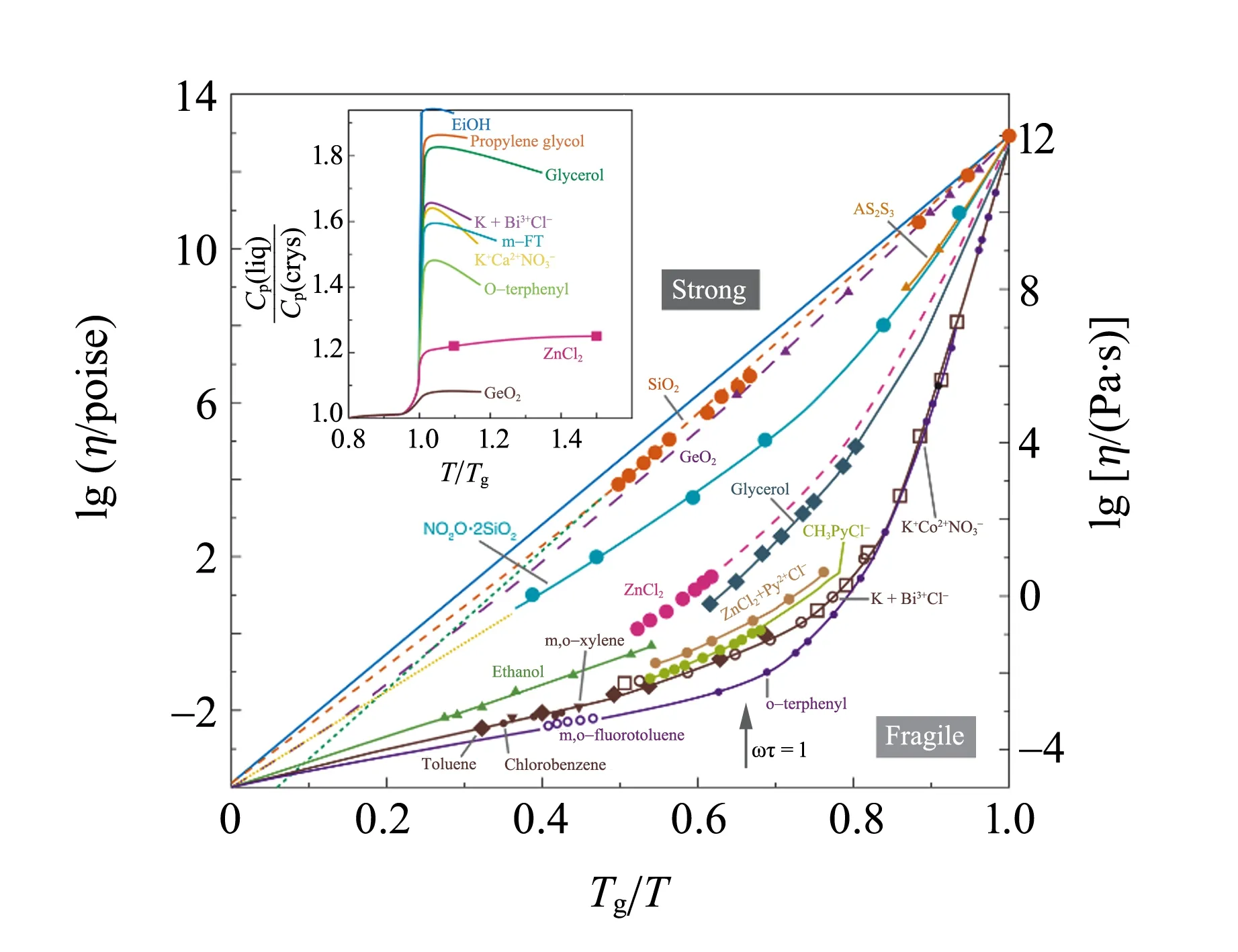
图5 不同过冷液体的黏度对温度倒数的依赖关系[15]

3.2 玻璃的典型特征

在传统凝聚态物理中，材料的结构决定其动力学. 例如，液体是无序的，因此可以流动和弛豫；晶体是有序的，因此不能流动和弛豫. 材料结构的改变会导致其动力学的变化，例如液体到晶体的热力学相变. 但是玻璃化转变显然不符合这一物理现象，由于其结构被禁锢，过冷液体的动力学变慢，但此时仍然维持液体结构. 这就在玻璃研究领域产生了非常基础的问题：玻璃化转变中观测到的结构禁锢只是动力学现象，还是液体到玻璃态的热力学相变导致的结果？玻璃化转变伴随着一些独特的现象，如何解释这些现象是所有玻璃化转变理论必须面对的问题.

3.2.1 动力学变慢

玻璃化转变前后，巨大的动力学变化可以用中级散射函数Fs(k,t)来表征

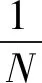
(2)

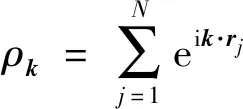
静态结构因子是连接实验分析与数值模拟的重要物理量，用来表征粒子位置的空间关联.图6所示为不同温度下伦纳德-琼斯系统的静态结构因子

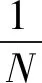
(3)

S(k)对温度只有微弱的依赖关系.如图6所示，在玻璃化转变温度附近，粒子运动变缓，最终被冻结，系统的动力学发生了巨大变化，弛豫时间τ增加了3个数量级，结构却几乎不变，这给理解玻璃化转变带来了更大的挑战.

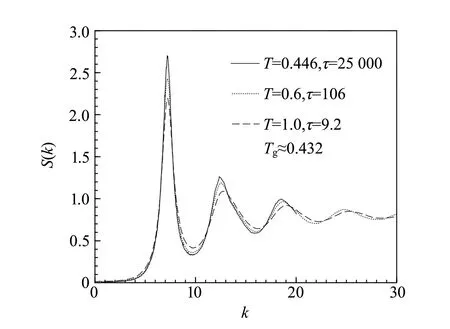
图6 伦纳德-琼斯系统的静态结构因子[16]

3.2.2 动力学异质性

随着温度降低或者密度增加，系统弛豫逐渐变慢.图7所示为二维过冷液体的空间轨迹图，其中粒子移动超过粒子直径标为深红色，粒子没有移动标为深蓝色.可以明显看到，移动快的粒子聚集在一起，移动慢的粒子同样聚集在一起.这是玻璃化转变的另一个典型特征——动力学异质性.

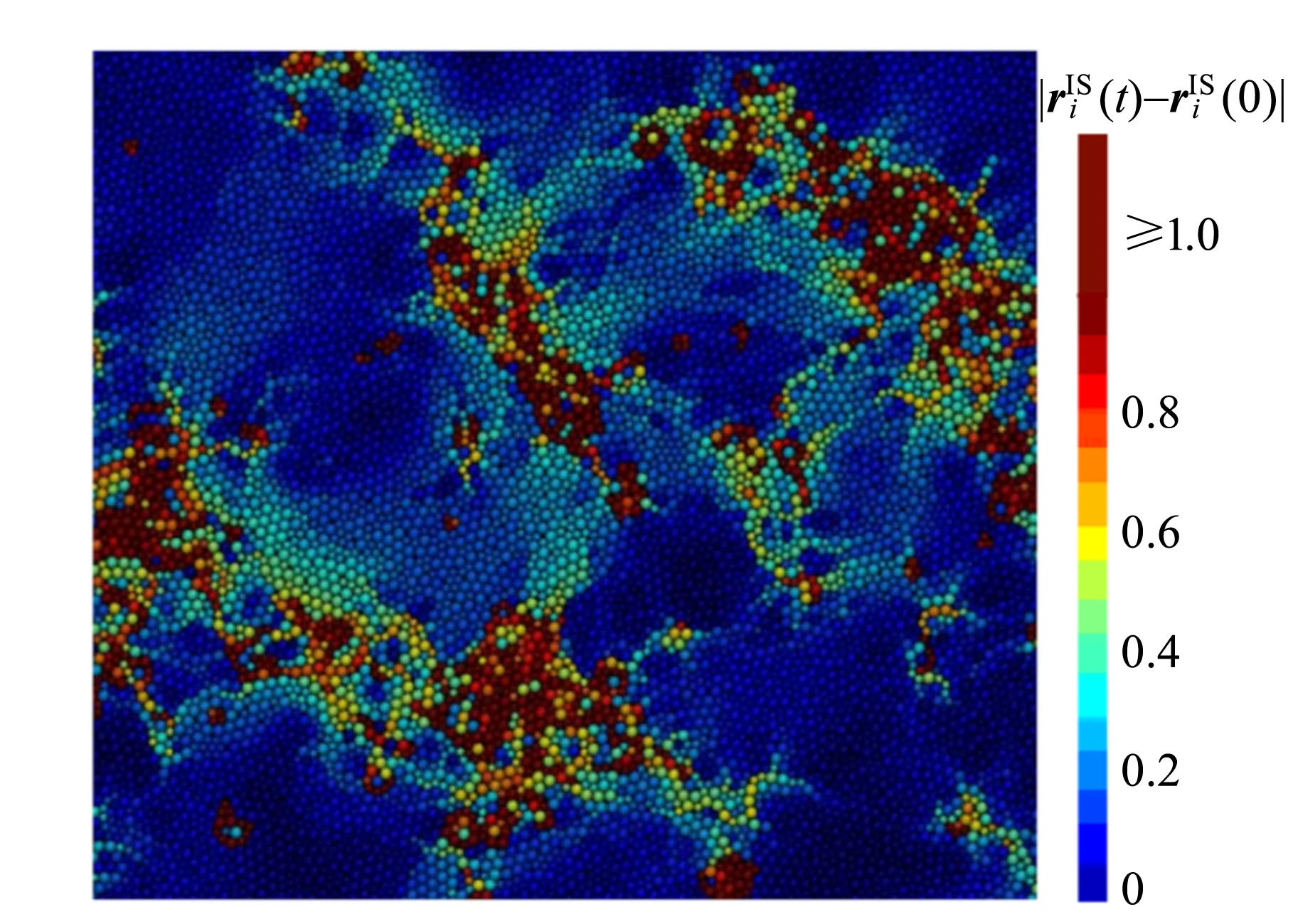
图7 二维过冷液体中的粒子轨迹图[17]

为了说明这一点，可以计算系统单粒子均方位移，Δi(t)=|ri(t)-ri(0)|2，结果如图8所示.系统的平均均方位移如图8中光滑的直线所示，而单粒子均方位移展现了系统在玻璃化转变温度附近的更多特征.可以发现，粒子的轨迹分为长时间围绕其自身的振动和由于动力学涨落而造成的快速跳跃.

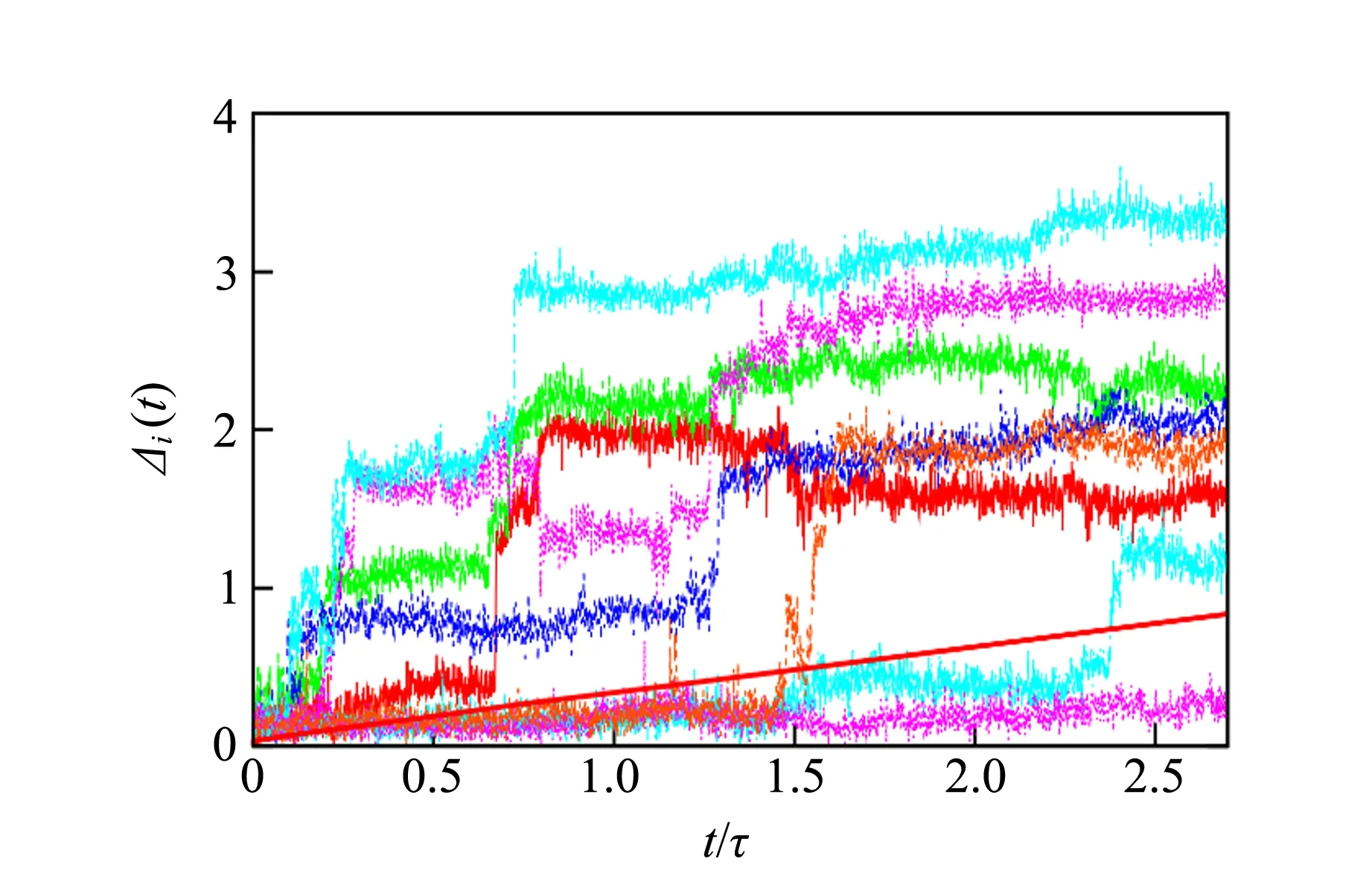
图8 系统在接近玻璃化转变温度时的单粒子均方位移图[18]

3.2.3 反常的热力学响应

邻三联苯是有机溶剂，因其易于形成玻璃态而在实验中被广泛使用.实验上发现邻三联苯在降温或者升温 (从过冷液体进入或者离开非平衡的玻璃态)过程中出现明显的滞回现象[19].如图9所示，在降温过程中，比热的值从液体区域下降到类似固体区域.比热的变化量ΔCp在某种程度上被看作玻璃形成能力的重要指标，也可以根据液体的弹性响应来理解.

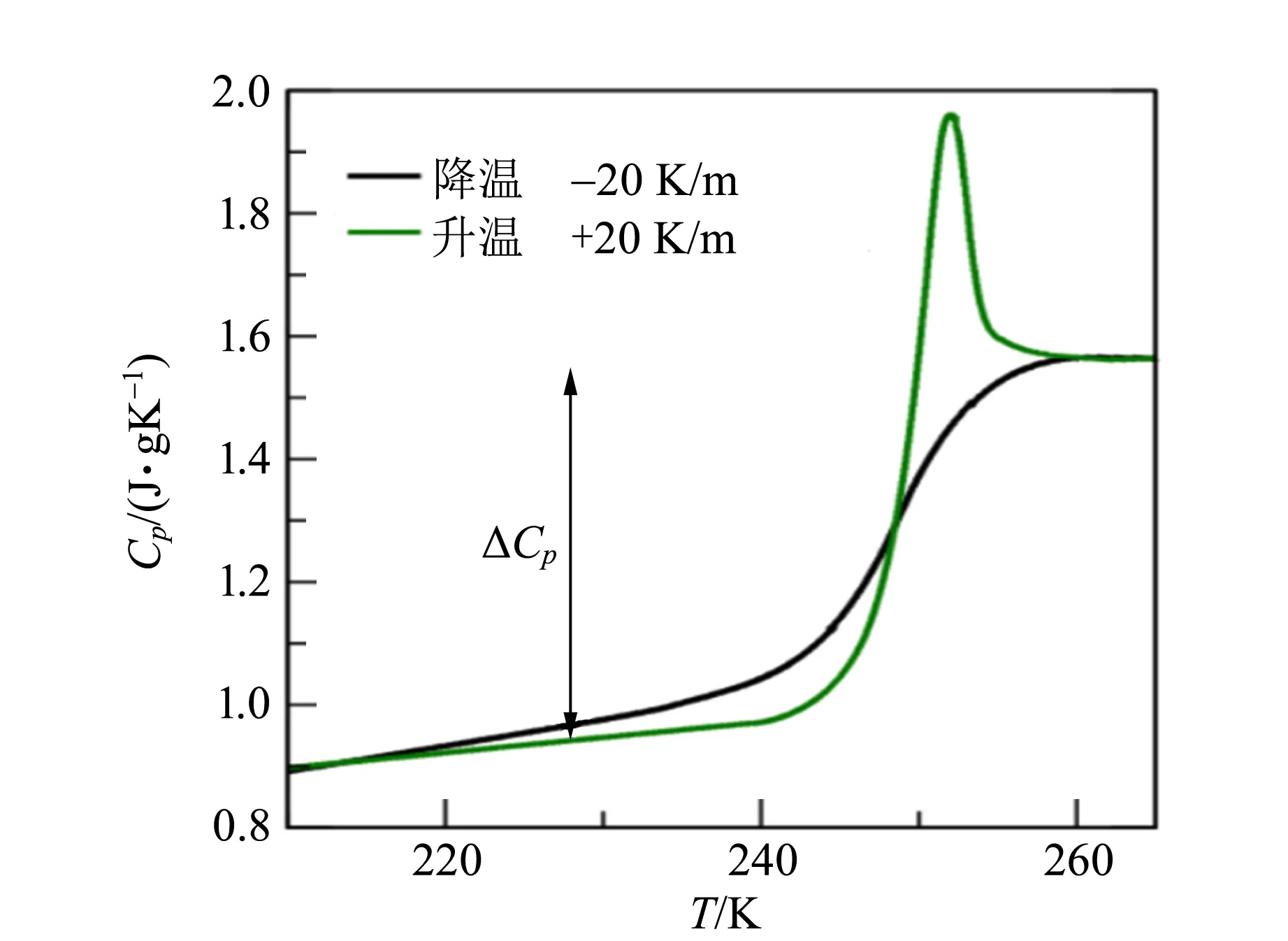
图9 邻三联苯的比热随温度的变化关系[19]

图9可以看出降温和升温过程中比热不对称.在升温过程中，比热曲线先出现1个峰再回到液体的值.这种不对称表明实验中观测到的液体到玻璃的转变是非平衡现象.其他热力学响应，例如比热容、折射系数等，也表现出类似行为.

3.3 帕里西的工作

3.3.1 自旋玻璃体系

自旋玻璃是本身无序，并且在转变温度Tf处出现冻结转变的一类无序磁性体系.自旋玻璃中的玻璃来源于其类似于玻璃化转变的、冻结的无序结构，并且这种无序性导致了相互冲突的磁矩排布，即阻挫.例如，用非磁性原子稀释近邻是铁磁相互作用，稀释次近邻是反铁磁相互作用的伊辛模型.这时带有磁性的原子随机扩散开来，使得磁性原子随机占据格点位置，形成自旋玻璃，如图10所示.在低温时(T0)，虚线表示次近邻间带有反铁磁相互作用(Jnnn<0).原来所有格点都有磁性原子，稀释得到自旋玻璃以后，磁性原子随机占据每个格点，并且导致局域自旋的阻挫.

图10展示了自旋玻璃相是无序结构的原因：单个磁矩周围的近邻和次近邻格点位置随机地被磁性原子占据，局域上看有的地方铁磁作用起效，有的地方反铁磁作用起效，形成阻挫，但总体加起来没有长程有序的宏观状态存在.阻挫现象是自旋玻璃的特征之一.

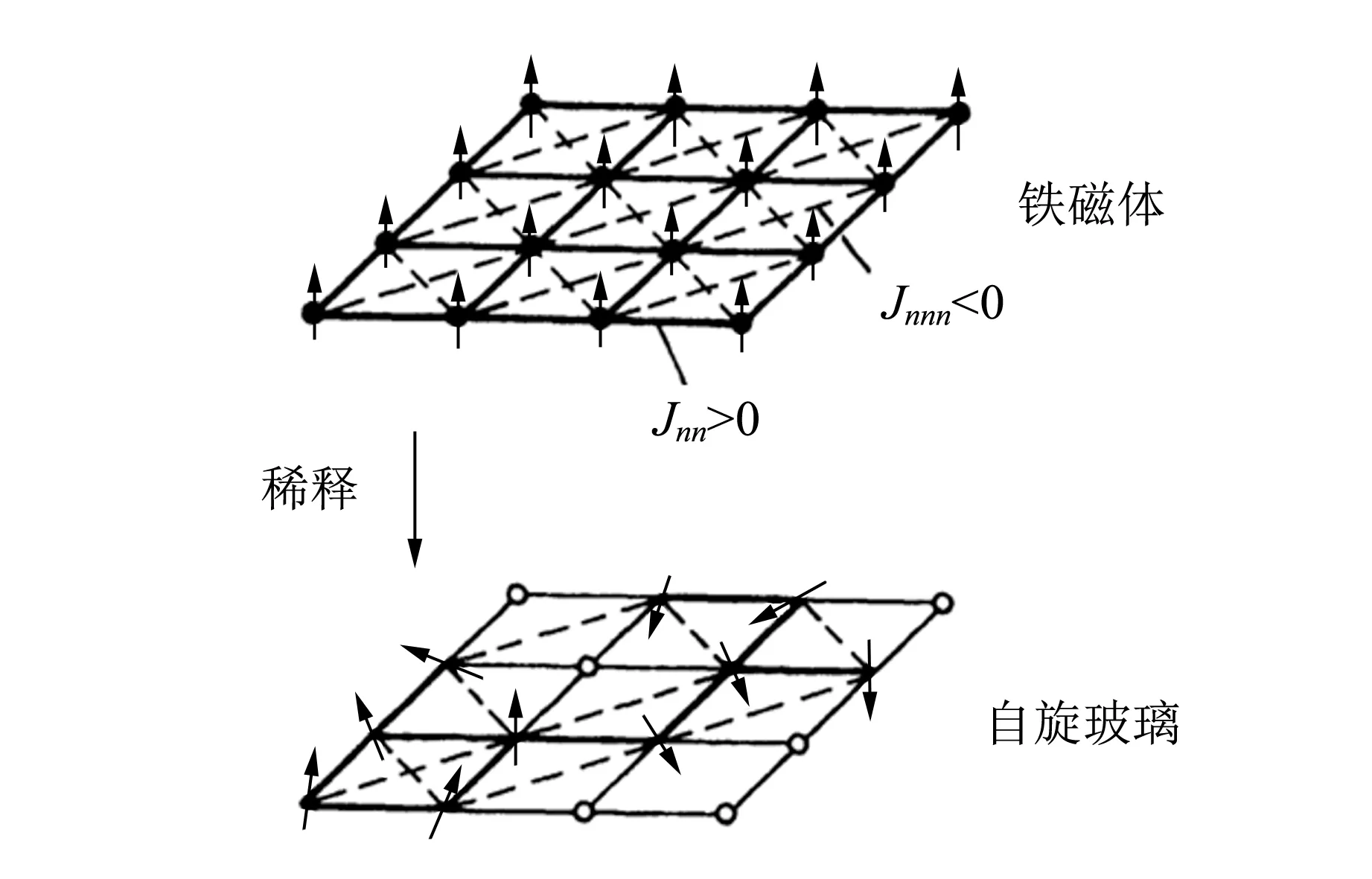
图10 铁磁体经过非磁性原子稀释后，体系从铁磁体转变为自旋玻璃[20]

用简单的例子来展现阻挫现象.如图11所示，在只有3个格点的伊辛模型中，施加小的外场，如果3个格点上的磁矩都满足铁磁相互作用，这时所有格点上的磁矩都朝向外场所指方向；如果磁矩满足反铁磁相互作用，图11中能量最低态需要所有相邻格点的自旋取向相反，那么无论如何搭配，均无法避免阻挫.例如，如果位于左下顶点的自旋方向向上，由于反铁磁相互作用，位于上顶点的自旋方向应该向下，这时位于右下顶点的自旋不论向上或向下，都无法同时满足另外2个已定的自旋方向.

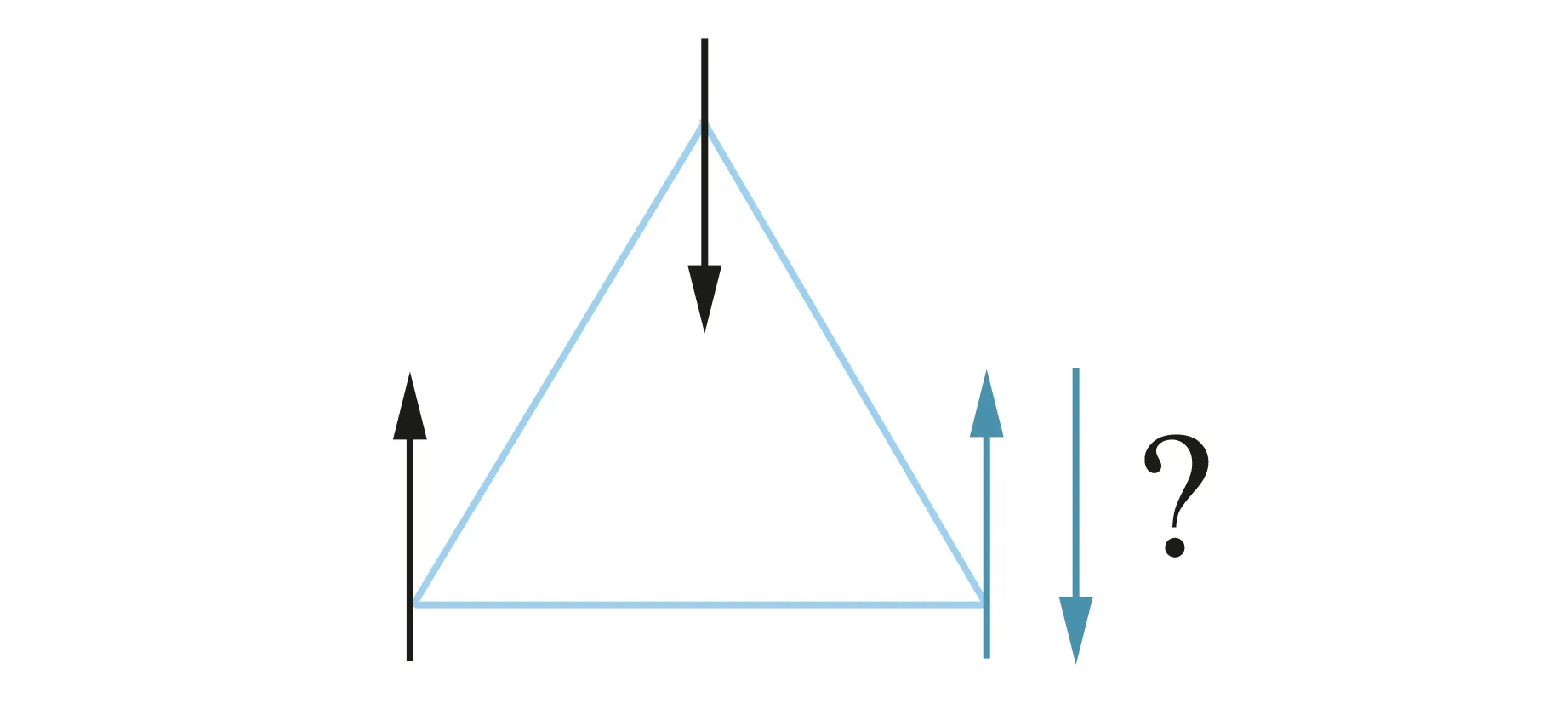
图11 三格点情况下反铁磁体展现出的阻挫现象[9]

相比于位置无序的结构玻璃体系，只有格点无序的自旋玻璃体系相对简单，但已经体现出复杂系统的诸多特性，也催生出了对于非平衡态系统的许多思考，因而从20世纪70年代开始，吸引了大批凝聚态物理学家的关注.

3.3.2 无序系统中的平均与副本方法

平衡态统计物理中，平衡态体系的弛豫时间远小于实验的时间尺度.因此，一般认为平衡态体系具有各态历经性，此时观测量的平均值既可以用时间平均，也可以用系综平均的方法得到，二者等价.

处在非平衡态的自旋玻璃，情况更加复杂.从3.3.1的论述中发现，自旋玻璃需要同时用自旋磁矩μi和磁性原子占据格点位置的随机变量xi来描述.对于某一观测量A，计算统计平均值时,先固定1组随机变量{xi}对应的位形，得到A的时间平均〈A〉T，然后用不同的{xi}产生的若干位形，进行位形平均[〈A〉T]av.

一般来讲，xi也可以发生涨落.当xi的弛豫时间远远小于实验观测时间时，无序带来的影响可以写入体系的哈密顿量中，配分函数可以写成简洁的形式，导致体系简化为纯的统计力学系统，外加带有无序的有效哈密顿量.这时观测量的统计平均与平衡态时的函数形式一样，这种平均被称为退火平均.例如体系的平均自由能F可以用

Fann=-kBTln [Z{xi}]av

(4)

来计算，其中Z{xi}为位形的配分函数.

如果xi的弛豫时间远大于实验观测时间，体系的无序结构被冻住，1个位形的随机变量固定在1组{xi}上不变，观测量只能采用[〈A〉T]av来计算，这种平均叫做淬火平均.此时式(4)变为

[F]av=-kBT[lnZ{xi}]av，

(5)

注意到这里是对lnZ进行位形平均.

在计算自由能的统计平均值时，位形平均作用在lnZ，而非配分函数Z本身上，这也是无序系统理论的困难之处.为了解决这个问题，爱德华兹(S. F. Edwards)等人提出了副本技巧[21-22]. 副本技巧依赖于

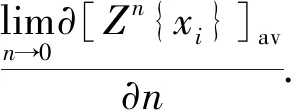
(6)

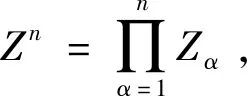
3.3.3 谢林顿-柯克帕特里克模型与副本对称解

从实验抽象出正确的理论模型需要考虑很多问题.如果模型太简化，可能无法定性地符合实验结果；太符合实际，又会因为过于复杂而无法求解.一般地，可以从相对粗粒化，同时略去许多微观细节的模型入手.爱德华兹和安德森于1975年开拓性地提出了爱德华兹-安德森模型[22]，指出自旋玻璃的模型可以基于伊辛格点模型，而格点的相互作用常量按照合理的分布给出，例如

(7)

(8)

通过3.3.2提到的副本方法，当n为正整数时，爱德华兹-安德森模型有简单的解.但是当把n连续化并求趋向于0的极限时，这个模型不能继续下去.

1975年，谢林顿(D. Sherrington)和柯克帕特里克(S. Kirkpatrick)提出了自旋玻璃的平均场理论模型，即谢林顿-柯克帕特里克模型[23]. 他们指出，在爱德华兹-安德森模型的基础上，如果把相互作用长度改为无穷远，以致于所有格点间的相互作用常量的P(Jik)对于任意1对格点都相等，这时平均场得到的解是精确解.该模型与爱德华兹-安德森模型一样，在把副本方法中的n变为连续实数时遇到了困难，这时序参量qαβ是无穷维的矩阵，其中α,β为副本的指标，0≤α,β≤n，并且是连续实数.通过做出副本对称假设来解决该问题，即序参量qαβ=q，其中α≠β.该模型在某些方面定性地符合自旋玻璃的实验，例如磁化率在Tf处出现的尖端等. 然而该模型表现出许多问题：在TTf时，能量图景中只有1个热力学意义上极大概率的谷；而在T

图12 自旋玻璃的自由能随相空间坐标的变化[20]

3.3.4 副本对称性破缺与帕里西解

帕里西也意识到能量图景的多谷状态和温度降低时体系所发生的副本对称性破缺的问题，并从序参量入手来改进谢林顿-柯克帕特里克模型，通过一系列工作最终得到谢林顿-柯克帕特里克模型的精确解[24]. 重新定义序参量来反映能量图景中的多谷性质，如下

(9)

其中α,β为副本的指标，并且0≤α,β≤n，所以qαβ是无穷维度的矩阵.qαβ的对角元给出了某个副本的重叠程度，非对角元度量了α和β副本的相似程度.

帕里西解说明：在T

4 结束语

玻璃态材料作为一类典型的复杂系统，其研究领域既古老又活跃，安德森认为“理解玻璃以及玻璃化转变的物理本质是极为困难的，这是固体理论中最高深、最有趣的待解决问题”[25]. 而气候变化与人类生存息息相关. 霍金(S. Hawking)在给毕业生的建议中提到21世纪是复杂系统的时代. 美国科学史家、科学哲学家库恩(T. Kuhn)指出某学科成熟的标志是建立科学范式，而复杂系统的研究仍在快速发展中，至今没有与之相适应的范式，缺乏完备的理论基础. 2021年的3位诺贝尔物理学奖获得者为人们从微观到整体理解复杂系统的物理机制做出了开创性贡献，也激励了广大科研工作者继续探索神秘而有趣的复杂系统.