阳光透过鱼缸在室内墙上投射出米级亮丽彩虹

刘新军

(天津大学 理学院 物理系，天津 300350)

1666年初，英国科学家牛顿在暗房间的窗板上开了个小孔，让太阳光进入房内，然后将三棱镜放在光的入口处试验光的颜色[1]. 太阳光从窗板上的小孔入射，经三棱镜折射到墙上，形成了鲜艳明亮的彩色光谱. 该实验奠定了光色散的理论基础，开创了光谱学研究的先端.

2021年3月23日，坐标天津，中午12：30，笔者在室内墙上观察到大片彩虹(面积约为36 cm×1 m)，如图1所示. 经查找，发现彩虹是由阳台窗外支架上鱼缸里的水折射太阳光得到的. 由于鱼缸底部可以看成平面镜，水和平面镜构成水三棱镜，通过折射太阳光形成了彩虹.

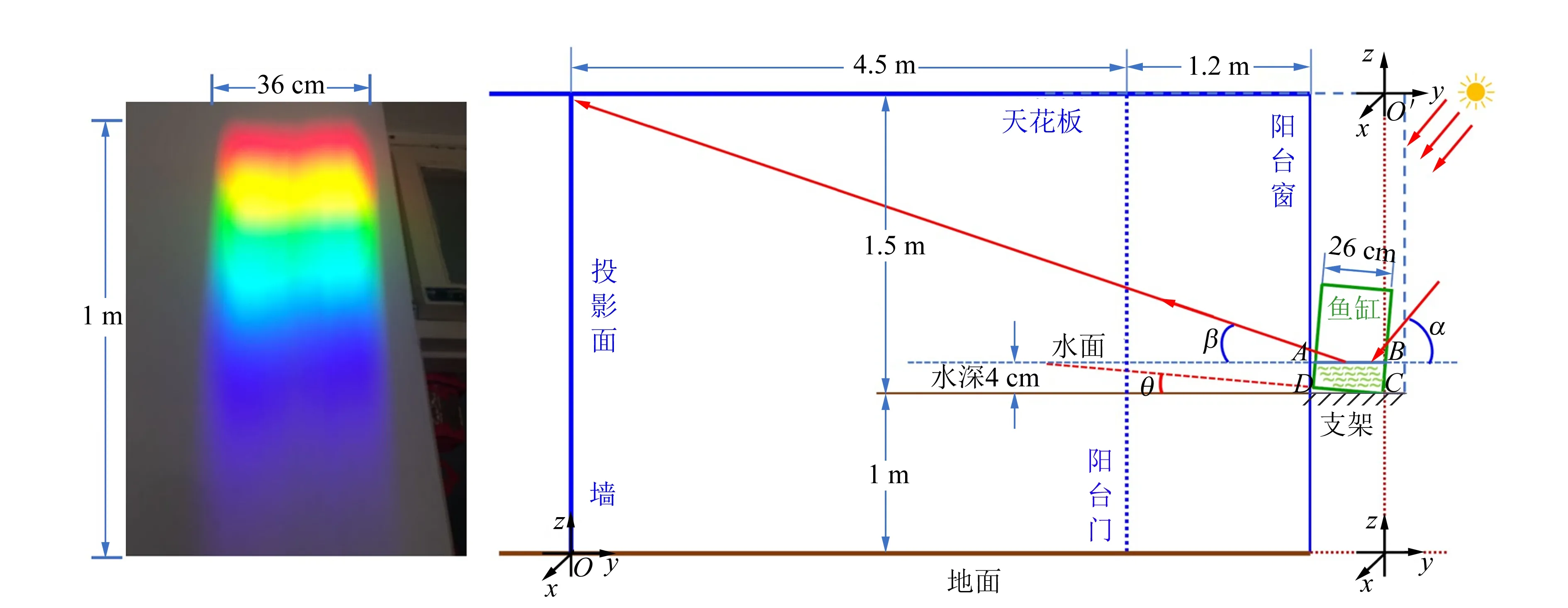
图1 墙上的彩虹以及房间、阳台窗外支架上的鱼缸等相对位置示意图

在通常的水三棱镜实验中，投影面在镜面法向和太阳直射方向的同侧，而以上现象中的投影面在镜面法向和太阳直射方向的异侧. 因此，通常的水三棱镜光路不能解释以上现象，通过计算机模拟白光从鱼缸水面入射也不能获得如此大面积的彩虹. 为此，本文采用鱼缸作为观测装置，多次改变实验参量，结合计算机模拟分析了鱼缸中2种不同光路引起的色散现象，并对其光谱特点进行解析，获得了墙上彩虹来源的等效光路图.

1 阳光色散现象描述

与彩虹相关的场景参量如图1所示. 矩形玻璃鱼缸(37.5 cm×26.0 cm×37.5 cm)底部有约4.0 cm深的清水，鱼缸长边平行于阳台窗户，且垂直于太阳入射光线. 支架距离室内地面的垂直高度约1 m，由于支架上多个垫板的厚度不均匀导致鱼缸向外倾斜，由垫板厚度和鱼缸宽度可以估算出鱼缸底面倾角θ≈5°. 阳台窗户朝向为南偏西20°. 此时，天津地区的正午太阳高度角α≈51°[2]，因此阳光在水面的入射角i1≈40°. 阳台宽1.2 m，房间长4.5 m，鱼缸离墙面的距离L≈5.7 m，墙高2.5 m，边缘红光接近天花板，根据几何关系，可得从水面出射的红光与水面的夹角β=14.85°，因此红光的出射角i5≈75°. 鱼缸底部玻璃外面贴附有黑色软皮胶垫，在强太阳光照射下，鱼缸底部玻璃可以看作是平面镜.

太阳光从空气进入水中，照射到镜面(鱼缸底部)上，经镜面反射后，再从水中向空气中折射，形成彩虹. 该实验获得的彩虹有如下特点：a.呈上红下紫分布，色彩分明，颜色亮丽;b.面积大，约为36 cm×1 m，其横向宽度由鱼缸长边决定，纵向宽度由鱼缸底面倾角θ及墙与鱼缸的距离L决定;c.当太阳方位角改变，观察到彩虹沿垂直墙面向里(x轴的负方向，见图1)的方向移动.

2 阳光色散现象分析

2.1 通常的水三棱镜光路分析(投影面在太阳直射方向的同侧)

阳光充足的日子，在室外准备1盆清水，将镜子倾斜插入盛水的盆中，即可观察到彩虹，如图2所示. 镜面法向在太阳直射方向的同侧,图2(c)为水三棱镜的等效光路图. 主截面内光线1通过水面，折射为光线2，光线2入射到镜面，经反射后为光线3，光线3通过水面进入空气变为折射光线4，即1→2→3→4. 图2(c)中镜面和水面的夹角φ=38°，太阳入射角i1=40°. 根据可见光波长与折射率之间的对应关系[3]，红光(760 nm)和紫光(400 nm)在水中的折射率n分别为1.329和1.343. 因此,在图2(c)中，边缘的红光和紫光的出射角i5分别为77.70°和81.37°.

由镜像对称可知，镜子里面有虚水面，虚光线从虚水面入射到镜子背面，从镜子背面反射后，入射到虚水面，再经虚水面折射后出射，即5→6→7→8. 水面和虚水面之间构成顶角为2φ的三棱镜，其主截面为图2(c)中的绿色三角形. 光线从虚水面入射到水三棱镜后，再从水面出射，即5→6→3→4. 水三棱镜和三棱镜类似，均能使白光产生色散[4].

尽管图1～2中观察到的彩虹均呈上红下紫分布，但图2中的投影面和太阳直射方向在同侧，而图1中的投影面和太阳直射方向在异侧，因此图2不是图1的等效光路. 图1的光路还需要就实验场景特点进行详细分析.

(a) 实物图 (b) A4纸上的彩虹

2.2 阳光从鱼缸水面入射的光路分析(投影面在太阳直射方向的异侧)

鱼缸玻璃壁相当于平行平板，光的传播方向不变，则光线与水面的夹角不变，因此不考虑玻璃对光线传播方向的影响[5].

阳光从AB面射入水中，经镜面DE反射到AB后在AF′区间出射，忽略玻璃缸壁折射的影响，其光路如图3所示.鱼缸底部CD相当于平面镜，倾角θ=5°，水面与支架平面平行，因此CD与AB的夹角也为5°. 图3中水三棱镜的主截面为△BMN，虚水面为MN，其顶角∠BMN=2θ=10°. 利用2.1中的分析方法，阳光将从MN面入射，从AB面出射，其投影面在太阳直射方向的异侧，满足图1中的情况，但仍需对其光路进行仔细分析，以判断图3是否为图1的等效光路.

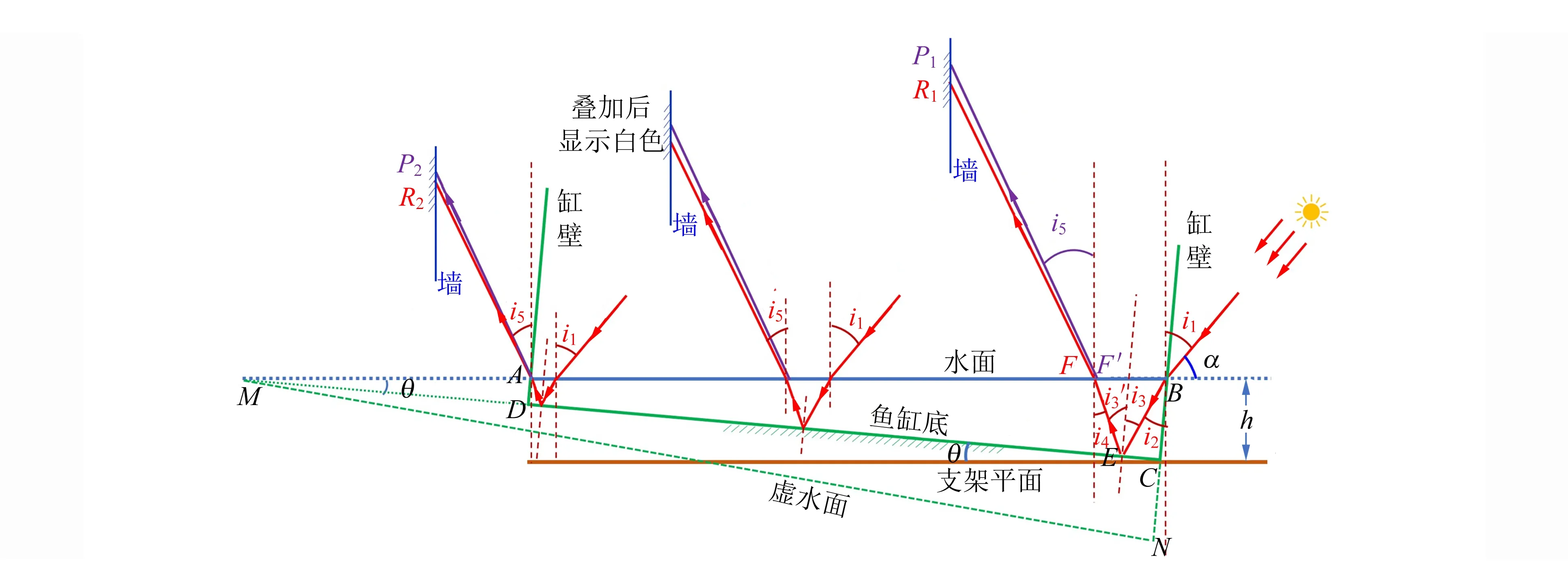
图3 阳光从水面AB入射，再从水面AB出射的光路图

阳光从AB面入射，入射角i1=40°，红光折射角i2=28.93°，i3=i3′=23.93°，则i4=18.93°，红光出射角i5=25.54°(该出射角明显小于75°，说明图3不是图1的等效光路).根据几何关系，得到5个角的关系为：

(1)

2.2.1 红色最高点R1的分析

红光从B点入射，F点出射，则两点之间的距离为

(2)

由于鱼缸底面倾斜，各处水深不同，为便于计算，定义最大水深h为C点到水面AB的垂直距离，并假设h=4.0 cm，则BF=3.45 cm.该红光投影到室内墙上的位置为R1，假设墙与地面的交点为O(见图1)，且O点为竖直方向坐标零点的位置，则R1距离地面的高度为

OR1=d+h+[L+CD(1-cosθ)+

(3)

其中,d=100 cm为阳台窗外支架平面到室内地面的垂直高度，h=4.0 cm为最大水深，CD=26 cm为鱼缸底面宽度，L=570 cm为墙(或投影面)与鱼缸的距离.将已知参量代入式(3),可计算得到红色最高点位置OR1=1 346 cm，该数值远大于墙高250 cm，与图1中彩虹上边缘红光的位置不符.

2.2.2 紫色最高点P1的分析

利用式(1)求出紫光出射角i5=25.36°，比红光出射角小.从水面最右端B点入射的紫光，其出水点为F′，利用式(1)和式(2)可以求得BF′=3.40 cm，与红光出射点F(见图3)相差0.5 mm.该紫光投影到室内墙上的位置为P1，将式(3)中的BF替换成BF′，即可求出紫色最高点位置OP1=1 356 cm>OR1，说明紫光在红光之上，从紫到红的颜色变化宽度为OP1-OR1=10 cm，故彩虹从上到下的顺序为紫蓝青绿黄橙红(上紫下红)，与图1中观察到的现象不同.

2.2.3 红色最低点R2的分析

2.2.4 紫色最低点P2的分析

A点出射的紫光在墙上的投影位置为P2，利用式(1)和式(3)，将BF替换成BA，即可求出紫色最低点位置OP2=1 308 cm>OR2，说明紫光在红光之上，紫光到红光的变化宽度为OP2-OR2=10 cm.

2.2.5 彩虹特征

根据以上分析，彩虹中间范围内(R1P2=OR1-OP2=38 cm)由所有颜色的光叠加而成,形成白光,而彩虹纵向宽度w=OP1-OR2=58 cm，故两边分别为10 cm的彩边.因此，图3显现出的彩虹特征为上紫下红，中间白两边彩，与图1的实验现象完全不符，故图3不是图1的等效光路.

2.2.6 计算机模拟

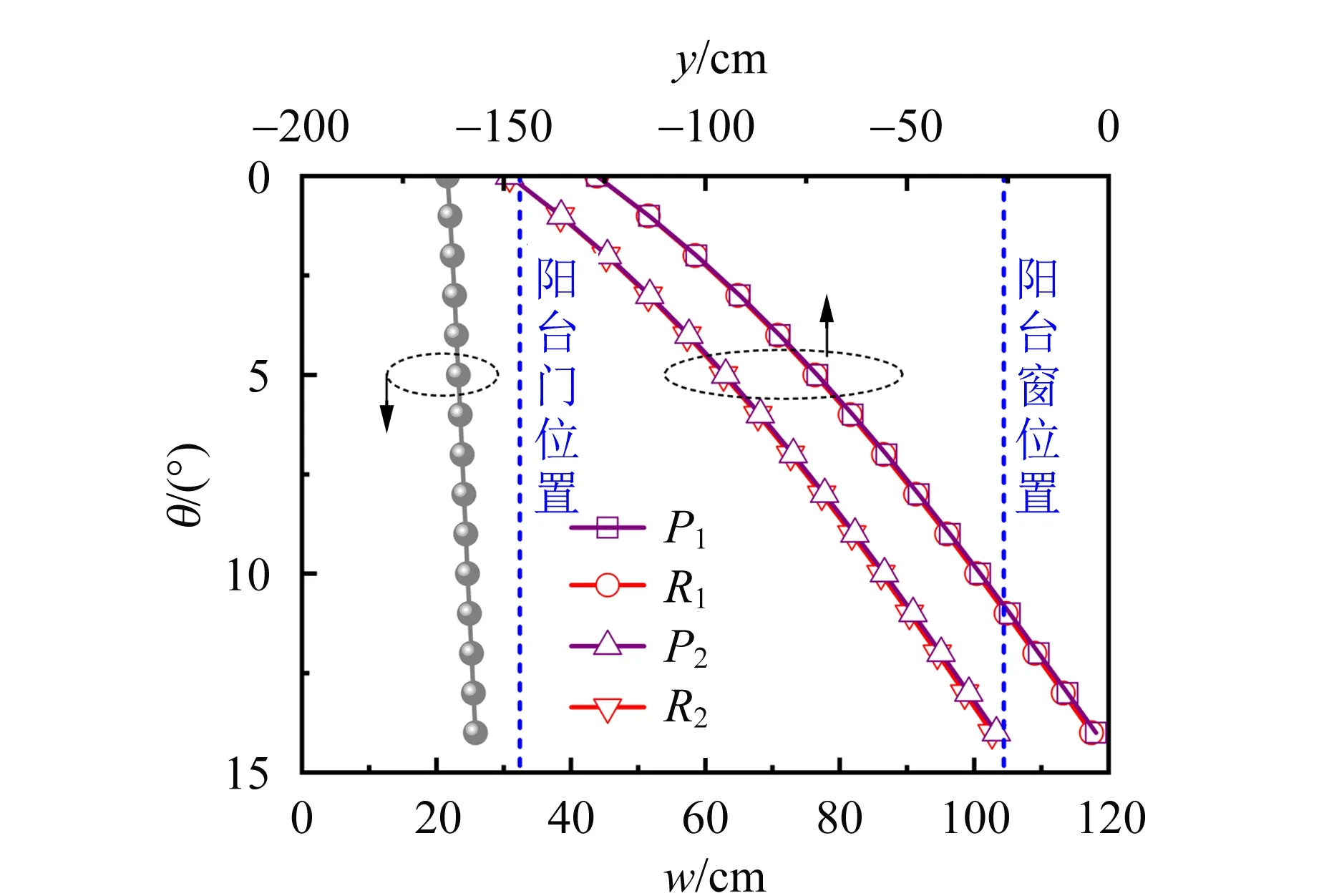
以鱼缸底部C点为支点，通过垫高底部左端D点可以连续调节鱼缸底面倾角θ.当阳光从AB面入射时，入射角i1=40°,h=4.0 cm,θ=1°～14°时，计算出红(紫)光在墙上的投影位置z以及相应彩虹的纵向宽度w，部分模拟结果如图4所示.

图4 红(紫)光在墙上的投影位置z和彩虹纵向宽度w随鱼缸底面倾角θ的变化关系1

当θ=8°时，w=106 cm，与图1中彩虹纵向宽度相当，但彩虹特征仍为中间白两边彩(中间为45 cm的白色，两边为31 cm的彩边)，且红(紫)光的投影位置在20 m附近，再次表明图3不是图1的等效光路图.

2.3 阳光从鱼缸侧水面入射的光路分析(投影面在太阳直射方向的异侧)

由2.2的光路分析和计算模拟可知，阳光从AB面入射时，彩虹的投影面在太阳直射方向的异侧，符合图1的实际情况，但彩虹特征和投影位置与图1情况不符.

经过反复实验，发现墙上彩虹可能来源于鱼缸BC面上入射的阳光,忽略玻璃缸壁折射的影响，其光路如图5所示.阳光从BC面入射，经鱼缸底部EC面反射后，在F′G面出射.鱼缸底部CD相当于平面镜，BC面的镜像为虚水面NC.阳光从BC面入射可等价于阳光从虚水面NC入射，经过水三棱镜△MBN，再从AB面出射.

图5和图3中水三棱镜的主截面相同，但图5中水三棱镜的顶角为∠MBN=90°-θ=85°.另外，图3中AB面上入射光的垂直宽度约为20 cm，图5中BC面上入射光的垂直宽度仅约为2.3 cm. 此外，图5的投影面在太阳直射方向的异侧，与图1中观察到的情况一致，下面将对图5所示的光路进行分析.

根据几何关系，阳光从BC面入射的入射角i1=55°，红光折射角i2=38.06°，镜面入射点为E，入射角i3和反射角i3′为51.95°，从水里入射到空气中的入射角i4=46.95°，红光在空气中的折射角，即红光的出射角i5=76.21°(该出射角接近图1中估计的75°，初步说明图5可能是图1的等效光路).这5个角的关系为 :

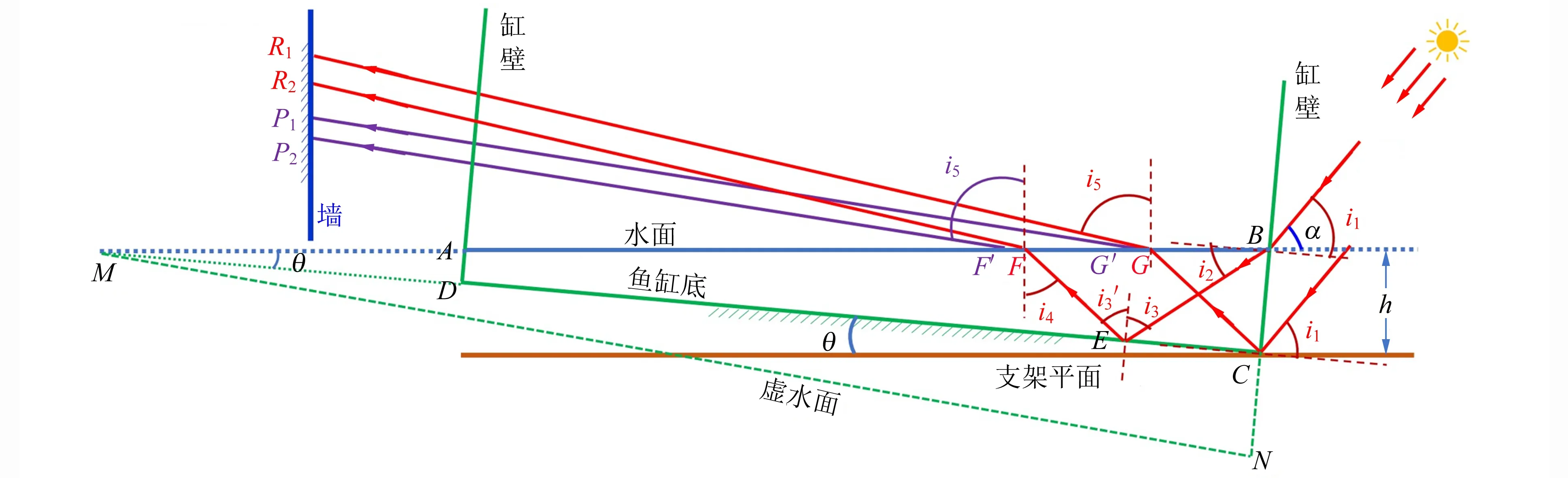
图5 阳光从侧水面BC入射鱼缸，再从水面AB出射的光路图

(4)

2.3.1 红色最低点R2的分析

红光从B点入射，从F点出射，两点之间的距离为

(5)

计算可得BF=9.27 cm.红光投影到室内墙上的位置为R2，墙与地面的交点为O，利用式(3)可得红色最低点位置OR2=248.15 cm，该数值小于墙高250 cm，故能够在墙上观察到红光.

2.3.2 紫色最低点P2的分析

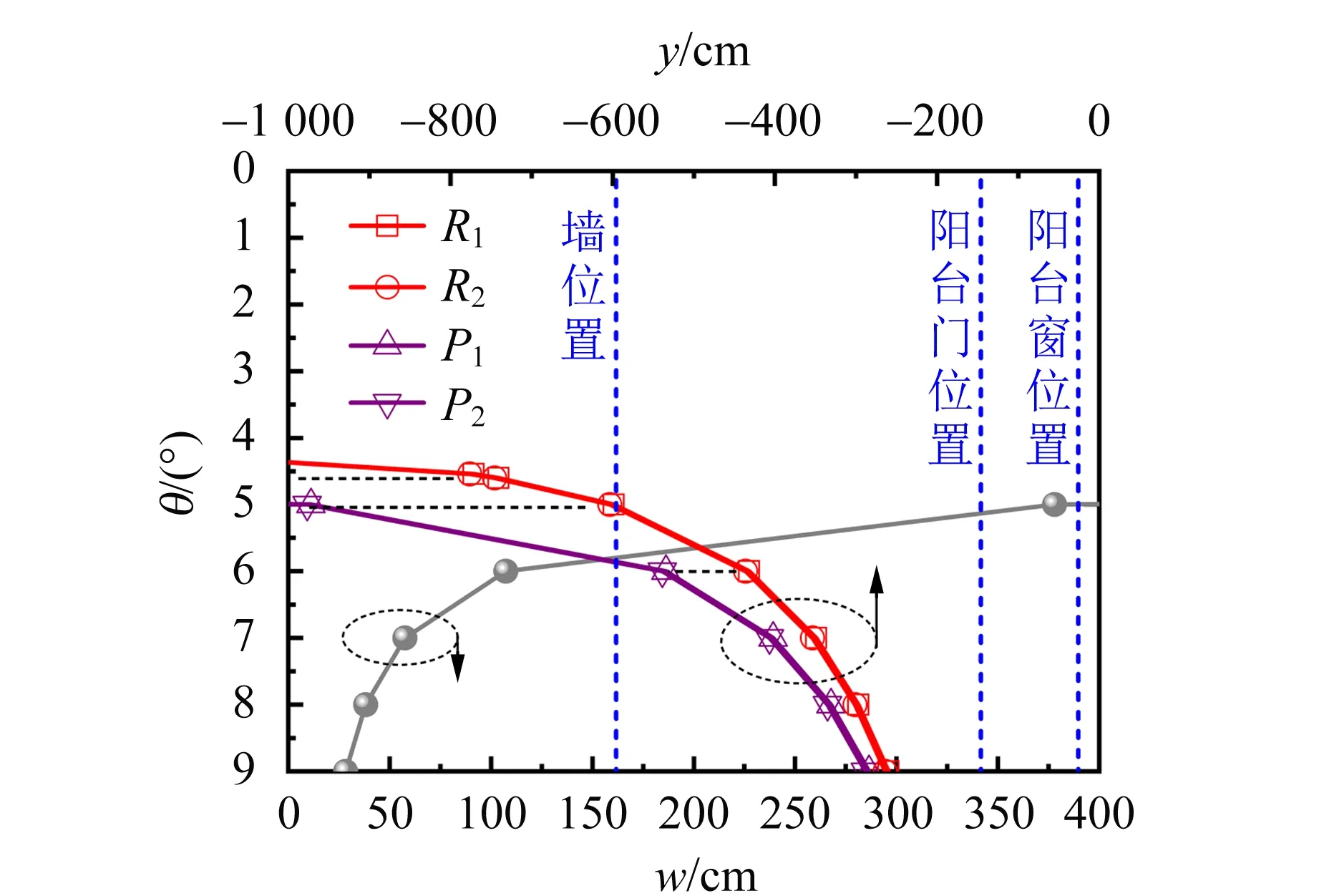
利用式(4)求出紫光出射角i5=81.43°，比红光出射角大.从B点入射的紫光，其出水点为F′，利用式(4)～(5)得到BF′=9.41 cm>BF，说明紫光出射点F′在红光出射点F的左侧(见图5)，且FF′=1.4 mm.紫光投影到墙上的最低位置为P2，将式(3)中的BF替换成BF′，即可求出紫色最低点位置OP2=192.55 cm

2.3.3 红色最高点R1的分析

由于整个BC面都有入射光线，水面最下端C点入射的红光经镜面反射后在G点出射，故B点和G点之间的距离为

BG=h[tanθ+tan (i3-θ)] ，

(6)

计算可得BG=4.64 cm.G点出射的红光投影到墙上的位置为R1，将式(3)中的BF替换成BG，可得红色最高点位置OR1=249.29 cm，该数值小于墙高250 cm，与图1彩虹的上边缘红光位置一致.

2.3.4 紫色最高点P1的分析

侧水面最下端C点入射的紫光在G′点出射，利用式(4)和式(6)可以求出BG′=4.70 cm，在红光出射点G的左侧(图5)，二者仅相差0.6 mm.G′点出射的紫光投影到室内墙上的位置为P1，将式(3)中的BF替换成BG′，可求出紫色最高点位置OP1=193.26 cm

2.3.5 彩虹特征

红光投影的最高点位置R1和最低点位置R2之间相差OR1-OR2=1.14 cm，紫光投影的最高点位置P1和最低点位置P2之间相差OP1-OP2=0.71 cm.由于整个BC面都有阳光入射，故墙上R1到P2范围内颜色都是叠加而成的，且在R2到P1范围内重叠更多，但重合区域处几乎都是单色光叠加(Δλ<7.33 nm)，故整体彩带的纵向宽度w=OR1-OP2=56.74 cm，颜色呈上红下紫分布，与图1现象一致.虽然该彩虹的纵向宽度只有图1中的3/5，但通过减小鱼缸底面倾角θ或入射角i1可以获得与图1相同的彩虹纵向宽度，故图5的光路是图1的等效光路.

2.3.6 计算机模拟

以鱼缸底部C为支点，调节底部左端D点位置可以连续改变鱼缸底部倾角θ.当阳光从BC面入射的角度i1= 55°,h=4.0 cm,θ=1°～40°时，计算得到红(紫)光在墙上的投影位置z和相应的彩虹纵向宽度w，部分模拟结果如图6所示.

图6 红(紫)光在墙上的投影位置z和彩虹纵向宽度w随鱼缸底面倾角θ的变化关系2

当θ=4.54°时，红光的出射角为79.23°，而紫光的出射角为89.64°，刚好从水面水平出射. 此时，在墙上高于水面的位置刚好可以观察到全部颜色的彩虹，彩虹的纵向宽度为108.86 cm(Δλ<2.97 nm)，略大于图1中彩虹的纵向宽度.

当θ<4.54°时，紫光在出射点发生全反射，即i4>48.13°(紫光的全反射角)，故紫光不能出射到空气中，因此只能观察到部分颜色的彩虹.

当θ≤4.02°时，红光在出射点处发生全反射，即i4>48.81°(红光全反射角)，故红光不能出射到空气中.在不考虑光线在水面和镜面之间多次反射的情况下，在墙上观察不到彩虹.

由于计算中假定最大水深h=4.0 cm不变，故当θ>8.85°时，水面宽度开始减小.从BC面入射的阳光在水面F′G区间出射(当θ=5°时，F′G=BF′-BG=4.77 cm)，且BF′随θ增大而减小.经计算，直到θ=40°时，水面的宽度仍能满足光线的出射要求，所以出射彩虹的纵向宽度w在此期间不受θ的影响.此外，当θ>40°时，出射光线或投影面，在太阳直射方向的同侧，与图1情况不符，不予考虑.需要注意的是，在水量不变的情况下，水深随着鱼缸底面倾角略有变化，但此计算结果仍然适用.

3 拓展讨论

3.1 天花板上的彩虹

2.2和2.3的分析只给出了墙上彩虹投影位置的分析过程，事实上天花板也可以看作投影面.室内墙的高度有限，所以彩虹在墙上的投影位置不能太高.当投影位置超过墙高时，彩虹就到了天花板上.图7所示为阳光从水面AB入射时，彩虹在天花板上的投影位置y和彩虹纵向宽度w随鱼缸底面倾角θ的变化关系.

图7 红(紫)光在天花板上的投影位置y和彩虹纵向宽度w随鱼缸底面倾角θ的变化关系1

以鱼缸底部C为支点，垫高D点增大鱼缸底面倾角θ的过程中，C点位置不变.由C点向天花板作垂线，其垂足O′点作为天花板上水平方向的坐标零点位置(见图1)，位于阳台窗外支架的顶部，往左依次为阳台、房间和客厅.因此，阳台窗的位置为-26 cm，阳台门的位置为-146 cm，房间和客厅之间的墙的位置为-596 cm，见图7和图8中的蓝色竖虚线.

在入射角i1=40°不变的情况下，彩虹纵向宽度w主要取决于水面宽度AB.经计算可知，当θ=5°时，天花板上的彩虹中间有22.11 cm的白色区域，两边各有约0.6 cm彩带，此彩虹特点为中间宽白、两边窄彩.事实上，由于彩虹位置在阳台顶上，背景光太亮，因此边缘彩带很难分辨.连续增大θ，其彩虹投影位置向阳台窗户方向移动(水平向右，即图1中y轴的正方向)，彩虹纵向宽度略微增加，如图7所示.

相比之下，在室内有限空间中，阳光从鱼缸侧水面BC入射可以在房间的天花板上观察到纵向更宽的彩虹.图8为阳光从BC面入射时，彩虹在天花板上的投影位置y和彩虹纵向宽度w随鱼缸底面倾角θ的变化关系.当θ=5°时，天花板上的彩虹纵向宽度w=3.78 m(Δλ<4.53 nm)，但由于墙高的限制，彩虹呈现在墙上.当θ=6°时，天花板上的彩虹纵向宽度w=1.08 m.当θ=7°，8°时，彩虹纵向宽度w分别为57.47 cm和38.16 cm.当θ=39°时，w=5.90 cm，投影位置为阳台窗外的支架顶.即w随θ的增大而减小.

图8 红(紫)光在天花板上的投影位置y和彩虹纵向宽度w随鱼缸底面倾角θ的变化关系2

3.2 不同季节的彩虹

春分或秋分前后，天津地区正午太阳的高度角α≈50°[2]，当鱼缸底面倾角θ=5°时，在距离鱼缸5.7 m远的墙上能观察到颜色分明的彩虹.夏至和冬至，天津地区正午的高度角α分别为74°和27°[2]，如果仍保持θ=5°不变，在距离鱼缸5.7 m远的墙上还能观察到彩虹吗？

假设θ=5°不变，通过计算机模拟阳光从BC侧水面入射鱼缸的情况，如图9所示.通过分析发现只有在春分和秋分前后，太阳高度角α=48.7°～51°时，才能在墙面上观察到大片彩虹.

图9 红(紫)光在墙上的投影位置z和彩虹纵向宽度w随正午太阳高度角α的变化关系

3.3 1天内不同时刻的彩虹

以上关于彩虹的讨论，满足鱼缸长边垂直于太阳入射光线，且平行于投影面(墙).当鱼缸位置不变时，随着时间的推移，太阳的高度角和方位角都发生变化，彩虹的投影位置会沿x轴负方向移动.当想在晴天任意时刻都能通过鱼缸观察到彩虹时，可以根据太阳的高度角和方位角，调整鱼缸底面倾角以及投影面(可以选择移动的画板)位置来实现.

2021年4月18日早上9：50，迎着阳光调整鱼缸底面倾角θ，将彩虹(上红下紫)投影在阳台上晾晒的衣服上，如图10(a)所示.此时CD面(鱼缸底面)的法线方向在太阳直射方向同侧，而阳光从鱼缸BC面入射，投影面在太阳直射方向异侧，与图5情况一致.继续调整θ，使CD面的法线方向在太阳直射方向异侧，观察到了中间白、两边彩(上紫下红)的彩虹，此时阳光是从AB面入射，且投影面在太阳直射方向异侧，如图10(b)所示.

(a) 上红下紫 (b) 中间白、两边彩图10 鱼缸位置和衣服上的彩虹

当太阳方位发生变化，但仍想通过调整鱼缸观察到彩虹，就须沿底面对角线适当倾斜鱼缸，并且其长边不垂直于入射太阳光. 通过反复调整角度，玻璃缸壁上会出现2道彩虹，如图11所示. 其原因是太阳光从两侧水面射入水中，各自经缸底反射后，再从水面出射形成色散造成的.

图11 鱼缸缸壁上的2道彩虹

4 结束语

本文从室内墙上观察到大片彩虹现象入手，利用几何光学研究了阳光从矩形玻璃鱼缸水面和侧水面入射的2种不同光路引起的色散现象，以及各自的光谱特点和产生原因，同时利用计算机进行模拟，所得结果与实验现象一致. 阳光从矩形玻璃鱼缸侧水面入射，由于鱼缸底面倾角具有易操控性和连续可变性的特点，因此丰富了水三棱镜实验的现象. 另外，该实验所需器材简单、操作方便，不仅有利于居家演示和科普宣传，还有利于在教学和科普中的应用和拓展，为青少年对光谱及色散现象的了解和认知提供了实验基础.