基于宏观基本图的禁左交通组织评价模型

李冰，杨鸿宇，郑佐雄，冯悦，王正辉

(1.昆明理工大学，交通工程学院，昆明 650500；2.云南工程勘察设计院集团有限公司，昆明 650224)

0 引言

随着车辆保有率的持续增加，交叉口过饱和交通状态已逐渐呈现常态化，对于大城市而言，过饱和交通状态已从交叉口过饱和演化为区域性过饱和。不少城市在面对巨大的交通压力时，通常会通过完善道路渠化和优化信号配时等交通组织措施来缓解交通压力，对交叉口实施禁止左转(禁左)是一种有效地缓解交通压力的交通组织手段。在对交叉口禁左分析时，吴伟等[1]综合考虑禁左绕行范围、流量守恒、绿灯时间、饱和度及周期时长等约束条件，建立干线禁左的混合整数线性规划模型；阿拉腾[2]构建了基于模糊综合评价方法的禁止左转评价体系模型。现有禁左研究在单点禁左评价时多以考虑邻近交叉口的影响为主，或者仅分析干道上的交叉口禁左，难以从区域宏观层面系统评价禁左交通。例如，昆明市自2005年以来，陆续对主城区一环内几乎所有信号交叉口采取禁左交通组织，2020年9月又对所有路口取消禁左管控，然而，这一区域禁左与取消禁左均缺乏较为科学全面的理论分析，部分出行者不能很好地适应这一措施带来的出行变化，所以，如何科学评价区域禁左具有重要的现实意义。

为从宏观层面系统刻画城市交通运行状态，研究人员从20世纪70年代开始使用宏观基本图的概念对城市路网进行建模，MFD 最初观点由GODFREY[3]在1969年提出，它是路网的固有属性，是区域交通流量、密度及速度间的关系或车辆总运行距离和运行时间的关系；2007年，DAGANZO[4]从理论上证明了MFD 的存在；2008年，GEROLIMINIS 等[5]首次以横滨的大量实测数据，有力地刻画了MFD的形状，从路网整体结构出发，完善了利用MFD形式量化描述道路或路网内宏观交通流参数之间关系的模型和方法，并进一步阐述了MFD与城市交通流构成和路网管控措施等因素的内在联系；许菲菲等[6]的研究同样表明，交通需求的剧烈变化和车道禁行等都会不同程度影响路网MFD；LUKAS 等[7]提出了一种物理意义的宏观基本图函数形式，并进一步增加了MFD 的实用范围。如何利用MFD对城市交通运行进行有效评价与管控已成为研究的热点，也为区域型交叉口禁左评价提供了理论依据。在现有MFD的实际运用研究中，大部分集中在交通状态判别和信号控制方面。惠彦彦等[8]提出引用MFD 作为交通控制决策的评判手段，建立并分析MFD 形态与交通控制参数(信号周期和相位差)的量变关系，以支撑信号控制决策，也为禁左影响下的MFD构建提供了思路；LU等[9]基于MFD概念，提出最大通过量、临界累积量、网格累积量和同质度这4个评价指标评价区域信号控制方案在道路网络中的有效性，研究成果为本文不同禁左范围影响下的MFD交通状态评价提供了理论依据；GUO 等[10]用MFD 描述每个区域的动态特性，用点排队模型描述在边界处形成的排队动态特性，并利用瞬时动态用户平衡原理对出行者的路径选择行为进行建模，该思路也为本文禁左后的MFD分析提供了理论支撑。

综上可知，基于MFD 的网络交通运行状态表征优势，为交通管理者从宏观层面分析交叉口禁左前后的交通状态提供了理论支撑，如何将MFD 与禁左后交通流量转移机理相结合是刻画禁左MFD的关键。因此，本文首先根据概率模型分析禁左交通流量转移机理；其次，建立不同左转车流比例和不同禁左范围下的MFD 禁左评价模型，得出禁左后的最佳交通运行状态；最后，通过VISSIM仿真验证分析模型，为禁左措施的科学组织提供设计依据。

1 禁左流量转移分析

交叉口禁左是交通管控中经常采用的措施，在交叉口禁左后，原有的左转车流会通过提前左转、延后左转及右转绕行这3种方式完成左转，而不同转移路径概率模型的精确构建是分析禁左措施是否可行的关键，本文借鉴WU等[11]的研究思路分析左转车流禁限后的分流概率。如图1所示，当i路口禁左时，原来的左转交通流有3种选择：

(1)提前左转，交通流可以在十字路口i+1 和i+2 提前左转。

(2)延后左转，车流可以在交叉路口i-1左转。

(3)右转绕行，即在当前的交叉口i先右转，然后掉头。

3 种路径都会带来不同程度的出行延误，本文通过绕行距离区别不同左转方式的延误，然后，在Logit 模型中利用绕行距离完成左转流量的重新分配。

如图1所示，当i≠j时，交叉口i和j的绕行距离为交叉口i到交叉口j的距离(把交叉口i和交叉口j的中心点作为计算距离时的参考点)。如果i=j，则定义dii为其绕行距离为

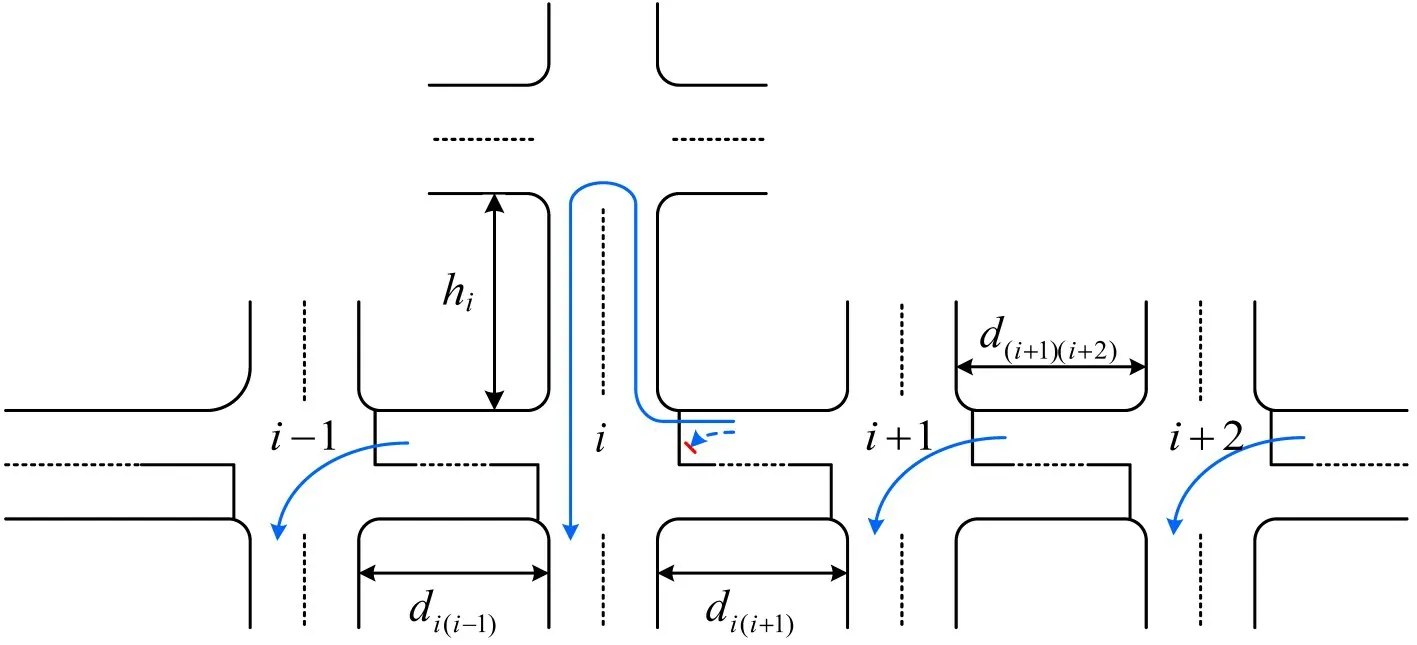
图1 左转流量转移示意Fig.1 Traffic redistribution after left-turn prohibition

式中：hi为i路口车流从右转到掉头经过的距离。

如果交叉口i不允许左转，那么原本在交叉口i左转的车流量qia→d将重新分配到其他交叉口，其中，a 为进口道，d 为左转的出口道。交叉口i流量转移到交叉口j的流量概率为

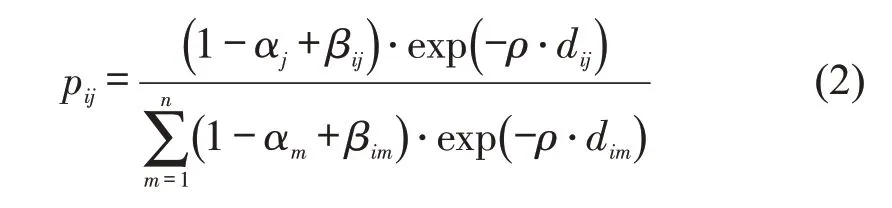
式中：i,j,m∈{1,2,3,…,n}；pij为左转车流分配的概率；ρ为Logit模型中与绕道距离相关的系数；αj为左转禁止决策的二进制变量；βij为辅助参数。i=j和i≠j两种情况同时包含在式(2)中，如果i=j，则βij=1；否则，βij=0。当交叉口i允许左转时，αj=0；否则，αj=1。如果i≠j时，βij=0，此外，如果1-αj+βij=1时，则需要αj=0，pij才为正，即交叉口j允许左转原来i的左转车流才会分配到j；当i=j时，βij=1，因为，在交叉处不允许左转，αi=αj=1，因此，(1-αj+βij)=1(原来i的左转车流要右转绕行)。从式(2)中可以看出，当绕道距离越大时，选择与之相关的出行方案比例越小。

为标定模型，验证路网中路口禁左后的左转车流分配概率，本文根据昆明市实地路网交通数据，结合VISSIM仿真软件模拟，对北京路、人民东路及环城东路这3 条主干路选取关键路口禁左后的绕行车辆进行分析，选取绕行交叉口如图2所示，数据统计示例如表1所示。

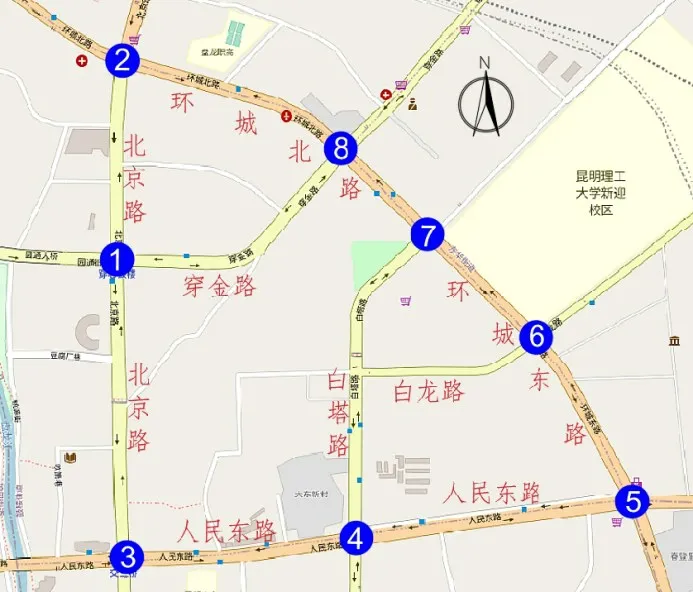
图2 禁左路口示意Fig.2 Schematic diagram of left-turn prohibition of intersections

当绕行方案距离差小于100 m时，出行者对于不同绕行方案的选择比例相同；当绕行方案距离差大于100 m时，每增加100 m的距离差，选择绕行距离大的方案出行者人数就会下降14.5%；当距离差大于1000 m 时，出行者几乎不会选择绕行距离大的方案。上述禁左流量转移分析所得到的左转车流分配概率pij为禁左后MFD 模型的建立提供了理论支撑。

2 禁左交通组织评价模型

2.1 MFD基础理论

MFD反映了路网内车辆数与路网运行水平的关系，即建立路网内的加权流量与路网总交通量(Q)之间的关系。根据MFD理论，以路段长度对车流量进行加权处理，得到MFD加权流量，相关参数计算式为

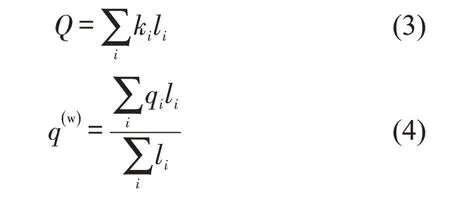
2.2 不同禁左范围交通组织下的MFD模型

为提升所建模型的普适性与可靠性，分别从单点、干道及区域这3类评价范围依次构建禁左MFD评价模型。

2.2.1 单点禁左

为得出单点交叉口最佳的MFD，需充分考虑禁左后的流量转移概率，结合禁左流量转移分析，禁左后的流量转移概率对原始MFD进行流量加权处理可得单点禁左MFD模型为

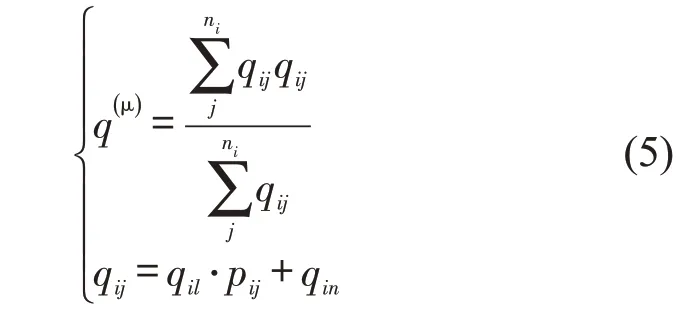
2.2.2 干道禁左

鉴于禁左导致原本左转的车辆变成直行或右转绕行，而MFD 基础理论并未考虑流量转移对于MFD的影响，所以，需要重新构建干道禁左模型绘制干道禁左MFD。由于禁左后的流量转移会对MFD产生影响，所以，综合考虑左转车流分配到其他车道的情况和主干道长度，将MFD 流量加权方式由原来的道路长度加权转变为以路段长度乘以车道数加权，根据流量转移分析，相关计算式为

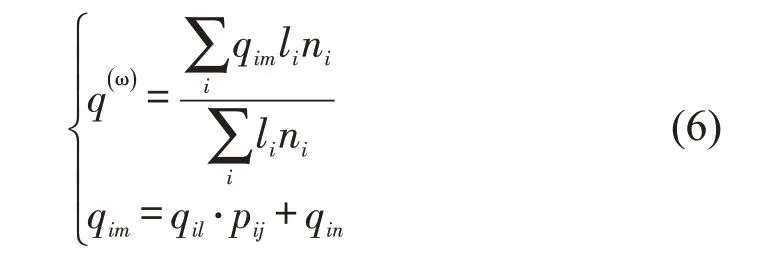
通过VISSIM 仿真发现，不同等级道路禁左对MFD 有不同的影响，主干道与次干道对路网MFD影响较大，支路对MFD 的影响相对较小；为此，本文对同一路网中的不同等级道路进行系数修正。首先，对整体路网进行仿真，得出原始MFD，再分别对主干道、次干道及支路禁左进行仿真，得出不同等级道路的MFD，最后，通过与原始MFD 对比得出式为

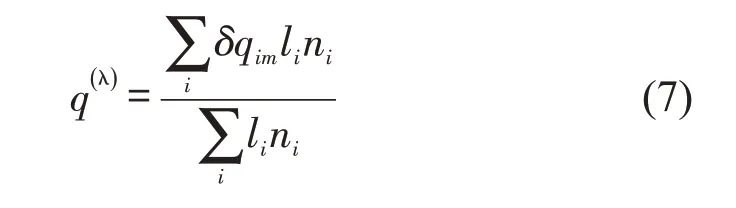
2.2.3 区域禁左

由上述分析可知，单点交叉口禁左与干线交叉口禁左对整个区域的交通状态影响程度不同。在VISSIM绘制MFD时，发现单点禁左与干线禁左的MFD 形状相似，并且根据最小二乘法拟合的一元二次回归方程的峰值点横坐标和对称轴基本一致，表明单点禁左MFD 和干线禁左MFD 的变化存在一定的比例关系，所以，通过比例加权将两者结合构建区域禁左MFD 模型。区域禁左MFD 计算式为

首先，将单点禁左MFD 参数计算与干道禁左MFD 参数计算模型进行加权处理，得出整个路网的MFD 参数计算模型，其中，加权值a、b分别对应干道加权流量与交叉口加权流量；其次，通过VISSIM搭建仿真实验路网得出区域禁左后的原始MFD，再分别结合单点禁左模型和干道禁左模型得出区域MFD；最后，对比原始MFD，求得a=0.78，b=1.21，得出验证环境下区域禁左MFD 模型计算式为

3 模型验证与分析

3.1 仿真环境搭建与分析思路

选取昆明市北京路-环城北路-人民东路所围区域对本文模型进行仿真评价，其中，北京路为交通量最大的双向八车道主干道，人民东路、环城南路及环城北路为车流量次之的双向8车道主干道，白龙路、穿金路及白塔路为次干道。模型仿真评价区域如图3所示。通过数据分析得到未禁左时的MFD，如图4所示。

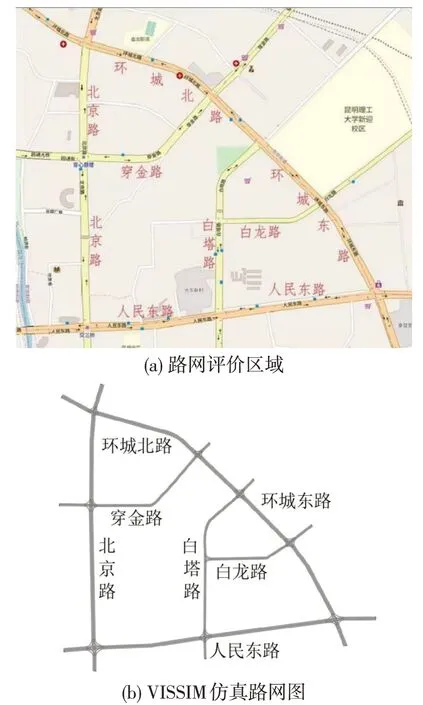
图3 模型仿真评价区域Fig.3 Model simulation evaluation area

其中，最大加权流量点的坐标为(560,2180)，即当车辆累积量到达560 veh 时路网最通畅，加权流量为2180 veh·h-1。数据经最小二乘法拟合后，得到未禁左时的MFD一元二次回归方程为

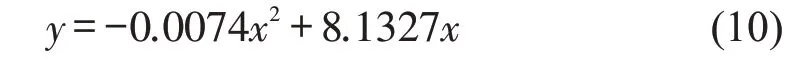
式中：x为路网中的车辆累积量；y为根据模型得出的加权流量。

在图4拟合的一元二次回归方程中，可以将函数按照流量饱和度分为非常通畅饱和度[0～40%]，通畅饱和度(40%～75%]，轻度拥堵饱和度(75%～100%)，以及拥堵饱和度≥100%，通过以上划分能更直观地观察到不同车辆累积量下的交通状况，文中所有MFD皆按此规则划分。

图4 未禁左时的MFDFig.4 MFD of no left-turn prohibition

3.2 不同范围禁左下MFD评价

根据单点禁左、主干道(北京路)禁左及区域禁左绘制MFD，综合分析得出区域内最佳禁左条件。

3.2.1 单点禁左

在实地调查与仿真过程中，北京路与穿金路交叉口(图2中编号①的交叉口)作为本文所选区域主干道中车流量最大的交叉口，左转车流占比适中，且左转车流与直行车流冲突严重，本文对该路口禁左后的MFD进行分析评价。

通过左转车流禁限比例的VISSIM仿真数据拟合，得到北京路与穿金路交叉口禁左后MFD，如图5所示。

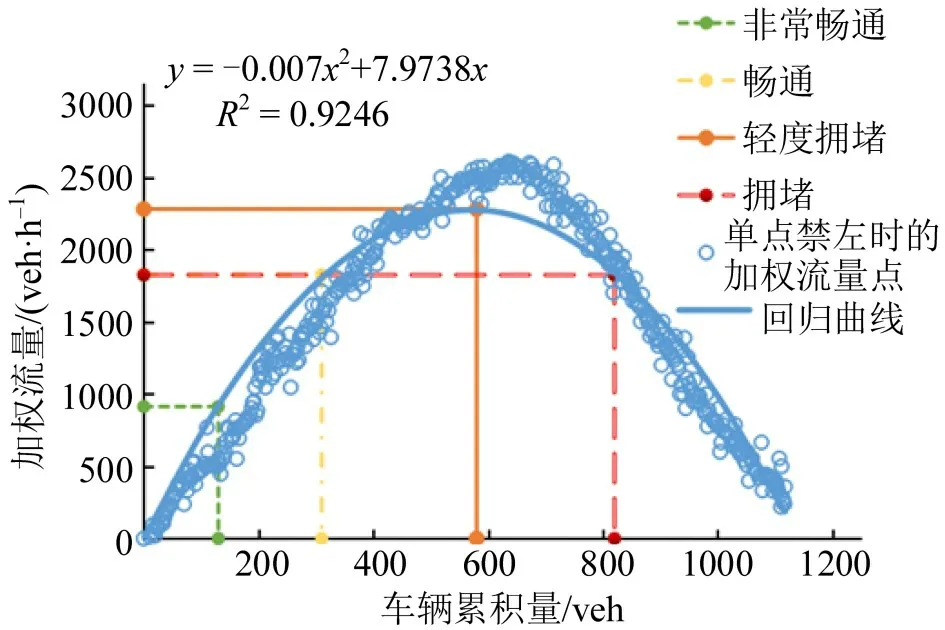
图5 单点交叉口禁左后的MFDFig.5 MFD of left-turn prohibition at single intersection

其中，最大加权流量点为(580,2300)，表明当车辆累积量为580 veh时，路网最通畅，对应加权流量为2300 veh·h-1。北京路禁左后的加权流量相比于未禁左的加权流量增加5.5%。数据经最小二乘法拟合后，得到MFD一元二次回归方程为

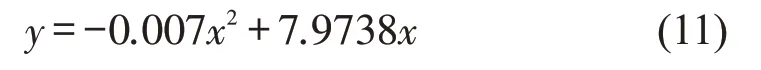
3.2.2 干道禁左

实地调研可知，北京路为双向8 车道主干道，是评价片区内交通压力较大和左转车流占比最大的主干道，包括：北京路与环城北路，北京路与穿金路，北京路与人民东路这3个交叉口；环城北路、人民东路及穿金路为流量较少的主干道，且左转车流少于北京路，所以，对主干道北京路实行禁左(对图2中编号①到③的路口禁左)，通过仿真数据得到其MFD如图6所示。

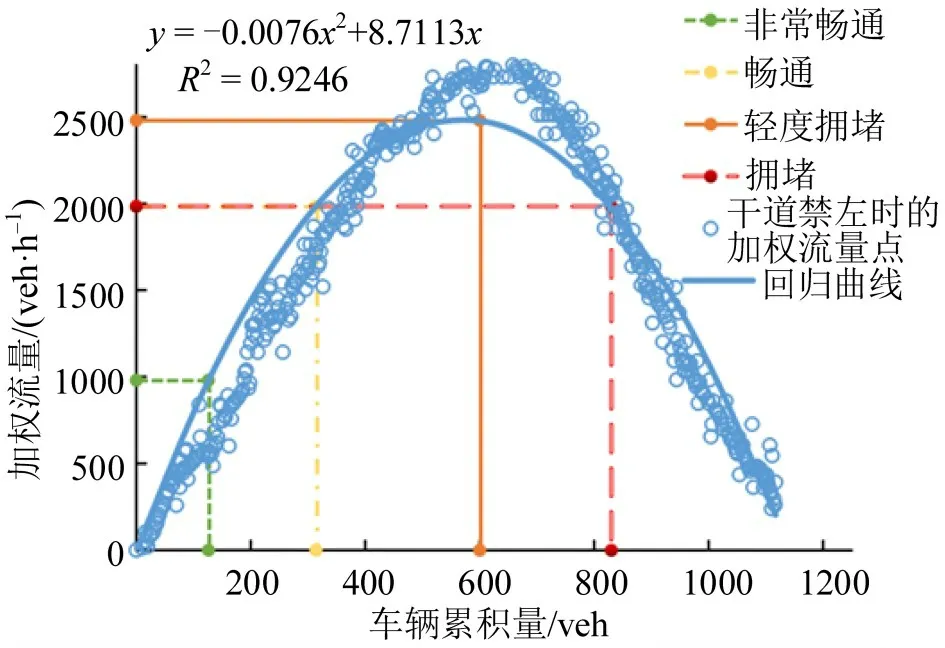
图6 干道交叉口(北京路)禁左后的MFDFig.6 MFD of left-turn prohibition on trunk road intersection(Beijing Road)

最大加权流量点为(600,2480)，即当车辆累积量到达600 veh 时路网最通畅，加权流量为2480 veh·h-1。北京路禁左后的加权流量相比未禁左的加权流量增加了13.8%。数据经最小二乘法拟合后，得到干道禁左MFD一元二次回归方程为

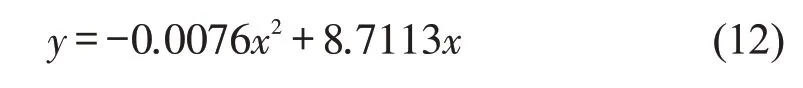
3.2.3 区域禁左

对整个区域实行禁左后(对图2 中编号①到⑧的路口禁左)，可得其MFD如图7所示。

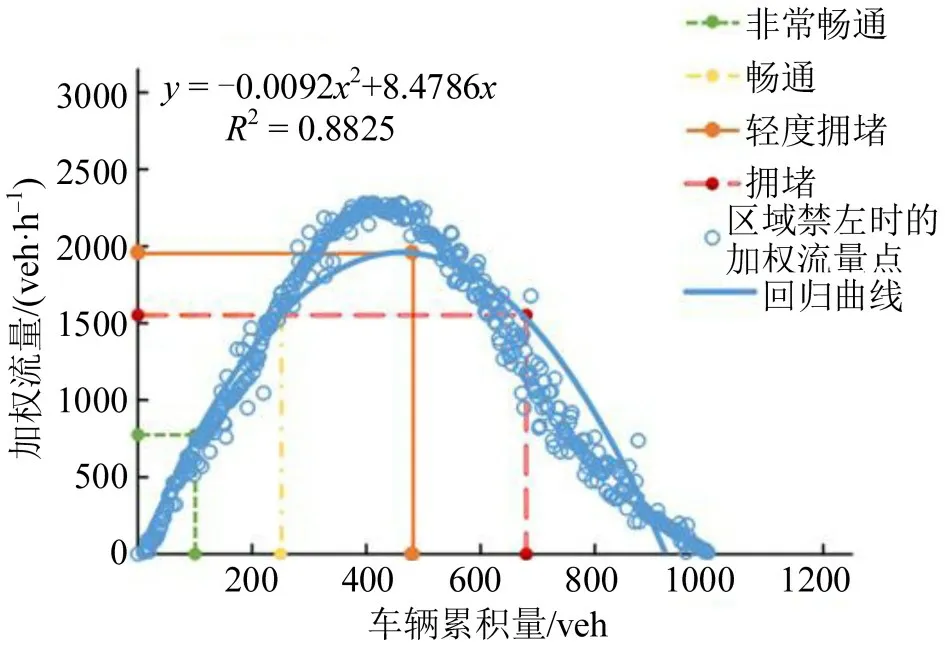
图7 区域禁左后的MFDFig.7 MFD of left-turn prohibition in whole region

其中，最大加权流量点为(460，1960)，即当车辆累积量到达460 veh 前路网最通畅，加权流量为1960 veh·h-1。北京路禁左后的加权流量相比于未禁左的加权流量减少了10.1%。数据经最小二乘法拟合后，得到区域禁左MFD 一元二次回归方程为

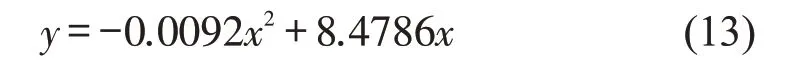
3.2.4 对比分析

由图8 可知：主干道(北京路)禁左对整体路网的交通优化效果最佳，对比未禁左时加权流量增加了13.8%，路网饱和流量增加了17.8%；单点禁左对交通优化效果次之；而区域禁左会阻碍交通，使得加权流量减少10.1%，路网饱和度降低17.8%。

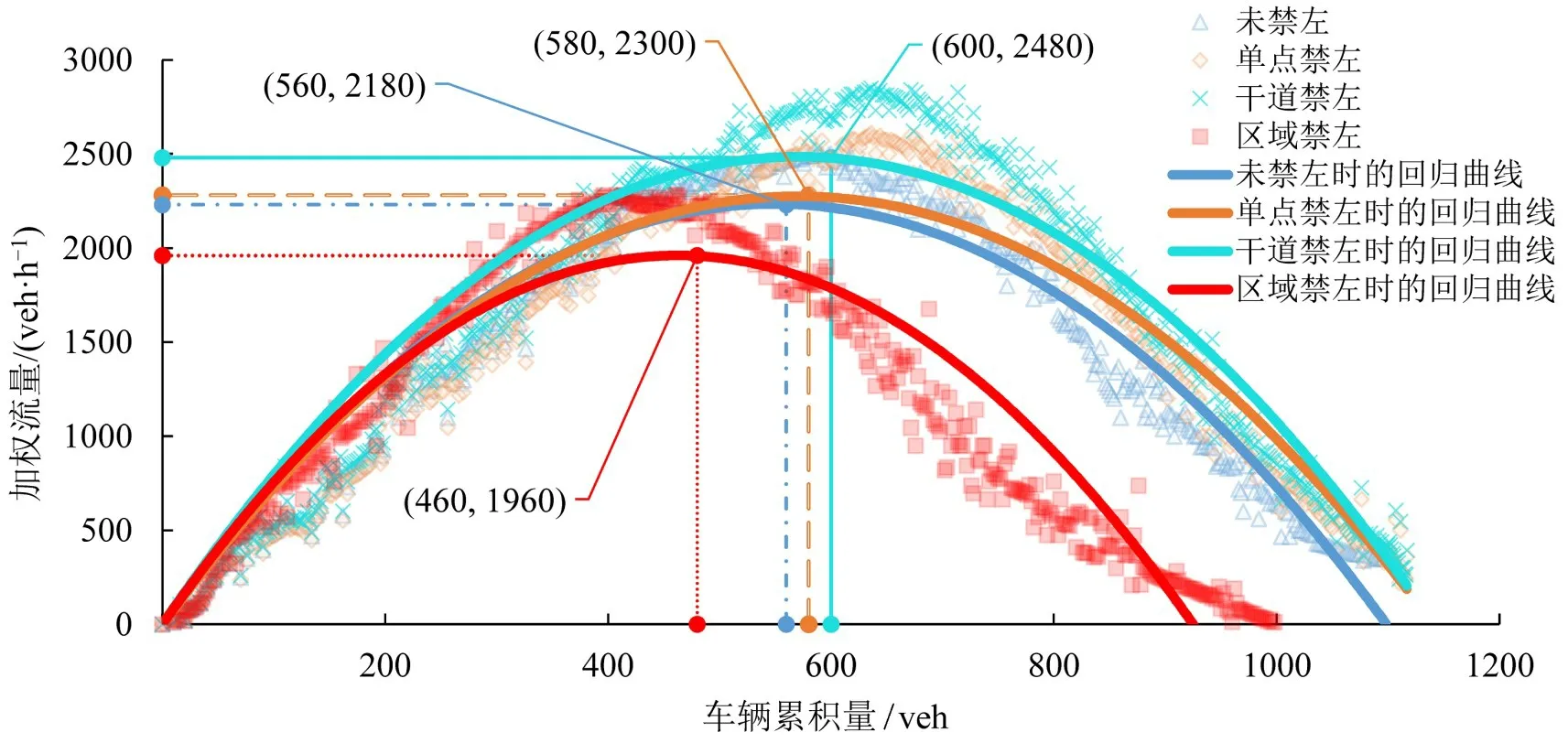
图8 不同禁左范围下的MFDFig.8 MFD of different left-turn prohibition ranges

3.3 不同左转车流比例禁左下MFD评价

上述仿真模型中所选用的每条路段的左转车流占全部车流的10%。为得出禁左交通组织的最优条件，选取左转车流占比作为设置禁左措施的影响因素，设置了左转车流占比为15%，20%，25%这3组仿真试验。

3.3.1 左转车流占比15%

将左转车流占比设为15%后，可得不同禁左范围下的MFD如图9所示。

图9(a)～图9(e)对应于北京路禁左路口，可以看出，图中MFD的形状并未发生较大改变，只有峰值流量发生较小波动。图9(a)对比图4 峰值点由(560,2180)变化为(560,2220)，由此可得，左转车流占比增加5%对未禁左时的交通运行效率没有影响；图9(b)对比图9(a)峰值点由(560,2220)变化为(580,2550)，加权流量增加了14.9%；图9(c)对比图9(a)峰值点由(560,2220)变化为(610,2380)，加权流量增加了7.2%；图9(d)对比图9(a)峰值点由(560,2220)变为(450,1860)，加权流量减少了16.2%；图9(e)表明当左转车流占全部车流的15%时，单点禁左对交通优化效果最佳，其中，加权流量增加了14.9%，饱和流量增加了3.6%；主干道(北京路)禁左后，路网运行也有所改善，加权流量增加了7.2%，饱和流量增加了8.9%；区域禁左会阻碍交通使得加权流量下降16.2%，饱和流量减少16.1%。

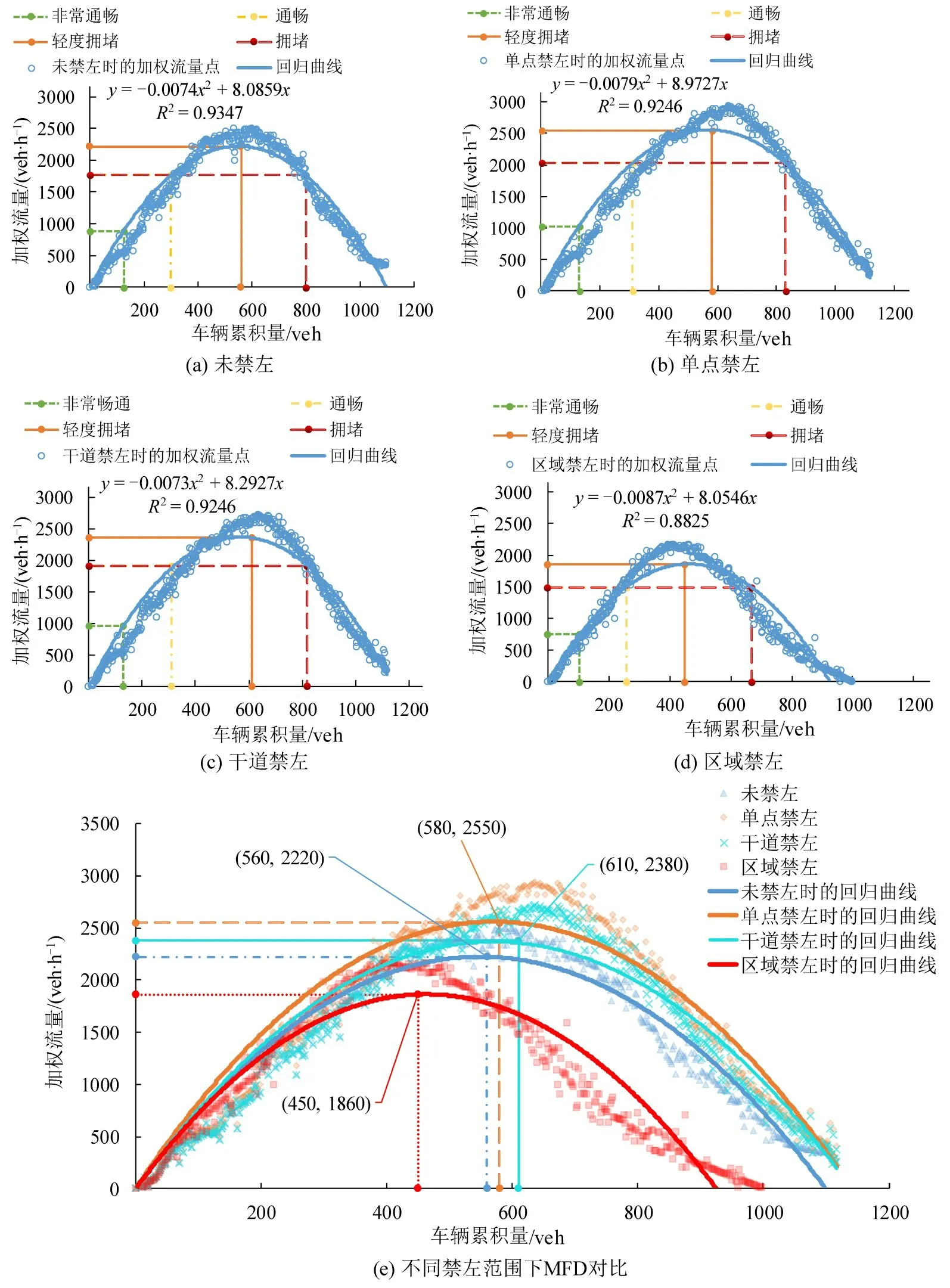
图9 不同禁左范围下的MFD(左转车流占比15%)Fig.9 MFD of different left-turn prohibition ranges(proportion of left-turn vehicles is 15%)

3.3.2 将左转车流的比值调至20%

将左转车流占比设为20%后，可得不同禁左范围下的MFD 如图10所示。可知，图10(a)～图10(e)中MFD的形状并未发生较大改变，图10(a)对比图4峰值点由(560,2180)变化为(550,2300)，对称轴向左平移了10 个单位，加权流量增加了120 个单位，由此可以得出左转车流占比增至20%对未禁左时的交通运行效率影响较小；图10(b)对比图10(a)峰值点由(550,2300)变化为(580,2440)，加权流量增加了6.1%；图10(c)对比图10(a)峰值点由(550,2300)变化为(600,2130)，加权流量减少了7.4%；图10(d)对比图10(a)峰值点由(550,2300)变为(480,1780)，加权流量减少了22.6%。当左转车流占全部车流的20%时，虽然主干道(北京路)禁左后的MFD中加权流量由未禁左时的2300 veh 减少到2130 veh，减少比例为7.4%，但是减少的车辆数较少，且在图10(e)中拟合二次函数的对称轴向右移动了50个单位，即饱和度增加了9.1%，说明此措施对实际车流容量影响更大，所以，此时主干道(北京路)禁左是可行的。综上，对于左转车流占总车流20%的情况，该区域单点禁左能有效增加路网通行能力；主干道禁左路网通行效率优化效果次之；区域禁左会降低路网通行能力。

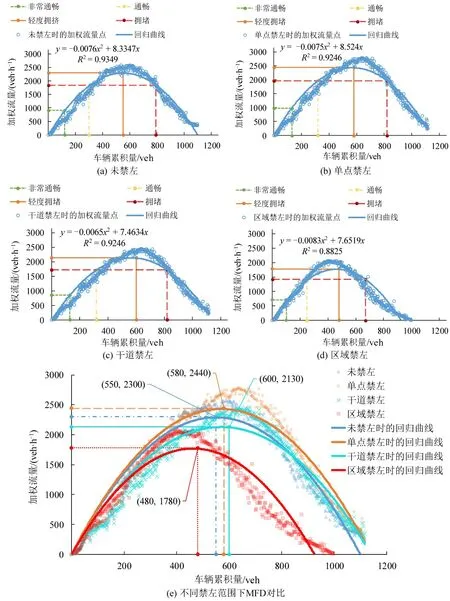
图10 不同禁左范围下的MFD(左转车流占比20%)Fig.10 MFD of different left-turn prohibition ranges(proportion of left-turn vehicles is 20%)

3.3.3 将左转车流的比值调至25%

将左转车流占比设为25%后，可得不同禁左范围下的MFD如图11所示。

图11(a)～图11(e)对应北京路的禁左路口，图中MFD 的形状并未发生较大改变，只有峰值流量发生了变化，图11(a)对比图4 峰值点由(560,2180)变化为(570,2220)，对称轴向左平移了10 个单位，加权流量增加了1.8%，由此可以得出左转车流占比增加至25%对未禁左时的路网通行能力影响较小；图11(b)对比图11(a)峰值点由(570,2220)变化为(590,2180)，加权流量减少了1.8%；图11(c)对比图11(a)峰值点由(570,2220)变化为(580,1900)，加权流量下降了14.4%；图11(d)对比图11(a)峰值点由(570,2220)变为(480,1600)，加权流量下降了27.9%。图11(e)将4 个MFD 进行对比分析得出禁左优化效果不明显。综上，当左转车流占全部车流的25%时，全区域内实施禁左都会降低路网通行效率。

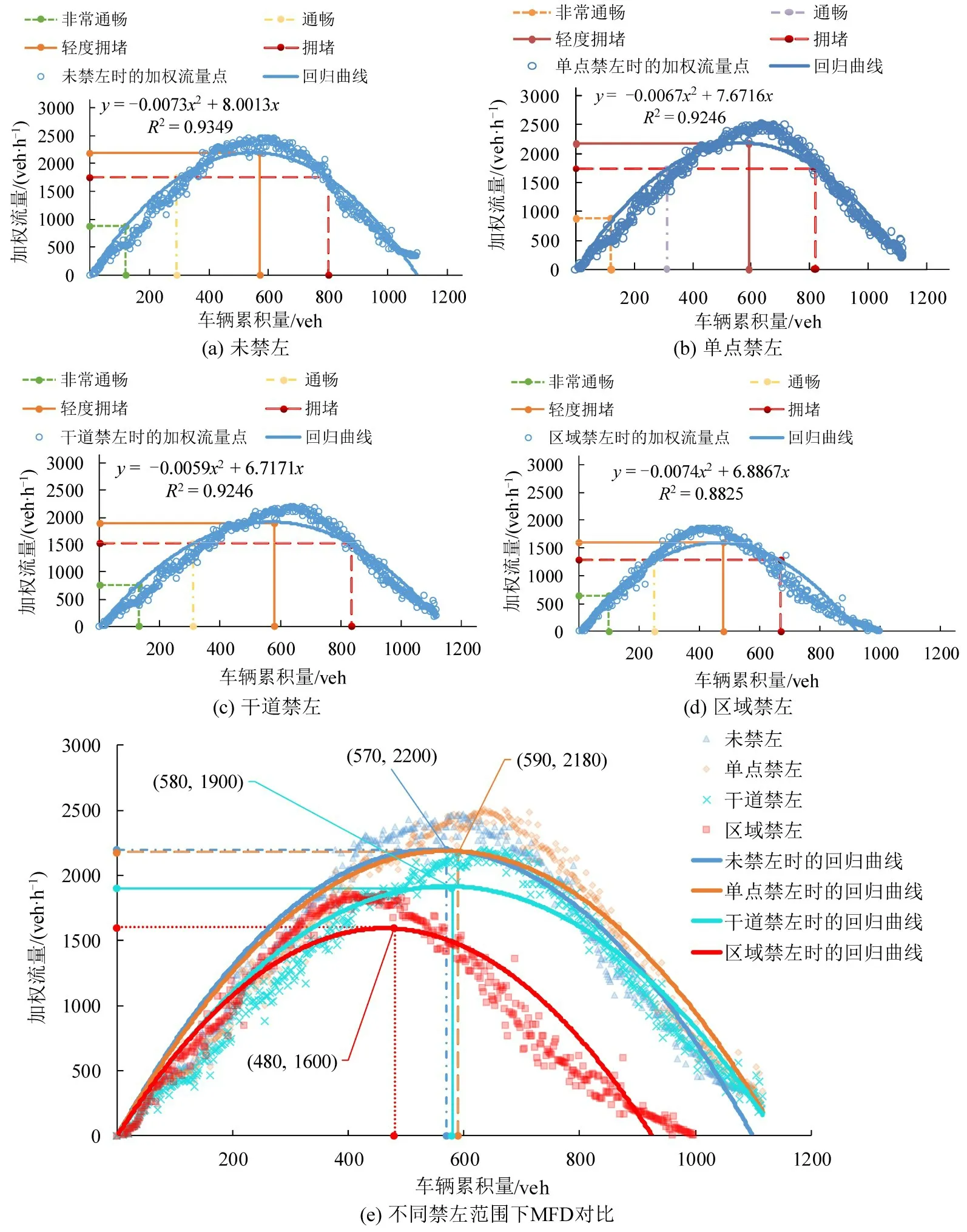
图11 不同禁左范围下的MFD(左转车流占比25%)Fig.11 MFD of different left-turn prohibition ranges(proportion of left-turn vehicles is 25%)

3.3.4 总结分析

不同区域和不同左转流量比例下的禁左下MFD对比分析如表2所示。

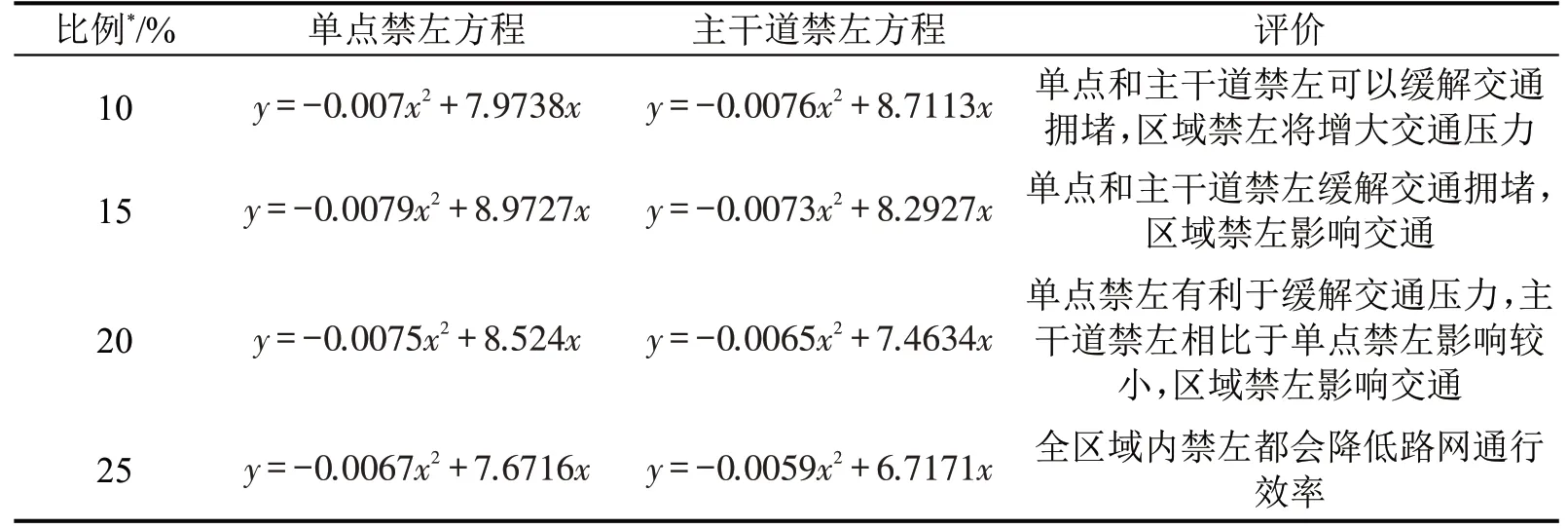
表2 不同范围和不同左转流量比例禁左下的MFD对比分析Table 2 Comparative analysis of MFD with different range and different left-turn flow ratio

通过MFD对不同区域和不同左转流量比例下的禁左措施分析可知：

(1)单点禁左。当左转车流占比小于20%时，有效提高路网的通行能力；当左转车流占比达25%及以上时，阻碍交通。

(2)主干道禁左。当左转车流占比小于15%时，有效缓解交通压力；当左转车流占比为20%时，缓解交通压力的能力有所下降；当左转车流占比大于20%时，阻碍交通。

(3)区域禁左时将阻碍交通。

综上所述，在该区域内，当左转车流占比小于15%，采用单点禁左或主干道禁左可以提升路网交通运行效率；当左转车流占比为15%～20%时，仅单点禁左可以提升路网交通运行效率；当左转车流占比大于20%时，所有干道禁左会降低交通运行效率。

4 结论

为科学评价单点、干道及区域等不同维度的禁左措施，本文基于MFD 区域性交通状态表征的优势，构建不同维度下禁左的MFD 交通状态评价模型，并对不同左转流量比例下的禁左方案进行分析，主要结论如下。

(1)研究结果表明：本文模型能有效评价单个交叉口、干道及区域禁左措施，为不同维度禁左提供理论依据；在本文所选的路网区域内通过仿真发现，当左转车流占比小于20%时，单点禁左能有效提高路网通行能力；在左转车流占比小于15%时，主干道禁左能有效缓解交通压力；全区域禁左只会阻碍交通。

(2)本文分析方法可以推广到不同区域的交叉口禁左组织评价，从宏观层面为交叉口禁左交通组织优化提供更加系统可靠的理论依据。