基于滚动时域优化的共享自动驾驶汽车动态调度方法

陈垚，柏赟*，张安英，毛保华，陈绍宽

(1.北京交通大学，综合交通运输大数据行业重点实验室，北京 100044；2.广东省交通运输规划研究中心，广州 510101)

0 引言

随着城市交通快速发展和科技水平高速提升，自动驾驶汽车[1]与共享出行[2]得到了国内外学者的众多关注。共享自动驾驶汽车(Shared Autonomous Vehicles，SAV)是两者相结合的产物。共享自动驾驶汽车可为出行者提供便捷的需求响应式服务，被视为未来城市交通系统的重要组成部分[3]。

在SAV运营过程中，系统通常需要进行两方面车辆调度，订单分配(Vehicle-trip Assignment)与空车移位(Empty Vehicle Relocation)[4]。一方面，在乘客发送订单后，订单分配需要决策系统是否服务该订单，若订单被接受，系统还需为其指派车辆。另一方面，由于乘客出行需求存在一定的方向性，在运营过程中部分区域可能出现空车堆积，而另外区域出现车辆短缺。因此，系统有必要进行空车移位，尽可能保证在需求位置处存在车辆供给，以提升车辆利用率。

乘客出行需求特征是SAV 车辆调度的主要依据[5]。车辆调度需适应乘客出行需求的时空分布。然而，车辆调度决策需要实时动态进行，由于未来时段的出行需求难以提前掌握，给车辆动态调度决策带来一定的难度。因此，基于历史出行需求规律制定科学合理的动态调度策略，对提高系统收益与提升乘客服务水平都至关重要。

国内外学者主要从社会影响[6]、乘客行为[7]、设施规划[8]和车队运营[4]等角度进行SAV 的相关研究。在车辆动态调度领域，部分学者基于仿真方法测试了不同启发式策略的运行效果。HYLAND等[9]利用Agent 仿真对比了6 种订单分配策略。HORL等[10]利用MATSim仿真平台分别评估了2种订单分配与2 种空车移位策略的效果。部分学者也对车辆动态调度优化展开研究。MAO等[11]利用深度强化学习提出了无模型下的空车移位策略。KANG 等[12]基于马尔科夫决策建立了等待乘客无流失下的车辆调度模型，从理论角度分析了SAV系统的最大可服务乘客数量。AL-KANJ 等[13]利用近似动态规划与值函数逼近建立共享自动驾驶电动汽车的动态调度方法，其调度策略涉及不同电量车辆的选派、空车移位与充电决策。然而，既有文献较少同时考虑订单分配与空车移位，尤其在订单分配时，较少考虑乘客等待时间限制。如何在乘客发送订单后，及时合理调度周边车辆还有待进一步探索。

鉴于此，本文综合订单分配与空车移位两方面决策，详细考虑乘客等待时间限制下的订单分配，研究SAV 系统的车辆动态调度问题。为便于问题建模，提出时空网络刻画车辆动态调度问题；并以时空节点流量为状态，以时空弧流量为决策变量，构造马尔科夫决策模型；采用滚动时域优化思想建立随机规划方法求解各时刻的动态决策结果；通过Sioux Falls网络验证方法的有效性。

1 问题描述与刻画

1.1 SAV动态调度问题

SAV系统主要由SAV车队、中央控制端与乘客3 部分组成。SAV 车队规模固定且不提供合乘服务。SAV 交通网络刻画为一系列空间位置点及连接路段。各位置点可视为邻近区域的聚类中心，以降低问题复杂程度。位置点表示为s、i或j，其集合表示为S。由于AV 车辆具有专用道路，两位置点间的行驶时间固定，位置i和j之间的行驶时间表示为lij。研究时段T离散为一系列等间隔的时刻，各时刻用t或k表示。

在研究时段内，乘客通过手机App等向系统发送出行订单。假设乘客发送的都是即时出发订单，无提前预约订单。出行信息包括当前出发时刻t，出行起点i及终点j，表示为(i,j,t)。乘客可等待时长固定为w，则乘客出发时间窗范围为[t,t+w]。中央控制端实时接收乘客订单，掌握所有SAV的位置与载客状态，并将订单分配给车辆。系统采取延迟集中分单策略(Batching Matching)，在时刻t集中分配时间段t-1 到t之间的订单。每个订单可以分配给3类车辆：在订单出行起点的空闲车辆，该类车辆可直接将乘客运送至目的地；在订单出行起点附近的空闲车辆，该类车辆需先前往订单起点接驾再运送乘客；处于载客状态但即将结束服务的车辆。该类车辆的上一订单终点位置需与当前订单起点位置相同或附近(也称为连续派单)。定义Si(l)表示距离位置i行程时间不超过l的位置点集合，即。因此，在乘客出发时间窗k∈[t,t+w]内，位置处于s∈Si(t+w-k)(即lsi≤t+w-k)的空闲车辆均可在t+w时刻之前到达位置点i。因此，对于订单(i,j,t)，在时刻k∈[t,t+w]空闲且位置处于s∈Si(t+w-k)的车辆均可被指派给该订单。SAV 系统通过完成乘客订单获取收益。用Psij表示车辆由位置s前往位置i将乘客运输至j的载客收益，主要包括载客收入减去s到i的接驾途中与i到j的运送途中的油耗等成本。

除订单分配外，系统还需要在各时刻上进行空车移位决策。系统决定是否将当前处于位置s的空车移动到另一位置j，以匹配乘客需求的空间分布。空车移位成本用Csj表示，主要包括s到j移车途中的油耗等成本。

综上，SAV动态调度问题可总结为中央控制端在运营时段内各个时刻根据乘客订单信息进行订单分配与空车移位，其目标为时间段内总收益最大化。

1.2 时空网络

为刻画SAV车辆调度问题，建立时空网络。时空节点n为二元数组(i,t)，表征时间与空间信息。时空弧e连接两个时空节点，其起终点表示为和，表示车辆运行。在任意时刻下，空闲车辆有3个选项：接受订单任务前往接送乘客，接受移位任务空驶移至其他位置以及原位置空车等待。因此，时空弧分为3 类：服务弧ESER、移位弧EREL与空闲弧EWAT。

(1)服务弧表征服务乘客出行下的车辆位置变化。对于每个订单(i,j,t)，生成服务弧子集。由于系统可指派时刻k∈[t,t+w]空闲且位置处于的车辆服务于订单(i,j,t)，对任意的，生成服务弧连接节点(s,k)与节点(j,t′)，其中，。该服务弧表示车辆在时刻k由位置s前往位置i接驾，再将乘客送往位置j。该服务弧的收益，服务弧的乘客等待时间。

(2)移位弧表征空车移位下的车辆位置变化。对任意的i∈S，j∈S和t∈T，生成移位弧e∈EREL连接节点(i,t)和节点(j,t+lij)，表示空闲车辆在时刻t由位置i移至位置j。该移位弧的收益。

(3)等待弧表征空车在原地等待指派。对任意i∈S和t∈T，生成等待弧e∈EWAT连接起点(i,t)和节点(i,t+1)。该等待弧表示车辆在时刻t位置i空闲。空闲弧的收益为0。

车辆调度时空网络示例如图1所示。

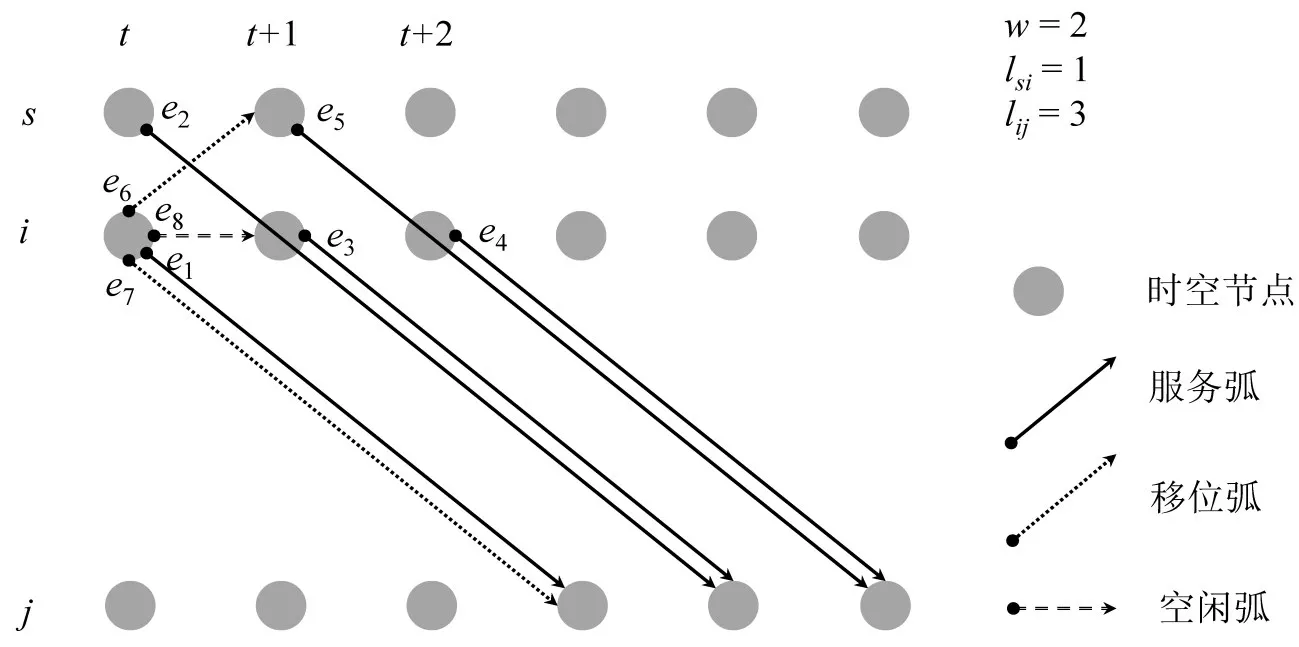
图1 车辆调度时空网络Fig.1 Time-space network for SAV fleet management

图1 中，在当前时刻t，对于订单(i,j,t)，服务弧e1表征当前处于位置i的空闲车辆用于服务该订单；服务弧e2表征当前处于相邻位置s的空闲车辆用于服务该订单(需先前往位置i接驾)；服务弧e3和e4表征将在时刻t+1和t+2 空闲且处于位置i的车辆用于服务该订单；服务弧e5表征将在时刻t+1 空闲且处于位置s的车辆用于服务该订单(先前往位置i接驾)。该5 个服务弧均属于。此

为刻画车辆动态调度问题，定义Nt表示时刻t对应的时空节点集合。定义Et为时刻t对应的时空弧集合，包括时刻t的订单对应的服务弧以及在时刻t出发的移位弧和等待弧。由于未来时刻的空闲车辆可用于连续派单，Et不仅包括所有Nt内节点出发的时空弧，也可能包括未来时刻对应时空节点出发的服务弧。外，当前处于位置i的空闲车辆可被空驶调度至位置s与j，表示为移位弧e6与e7；也可原地空闲等待，表示为等待弧e8。对于任意时空节点n，由该

2 模型构建

将每时刻视为一个阶段，车辆动态调度问题本质上是一个多阶段随机优化问题。可采用马尔科夫决策框架对问题进行建模[14]。模型框架主要包括5 部分要素：状态变量、外界信息、决策变量、状态转移方程与目标函数。

(1)状态变量

由于车辆在载客状态下不能接受乘客订单与空车移位，车辆状态定义为车辆最早处于空闲状态的时刻与位置。在当前时刻t，若车辆处于空闲状态，则状态变量刻画此时的车辆位置。若车辆在时刻t处于载客状态，状态变量不刻画其当前时刻位置，而刻画其载客结束后的时刻与位置。基于时空网络，可用时空节点n=(s,k)的车辆流量表征状态变量。表示根据时刻t信息，最早在时刻k空闲且处于位置s的车辆数。

(2)外界信息

在SAV系统中，中央控制端在各个时刻更新乘客的订单信息。在时刻t，订单信息表示为订单(i,j,t)的需求数。

(3)决策变量

在时刻t，系统需为当前订单指派车辆并对当前空闲车辆进行空车调度。基于时空网络，车辆调度行为可用集合Et内的时空弧表征。弧流量表示在时刻t按调度行为e∈Et执行的车辆数。

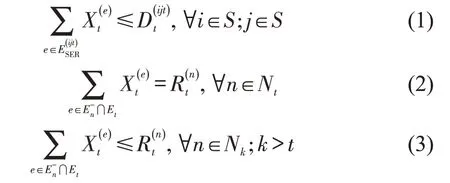
式(1)表示对于当前订单(i,j,t)，调度行为必须不超过订单的需求数。约束取小于意味着该订单中的部分需求被拒绝，未被派车的乘客将离开系统。值得注意的是，针对当前订单，可指派未来时刻的空闲车辆。式(2)为当前时刻的流平衡约束。在当前时刻节点n∈Nt的空闲车辆必须被全部调度(执行订单、空车移位或空车等待)以进入下一时刻。式(3)为未来时刻的流量限制约束。未来时刻的空闲车辆可用于连续派单。在未来时刻k(k ＞t)的节点n∈Nk，必须有足够的车辆数才可执行连续派单。

(4)状态转移方程

状态转移方程刻画系统从时刻t至t+1 的状态变化。由于车辆的行驶时间固定，可根据时刻t的状态与决策行为对时刻t+1的系统状态进行估计。

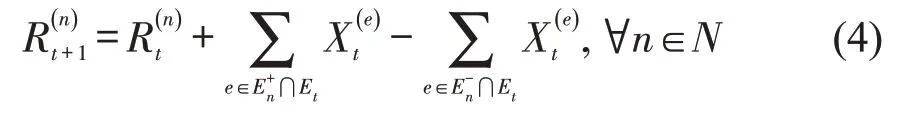
式(4)表示时刻t+1状态中，在时空节点n的空闲车辆数等于在时刻t已知空闲的车辆数加上决策后新增的空闲车辆数，以及减去决策后减少的空闲车辆数。

(5)目标函数

车辆动态调度的主要目标是最大化系统净收益。时刻t决策所产生的收益包括完成乘客订单服务的收益减去空车移位的成本，即

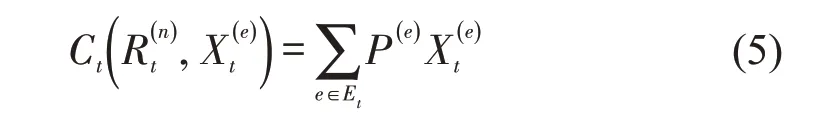
在研究时间段内，问题目标是使净收益总和的期望最大化，即

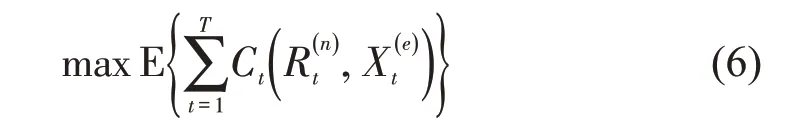
车辆动态调度问题既需要考虑当前时刻收益，也需要平衡调度方案对未来运营的影响。根据Bellman 最优原理，时刻t的决策需使当前时刻收益与未来收益期望值之和最大化。该问题递推表达式为

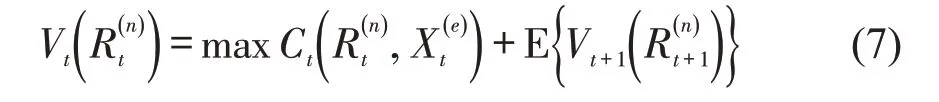
值得注意的是，对于一个订单而言，当既可指派给当前空闲车辆，也可连续派单给未来空闲车辆时，应优先指派当前空闲车辆。从乘客角度，可减少乘客的等待时间；从运营角度，有利于当前空闲车辆的使用，提高车辆的利用率。因此，系统决策可在净收益最大化基础上增加第2目标，即最小化乘客等待时间。

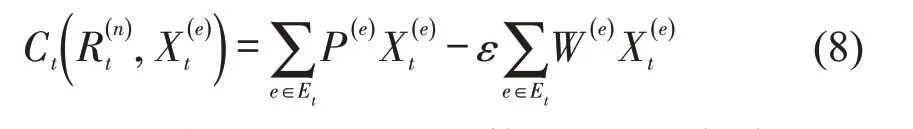
式中：ε为一个很小的权重系数，用于平衡首要目标与次要目标[15]。

3 基于滚动时域的随机规划方法

由于系统未来订单信息的随机性，式(7)中期望值难以通过数学表达式精确刻画。基于滚动时域优化思想[14]，本文滚动建立前视(Lookahead)时间窗，利用历史样本数据作为未来订单信息的估计，建立随机规划模型，以辅助当前时刻决策。

假设时间窗长度设h，时刻t的前视时间窗为。为考虑未来订单信息，根据历史数据生成样本集Ω。每个样本ω∈Ω提供未来时刻t′∈Ht的乘客订单需求作为输入。滚动时域框架下，系统在时刻t对整个时间窗内的车辆调度决策进行优化。既确定当前时刻t所对应的时空弧e∈Et的流量，也确定未来时刻t′∈Ht对应的时空弧e∈Et′的流量。决策变量为，后者表示在时间t根据样本ω决策下的时空弧e∈Et′的流量。只有e∈Et的决策结果被执行，e∈Et′的决策结果不被采用。

基于滚动时域优化，建立时刻t的随机规划模型为

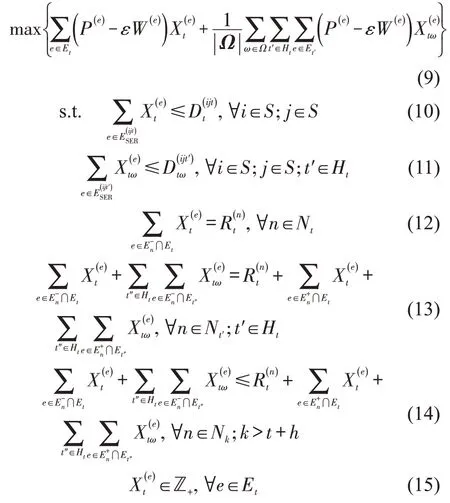
目标函数式(9)既包括最大化当前收益，也包括在各样本订单信息下未来时刻的平均收益，第2项可理解为式(7)中未来收益期望值的近似，为提升车辆调度决策效果，增加了第2目标最小化乘客等待时间。式(10)表示当前订单(i,j,t)的派单调度不超过订单的需求数。式(11)表示对于样本ω∈Ω，时间窗内订单(i,j,t′)的派单调度不超过订单的需求数。式(12)为当前时刻t的车辆流平衡约束。式(13)为时间窗内未来时刻t′∈Ht的车辆流平衡约束，其中，等式左边为从时空节点n出发的车辆数；等式右边第1项为时刻t已知在时空节点n的车辆数，等式右边第2 和第3项为到达时空节点n的车辆数。式(14)为时间窗后未来时刻的车辆流量限制约束。式(15)表示决策变量为整数。由于的决策结果不被采用，可采用连续变量以加快模型求解速度。该随机规划模型为混合整数线性规划模型，可用CPLEX等商业求解器直接求解。模型规模受时间窗长度与样本数量决定。

利用随机规划模型求解得到调度行为e∈Et的结果后，通过状态转移方程更新系统状态，即可进入下一时刻，并以此往复。

4 算例分析

4.1 基础数据

本文以Sioux Falls标准网络[16]为例验证所建立的模型与方法。网络包括24 个位置点和76 条弧段。位置点间行驶时间采用自由流时间。算例以3 h 为研究时段，以1 min 为时间间隔。在初始时刻，各位置点均有8辆空闲车辆。时段内两点间订单平均需求设为路网OD 出行量的1/100。时段内订单总需求约为3600。网络如图2所示。

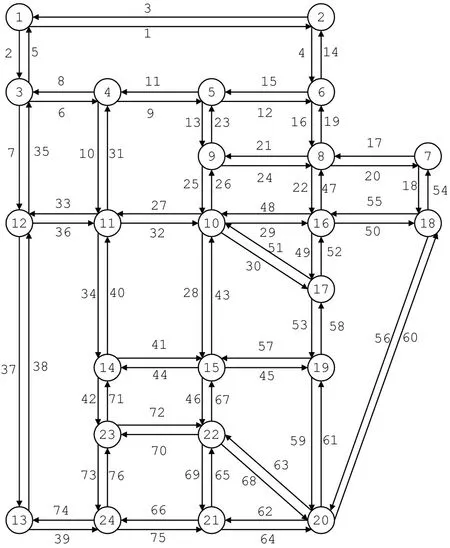
图2 Sioux Falls网络[16]Fig.2 Sioux Falls network

在研究时段内，两点间双方向的总需求呈对称分布。为模拟实际需求在早晚高峰时段的空间不对称性，在各小时内两点间双方向需求呈非对称分布。在第1 小时，主方向为S1～S12 去往S13～S24；在第3 小时，主方向为S13～S24 回到S1～S12。因此，第1小时起点在S1～S12和终点在S13～S24的订单数多于起点在S13～S24 和终点在S1～S12 的订单；在第2小时，双方向之间出行订单数量相同；在第3小时，起点在S1～S12和终点在S13～S24的订单数少于起点在S13～S24 和终点在S1～S12 的订单。两点间分小时出行需求比例如表1所示。

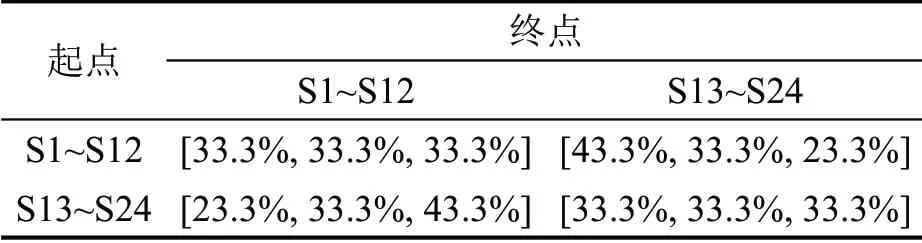
表1 两地点间分小时需求比例Table 1 Percentage of trip demand of three hours for each OD pair

为模拟订单需求的随机性，假设各时刻两点间的订单需求服从泊松分布，生成20 组数据样本。其中，10组为测试样本，作为当前订单信息的输入，用于测试算法效果；另外10组为历史样本，作为滚动时域优化的输入。订单服务价格为2.5元·min-1，空车移位成本为1 元·min-1，乘客可等待时间设为4 min。

4.2 滚动时域方法测试

为测试滚动时域方法效果，分析有和无滚动时域优化情形下的系统净收益。首先，不采用滚动时域优化，时间窗长度设为0(只考虑当前订单信息)，进行车辆调度决策；然后，采用滚动时域优化，对比车辆调度结果下的系统净收益。时间窗长度与样本集规模是影响滚动时域方法的关键，因此，设置不同的时间窗长度与样本集规模。针对10组测试样本，以采用滚动时域优化后SAV系统收益的提升比例为优化率，其结果如图3所示。这里随机规划模型均设置最小化乘客等待时间为第2目标。

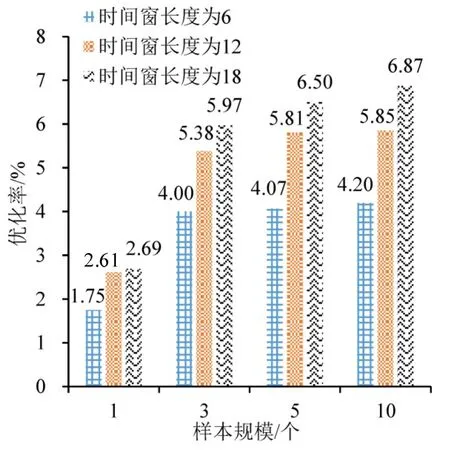
图3 滚动时域方法优化率Fig.3 Optimization results of rolling horizon method

如图3所示，相较于无滚动时域优化，采用滚动时域优化方法后，优化率均为正值。意味着系统净收益均有所提高，滚动时域优化方法可提升车辆调度决策效果。在给定样本规模下，时间窗长度越长，优化率呈上升趋势。这是因为随机规划模型可以考虑未来更长时间的影响。但随着时间窗长度的延长，优化率的上升有所减缓。另外，在样本规模较大时，延长时间窗长度可更加明显地提升优化率。在样本规模较小时，例如，只采用1 个样本，延长时间窗长度并未明显提高优化率。因此，滚动时域优化方法需要使用一定的样本量以保证优化效果。

在相同的时间窗长度下，随着样本规模的增加，优化率总体呈上升趋势。这是因为样本越多，未来收益期望值的近似误差越小。但优化率的上升随样本规模的增加而有所减缓。另外，当时间窗长度较短时(例如，时间窗长度为6)，增加样本规模(例如，样本规模从3 增加到10)优化率上升不明显。而当时间窗长度较长时(例如，时间窗长度为12)，增加样本规模可更加有效地提升滚动时域方法。

在计算时间方面，当不采用滚动时域优化时，每次决策所需时间约为0.01 s。而采取滚动时域优化时，所需的计算时间更长，如图4所示。

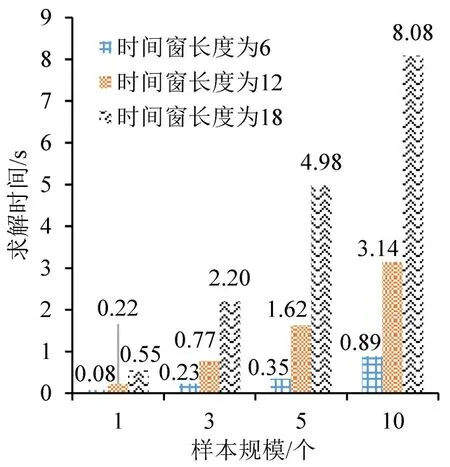
图4 滚动时域方法求解时间Fig.4 Computational time of rolling horizon method

由图4可知，时间窗长度越长，样本规模越大，随机规划模型所需要的求解时间也越长。在时间窗长度为12和样本规模为3时，每次决策的求解时间为0.77 s。当时间窗长度提升为18 或样本规模提升为5时，决策所需时间将超过1 s。

综合考虑优化效果与计算时间可以发现，在保证一定的样本规模和时间窗长度后，延长时间窗长度比增加样本规模效果更好。因此，为控制随机规划模型的求解时间，可采用长时间窗和中等样本规模。

4.3 车辆调度运营结果

以时间窗长度为12，样本规模为3 为例，采用滚动时域优化后的车辆调度运营结果指标如表2所示。其中，订单服务率为被服务的订单占订单需求的百分比，车辆利用率为车辆处于载客运行的时长百分比。

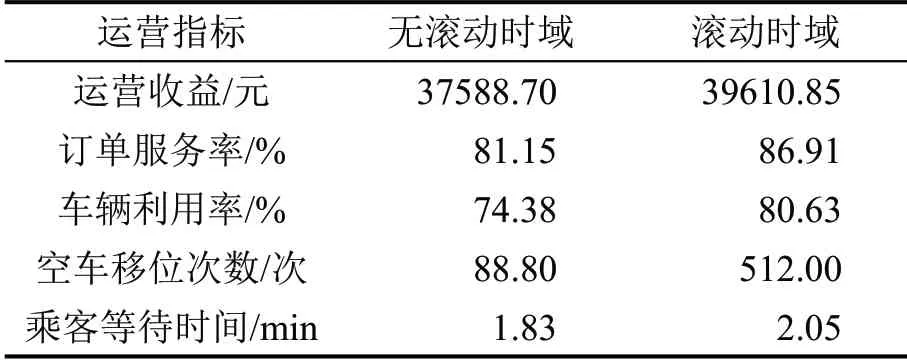
表2 车辆调度运营结果Table 2 Operational performance of SAV fleet management

与无滚动时域优化对比，当采取滚动时域优化后，运营收益提高了5.38%，车辆的利用率与订单的服务率均有所提升。结果表明，采用滚动时域优化进行车辆调度，既提高了系统的运营效率，也保证了乘客的出行。从空车移位次数明显增加可以看出，系统根据历史订单信息采取了合理的空车移位策略，使得系统运营效率提升。乘客等待时间略微上升，主要是因为系统车辆需要服务更多的订单，使乘客出现了更多地等待。

为测试随机规划模型中第2 目标对系统车辆调度的影响效果，在目标函数中不考虑最小化乘客等待时间，仅考虑最大化系统净收益。其车辆调度运营结果如表3所示。

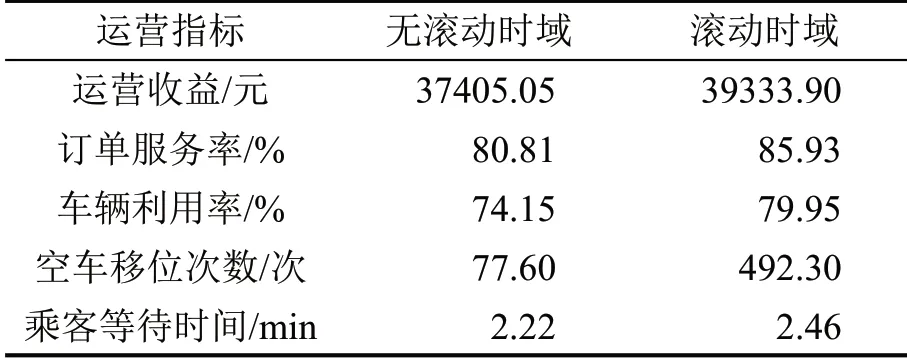
表3 车辆调度运营结果(不最小化乘客等待时间)Table 3 Performance of fleet management(without minimizing passenger waiting time)

对比表2 和表3 可知，将最小化乘客等待时间设为第2 目标，可有效减少乘客等待时间。同时，系统净收益、订单服务率与车辆利用率等指标也同步提升。在车辆动态调度问题中，若目标函数只考虑最大化系统净收益，仅能保证当前时刻净收益最大，会忽略车辆调度结果对未来运营的影响。因此，进一步考虑乘客等待时间非常必要。

4.4 连续派单影响

为测试连续派单对系统运营调度的影响，假设不采取连续派单模式。系统只将订单指派给当前空闲车辆，即第1类与第2类车辆，不能指派给当前未结束服务的车辆。采用滚动时域优化方法，车辆调度运营结果如表4所示。

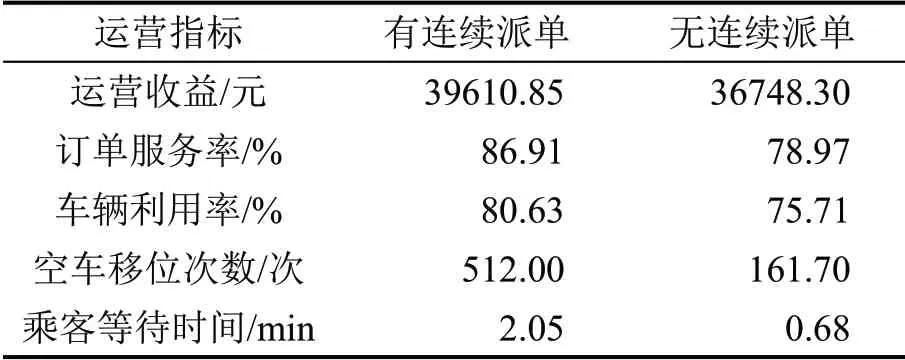
表4 无连续派单下的车辆调度运营结果Table 4 Performance of fleet management without continue assignment

由表4 可知，在无连续派单情况下，系统收益下降达7.22%。由于未结束服务的车辆不能够接单，车辆利用率由80.63%降至75.71%，乘客订单也更难被服务，订单服务率由86.91%降至78.97%。由于乘客均由当前空闲车辆服务，其等待时间减短至0.68 min。由于车辆可被使用的机会下降，空车移位次数也相应减少。

4.5 乘客可等待时间影响

为测试乘客可等待时间对系统运营的影响，假设乘客可等待时间为0 min或2 min，车辆调度运营结果如表5所示。

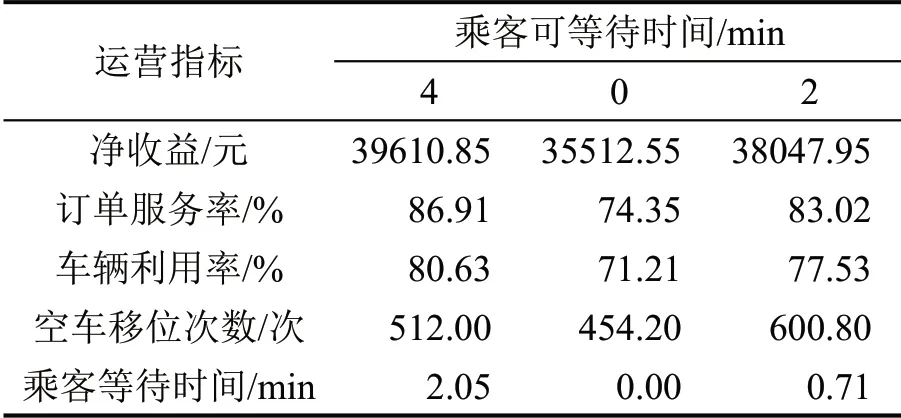
表5 不同乘客可等待时间下的车辆调度运营结果Table 5 Performance of fleet management without maximum waiting time

当乘客可等待时间为0时，乘客订单只能分配给处于起点位置的空闲车辆，车辆利用率降为71.21%，订单服务率也降为74.35%，系统运营收益下降了10.4%。由于可服务的订单更少，空车移位次数也更少。当乘客可等待时间为2 min 时，系统运营收益和车辆利用率与订单服务率相比可等待时间为0 时均有所上升。空车移位次数甚至相比乘客可等待时间为4 min时更多。这是因为乘客可等待时间为4 min 时，系统不需要空车移位也可以保证订单服务率。

5 结论

本文通过构造SAV 车辆调度时空网络，分别针对订单分配与空车移位生成对应的车辆运行时空弧，建立了车辆动态调度的马尔科夫决策模型，并针对模型设计了基于滚动时域优化的随机规划方法。

Sioux Falls 网络算例结果表明，采用滚动时域优化方法比不采用滚动时域优化方法的车辆调度决策效果更好。时间窗长度越长，样本规模越大，滚动时域方法的优化效果越显著；但因计算时间限制，应优先采用长时间窗中等规模样本。采用滚动时域优化方法时，在最大化系统收益的同时进一步最小化乘客等待时间，既可提高运营商收益，也可以降低乘客等待时间。采用连续派单方式可明显提高系统运营效率，车辆利用率和订单服务率均得到大幅提升。乘客可等待时间对系统运营有显著影响，乘客可等待时间越长，系统运营收益越大，有必要在车辆调度过程中考虑乘客可等待时间。