基于离散价格的高铁差异化定价优化研究

王煜，苗蕾

(1.中国铁道科学研究院，电子计算技术研究所，北京 100044；2.中国国家铁路集团有限公司，北京 100081)

0 引言

随着近年来铁路改革向深水区推进，以市场化为导向的发展趋势越来越明显。为了充分利用价格手段提高铁路的市场竞争力，急需打破原来一成不变的票价策略，实施以票价差异化为代表的高铁旅客列车定价方案[1]。自2020年12月23日开始，铁路运输企业在京沪高速线上实施差异化定价方案，即设置数档折扣，形成折扣档位，每趟列车同一席别在整个预售期内选择其中一档折扣档位执行，从而在不同的列车间呈现出不同的票价。差异化票价方案改变了之前一成不变的票价现状，满足各群体旅客乘车需求，对于均衡运输资源，调节客流需求，提高高铁竞争力无疑有重要的意义。

现有已公开发表的交通运输领域定价理论方法或模型内容丰富。Belobaba P.P.[2]最早将期望边际座位收益概念应用于航空收益管理，开创了后来基于期望收益研究定价问题的渊源。文献[3]继承期望收益概念，发现以期望收益最大化来判断是否要出售折扣票。文献[4]着重考虑了旅客出行选择行为。文献[5]假设顾客根据多项Logit模型进行购买决策，在此基础上研究一个具有网络效应的多产品动态定价问题。文献[6]利用博弈论模型研究相关替代品之间的动态定价问题。文献[7]假设需求是价格的函数，构建指数表达需求函数，得到了最优值函数的封闭解。文献[8]构建了基于多列车多停站的票额和票价综合优化模型，根据模型特点设计混合启发式算法进行求解，从而得到不同列车在不同区段的不同定价，解决差异化定价的问题。文献[9]以企业利润和旅客福利作为高铁定价目标，利用分层序列思想分解多目标问题，最终确定多目标定价最优策略。文献[10]利用潜在类别模型对高铁旅客进行细分，得到旅客对平行车次不同服务属性，引入收益管理，以多列车整体收益最大化为目标，构建平行车次动态差别定价模型。文献[11]以时间敏感性，价格敏感性及出发时段偏好为基础，对旅客进行分类，再研究同一区段两列平行列车的动态定价问题。文献[12-13]首先模拟旅客需求函数，得到描述客运产品的需求与票价的数学关系，再逐步构建高铁动态票价优化模型并求解。以上理论方法严谨、科学，具有很好的借鉴意义。但在以下几个方面仍缺乏考虑：(1)现阶段大多数定价理论将重点放在符合收益管理思想的动态定价上，即将预售期划分为多个时段，票价在预售期内浮动调整，而本文研究的差异化定价中同一列车在预售期内价格保持不变，是基于旅客分类和选择的差别定价；(2)目前大多数定价理论模型输出的最优定价结果为连续值，很少研究从价格制定者角度出发的基于离散价格(价格集)的差异化定价模型并构建求解算法[14]；(3)由于以价格维度衡量的非集计旅客数据较难获取，现有理论模型较少精确考虑构建基于价格敏感性的旅客分类，以及在此分类基础上的总体弹性需求函数；(4)现有理论模型在构造旅客效用函数时，较少考虑乘车出发、到达时间在不同时间段给旅客带来的额外机会成本。基于以上几点分析，本文提出一种基于离散价格的高铁动车组差异化定价优化模型[15-16]。

1 变量定义与假设

为简化问题，减少模型求解的计算量，本文做出如下假设：

(1)不考虑退票、改签对本文定价过程的影响。

(2)不考虑上车补票等超售行为。

主要参数及其含义如表1所示。

表1 主要参数及定义Table 1 Main parameters and definitions

2 问题描述与价格离散化

假设在预售期外，一条线路W，该线路公布票价率为z；线路涉及列车(车次)集合K，任意列车为k,∀k∈K。价格离散化可以描述为：制定折扣率集合B，包含M档(个)折扣率，第m档折扣率βm为

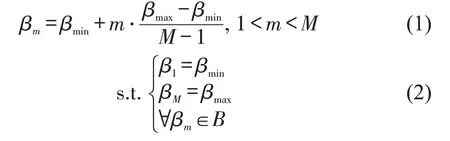
βm对应的票价率zm为

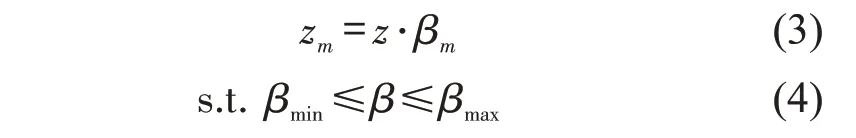
则列车k在od(r,s)上的票价为

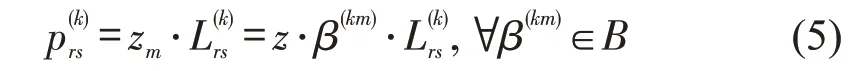
由于r，为常数，本文研究的问题转化为先确定βm，1 ≤m≤M，组成折扣率集合B，即为价格(折扣率)离散化集合。以收益最大化为目标并为每趟列车选择一个折扣率βm，得到β(km)，即βm→β(km)，∀k∈K。下面将研究βm→β(km)的过程。

3 模型构建

3.1 客流弹性需求函数与旅客选择分析

旅客乘车出行最关心耗费的金钱成本和时间成本，根据每位旅客对金钱和时间的偏好不同将旅客群体分类，分类依据是该名旅客历史乘车记录，如果某位旅客总是选择乘坐价格便宜的列车说明其价格敏感度较高，该群体选择用时间换金钱，时间成本在总效用中的影响程度较低。反之，总是乘坐高票价的旅客选择用金钱换时间，时间成本在总效用中影响较高。对于每类旅客群体分别拟合弹性需求函数，最后将各群体弹性需求函数加总得到全体旅客的弹性客流。本文研究定价问题，即主要以旅客对价格的敏感性高低进行分类，划分出J个不同的旅客群体，分类结果如表2所示。

表2 旅客群体分类Table 2 Classification of passengers

表2中，εj为划分旅客群体的阈值。od(r,s)涉及的列车平均运行时间为trs，平均票价prs[17]分别为

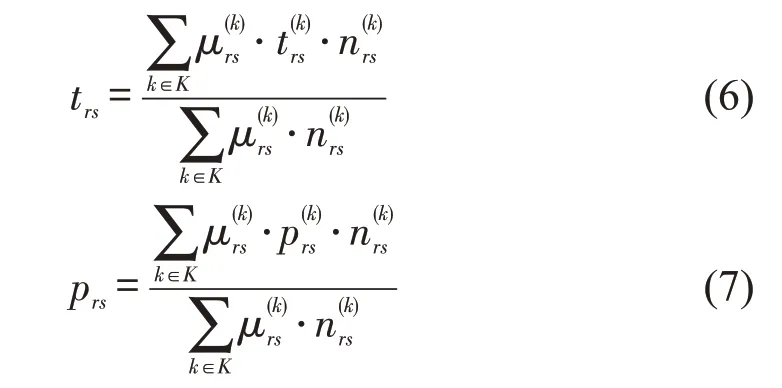
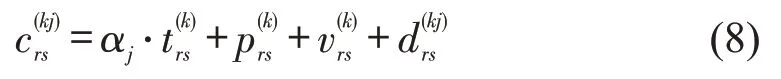
表3 时间段划分依据Table 3 Time period division basis

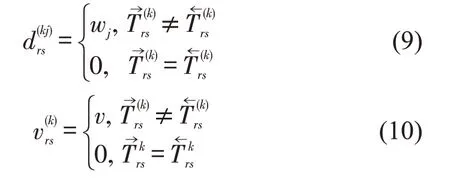
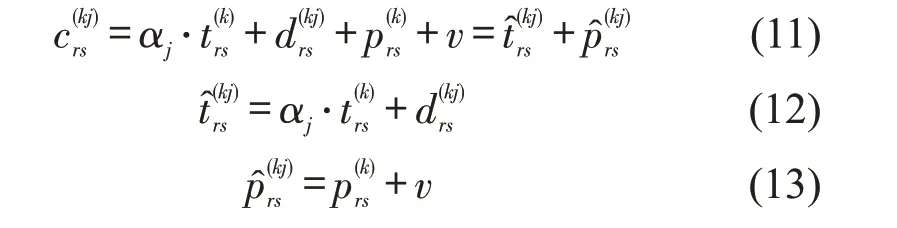
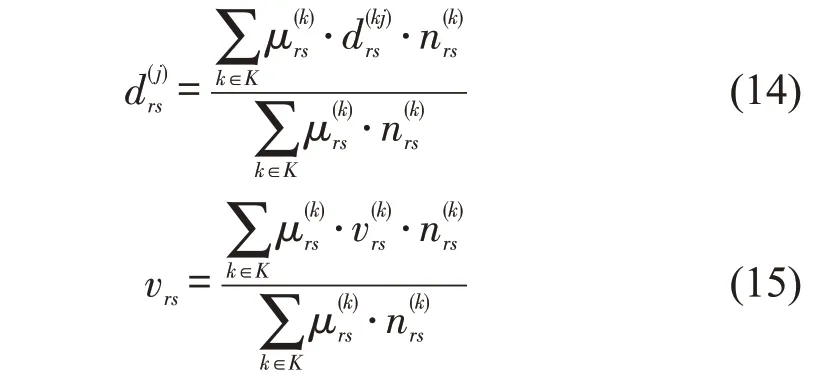
则od(r,s)上涉及所有列车对于各旅客群体的平均广义出行费为

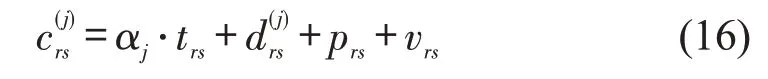
假设旅客出行需求用弹性需求函数拟合，则od(r,s)的旅客群体j出行需求弹性函数为

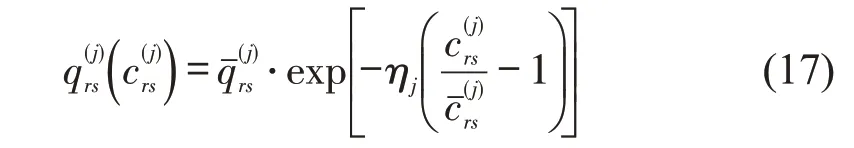
假设旅客乘坐列车获得的效用与广义费用成反比，对于od(r,s)的旅客群体j在列车集合中选择乘坐列车k的概率可以用多项Logit 模型进行描述，即

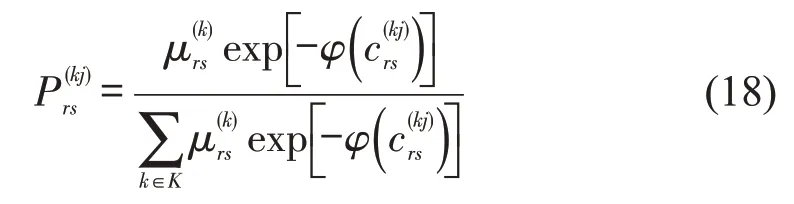
则列车k在od(r,s)的弹性需求函数为

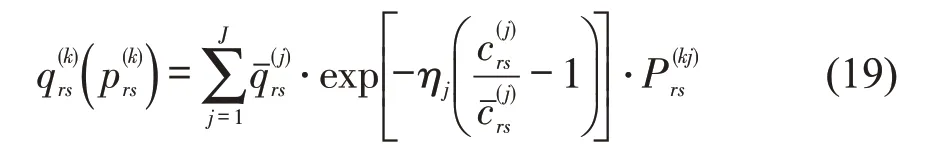
3.2 基于离散价格的差异化定价优化模型

列车k在od(r,s)上的售票量为

因此，列车k在od(r,s)上期望收益为

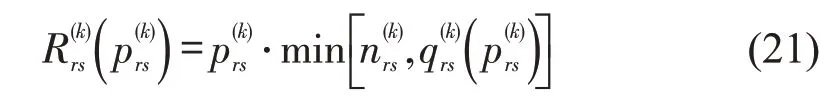
铁路运输企业在该条线路的期望收益最大化目标函数为

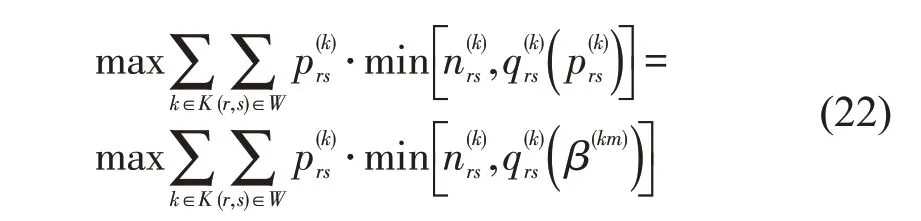
同时，还需要满足一些实际约束条件：

(1)折扣范围约束

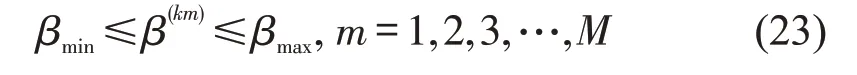
(2)价格离散化约束

(3)列车能力约束

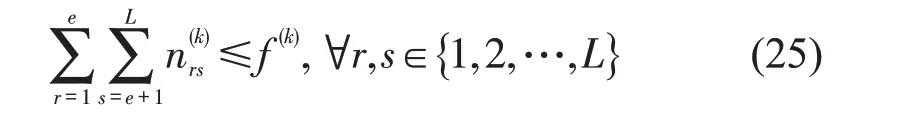
最终，得到在离散价格基础下以收益最大化为目标的差异化定价优化模型为

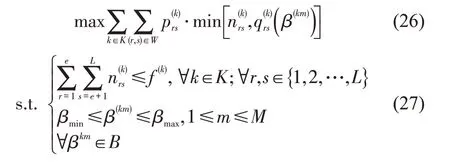
4 算法求解

由于本文优化模型是建立在离散价格基础上的，为了保证每次解都为档位的折扣率值，需要控制每次更新迭代的步幅，综合考虑迭代计算复杂度和集群系统现有计算能力，选择粒子群算法作为求解算法，其过程具体如下。

(1)确定M档折扣率集合B，将目前的各趟列车实际执行的票价折扣率按照就近原则转化为集合B的某个折扣值，组成初始解，解的每个分向量对应每趟列车的执行票价折扣率。设定粒子规模为Psize，第h个粒子的初始位置记为，且

式中：gh为与A维度相同的向量，且各分量服从表4的离散分布。

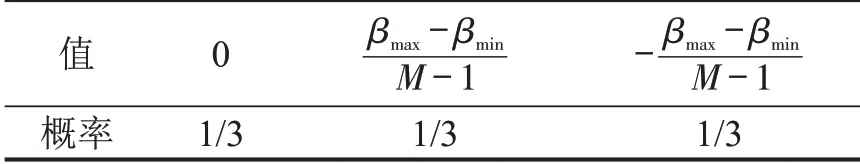
表4 gh 各分量概率分布Table 4 Probability distribution of each dimension of gh

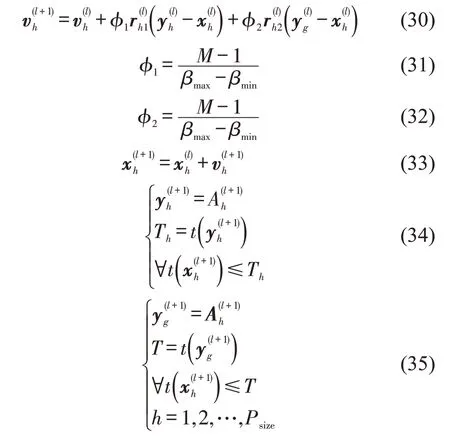
式中：Th为第h个粒子历史最佳位置的适应值；T为所有粒子历史最佳位置的适应值；为与A维度相同的向量，且各分量服从表5 的概率分布，用来描述求解算法迭代过程的随机性。

表5 与各分量概率分布Table 5 Probability distribution of each dimension ofand

表5 与各分量概率分布Table 5 Probability distribution of each dimension ofand

值概率0 1/3 1 1/3-1 1/3

本文求解算法过程如图1所示。

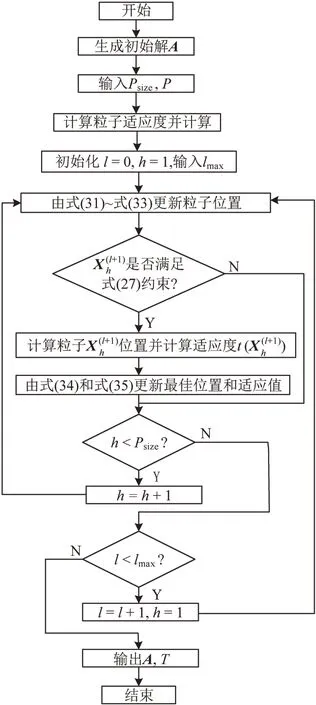
图1 算法求解过程Fig.1 Algorithm process

5 算例分析

5.1 基础数据

选择京沪高速线上海虹桥至北京南方向11 趟列车二等座为研究对象。列车开行主要特征选取时间为2021年5月5日。11 趟列车全程运行时间大致分为3 类：运行约4.5 h 的标杆车产品，包括G22，G4，G10；运行约5.5 h 的普通列车产品，如G124，G134，G156；运行约6 h 的列车产品，如G104，G102，G108，G138，G140。全程运行时间、定员、始发时刻、终到时刻等主要信息如表6所示。停站情况和各区间到达时刻情况如表7所示。

表6 列车开行情况Table 6 Train details

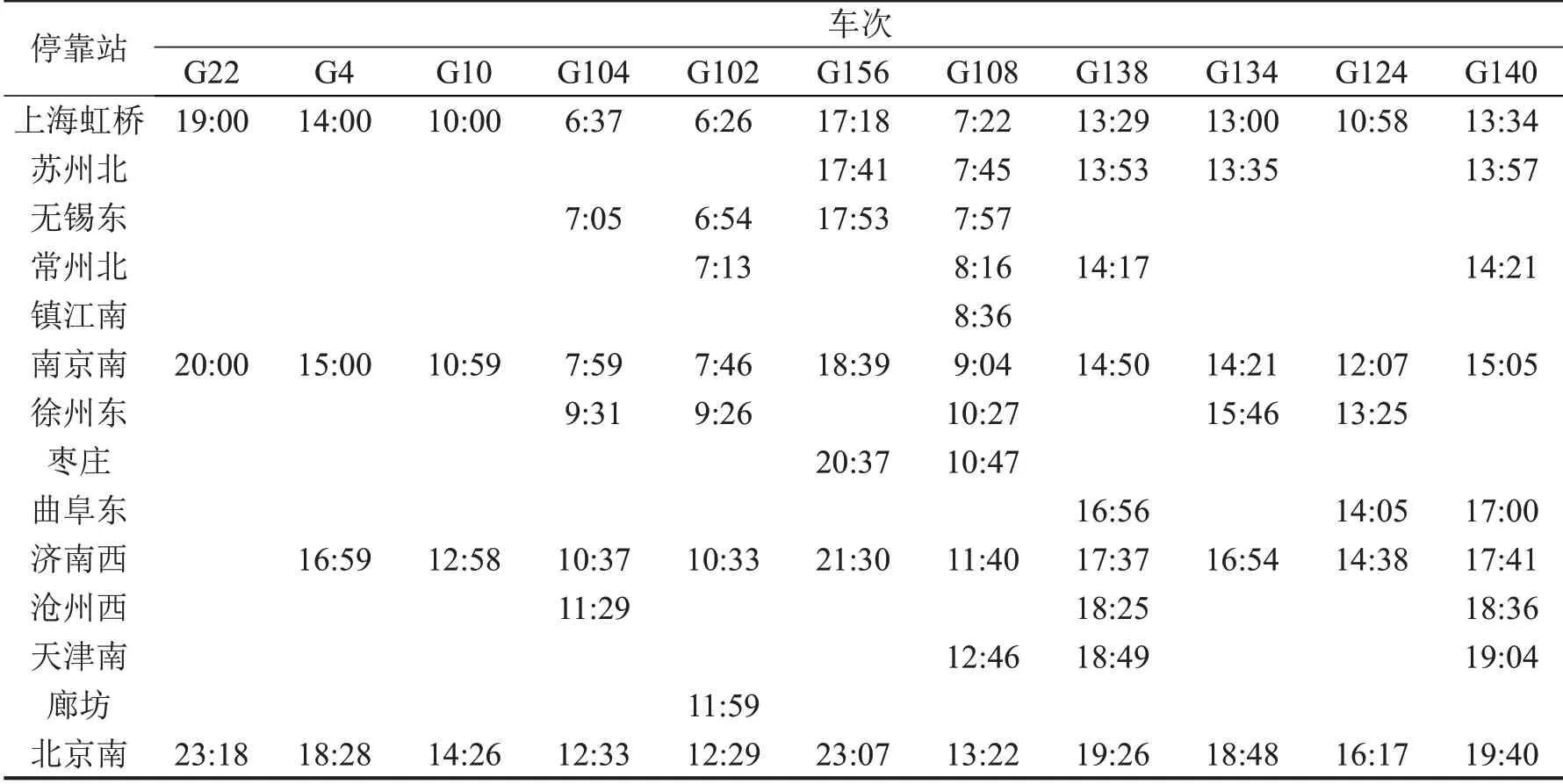
表7 主要停靠站及到达时刻Table 7 Stop and arrival time

选择2021年1月1日～5月5日为样本日期，主要OD区间日均发送量如表8所示。

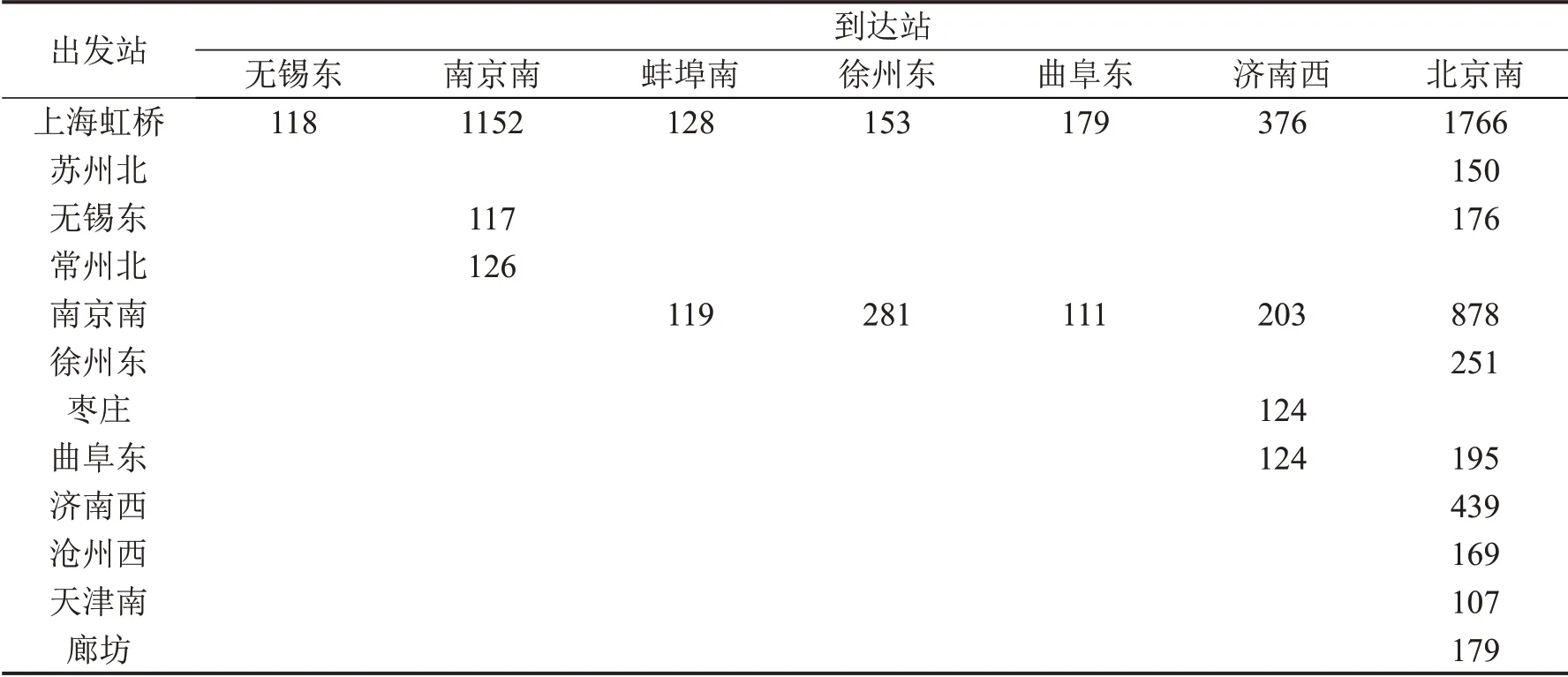
表8 主要OD日均旅客发送量Table 8 Average daily passenger volume in main OD(人次)

为简化问题，通过表2 的划分依据，取ε1=ε2…=εj-1=prs，即将所有旅客划分为经济型旅客和商务型旅客两类。通过样本估计经济型旅客群体平均占比约为57%，其余为商务型旅客。

折扣率最低值取5.5折，最高折扣为不打折，即βmin=0.55，βmax=1.00。根据文献[10]取φ=0.8，在时间价值转化系数取值的基础上，估算经济型旅客群体时间价值转化系数约为30，商务型旅客群体时间价值转化系数约为44，α1=30，α2=44。列车盒饭45元，v=45。当地每小时工资最低标准为12元，则w1=10，w2=14。

5.2 结果分析

令M=6，则折扣率档位如表9所示。初始解为2021年5月5日，11趟列车在京沪高速线上实际执行票价对应的表9 中最接近的折扣率组成。选取粒子数量Psize=50，最大迭代次数l=300。最终迭代过程如图2所示。

表9 6档折扣率Table 9 Six kind of discount

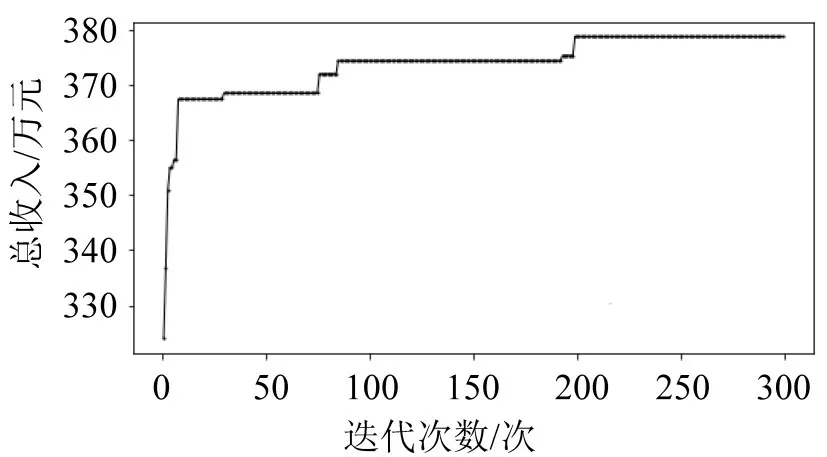
图2 算法迭代过程Fig.2 Iterative process of algorithm

由图2 可知，算法在迭代200 次时收敛至最大值，得到总体收入377 万元，比目前实际执行方案对应的日均367 万元总体收入提高11 万元，提高2.7%。具体输出的折扣率档位结果如表10所示。

表10 6档折扣率下差异化票价方案对比Table 10 Comparison of price scheme under 6 kind of discounts

5.3 折扣率档位数量的影响

考虑M=11 的情况，对应的折扣率如表11所示。11档折扣率集合选取粒子数量Psize=20，最大迭代次数l=300。训练10 次，取10 次中使目标函数式(26)取最大值的折扣率结果。

表11 11档折扣率Table 11 Eleven kind of discounts

当M=11 时，差异化定价优化结果如表12所示。总体收益为378万元，比实际执行方案对应的日均367万元提高12万元，提高3%。

表12 11档折扣率下差异化票价方案对比Table 12 Comparison of price scheme under eleven kind of discounts

6 结论

本文从价格管理实践问题入手，提出一种基于离散价格的差异化定价方法。以京沪高速线上海虹桥—北京南的11趟列车为算例证明本文提出的差异化定价方法在现行开行方案下能够有效提高总体收益，增强铁路市场竞争力[19]，同时可以看出：

(1)随着折扣率档位数量的增加(从6档增加到11档)，在保证足够迭代次数和训练次数的情况下，基于离散价格的差异化定价优化模型输出的折扣率结果取得的总体收益增大。当limM→+∞时，离散价格就转化为连续价格，也就是目前大多数定价优化问题的范式。

(2)目前大多数定价优化问题很多情况下需要通过启发式算法求解，求解过程通过控制步幅、方向在一个多维的向量空间搜索、迭代、更新，获取目标函数极值的票价结果。由于搜索步幅不可能无限小，因而本质上求解过程可以近似于一种离散价格基础上的求解。

(3)综上所述，目前大多数输出为连续值的定价优化问题可以看作是基于离散价格定价问题的一个特例。同时，基于离散价格的设定可以较好地与生产系统对接，有利于直接落地应用，兼顾理论科学性和应用实践性，因而基于离散价格的假设更接近于定价优化问题的实际。但另一方面，折扣率档位数量的确定需要考虑消耗的硬件设备资源和求解迭代时间，折扣率档位数量增多给价格管理人员带来更大的管理工作量，实践中应尽可能取得定价优化结果与所需求解时间的平衡。