基于改进点－弧模型的铁路网车流径路优化模型研究

高明瑶，石红国

（西南交通大学 交通运输与物流学院，四川 成都 611756)

0 引言

车流径路问题是在给定的路网环境中，确定各支车流的运行径路，使车流总走行费用最小的问题，是铁路网规划及铁路货物运输组织的重要工作之一，是车流组织工作的核心内容。合理恰当的车流径路能够促进铁路生产，提高铁路运输部门的效率和效益，对于均衡利用各个车站区间的能力，降低路网车流运输费用，提高铁路运营效益具有重大的意义。

众多学者对铁路网车流径路优化进行了很多的研究。例如，纪丽君等[1]建立基于多商品流模型的铁路网车辆分配和径路优化模型，并以我国东北地区局部铁路网为例，验证了模型的有效性和合理性；农静等[2]将铁路网车流径路的优化问题分解为离散空间中车流排列优化问题和车流排列的评价问题，并将其转化为旅行商问题，采用遗传算法求解；林柏梁等[3]通过确定合理路径集的方法，建立路网车流径路优化0-1 规划模型，并采用模拟退火算法求解；施其洲[4]对路网双向重空车流径路同时进行优化，解决了以往只对重车车流径路优化的问题；王保华等[5]考虑不确定情况下的车流径路优化问题，并提出一种随机模拟的混合遗传算法；田亚明等[6]研究了车流分配过程中的不可行流问题，采用虚拟弧计算不可行流；林柏梁等[7]考虑不同种类车流权重的差异，提出带权重的车流径路优化方法；苏顺虎等[8]以运输时间最少，运输距离最短，运输费用最低为目标构建多目标0-1 规划模型，并验证了该模型的有效性。

既有车流径路相关研究对节省运输费用及运输时间起到了一定作用，但是仍然存在着一些不足之处，如既有的点－弧模型可能在车流的分配过程中对车流进行了拆分，且无法准确获取车流径路。为此，针对点－弧模型的缺陷，遵循车流不拆散原理，在满足弧的能力约束，节点流量守恒约束的情况下，以车流总走行费用最小为目标函数，构建基于改进点－弧模型的铁路网车辆径路优化模型，为铁路网车流径路优化提供理论依据。

1 基于改进点－弧模型的铁路网车流径路模型

1.1 问题描述

将铁路网中的分支点车站和路段抽象为网络中的节点和弧，构建包含若干车站和路段的铁路网络，则网络可以描述为G= (V，E，C，W)。其中，G表示整个铁路网；V表示铁路网上的车站集合，记为V= {1，2，…，n}，n为车站的数量；E表示铁路网中弧的集合，E= {(i，j) |i，j∈V}；C表示铁路网中路段的能力约束集合，C= {cij，i，j∈V}，cij为从i站到j站的能力约束；W表示表示铁路网中路段的单位运输费用集合，W= {wij，i，j∈V}，wij为从i站到j站的单位运输费用。

考虑基于改进点－弧模型的完整性与简洁性，提出以下假设：①车流无改编通过途中分支点车站；②车站的接发能力足够大；③不考虑车流通过分支点车站的费用；④任意2 个车站之间的车流量已知；⑤同一支车流具有相同的车流径路，即车流不可拆散。

1.2 基于改进点－弧模型的铁路网车流径路优化模型构建

点－弧模型是以路网中车站和弧段为研究对象设置变量建立模型的，决策变量是各个弧段上的流量，根据中间点流入量等于流出量这一基本核心规律列出约束条件进行求解。由于点－弧模型中决策变量是各个弧上的流量，该流量是多股OD 间的车流量的总和，因而模型结果无法直观显示各股车辆的最优径路。

针对既有的点－弧模型的局限性进行改进：①引入0-1 变量，使得车流径路满足遵循车流不拆散的基本原理，同时使得优化结果能够体现车流径路；②结合实际铁路网中的运输情况，考虑到各支车流的重要度不同，利用弧段阻尼系数调节不同车流的运输费用，确保重要车流能够优先通过。

在铁路网中，以总的运输费用最低为目标，构建基于改进点－弧模型的铁路网车流径路模型，即所有实际路段上的车流量与单位运输费用的乘积与虚拟路段上的车流量与虚拟路段上的单位运输费用的乘积之和最小，具体如下。

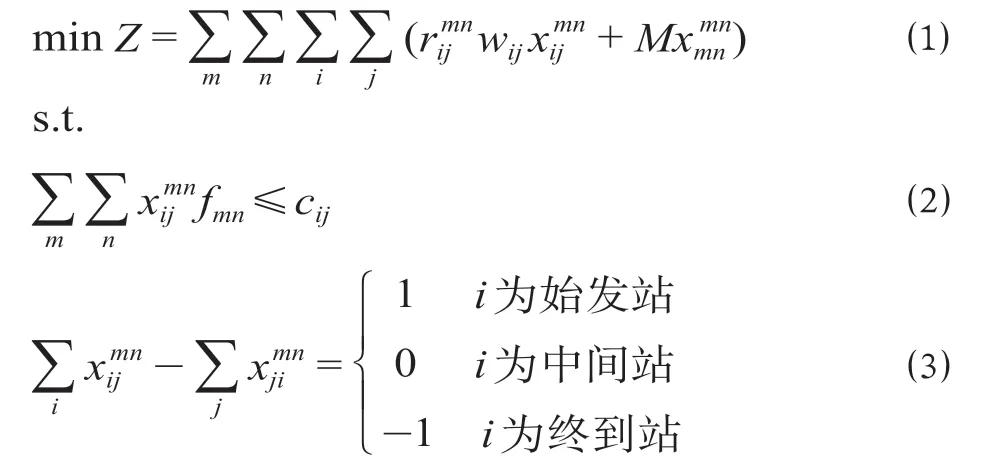
式中：Z为总运输费用；m，n，i，j为车站；fmn为从m到n的车流；为路段阻尼系数，表示车流fmn通过路段(i，j)时的阻尼系数；为0-1 决策变量，若车流fmn经过路段(i，j)，则xijmn取值为1，否则为0；M为一个很大的正数；为OD 对(m，n)之间的虚拟弧对应的指示变量，若该变量取值为1，代表车流fmn为不可行流，只能通过虚拟弧运送至终点，若取值为0，则代表车流fmn为可行流。

公式⑴为目标函数，表示最小化总运输费用(加权的广义费用)；公式 ⑵ 表示弧的能力约束，经过弧(i，j)的所有车流量必须小于弧(i，j)的能力；公式 ⑶ 表示节点流量守恒约束(共同径路约束)，同一车流fmn对于弧(i，j)，要么全部通过弧(i，j)，即= 1，要么全部不通过弧(i，j)，即= 0，解决了传统点－弧模型中弧的流量车流归属不清的局限性。

1.3 模型求解

基于改进点－弧模型的铁路网车流径路优化模型中决策变量是，该变量是0-1 变量，因而该模型为0-1 规划模型，且该模型的目标函数和约束条件都是线性的，可采用Lingo 软件进行求解，求解结果为所有的取值，对照铁路网中各个车站编号，即可得到各支车流是否通过各条路段，进一步将各支车流的连续的运行路段相连接，即可得到铁路网中各支车流的运行径路。

2 案例分析

以我国东北地区14 个车站及其弧段构成的局部铁路网为例，将各个铁路车站抽象为节点，将各个路段抽象为弧段采用基于改进点－弧模型的铁路网车流径路优化模型，路网结构示意图如图1 所示。为保证各个弧段都能通行车流，除了实际存在的弧段之外，建立虚拟弧段。

图1 路网结构示意图Fig.1 Railway network structure

2.1 基础数据

东北地区14 个车站之间有部分路段连接，各个路段的单位车流运输费用和年通过能力存在较大差异，部分路段通过能力较小，因而存在瓶颈路段。路段相关参数如表1 所示。不可行流的惩罚费用M取值1 000 元/车。

2019 年我国东北地区部分车站之间的年OD量在5 万 ～ 90 万t 之间。2019 年车流的年OD 量如表2 所示。对于部分年OD 量较大的车站，应尽量保证其选择单位运输费用较小的路段。在表2 中，OD 序号为1，7，9，11 的车流量较大，为重要车流，应选择单位运输费用较小的路段，可令路段阻尼系数为0.8，即保证重要车流以较低的费用通过弧段。

2.2 模型求解

利用Lingo 软件对构建的基于改进的点－弧模型的车流径路优化模型进行求解，可以得到车流径路优化方案如表3 所示。

由表3 分析可知，从大安北到梅河口车流的车流径路为虚拟弧大安北—梅河口，因而该车流为不可行流，从朝阳川到让湖路最短径路为朝阳川—吉林北—哈尔滨—让湖路，但是由于弧段能力限制，需要优先保证从朝阳川到白城的重要车流通过，因而从朝阳川到让湖路车流需要绕行朝阳川—牡丹江—哈尔滨—让湖路路径，而从朝阳川到白城的车流径路是最短径路。从求解结果可以看出，所有车流都满足不拆散的基本原理，起讫点相同的一支车流，或共同经过某一弧段，或均不经过该弧段。

将表3 中各支车流叠加到铁路网的各个弧段上，汇总得到东北部分铁路网的路段流量如表4 所示。

表1 路段相关参数Tab.1 Parameters of sections

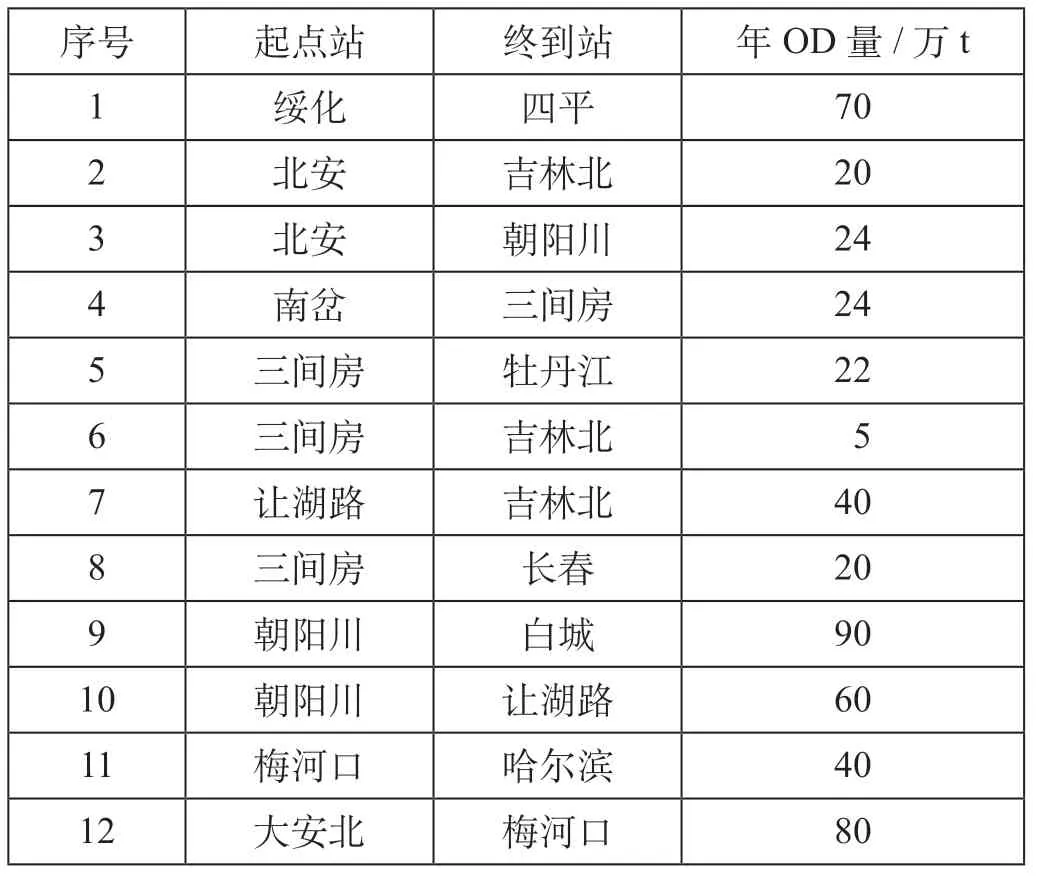
表2 2019 年车流的年OD 量Tab.2 OD train flow volume in 2019

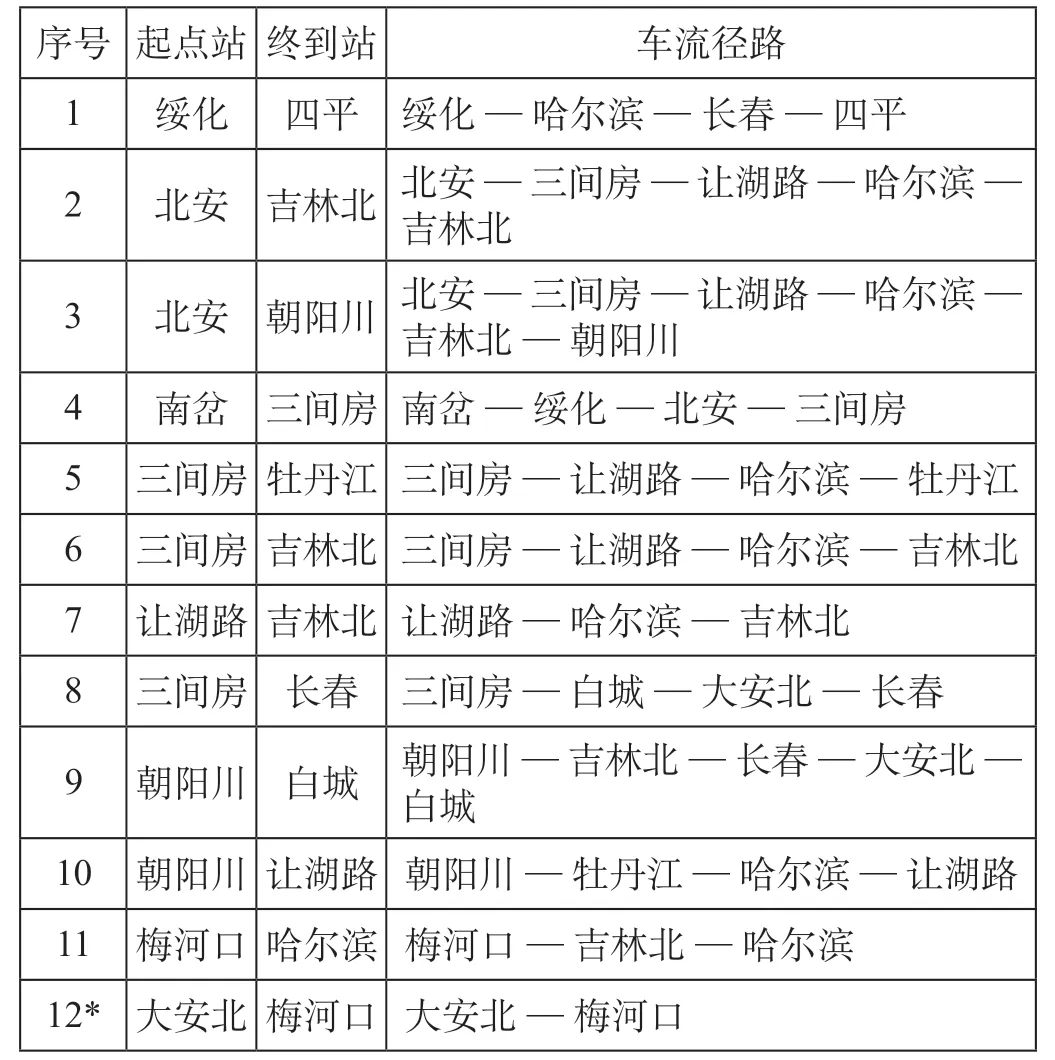
表3 车流径路优化方案Tab.3 Train flow route optimization plan

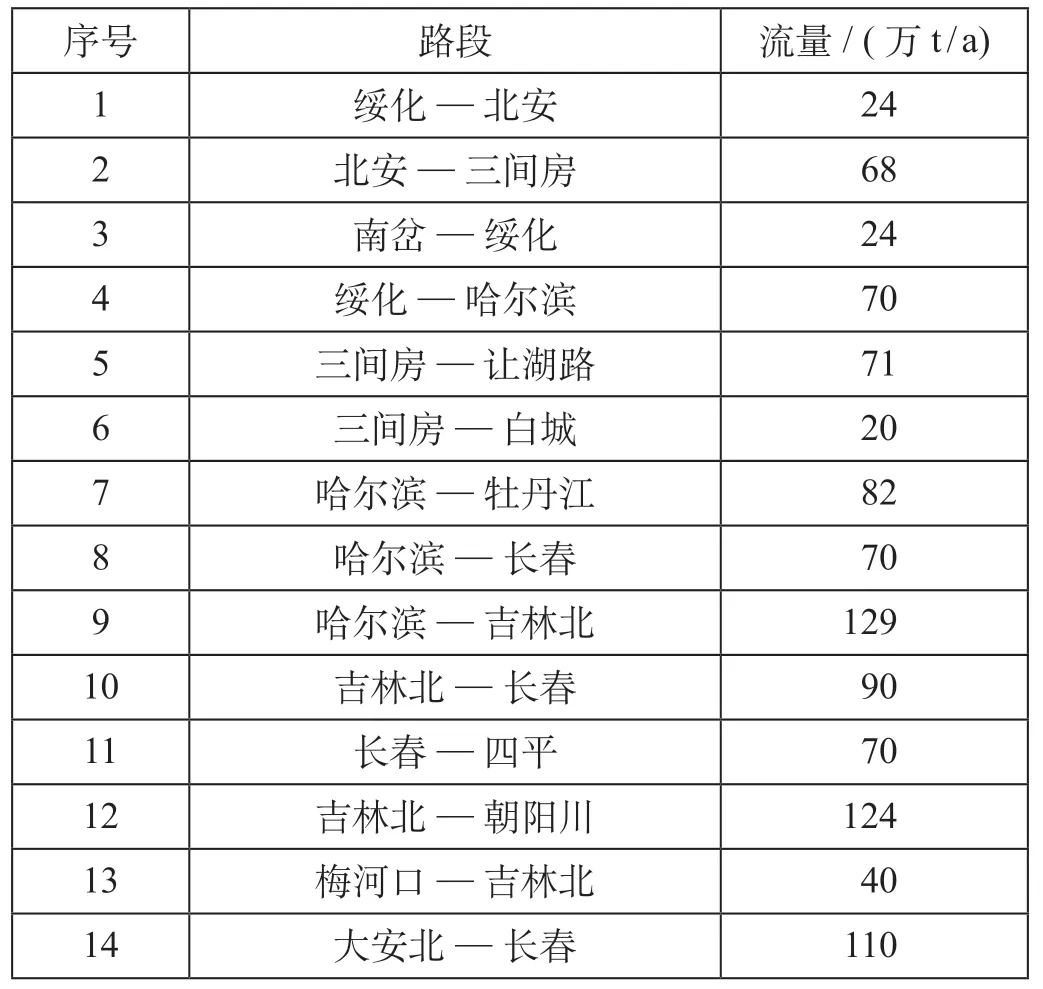
表4 东北部分铁路网的路段流量Tab.4 Flow of sections in Northeast China’s railway network

根据模型求解结果，不可行流为大安北到梅河口的车流，其余均为可行流，可行流的广义运输费用为6 106 元，不可行流的惩罚费用为80 000 元。模型结果表明，利用基于改进点－弧模型的铁路网车流径路模型可以准确快速地计算出可行流与不可行流的数量与费用，以及各支车流的运行径路，进一步验证了基于改进点－弧模型的铁路网车流径路模型的合理性与可行性。

3 结束语

车流径路的确定是铁路路网规划及铁路货物运输组织的重要工作之一，是车流组织工作的核心内容。车流径路优化对于降低路网车流运输费用，提高铁路运输部门的效率和效益意义重大。基于改进点－弧模型的铁路网车流径路模型，遵循各个车流在运行过程中不拆开的基本原理，能够准确定位各支车流的运行径路和不可行流的大小，在现实中具有较强的应用前景，尤其是在铁路网中各个车流重要度不同，路网瓶颈比较突出时更有效。今后应进一步深入研究在铁路网规模过大、基于中间节点的车流径路模型会产生过多的变量时的运算效率，以更好地满足铁路网车流径路优化需求。