基于时间窗和最低排空要求的集装箱空箱调运优化研究
胡剑鹏,罗 霞,甘易玄
(西南交通大学 交通运输与物流学院,四川 成都 611756)
0 引言
集装箱运输是实现“门到门”运输的一种高效率和高效益的运输方式,但铁路车站普遍存在集装箱发到不均的情况,为了避免空箱对流与闲置,需要采取科学合理的方法确定集装箱空箱调运方案。
目前,国内外学者对集装箱空箱调运的研究多集中于模型构建和算法的实现。在模型构建方面,主要研究主要体现在目标函数上,目标函数大致分为单目标和多目标2 种类型,单目标类主要包括单位时间内调运费用最小[1]、铁路运输利润最大[2]、乘客满意度最高[3]、空箱利用率最大[4]、供应链总服务成本最小[5];多目标类则由上述各项组合而成。在模型求解算法方面,主要分为针对线性规划模型的单纯形法和运输算法[1-2],以及针对非线性规划模型的遗传算法等启发式算法[3-4]。此外,为了深入探究空箱调运的特征,部分研究将运输网络分为确定性运输网络[2]和不确定性运输网络[6-7]2种,在空箱调运费用方面将其分为不考虑时间窗因素[1-2]和考虑时间窗的因素[7-8]2 类。蔡德伦等[9]还就空箱调运时的信息收集方法进行研究。
既有研究缺乏对空箱调运时优先满足站间最低排空要求目标的考虑,国内外集装箱空箱调运研究在计算效益时多关注于空箱调运的路径消耗费用,较少考虑空箱需求站时间窗造成的库存费用和机会损失费用。因此,应以最大化满足站间最低排空要求和最大化空箱调运收益为目标构建了双层规划模型,同时考虑供需关系约束和不同站点空箱输送能力约束。
1 基于时间窗和最低排空要求的集装箱空箱调运优化模型构建
站间最低排空要求是指为了规范铁路运输秩序,从而要求某些空箱供应站按照规定的排空数量与排空周期向某些需求站供应空箱的一种计划。在站间最低排空要求的基础上,考虑软时间窗导致的库存费用和机会损失费用,结合路网中的空箱供需关系进行空箱调运计划的制定,其中各站间各型箱的空箱调运数量为自变量,站间最低排空箱的满足数目与空箱输送效益为因变量,构建基于时间窗和最低排空要求的集装箱空箱调运优化模型。
1.1 模型假设
(1)可输送空箱的列车出发时间已由运行图固定且各站间的空箱发送费用已知。
(2)供应站与需求站间的最低排空要求已知。
(3)需求站存在1 个或多个对于集装箱需求旺盛即密集装车和发车的时间窗,在该有效时间窗内到达的货物不会因无法发出而产生库存费用和机会损失费用。
(4)需求站存在1 个或多个无效时间窗,在无效时间窗内到达的货物相对于邻近的后一有效时间窗会产生库存费用,相对于邻近的前一个有效时间窗会产生机会损失费用。j站1 天中的时间窗示意图如图1 所示,其中s表示第几个无效时间窗,s∈ 1,2,…,n;为j站第s个无效时间窗的起始时刻;为j站第s个无效时间窗的终止时刻。
1.2 模型构建
1.2.1 上层规划
(1)上层规划以站间最低排空箱的数目作为目标,计算公式为
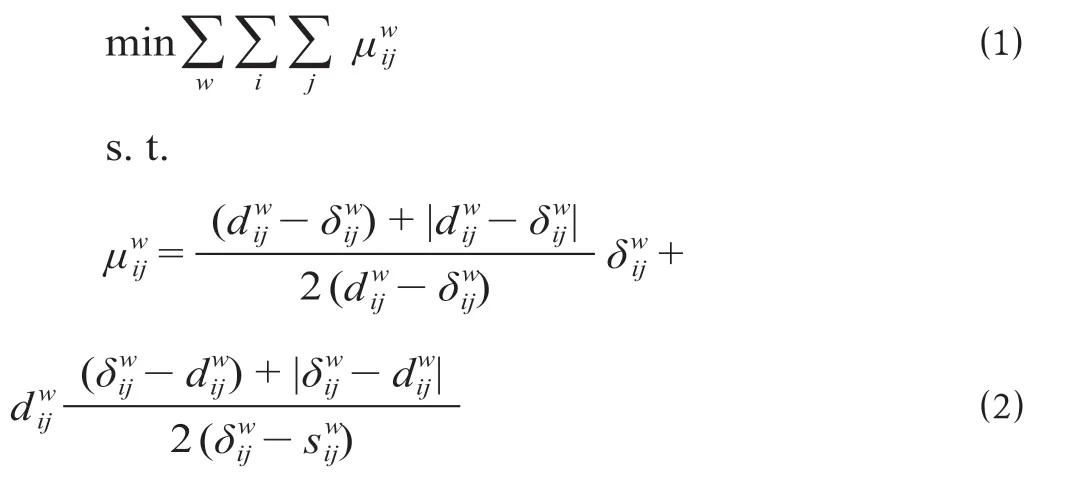

图 1 时间窗示意图Fig.1 Diagram of time window
式中:i为空箱供应站点;j为空箱需求站点;w为集装箱类型;为i站发往j站的w型集装箱中用于满足i站至j站间w型集装箱最低排空要求的部分;为i站发往j站的w型集装箱总数;为i站发往j站的w型集装箱的最低排空数量。
公式 ⑴ 表示站间最低排空箱发送总数;公式⑵ 表示由i站发往j站的w型空箱优先用于满足站间最低排空要求,即在>时供给j站的空箱中用于满足最低排空要求的w型集装箱数量为,在≤时供给j站的空箱中用于满足最低排空要求的w型集装箱数量为。
1.2.2 下层规划
(1)目标函数。下层规划以最大化空箱调运方案的总收益为目标,计算公式为
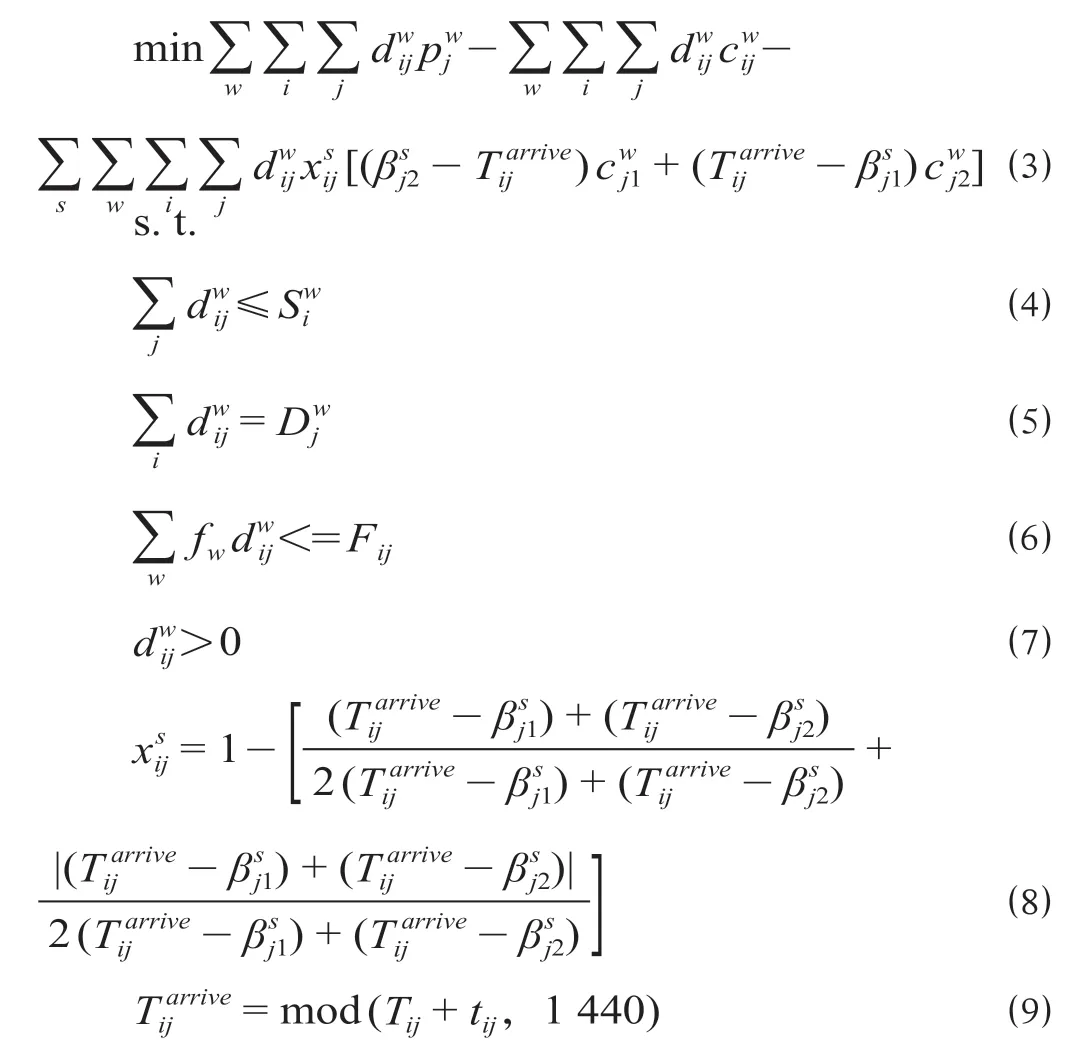
公式 ⑶ 表示空箱调运的效益,其中第1 项表示空箱到达需求站后由需求站装车发出所产生收益;第2 项表示空箱调运时产生的路径消耗费用;第3 项表示空箱在无效时间窗内到达时产生的库存费用与机会损失费用。公式 ⑷ 表示i站w型空箱的合计发送量不得超过i站既有的可供发送的w型空箱数目。公式 ⑸ 表示各供应站发往需求站j站的w型空箱数目总和应当等于j站对w型空箱的需求量。公式 ⑹ 表示由i站发往j站的集装箱换算数目不得超过i站与j站间线路空箱输送能力。公式 ⑺表示站间空箱输送数量应大于等于0。公式 ⑻ 表示当位于无效时间窗和之间时= 1,此时要考虑库存费用和时间费用,当不位于无效时间窗和之间时= 0,即不考虑库存费用和时间费用。需要注意的是,当无效时间窗跨天时,虽然位于无效时间窗内,但此时= 0,为了避免此种情况,在实际处理时若无效时间窗跨天如[23 : 00—2 : 00],则因将其看作2 个时间窗即[23 : 00—0 : 00]和[0 : 00—2 : 00],对应分钟制的[1 380—1 440]和[0—120]。公式 ⑼ 中取余数原因在于,如果Tij+tij> 1 440,则应当位于后一天的有效或无效时间窗,但研究中统一时间为1d,因而通过取余数将1 440 后到达的时刻转换为同一天内的时刻,使其与时间窗单位统一。
2 算法求解
该双层规划模型为非线性规划模型,无法利用Cplex 等求解器直接求解。因此,研究中将空箱调运过程分为以满足最大排空要求为目的进行的调运和以效益最大为目的进行的调运,并将后者转化为了容量限制下的最小费用最大流问题。记S,E为虚拟节点表起始点和终点,构建多品种网络图如图2 所示,括号内表示路段阻抗和路段最大容量,网络中虚拟起点至供应点,需求点至虚拟终点间阻抗均为0,为w型空箱在站点i→j的路段阻抗取值见公式 ⑽。虚拟起点与供应点间路段最大容量值为供应点的空箱供应数量,供应点与需求点间路段的最大容量值为i站和j站间空箱换算通过能力Fij,需求站与虚拟终点间路段的最大容量值为需求站j需要的w型空箱的总数。
为了令其与双层规划模型的目标一致,供应站与需求站间网络阻抗可表示为

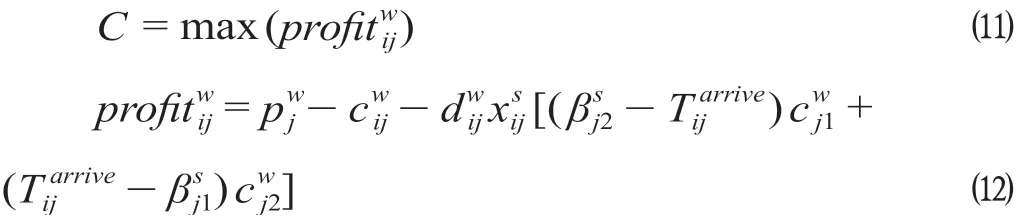
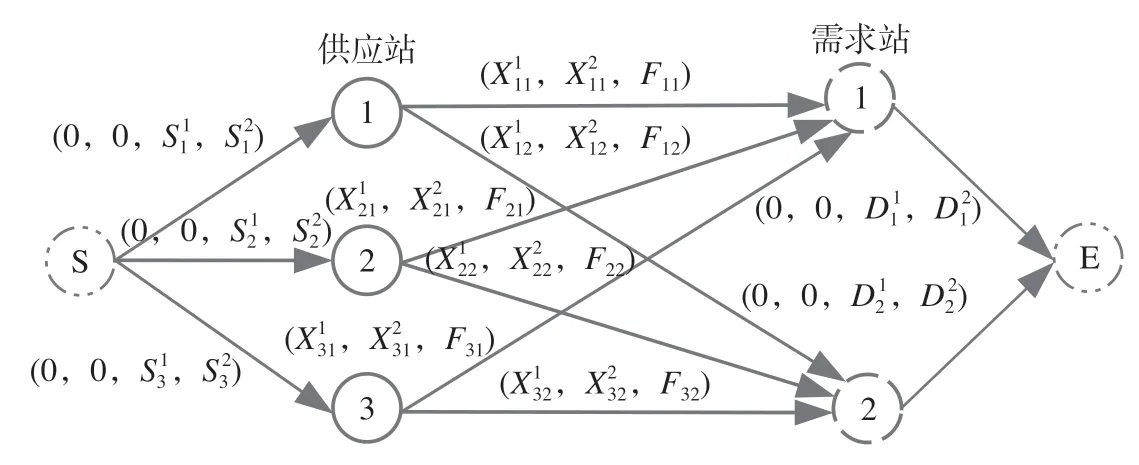
图2 多品种网络图Fig.2 Multi-commodity traffic network
式中:C是一个常数;为i→j站间w型空箱的输送利润。
不同站点间空箱输送效益越大路段阻抗就越小,结合最低排空要求扣除相应的供应量、需求量和站间容量后,可以将模型的求解转化为下式。
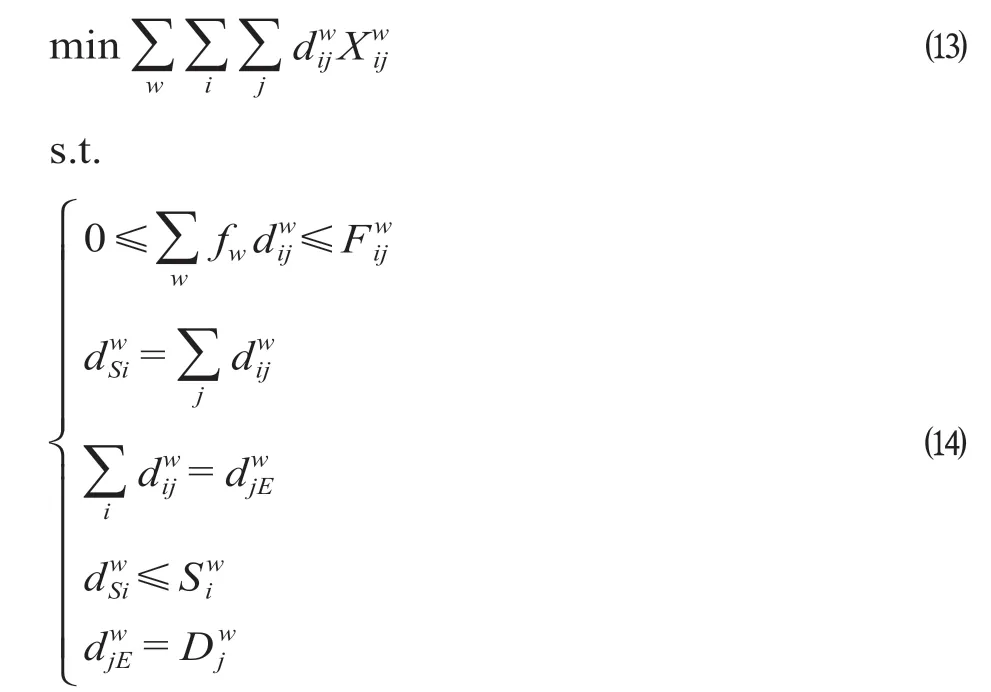
式中:为虚拟起点S与供应点i间w型空箱的输送数量;为需求点j与虚拟终点E间的w型空箱输送数量。
结合上层规划最优对网络进行调整后的模型为线性规划模型,可以用Cplex 进行求解,但该方法求解过程不直观,基于图论的配流方法更能准确的反映配流过程,因而针对下层规划模型,采用网络配流方法进行求解。
(1)以上层规划最优为目标的网络的调整方法。为了实现上层规划最优,对配流前的网络按下述步骤进行调整。
步骤1:空箱供应数量调整。从各供应站i的供应量中扣除用于满足站间最低排空要求的各型集装箱数量,计算公式为

步骤2:空箱需求数量调整。从需求站j中扣除由最低排空计划所满足的空箱需求数量,计算公式为

步骤3:站间最大空箱输送数量调整。从各站间线路通过能力Fij中扣除站间最低排空计划所占用的部分,计算公式为

上述步骤保证了站间最低排空计划的落实,实现了上层规划目标的最优。
(2)结合网络配流的下层规划求解方法。对调整后的新网络N按照下述步骤进行配流(以2 个箱型的空箱调运网络为例)。
步骤1:令初始k=1,利用Dijkstra 算法找出网络N中不同箱型在S,E间的最短路(Lw1,Lw2),选取min (Lw1,Lw2)对应箱型的最短路上进行流量分配,假设被选择路径为Lw1,每条路径上第2 个节点为供应站i第3 个节点为需求点j,则分配流量计算公式为
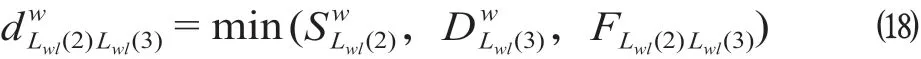
步骤2:更新被选中路径上的供应站空箱供应数量,需求站空箱需求数量和剩余可利用通过能力,更新方法如公式 ⒆ 所示,该更新方法可以保证站间分配流量满足供需约束和通过能力约束。
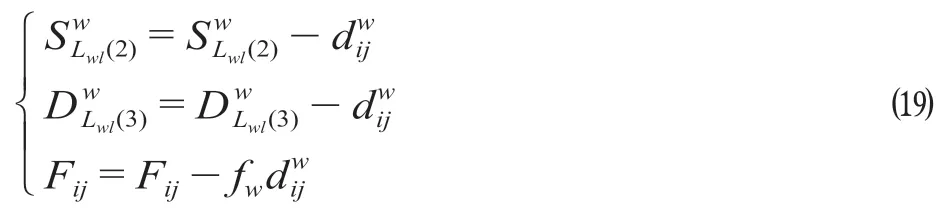
步骤3:更新被选择路径阻抗值,包括公式 ⒇ 中的3 种情形,通过此法可以避免在供应量耗尽、需求量全部满足或已达站间最大通过能力的路径上继续配流,从而避免了不可行空箱调运方案的产生。
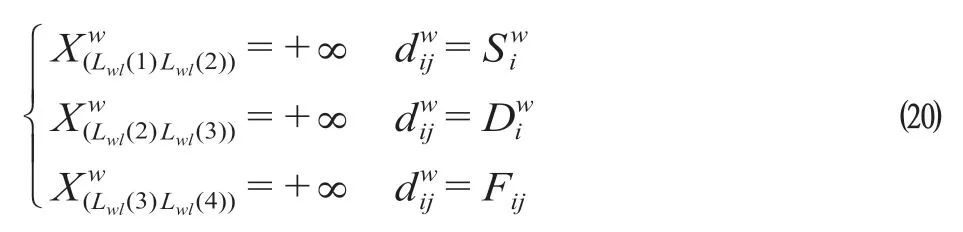
步骤4:由步骤3 得到阻抗更新后的网络N1,在新网络的基础上重复步骤1-3,直至或即供应量耗尽或需求量全部满足,求得一组可行方案plan和plan,可行方案形式如公式(21),表示第k次配流时w型空箱的配流方案。转至步骤5。
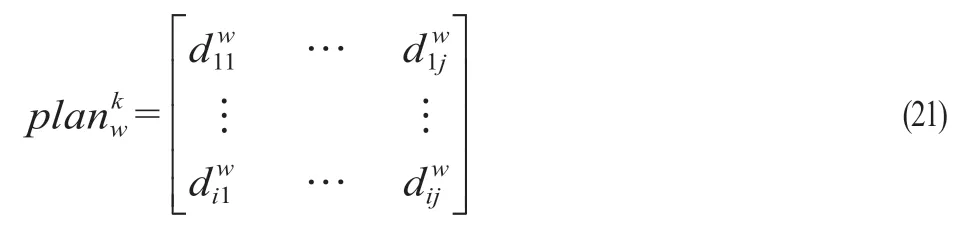
步骤5:利用BPR 阻抗函数公式将得到的可行方案plan和plan代入公式(22)更新阻抗,由网络N得到新的网络N2,需要说明的是生成网络N1的目的是求出一个可行方案,生成网络N2的目的是进行迭代寻优。
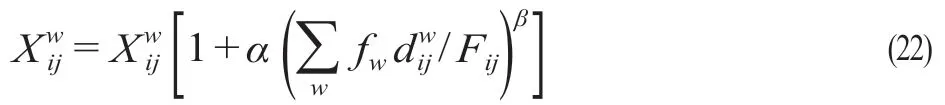
步骤6:按照公式(23)更新方案,,分别为第k- 1 次和第k次配流完成后迭代求和得到的w型空箱的配流方案,初始时∅。由的数值,判断是否满足收敛条件,满足则输出最优方案,否则k=k+ 1,并将N2作为步骤1的初始网络转至步骤1。
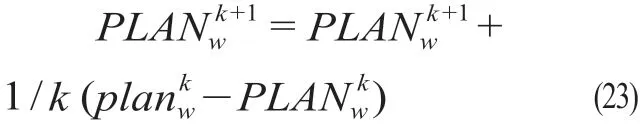
3 实例分析
研究选取了12 个空箱供应站,10 个空箱需求站以及20 TEU 和40 TEU2 种箱型进行模型及算法的验证。供应站点空箱供应数量如表1 所示,需求站空箱需求数量及发送效益如表2 所示,站间最低排空数量要求箱如表3 所示,空箱调运费用如表4 所示。
集装箱单位时间库存费用20 TEU 型箱取a,40 TEU 型箱取2a;机会损失费用20 TEU 型箱取2a,40 TEU 型箱取4a,取a 值为10 元/h-1[4]。20 TEU 型集装箱换算系数取f1= 1,40 TEU 型集装箱换算系数取f2= 2。配流方法求得的空箱调运方案如表5 所示。
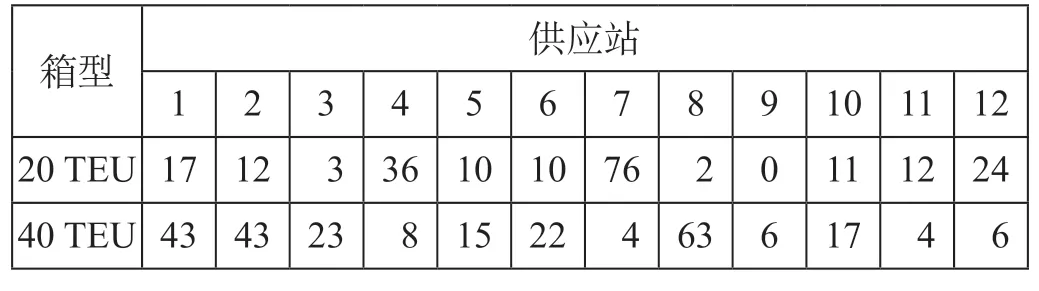
表1 供应站点空箱供应数量 箱Tab.1 Empty container supply quantity in supply stations
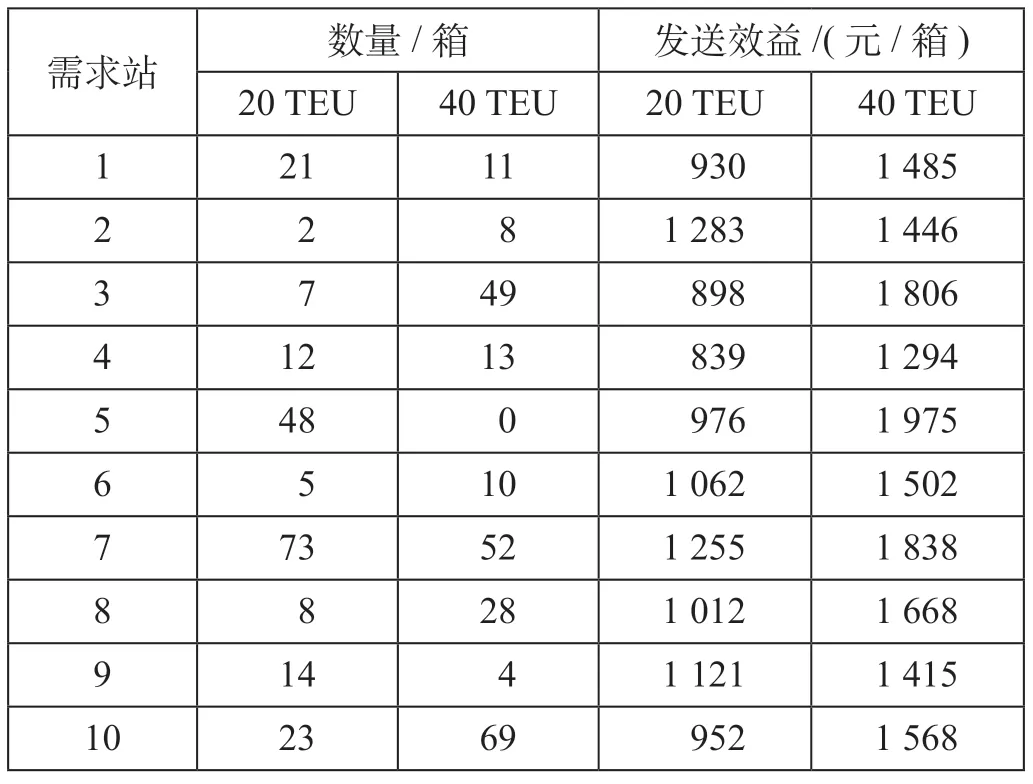
表2 需求站空箱需求数量及发送效益Tab.2 Empty container demand quantity in demand stations
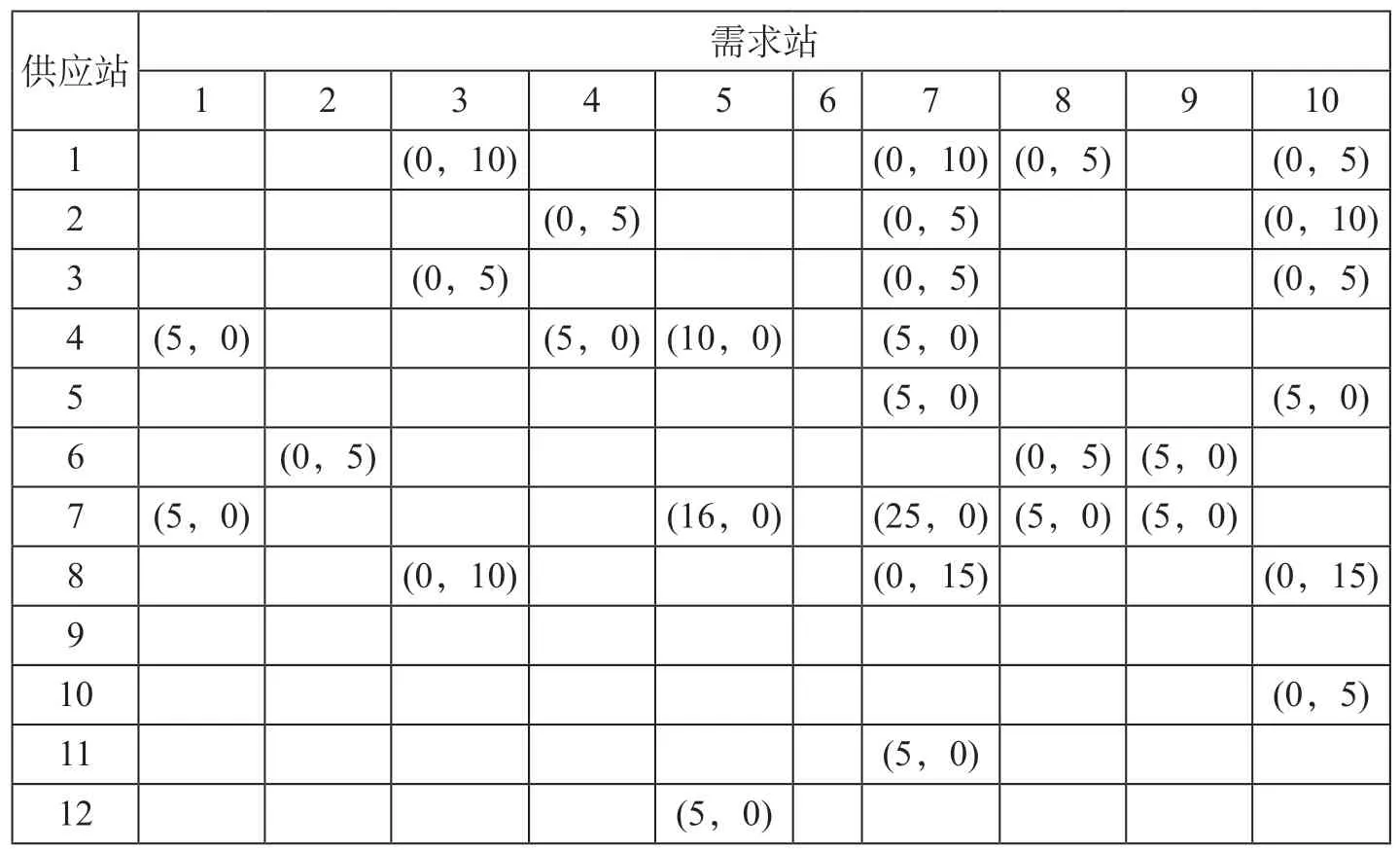
表3 站间最低排空数量要求 箱Tab.3 Minimum emptying container among stations
该最小费用最大流模型为线性规划模型,因而可以利用Cplex 加以求解,由Cplex 求得方案的效益值为425 412 元,由配流方法求得的空箱运输效益为415 832 元,配流方法求得效益为Cplex求得效益的97.75%,并且此时226 个站间最低排空箱数目均得到满足,说明该方法具备较强的可行性。
求得方案中存在站间最低排空要求的站点间的空箱输送存在2 种情况,一种是恰好满足(如站点1 →3,7 →5),此种情况产生是由于与其他路径相比该输送路径的运输费用较高,是以效益损失为代价来满足最低排空要求;一种为超量满足(如站点1 →7),此时该路径的运输费用低,选择该路径不仅可以满足站间最低排空要求也能提高空箱调运收益。因此,可以认为该模型较好地兼顾了空箱调运的运输秩序与运输效益。
不同a值下的空箱输送效益如图3 表示,可以看出随着a值的增大,空箱输送效益不断减小,并且排空优先条件下求得的效益与仅考虑效益条件下求得的效益之间的差值不断缩小,即为满足最低排空要求所付出的效益损失代价随时间窗对应库存费用和机会损失费用的增大而减少。
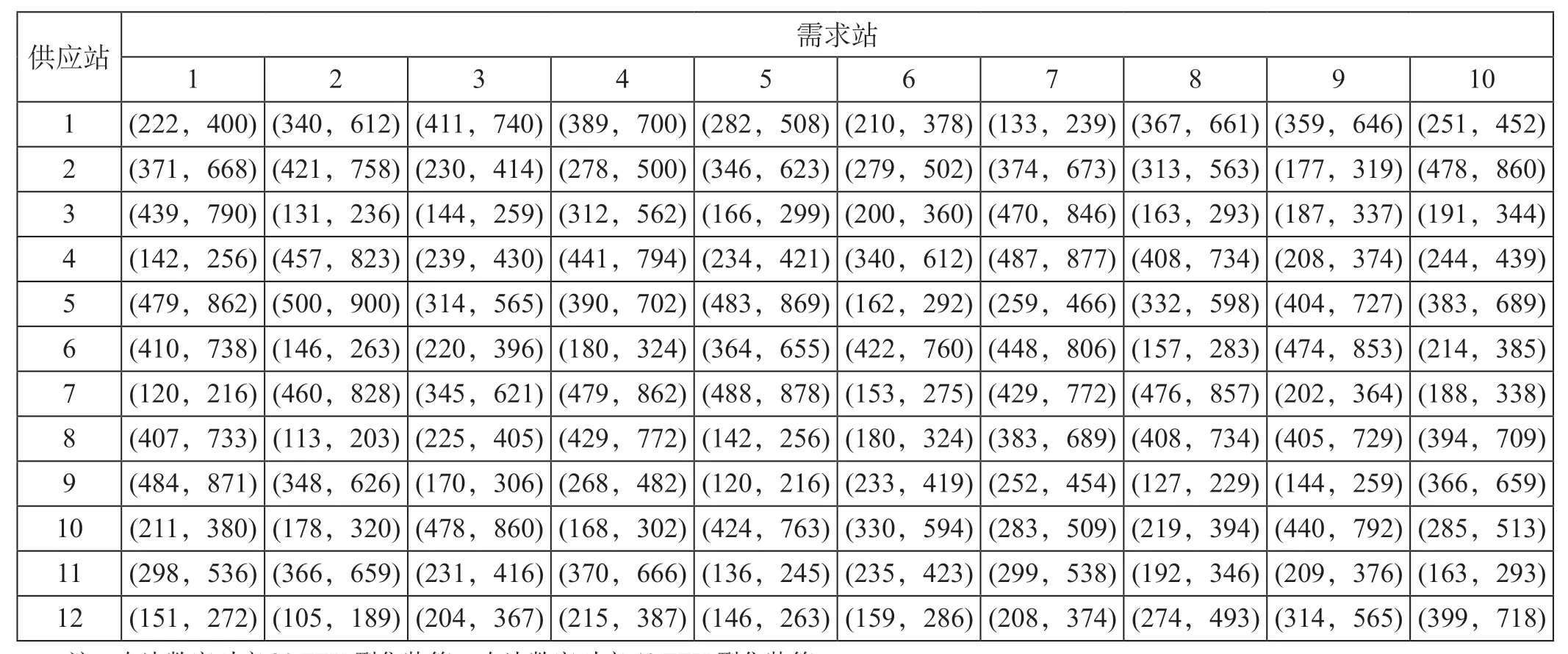
表4 空箱调运费用 元/箱Tab.4 Empty container transfer cost
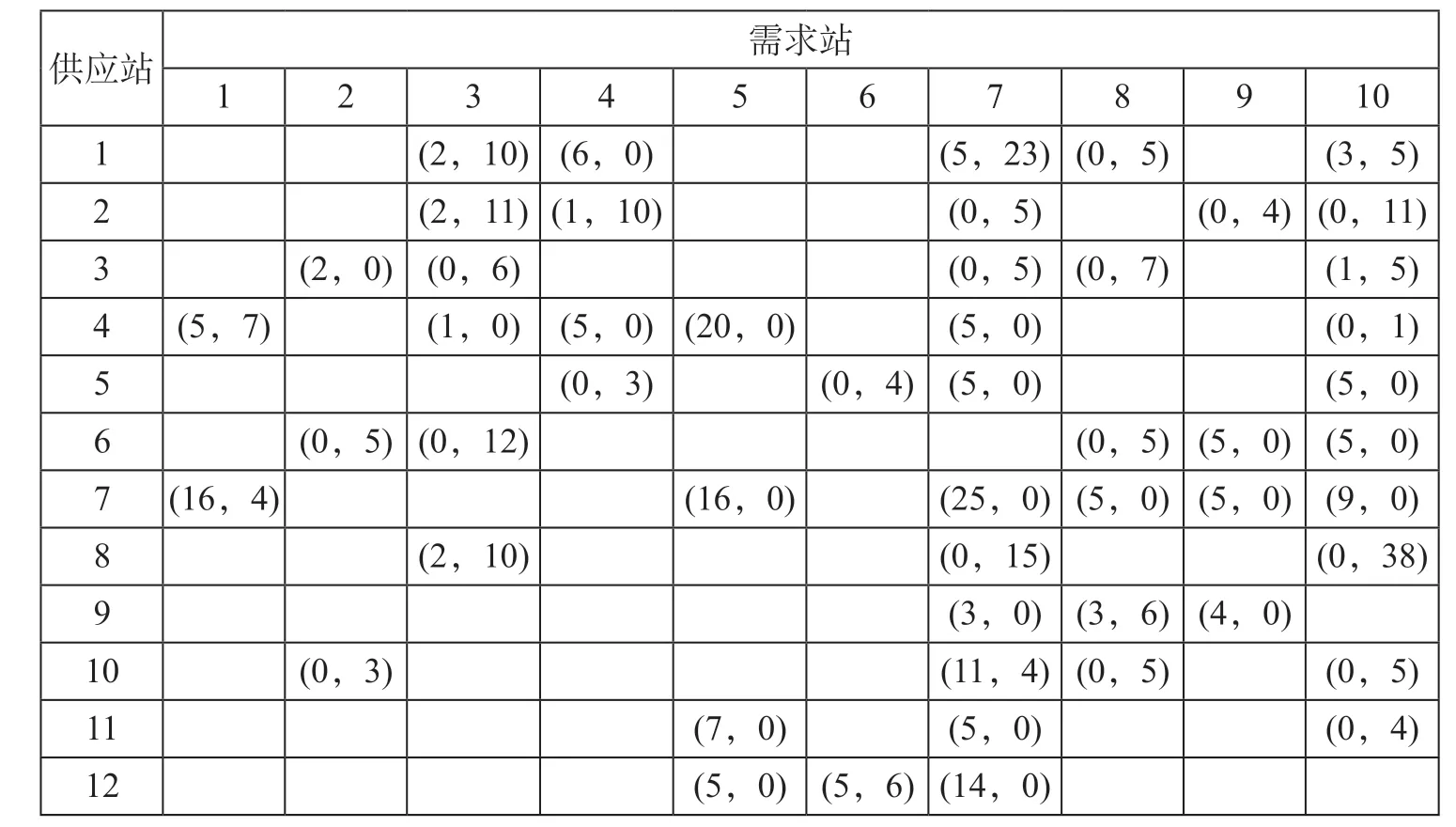
表5 配流方法求得的空箱调运方案 箱Tab.5 Container transfer plan by flow distribution method
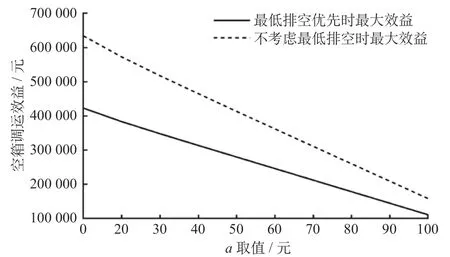
图3 不同a 值下的空箱输送效益Fig.3 Benefits of empty container transfer at different values of a
4 研究结论
为了兼顾空箱调运效益和铁路运输秩序,研究中考虑了时间窗费用和站间最低排空需求并构建了双层规划模型以解决空箱调运优化问题。针对建立模型非线性的性质,将调运过程划分为了以满足最大排空要求为目的进行的调运和以效益最大为目的进行的调运,将后者转化为了容量限制条件下的最小费用最大流问题并设计了相应算法,主要研究结论如下。
(1)利用设计算法对该空箱调运问题进行求解时,算法求得效益值为由Cplex 求得最佳效益值的97.75%,说明配流方法在寻找空箱调运问题的全局最优解时具备较佳的应用效果。
(2)求得方案中站间最低排空要求存在恰好满足和超量满足2 种情形,恰好满足时是以效益损失为代价来满足最低排空需求,超量满足时则说明该供应方式不仅有利于满足站间最低排空要求还有助于提高输送效益。说明所得方案是在保证空箱调运秩序的基础上实现的效益最大化。
(3)需求站无效时间窗内单位时间库存费用和机会损失费用的变化对空箱调运的效益有显著影响,为满足最低排空要求所付出的效益损失代价随时间窗内库存费用和机会损失费用的增大而减小。

