关于一个条件对称不等式的研讨
2022-06-27 06:41安徽师范大学数学与统计学院于洪翔郭要红邮编241000
中学数学教学 2022年3期
安徽师范大学数学与统计学院 于洪翔 卢 尧 郭要红 (邮编:241000)
1 引言
《数学通报》2021 年第5 期问题2604 是一个条件对称不等式问题.
问题2604[1]已知a、b、c>0,且abc=1.


对该问题进行研讨,我们得到以下结论.
命题 已知a、b、c>0,且abc=1,若0 <λ≤8 . 则有
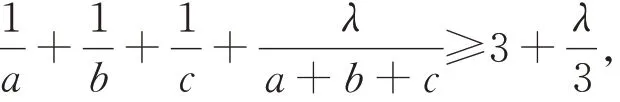
等号当且仅当a=b=c=1 时成立.
2 主要结论的证明

运用拉格朗日乘数法,作拉格朗日函数:
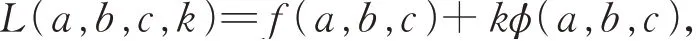
其中k为拉格朗日乘数.
对L求偏导数,并令它们都等于0,则有
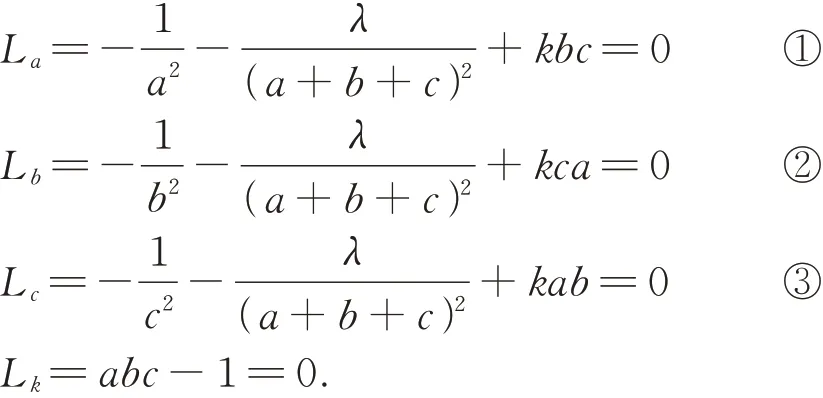
④由①、②、④得


若a-b=0,b-c=0,c-a=0 都 不 成立,即a-b≠0,b-c≠0,c-a≠0,由⑤、⑥、⑦得a-b=0,b-c=0,c-a=0,矛盾.
若a-b=0,b-c=0,c-a=0 有 且 仅 有一个成立,不妨设b-c=0,a-b≠0,由⑤式知,

方程⑧的根的判别式Δ=(4-λ)2-4×4=λ2-8λ.
(Ⅰ)当0 <λ<8 时,则Δ=λ2-8λ<0,方程⑧无解,所以L(a,b,c,k)只有唯一一个稳定点

等号当且仅当a=b=c=1 时成立.
命题得证.
3 讨论
3.1 文[2]另一个结论的否定
由上述证明过程知,L(a,b,c,k)的稳定点的三个坐标a、b、c不可能两两不等,所以,文[2]中的另一个结论“当λ>9 时,不等式

L(a,b,c,k) 的7 个 稳 定 点 处,哪 一 个 是f(a,b,c)的 最 小 值 点,f(a,b,c)的 最 小 值 是 多少?是一个计算量颇大、值得继续研究的问题.我们将此问题作为擂题(141),期待能获得解决.
猜你喜欢
语数外学习·初中版(2022年4期)2022-06-10
中等数学(2020年7期)2020-11-26
安徽师范大学学报(人文社会科学版)(2020年1期)2020-02-23
杂文选刊(2019年12期)2019-12-06
新青年(2018年8期)2018-08-18
安徽师范大学学报(人文社会科学版)(2018年4期)2018-07-09
幸福·婚姻版(2018年12期)2018-02-22
校园英语·下旬(2018年10期)2018-01-05
中学生数理化·中考版(2016年8期)2016-12-07
太空探索(2014年3期)2014-07-10

