发展“数学抽象”素养的五种策略——基于SOLO 分类理论视角

浙江师范大学教师教育学院 刘绿芹 （邮编：321004）

江苏省建湖高级中学 杨海涛 （邮编：224700）

当前，《普通高中数学课程标准（2017 年版2020 年修订）》已进入实施阶段，课程标准提出了数学学科核心素养，包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析[1]. 这些核心素养将在数学学习的过程中一步步地形成和发展. 为此，现基于SOLO 分类理论，从五个方面就数学核心素养中的“数学抽象”素养的形成与提升进行策略探究.

1 “数学抽象”素养与SOLO 分类理论

1.1 数学抽象

“数学抽象”素养是高中数学六大核心素养之一，其主要内容为：通过对数量关系与空间形式的抽象，得到数学研究对象的素养. 包括：从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系，从事物的具体背景中抽象出一般规律和结构，并且用数学语言予以表征[1].在江苏《高考说明》中，将抽象概括作为一种数学基本能力，其考查的要求是：能够通过对实例的探究，发现研究对象的本质；能够从给定的信息材料中概括出一些结论，并能将其应用于解决问题或作出判断[2]. 由此可见，数学抽象在高中数学中的重要性，高中阶段如何形成与提升“数学抽象”素养则成了一个避不开的话题.

1.2 SOLO 分类理论

SOLO 分类理论是香港大学教育心理学教授比格斯（J.B.Biggs）首创的一种学生学业评价方法.“SOLO”是英文“Strucre of the Observed Learning Outcome”的缩写，其意为可观察的学习结果的结构[2]. 该理论是一种以等级描述为特征质性评价方法. 比格斯把学生对某个问题的学习结果由低到高划分为5 个层次：前结构水平（P）、单一结构水平（U）、多元结构水平（M）、关联水平（R）、扩展抽象水平（E）. 由此可见，通过努力，学生的“数学抽象”素养可以从前结构水平逐步提升至扩展抽象水平.

1.3 两者之间的相互关系

“数学抽象”素养的发展往往呈现出螺旋上升的层级结构，在SOLO 分类理论的视角下，根据学生“数学抽象”素养的形成与发展结果，可以将“数学抽象”素养分为五个层次水平，不同层次的“数学抽象”素养水平对应不同的SOLO 层次水平，每一层次水平则对应着不同的提升策略. 在相应策略的作用下，学生“数学抽象”素养得到形成与发展，进而升至高一级层次水平.SOLO 分类理论是“数学抽象”素养提升的有效监测工具，“数学抽象”素养是施行SOLO 分类理论的载体.

在新版课程标准中，数学学科核心素养水平被划分为三个水平层次：水平一、水平二、水平三，从划分标准可以看出，学生形成核心素养水平需要具有一定基本知识与技能，即建立在单一结构水平（U）之上，水平一则对应着多元结构水平（M），水平二则对应着关联水平（R），水平三则对应着扩展抽象水平（E）.

2 形成与提升“数学抽象”素养的策略

数学抽象素养的形成伴随着学生的认知水平的提升，在前结构水平，学生几乎没有“数学抽象”素养，在单一结构水平阶段，学生只是具有单一、分散的基础知识与技能，“数学抽象”素养较低，但要形成“数学抽象”素养水平则需要学生具备这些基本知识与基本基本技能. 因此，形成与发展“数学抽象”素养的基本要求是：跳出前结构水平，重视单一结构水平；发展“数学抽象”素养的基本要求是延伸多元结构水平，提升关联水平，最终形成扩展抽象水平.

数列是按照一定次序排列的数，体现数量与数量之间的关系，高中数列的问题是体现“数学抽象”重要载体之一. 为了深入说明形成与提升素养水平策略，现结合一道高中数列问题，通过对多个学生的解题过程进行分析，探求形成与提升“数学抽象”素养的具体操作策略.

例题如下：已知数列{an} ，对于任意n≥2，在an－1与an之间插入n个数，构成的新数列{bn} 成等差数列，并记an－1,x1,…,xn,an这n+2 个数均值为Cn－1.（1）若在（1）的条件下，证明为等差数列.

2.1 跳出前结构水平

前结构水平（Prestructural）：学生并没有真正理解学习内容，只能够提供一些逻辑混乱，没有论据支撑的答案，或被以前所学的无关知识困扰，找不到任何解决问题的办法.

形成“数学抽象”素养的首要问题是必须要跳出前结构问题，避免被无关的内容困扰. 这就需要加强对基本概念、定理、公理等内容的真正理解，理清其中的基本关系. 同时，能够将两种或多种类似的学习内容进行区分与辨别，形成清晰的基本知识架构.

【学生1 解题片段】

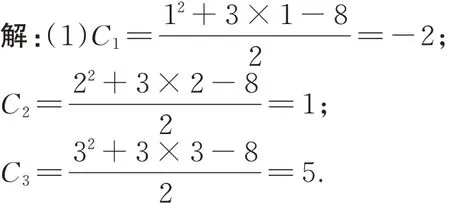
评析从学生的解题过程来看，该生未能理解题目的内容，且未能真正理解“通项”的含义，混淆了Cn与an，所答内容没有逻辑支撑，没有找到解决该题的办法. 依据SOLO 分类理论，此认知水平属于前结构水平. 该生需要通过对数列通项的基本知识的再学习，理解an的真正含义，同时还需要对等差数列的基本知识进行再学习.

作为教师，面对前结构水平的学生时，应当提前为学生准备好问题中用到的基本知识，教学策略上，可以是“提问检查”的方式，可以是“引导复习”的方式，也可以“小题练习”的方式. 总之，通过“预备知识”的方法，让该层次的学生在解决问题前，能够掌握问题中用到的基本知识，从而避免所答内容无效，打击学生继续学习的信心.

2.2 重视单一结构水平

单一结构水平（Unistructural）：学生根据相关知识，找到了一个解决问题的办法、思路，但却就此收敛，有时单凭一点论据就跳到答案上去.

形成“数学抽象”素养需要特别重视单一结构水平，该层次水平属于承上启下阶段，相关知识积累的越多则越能向多元结构水平发展，反之则会回到前结构水平. 在此过程中，学生的思维由显现思维向隐形思维逐步发展，“数学抽象”素养正在从这个阶段慢慢形成.

【学生2 解题片段】

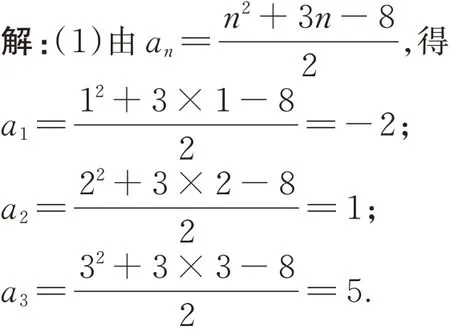
由题意，设插入的n个数分别为x1，x2，…xn，则an－1，x1，x2，…，xn，an成 等 差 数 列，此 时 有x1－an－1=x2－x1=…=an－xn=d.

同 时，an－1,x1,…,xn,an这n+2 个 数 均 值 为Cn－1，则有

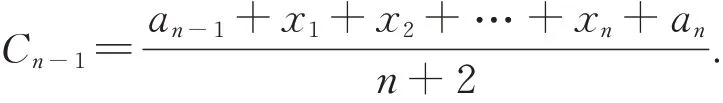
评析从学生2 的解题过程来看，该生利用已有的数列知识，将将题目中的三个主要条件都往下进行了一步，形成了三个思路、方向. 这说明，该生具备数列的基本知识，能够掌握数列的通项的含义及等差数列的内涵，也理解了题目的含义，但并未能将问题继续探索下去. 依据SOLO 分类理论，此认知水平处于单一结构水平. 当学生想到在在an－1与an之间插入x1，x2，…xn时，教师可以追问若插入的n=2 时，构成什么样的数列？此时C1是多少呢？若n=3 呢？n=4 呢？n=5 呢？则第（1）问不难解决.

作为教师，要特别关注处于单一结构水平的学生，这部分学生具有一定数学基本知识，教师在平时的教学过程中，应有意识地进行“引导式追问”教学，让学生的思维在不断的引导、追问下得到发展，“数学抽象”的素养也正是在这样的过程中逐步形成，为认知水平的进一步提升打下基础.

2.3 延伸多元结构水平

多元结构水平（Multistructural）：学生找到了构成问题越来越多的、正确的相关特征，并找到了多个解决问题的思路，但学生只是简单罗列这些特征、思路，还不具有将它们有机整合的能力.

提升“数学抽象”素养需要延伸学生多元结构水平，引导学生利用已经总结出来的多个思路，将现有的规律、特征进行整合提升，以便解决更加抽象的问题，进一步提升认知水平.

【学生3 解题片段】

解：（1）由得a1=－2，a2=1，a3=5，a4=10，则在a1与a2插入两个数：－1、0，使得－2，－1，0，1 成等差数列，此时，均值

在a2与a3插 入 三 个 数：2、3、4，使 得1，2，3，4，5 成等差数列，此时，均值C2=3；

在a3与a4插 入 四 个 数：6、7、8、9，使 得5、6、7、8、9、10 成 等 差 数 列，此 时，均 值

(2)由第一问中的规律知，在an－1与an之间插入n个数成等差数列，则构成的新数列{bn} 的公差设 插 入 的n个 数 为x1，x2，…xn，则

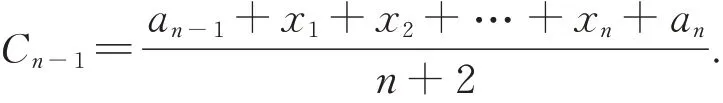
评析从学生3 的解答过程来看，首先，该生能够从将n=1，n=2，n=3，n=4 逐个代入，求出a1=－2，a2=1，a3=5，a4=10，则说明该生能够理解了“通项”的真正含义. 其次，该生在“a1与a2间”，“a2与a3间”和“a3与a4间”分 别 插 入“－1、0”，“2、3、4”和“6、7、8、9”，进而求 出 了 均 值C1、C2和C3，则说明该生找到了解题的基本方向，并能正确运用等差数列的知识罗列出具体的等差数列，解决了第一问. 最后，该生还从形成的三个具体等差数列中，抽象出新数列{bn} 的公差为1. 然而，学生并没有能够进一步整合并抽象““插入两个数、插入三个数、插入四个数”及“公差d”这些规律特征，导致第二问无法解决. 根据SOLO 分类理论，此认知水平为多元结构水平.教师教学上，应让学生尝试从插入“两、三、四个数”，转变为“插入n个数会得到什么？”的角度思考，此时学生会发现x1，x2，…xn无法处理，题目的难度突然增加，导致解题无法进行下去. 此时，教师再让学生尝试从“怎么求均值”的角度，跳过“插入n个数会得到什么”问题，结合C1、C2、C3的求法，学生不难找出均值的求解办法.

作为教师，应当对学生的各种思路进行“试走式”教学探究，从多角度引导学生进行探究，鼓励学生不惧困难，不怕失败，要从“不通”的思路中提升能力. 通过类似于这样的“试走式”尝试，学生的多元结构水平将得到延伸，“数学抽象”素养则能得到了进一步发展.

2.4 提升关联水平

关联水平（Relational）：学生会整合各部分内容而使其成为一个有机整体，表现为能回答或解决较为复杂的具体问题，能将多个思路结合起来思考.

提升“数学抽象”素养中最关键的，也是最难的一步是提升关联水平，此阶段的学生已具有一定的数学抽象素养，抽象思维能力也较强，能够解决一些较为复杂的问题. 然而，若要进一步达成扩展抽象水平，则需要进一步提升关联水平.

【学生4 解题片段】

例析从整体上看，该题的难度属于中等，其难度主要体现在数列的转换上，从{an}到{bn}，再到{Cn}，然后又到{Cn+1－Cn}、{dn}，这就需要学生有很好的抽象思维能力. 从学生4 的解答过程来看，该生能基本解决该题，能够将多种数列知识相关联，并且能够构建新的数列. 根据SOLO 分类理论，此认知水平处于关联水平. 此时，教师还可以根据学生的学习力，进一步提升思维层次要求，让学生在该题的基础上，自行编制新问题.

作为教师，针对关联水平阶段的学生，教师可以尝试进行“命题式”探讨教学，让学生间以某内容为背景，在已有的问题背景上，编制新的问题，同学间互相命题，交叉答题，并互相探讨. 这将学生思维得到进一步发散，创新意识得到加强，提出问题，分析问题和解决问题的能力也得到进一步提高.

2.5 形成扩展抽象水平

扩展抽象水平（Extended Abstract）：学生能够对问题进行抽象概括，并从理论的高度分析问题，从而使问题深化，并得到拓展. 这代表着一种更高水平的学习能力，这一水平的学生表现出更强的钻研和创造意识. 当学生形成扩展抽象水平，则说明学生的“数学抽象”素养已经达到了较高的水平，具有“跳出问题看问题”的能力，这正是高中数学教学的理想目标.

学生5，学生6 在已经解决了该题的基础上，开始提出新的设想：

【学生5 的设想】

在（1）的条件下，{Cn}是等差数列吗？

学生间互相讨论后，验证：Cn+1－Cn=是等差数列.【学生6 的设想】

在（1）的条件下，除了λ=1 外，还有没有其他常数λ，使{Cn+1－λCn}是等差数列？

学生间互相讨论后，验证：假设{Cn+1－λCn}成 等 差 数 列，则 有（Cn+1－λCn）－（Cn－λCn－1）是 常 数. 根 据 题 意 可 得，（Cn+1－λCn）－（Cn－故当1－λ=0，即λ=1 时，假设成立. 因此，只有常数λ=1，使得是等差数列.

评析从学生的设想与验证来看，特别是学生6，已经深刻掌握了该题的本质，并且对题目进行扩展探索，这说明学生不仅掌握了该问题，还能够进行问题的拓展与发散，学生的“扩展抽象水平”正是在这样的过程中逐步达成.

作为教师，应当在课堂上引导学生进行“再来一问”的探索性尝试，并让学生进行头脑风暴，提出各种不同见解的问题. 同时，鼓励学生对其给出的各种假设、设想，进行验证与证明，在此过程中，教师要与学生一起，不断点拨学生，引导学生，激励学生，进而形成更有价值的内容，建立起学生专研数学、创造数学的信心.