定比点差法妙解解析几何问题

浙江省宁波市镇海中学 虞哲骏 （邮编：315200）

点差法在处理中点问题的时侯往往能够大大简化计算，它是每一个学生都必须掌握的一个方法．但在实际解题过程中我们碰到的往往都不是线段AB的中点这么筒单，但是只要是同一条直线上的点都可以利用向量的比例来求得它们的坐标关系，这类问题称之为定比分点问题．作为处理定比分点问题的主要方法，点差法的升级版“定比点差法”便应运而生了．

1 定比分点的坐标公式

设A(x1，y1)，B(x2，y2)，P(x0，y0)，利 用 向 量的线性关系不难求出：

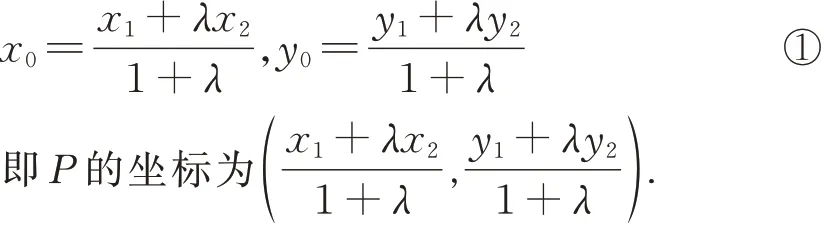
①式便是定比分点公式. 显然当λ=1 时，定比分点公式就变成了中点坐标公式，这也说明了中点坐标公式是定比分点的一种特殊情况．

2 基本步骤

本命题的逆命题也成立，同时此结论与极点极线有着紧密的联系．相对于常规解法，定比差法在处理定比分点问题细化下的三点共线，相交弦，定点问题，比例问题等均具有较明显的优势．

为了更加了解定比点差的妙处，通过几个典型问题来加以实践吧．

3 实战应用

（1）三点共线问题

（2018 浙江）已知点P(0，1)，椭 圆上两点A、B，满足，则 当时，点B横坐标的绝对值最大．

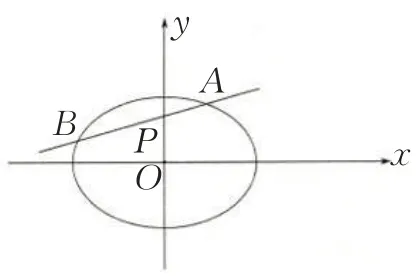
图1

解析设A(x1，y1)，B(x2，y2)，由由定比分点坐标公式得：

将A、B代入到椭圆方程得：

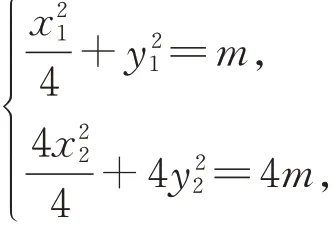
故当m=5 时，点B的横坐标的绝对值最大．

（2）定值问题

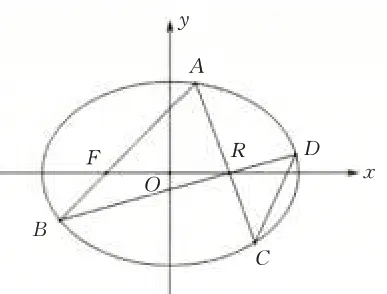
图2

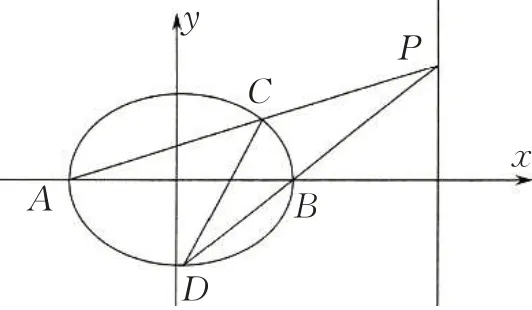
图3

（3）定点问题

（2020 年 全 国一卷理节选）已知A、B分别为椭圆E:的左、右顶点，P为直线x=6 上的动点，PA与E的另一交点为C，PB与E的另一交点为D．证明：直线CD过定点．

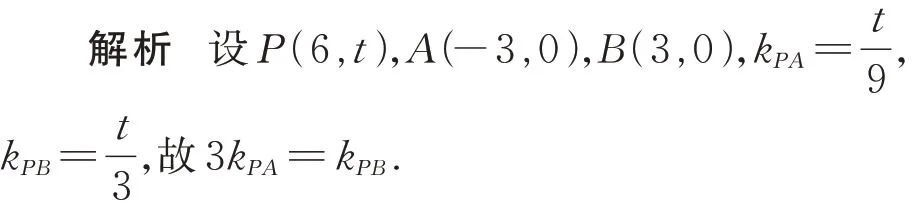
由椭圆对称性可知：若CD过定点，则定点坐标必在x轴上，并设定点为T(m，0)．

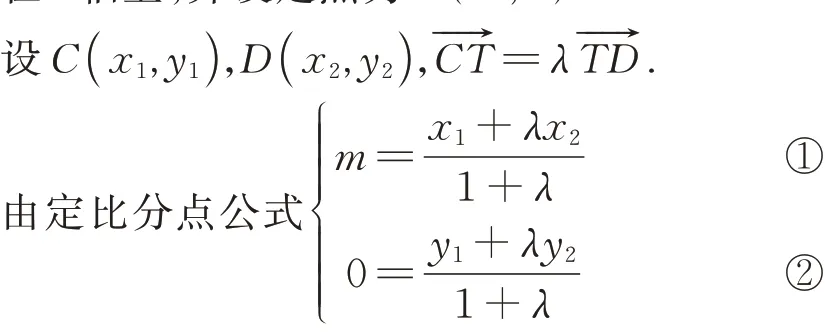
将C、D两点代入椭圆方程可得

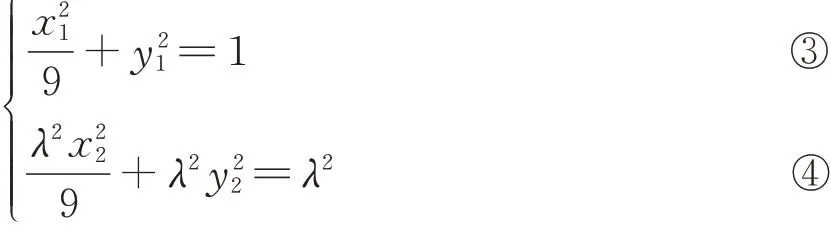
由④③作差整理可得：

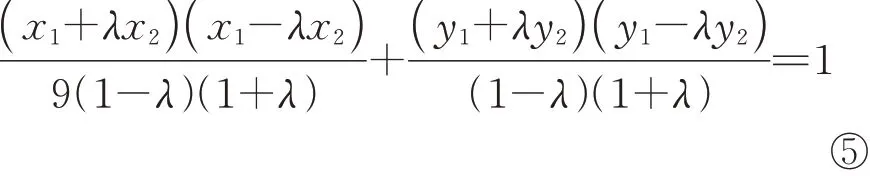
将①②代入到⑤中，整理可得：mx1－mλx2=9－9λ．

和①联立得到

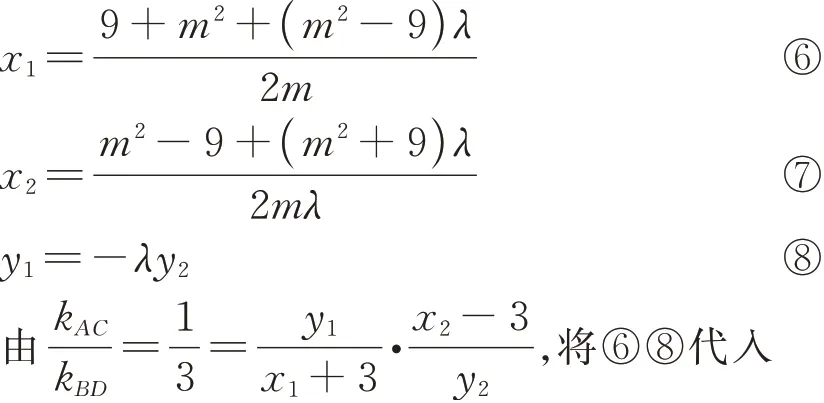
整理得2m2+3m－9+(2m2－9m+9)λ=0，

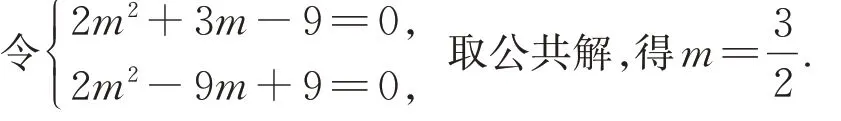
故恒过定点坐标

（4）定线问题

（2021 年 浙 江模拟）如图4，已知抛物线y2=2x，过点P(1，0) 作 两 条直线分别交抛物线于A、B和C、D，直线AC、BD交 于 点Q，求证：Q在定直线上．

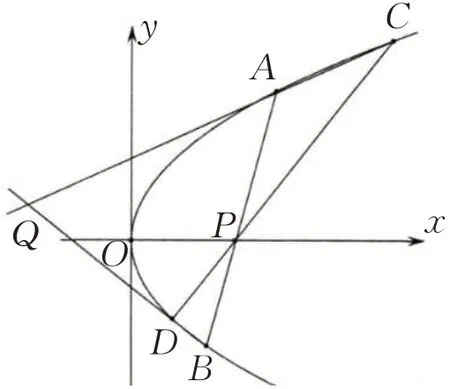
图4

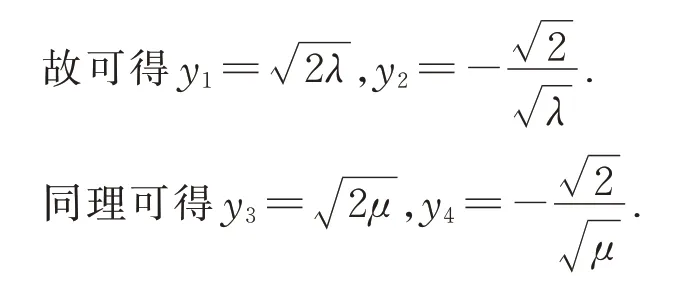
由抛物线两点式方程可得：直线AC:2x=即化简为直线化 简

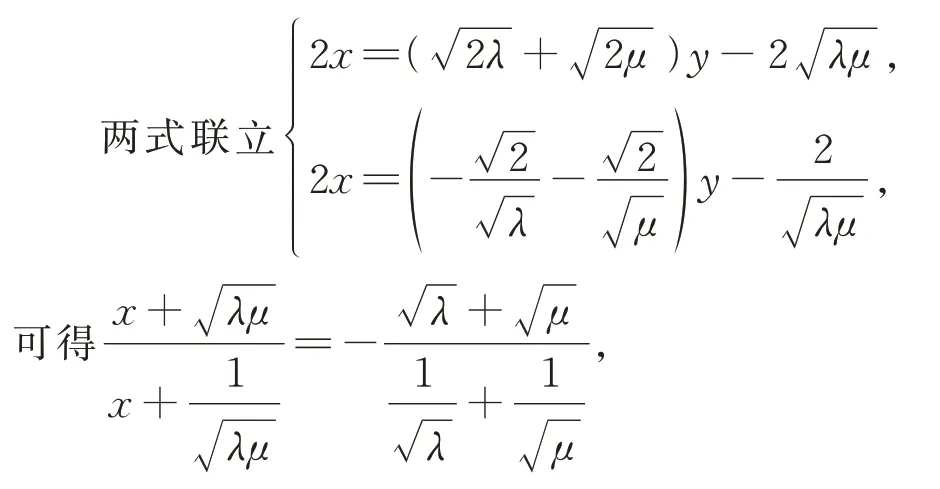
解得x=－1，即点Q在直线x=－1 上．

4 教学启示

如果说试题的解法分析是发散思维，开拓思考的路径，那么试题带来的教学启示就是让思维有发散的源头，让开拓路径的基础更为坚实．

解析几何是高考中的一个难点问题，学生的数学运算能力良莠不齐．许多学生在设参的选择上，没法做出一个合理的选择．本文以点参的角度入手，介绍了定比点差法的原理，思考并归纳了几种常见的适合设点参，利用定比点差法解决的问题，以期帮助学生快速地找到解题的切入点，让学生在解题过程中“有法可依”，让解析几何难题“有迹可循”，能有效弥补部分学生数学运算能力的不足，对广大学生来说是个“福音”．