一道2022 年联考导数题的多视角探究

陕西省西安市临潼区临潼中学 杜 斌 （邮编：710600）

数学家波利亚说过，掌握数学就意味着要善于解题. 纵观近几年新课标高考对导数的考察难度不减，形式却更加灵活. 而导数相关问题犹如中学数学皇冠上一枚璀璨的明珠，此类问题解答对学生的综合解题能力要求较高，有时甚至涉及到高等数学的部分知识. 然而，研究导数相关问题有助于提高学生实践能力和创新意识. 因此，高考导数部分备考教学上加强对一题多解的训练就显得不可或缺.

题目呈现(2022 汉中市高三校际联考理数)已知函数f(x)=xex－mx.

(1)当m=0 时，求f(x)在(t，+∞)上的单调区间;

(2)若f(x) ≥lnx+x+1 对x∈(0， +∞)恒成立，求实数m的取值范围.

解(1)略；第(2)问，如下：

解法1(分离参数、指数同构放缩得范围)

当x+lnx=0 时取等号，数形结合知x=x0(＞0)时，x0+lnx0=0，则h(x)min=0.

所以m≤0，故m的取值范围为：(－∞，0].

点评为求出h(x)min，将xex变为其指数同构式ex+lnx，再利用切线放缩知识，得ex+lnx≥x+lnx+1，得h(x)min=0，可得到m的范围. 运用切线放缩过程中要把握好放缩的大小、方向及等号能否成立.

解法2(分离参数、对数同构放缩得范围)

当xex=1 时取等号，数形结合知x=x0(＞0)时，x0ex0=1，则h(x)min=0，所以m≤0，故m的取值范围为：(－∞，0].

点评受解法一的启发，为了求出h(x)min，将x+lnx变为其对数同构式lnxex，再利用切线放缩知识得xex－1 ≥lnxex得h(x)min=0，同样可得到m的范围.

解法3(半分离、隐零点破难点)

将原问题转化为：mx≤xex－lnx－x－1对x∈(0，+∞)恒成立.

下求g(x)=xex－lnx－x－1 的最小值.

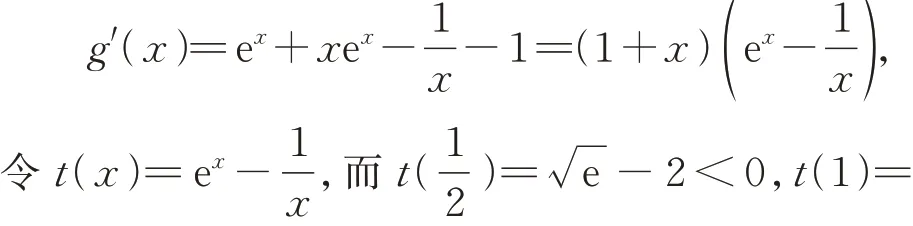
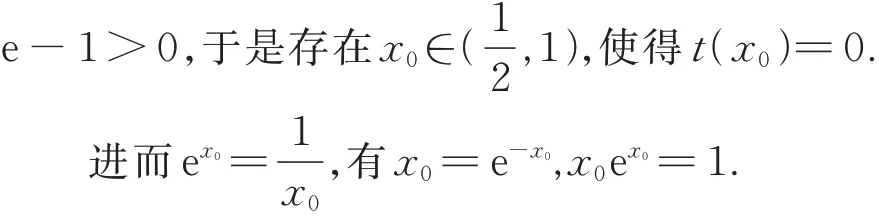
所 以x∈(0，x0)，t(x)＜0， 有g′(x)＜0；x∈(x0，+∞)，t(x)＞0， 有g′(x)＞0，即g(x) 在(0，x0)单调递减，在(x0，+∞)单调递增.

所以g(x)min=g(x0)=x0ex0－lnx0－x0－1=－lnx0－x0=－ln e－x0－x0=0.

注意到x→0，g(x)→+∞，x→+∞，g(x)→+∞，数形结合(图1)， 要mx≤0，有m≤0，故m的取值范围为：(－∞，0].

图1

图2

点评将原问题进行半分离参数，为了求出g(x)min，可求g′(x)=0 的隐零点x0，虚 设代换求得g(x)min. 特别是在含lnx， ex形式导数不等式中隐零点较为常见，应结合题目特点对等式进行相应变形.

结 合 式②，得h(x)min=(1+x0)·0=0，有m≤0，故m的取值范围为：(－∞，0].

点评将问题分离参数后研究h(x)的性质.求h(x)的最小值h(x0)，虽不能准确计算出h(x0)，但可通过二次求导，隐零点代换、构造函数可得h(x)min=0. 此解法较为繁琐，但却蕴含了重要的转化、构造思想.

解法5(凹凸相切、信息技术解疑惑)

以上五种解题策略蕴含着含参导数取值范围问题常见的基本方法和数学思想. 一般分离参数作为含参导数问题首选策略，应考虑到函数具体形式的多样性，适当利用切线放缩可大大减少计算量；若直接对函数性质研究有时要多次求导，同时还要注意结合隐零点虚设代换，这要求学生有较强的逻辑思维能力及数学运算水平；若借助函数凹凸性考虑相切情形，较为简便，特别在选择题、填空压轴题显得较为方便. 在教学中教师不但要关注基本知识技能，更要注重各种解法中渗透的数学思想、方法的积累，关注不同层次学生思维的广度和深度，不断提升学生的综合解题能力.