用问题提出构筑单元思维结构

谢光玲

摘要：为了“减负增效”全面提升小学生的数学素养，在教学实践中，利用学生自主提出的问题，或者教师结合情境提炼而出的问题，不仅能激发学生主动学习的积极性，还能让每一个学生透过浅表的、碎片化的知识点学习，走向对同类知识、关联知识乃至但大单元结构的理解性学习，再利用这样的结构去深入数学学科本质，真正实现数学素养的提升。

关键词：小学数学;问题提出;思维结构

一、问题提出

图形的周长、面积内容的编排从三年级延至六年级，时间跨度长，但这部分内容的问题解决最终都依赖转化思想和空间想象的帮助。因此按照年级层级的顺序，逐步帮助学生建立转化思想和空间想象的思维结构，就是这个版块内容教学的关键抓手。

为了解决以上困惑，扬长避短，以《组合图形的面积》一课的教学实践，用问题提出设疑激趣、让学生经历：打通新旧知识间的壁垒，学会剥离情境的外衣，探究问题解决的本质，反复思辨、普遍联系，构建解决一切问题的观念，形成抽象的思维结构，再结构化地养成稳定的适合自身发展的数学自觉。

二、课堂实践

（一）教学目标

1.通过对组合图形与基本图形的异同的比较，利用二者的关联进行空间想象和数学转化，自主学会解决组合图形面积的计算问题。

2.让学生在组合图形面积问题的解决中，构建主动寻求策略、进行转化的意识，提升学生的问题解决能力。

3.通过问题解决，体会转化思想的价值，感悟数学思维结构化的魅力。

（二）教学重点

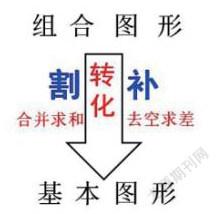
让学生主动利用割、补等转化方法解决组合图形的面积问题。

（三）教学难点

利用空间想象把组合图形转化成已学过的基本图形。

（四）教学过程

1.找不同，提出问题——触摸结构

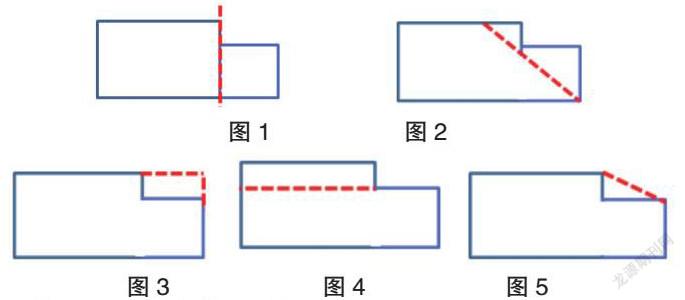
师：仔细观察图形，你发现了什么？有什么疑问？

生：这个图形和以前学过的图形不一样，它叫什么名字？

生：它像长方形的一部分，它是不是长方形被挖去了一块？

生：我觉得它像两个图形拼在一起的，是不是叫拼组图形？

师：你们都发现了这个图形的关键所在，它跟以前学过的图形确实不一样，它叫组合图形，你还发现了哪些新问题？

生：它的周长拉一拉就是大长方形的周长，面积变小了，是多少呢？

师：好问题，这节课我们就来研究组合图形的面积。（板书课题）

设计意图：去情境地直接问题提出，快速地让学生把思维向内提取“象什么”，发现问题，顺其自然把旧知新问用视觉上的“象”勾连到一起，为二者间的互相转化生活基础，无痕化地让学生沉浸到空间想象和空间直观之中，提高课堂效率，为解决本课的重点——组合图形的面积孕伏开启密码。

师：它的面积还能像以前那样用某个公式直接算出来吗？

（稍作思考）

生：虽然不能直接算出来，但是我可以把它变成两个长方形，就是从那里画一条线隔开，就可以算了。

生：对，他说的方法可以求出图形的面积，只要加起来就可以了。

师：好方法！此处应该有掌声。你有一颗会运动思考的智慧大脑。

生：我觉得这个组合图形跟大长方形有关系，它在大大的长方形里。

…….

2.探究新知，解决问题——搭建结构

（1）独立尝试，自主个性化建构

师：想法很多，为什么这样想？把想法变成成果吧！请在作业纸上画一画。

（在作业纸上画图尝试）

设计意图：不急于问题解决，把图形转化与计算分开，让学生有充足的时间勾连基本图形与组合图形问题解决的思维结构，去伪存真让二者建立联系，为思维的结构化提供了广阔的生长空间。

（2）展示交流，合作社会化建构

师：这些方法有什么不同？

生：画线的位置不一样，有的在图形的里面，有的在图形的外面。

师：你很善于比较，请你把这两种方法起个名字。

生：就叫割开和添补吧。（板书）

师：线的位置画的不同，产生的结果一样吗？

生：不一样，线画在外面的，都多围了一块面积进去，还要去掉，线画在图形内部，是把图形分开成几个图形的，只要加起来就可以求出面积了。

师：这么多的方法都能计算出面积吗？请拿出作业纸，用多种方法想一想、试一试、算一算。

（3）多维思辨——垂直化建构

师：仔细观察这些计算过程，你又发现了什么？

生：方法都不一样，有的用加法、有的用减法。

師：用加法的有什么共同点？减法呢？

生：我发现了用分割法转化的都用加法计算的，添补转化的都是用减法计算的。

师：对比分类，发现规律，热烈掌声送给这位善于概括总结的同学。因为需要解决的是这个组合图形的面积，因此当添补时要去空求差，分割时要合并求和。（板书）

（4）反思质疑，活化建构

师：对于用转化的方法求组合图形的面积，你觉得应该注意些什么？你有什么感受？

“我突然发现一个有趣的现象，我眼睛里虽然看见的是组合图形，但看着看着就发现这些图形变了，变成一个个我已经学过的图形了，特别简单，一下子就算出来了。”“你说的还不够准确，变成规则图形也不一定就能算出来面积。”“只要是规则的就可以用公式算，不过这个规则图形要是我们已经学过的。”“我也不同意你的观点，我画给你看，这个样子你还能算出面积来吗？”

（全班惊叹）

“所以，还要在他想法的基础上加个条件，数据够用才可以。”（上台补充板书）

（全班鼓掌）

“我结合自己和别人的解法发现：用割的方法，面积都没有变大，还在原图形内所以都用加法;补的时候，原图的面积变大了，所以要用减法。”

“确实，割的时候要合并求和，补的时候要去空求差，我老爸说的。”

“你说的是简单的问题，还有的题会把两种方法都用上，这时加法、减法都会用到。”

师：你能举个例子，让同学们看看吗？

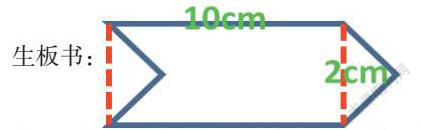
生板书：

师：这个问题特别好，请各自尝试能否解答出来。

（生口答即可）

3.数形结合，延展提升——拓实结构

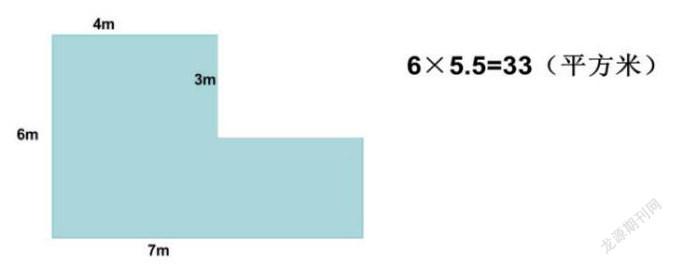
师：对于这个组合图形，有人列出了这样的算式，你知道是怎么转化的吗？

设计意图：此题是教材中主情境问题，是一个有特殊解法、且是学生已经“会了”的，那么会到什么程度？反其道出示，让学生由数想形，既能考察学生“会”的程度，让学生由形算数再到有数想形，锻炼、培养学生的空间想象能力，拓实、牢固思维结构。

（学生先思考，再做尝试）

生1：我看见6×5.5就想到长方形的面积，于是我就想办法把这个图形转化为长方形，但是式子中没有加也没有减，所有单一的割、补都不行的，那么就试试又割又补，再看着数据6，没变，7和4要变成5.5，我就想到从多出来的那一块竖着从中间割开，而割下来的宽正好是3，正好补到上面就可以了，我再验证一下，确实是对的！

（全班掌声）

生2：其实我想到的比他的复杂一点，想象成梯形，割下三角形再补上去，但是算式要变一下形，这道题好有意思哦。

……

4.反思创新——延展结构

师：在一个又一个的问题解决中，你最深的感受是什么？

生1：我感受到图形在运动，规则、不规则可以互相转化、复杂、简单之间也能互相转化。

生2：我最深的感受是思考问题要全面，有序。

师：有故事哦，请你说说为什么有此感受。

生2：第二个问题，我没有想到还有那样的解法，割、补可以分开用，也可以同時用，因为我没有看到图中数据的特殊，就没想到同学们那种“美妙”的方法。太神奇了！

生3：我感受最深的是，学无止境。这节课我已经学过了，结果还是有这么多问题我没有思考到，以后要更加虚心了。

教师布置作业：请你设计一个能用3.14×9计算的面积的组合图形。

设计意图：完全地由数想形，给学生无限空间想象空间，可以是线段围城的组合图形，可以是半径为3的圆拆组的图形，让学生由解题者变成命题者，把组合图形的问题解决的策略、方法等一系列的思维构建成一个体系，形成能举一反三的数学能力和稳定的大结构。

三、研究结论

（一）自主提问，给学生自主触摸单元结构的机会

问题是数学的心脏，能提出好问题，正是学生具备数学素养的重要表现。本节课，用“找不同，提问题”这一学生数学的小游戏，让学生必须把新问题与旧知在反复对比中建立联系，触摸到隐藏在这个图形背后组合图形与基本图形的联系与区别，方可提出核心问题：这个图形像什么、是什么、怎么解、为什么这样解、还能怎么解，一系列问题的解决也就顺势让学生主动地参与到建立思维结构-拓实思维结构-思维的结构化的过程之中，既调动了学生积极参与学习的主动性，又兼顾了每个学生可以有差异地解决问题、感知、体验数学思想、方法的全过程，为数学素养的提升提供坚实的基础。

（二）重视体验，感悟单元思维结构化的应用价值

建立结构、搭建模型是数学问题解决常用的教学手段，但建立的“小结构”能否生长，持续助推数学核心素养的发展和提升，还需要重视体验，还需要思维结构化的引领和牵动。课末，让学生自主设计满足算式的组合图形，不仅要求学生拥有对算式的几何直观能力，还要掌握割、补转化方法的精髓——什么图形转化成什么图形。数形能够自由行走，正是学生的空间想象和空间观念素养发展和提升的直接体现，也是建立的思维结构在无限延申的重要标志。

参考文献：

[1] 关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见，中共中央办公厅、国务院办公厅印发，2021年7月24日.

[2] 义务教育数学课程标准（2022年版）[M].北京：北京师范大学出版社，2022.

[3]魏建宾.小学数学课堂中如何有效地渗透德育教育探究[J].文理导航（下旬），2021（09）：35-36.

本文系安徽省电教馆2020年规划课题《智慧环境下集体备课单元教学的实践研究》（课题编号：AH2020128）研究成果之一。